高速铁路CRTSⅡ型板式轨道高低不平顺敏感波长的分布特征及影响因素*

王有能 徐金辉 孙劲松 冯青松 王永华

(1.中国铁路上海局集团有限公司上海工务段,200071,上海;2.华东交通大学铁路环境振动与噪声教育部工程研究中心,330013,南昌;3.中国铁路上海局集团有限公司工务部,200071,上海∥第一作者,高级工程师)

轨道不平顺作为车辆、轨道结构振动的主要激励源,是铁路养护维修的重点内容[1-2]。轨道不平顺波长从几毫米到几百米不等,在众多波长中,有些波长对车辆系统振动有较大的影响,有些波长的影响则较小。我国学者对于轨道不平顺敏感波长开展了大量研究,其中:文献[3-4]将轨道不平顺简化成等幅值、波长递增的谐波,研究了对车辆系统振动有较大影响的轨道不平顺敏感波长;文献[5]利用耦合系统的频域传递特性来研究轨道不平顺敏感波长;文献[6]采用高频轮轨模型,计算不同速度下不同参数的轨道短波不平顺引起的轮轨力,分析了车辆振动与轨道短波不平顺敏感波长之间的关系;文献[7]采用有轨电车车辆-轨道耦合模型,对影响列车运行安全的轨道不平顺敏感波长进行了研究;文献[8-9]利用轨道不平顺与车辆系统动力学指标之间的幅频特性对轨道不平顺敏感波长进行了研究。综上可知,已有研究主要是从车辆系统振动控制的角度研究轨道不平顺敏感波长,其研究成果主要用于保障列车运行的安全、平稳。

与上述研究的侧重点不同,本文以CRTS Ⅱ型板式轨道作为分析对象,从轨道结构振动控制的角度开展轨道不平顺敏感波长的研究,以期降低轨道结构振动,延长轨道结构寿命。为此,本文以轨道的高低不平顺为例,依据轨道不平顺与CRTS Ⅱ型板式轨道之间的振动传递关系,定义了影响轨道结构振动的敏感波长。利用车辆-CRTS Ⅱ型板式轨道耦合动力学模型,计算得到轨道不平顺敏感波长,分析CRTS Ⅱ型板式轨道不平顺敏感波长的分布规律,探讨轨道结构各参数对敏感波长的影响。

1 车辆-CRTSⅡ型板式轨道耦合系统动力学算法

车辆-CRTS Ⅱ型板式轨道耦合系统由车辆系统和CRTS Ⅱ型板式轨道结构组合而成,二者利用轮轨相互作用连接。本文的动力学模型、算法等均采用参考文献[10]的研究结论,选用的车辆-CRTSⅡ型板式轨道耦合系统动力学模型如图1所示。该模型将车辆系统视为多刚体系统,利用哈密尔顿原理建立车辆系统运动方程;将CRTS Ⅱ型板式轨道视为周期结构,建立了每个周期子结构的运动方程,再利用传递矩阵法计算振动波在各子结构之间的传播速度,得到CRTS Ⅱ型板式轨道运动方程;最后利用轮轨相互作用关系,组建车辆-CRTS Ⅱ型板式轨道耦合系统的运动方程。文献[10]已证明了该方法的正确性,本文不再赘述。

图1 车辆-CRTSⅡ型板式轨道耦合系统动力学模型

车辆系统的频域运动方程为:

(-ω2mv+iωCv+Kv)uv=Pv

(1)

式中:

mv——车辆系统的质量矩阵;

Cv——车辆系统的阻尼矩阵;

Kv——车辆系统的刚度矩阵;

uv——车辆系统的位移列阵;

Pv——外荷载列阵;

i——虚数单位;

ω——时间域频率。

轨道子结构的频域运动方程为:

(-ω2mst+iωCst+Kst)ust=Pst

(2)

式中:

mst——轨道子结构的质量矩阵;

Cst——轨道子结构的阻尼矩阵;

Kst——轨道子结构的刚度矩阵;

ust——轨道子结构的位移列阵;

Pst——轨道子结构的荷载列阵。

根据周期结构的特性,利用传递矩阵法可得到轨道结构的运动方程:

Ktut=TtfPt

(3)

式中:

Kt——轨道受力子结构的动刚度矩阵;

ut——轨道受力子结构的位移列阵;

Ttf——轨道受力子结构的荷载转换矩阵;

Pt——轨道受力子结构的外荷载列阵。

车辆-CRTSⅡ型板式轨道耦合系统的运动方程为:

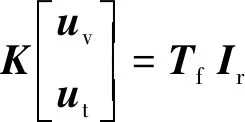
(4)

式中:

K——车辆-CRTSⅡ型板式轨道耦合系统的总动刚度矩阵;

Tf——车辆-CRTSⅡ型板式轨道耦合系统的荷载转换系数矩阵;

Ir——输入的激励(即轨道不平顺)矩阵。

2 CRTSⅡ型板式无砟轨道高低不平顺敏感波长的分布特征

2.1 敏感波长的定义

参考文献[8-9],将能够使CRTS Ⅱ型板式轨道产生较大振动的波长定义为敏感波长。另外,根据幅频特性曲线的定义,也可将幅频特性曲线峰值所对应的波长定义为敏感波长,即主振频率对应的波长。本文中的敏感波长包含了上述两部分范畴。

2.2 敏感波长的分布特征

为便于描述,将第i阶主振频率对应的敏感波长称为第i阶敏感波长。设H(f)为轨道不平顺与CRTS Ⅱ型板式轨道的振动加速度的频响函数(即加速度与波长的比值),则在高低不平顺激励下,CRTS Ⅱ 型板式无砟轨道的幅频特性曲线如图2所示。

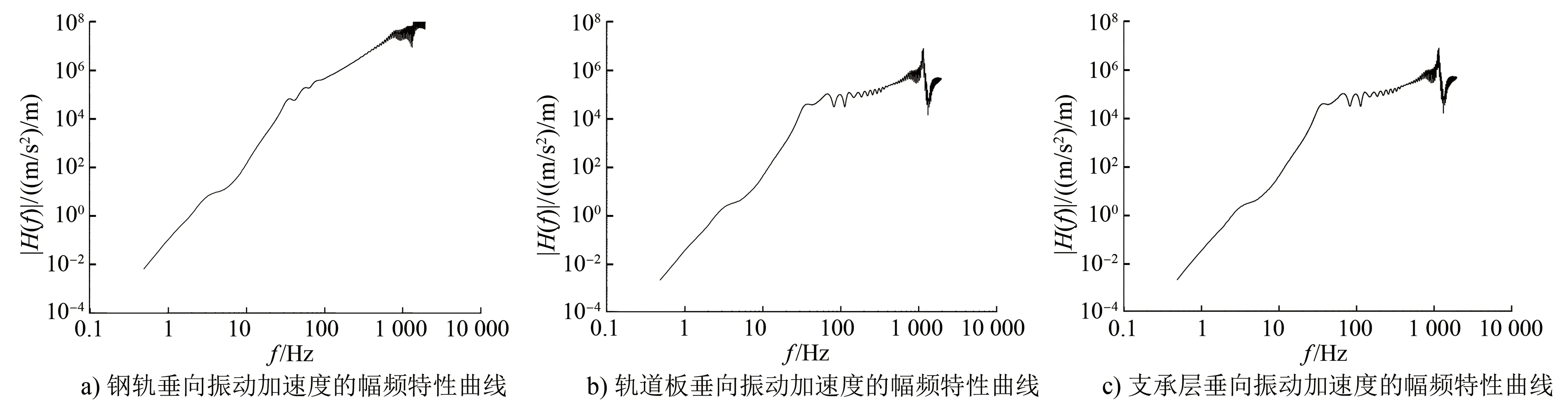
图2 CRTSⅡ型板式无砟轨道的幅频特性曲线

CRTSⅡ型板式无砟轨道高低不平顺敏感波长随阶数变化曲线如图3所示。由图3可知:CRTSⅡ型板式无砟轨道(钢轨、轨道板及支承层)的敏感波长大多集中于中波和短波范围(波长≤5.00 m);轨道板振动加速度与支承层振动加速度的敏感波长基本相同;钢轨振动加速度的前2阶敏感波长(2.72 m及1.69 m)略大于轨道板、支承层振动加速度的敏感波长(2.59 m及1.43 m);钢轨振动加速度的第3阶及以上阶数的敏感波长均小于0.30 m,且小于轨道板、支承层振动加速度的第3阶及以上阶数的敏感波长;轨道板、支承层振动加速度的敏感波长呈指数式分布,第6阶及以上阶数的敏感波长趋于平缓(波长均小于0.50 m)。

图3 CRTSⅡ型板式轨道高低不平顺敏感波长随阶数变化曲线

为便于工务维修部门制定更具针对性的维修计划,本文统计了CRTSⅡ型板式轨道各部位振动加速度的低阶(前5阶)敏感波长,如表1所示。

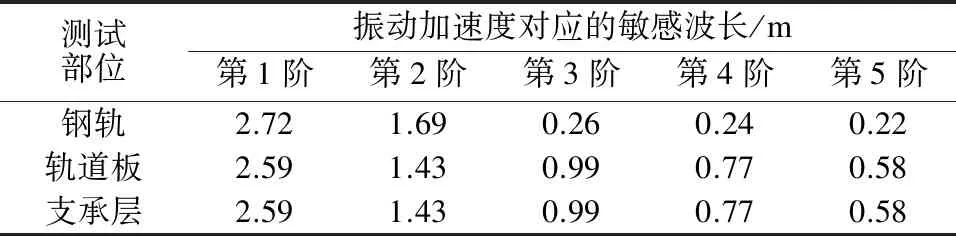
表1 CRTSⅡ型板式轨道振动加速度的低阶敏感波长

3 CRTSⅡ型板式无砟轨道高低不平顺敏感波长的影响因素分析

随着轨道线路的长期运营,轨道结构各参数会产生劣化现象,进而影响其敏感波长。另有研究表明,列车的运行速度对车辆-CRTS Ⅱ 型板式轨道耦合系统的振动有较大影响[3]。因此,本文分析了列车运行速度,以及扣件、CA(水泥沥青)砂浆、路基等在不同计算参数下,轨道不平顺敏感波长的变化规律。根据计算结果可知,各种计算工况下,轨道板、支承层振动加速度的敏感波长基本相同,因此本文仅列出钢轨振动加速度及轨道板振动加速度的敏感波长。

3.1 列车运行速度的影响

分别取列车运行速度v为150 km/h、200 km/h、250 km/h、300 km/h及350 km/h共5种工况进行分析。图4为不同v下的轨道高低不平顺敏感波长分布及前2阶敏感波长随v的变化规律。

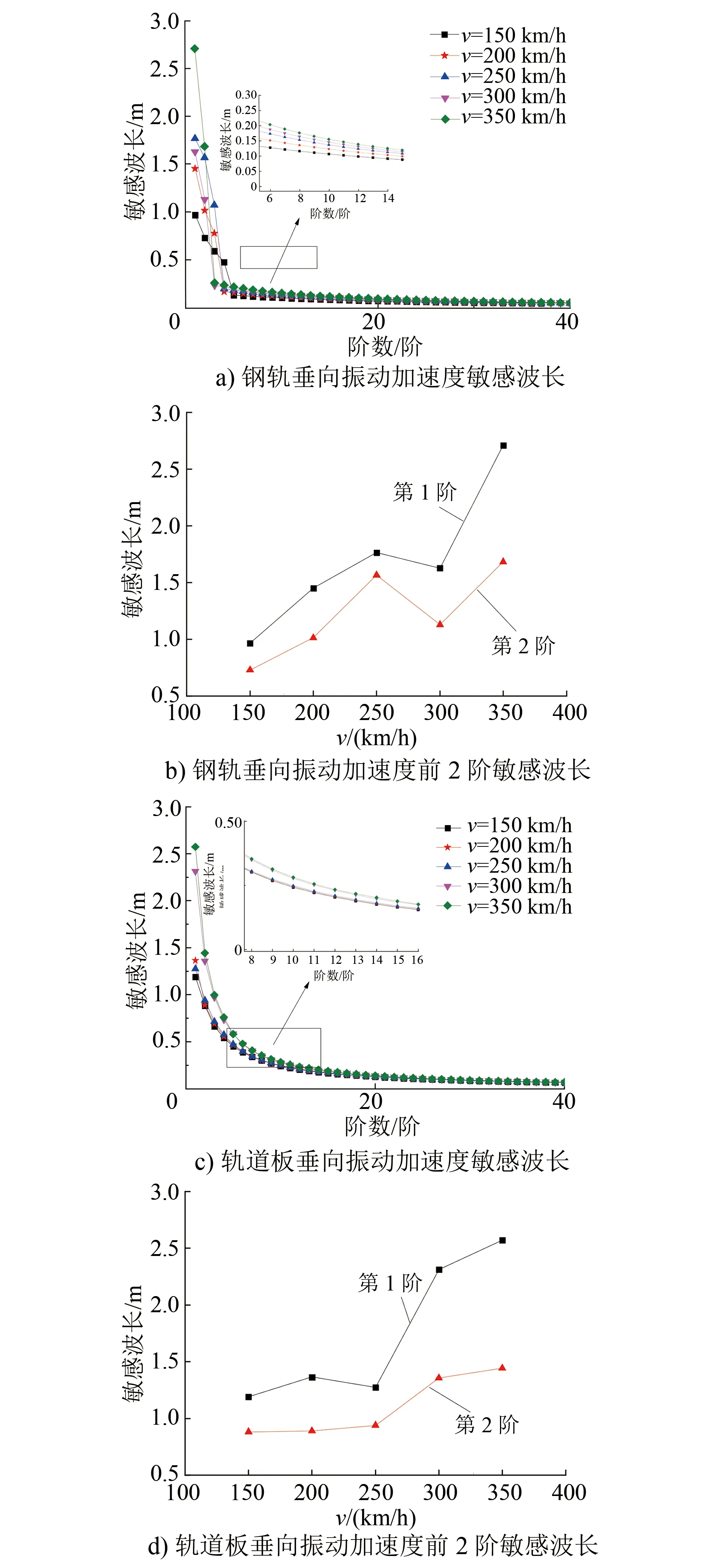
图4 不同列车运行速度对轨道高低不平顺敏感波长的影响

由图4可知:随着v的增大,轨道高低不平顺敏感波长整体呈增大趋势,但并不是严格的单调变化。如图4 b)所示,当v由150 km/h增至250 km/h时,钢轨振动加速度第1阶敏感波长随之增大,但当v增至300 km/h时敏感波长有所减小,当v增至350 km/h时敏感波长又开始增大。究其原因,主要是随着v的增大,CRTSⅡ型板式轨道的幅频特性曲线会出现“频移现象”。根据波长的定义可知,当v增幅大于频移幅度时,敏感波长会增大,反之则减小。另外,各项动力学指标的高阶敏感波长(均为短波)随v增大而增大,与钢轨垂向振动加速度敏感波长增幅较大相比,轨道板、支承层垂向振动加速度敏感波长的增幅相对较小。

3.2 扣件的影响

在线路长期运营过程中,轨道下方的胶垫会产生老化现象,导致扣件刚度及扣件阻尼发生变化,进而影响其敏感波长。本文选取扣件垂向刚度及扣件垂向阻尼2个参数,用以分析不同扣件参数取值对敏感波长的影响。

扣件垂向刚度对轨道高低不平顺敏感波长的影响如图5所示。由图5可知:扣件垂向刚度对轨道高低不平顺的前3阶敏感波长有一定影响,但对第4阶及以上阶数的敏感波长基本无影响。

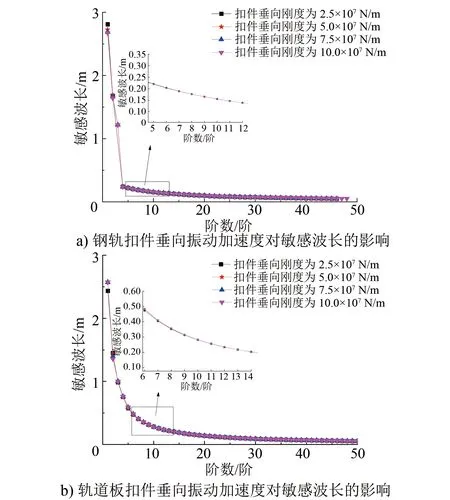
图5 扣件垂向刚度对轨道高低不平顺敏感波长的影响

轨道高低不平顺低阶敏感波长随扣件垂向刚度的变化如图6所示。由图6可知:钢轨垂向振动加速度前2阶敏感波长随扣件垂向刚度的增大而略有减小,第3阶及以上阶数的敏感波长则无明显变化;当扣件垂向刚度由2.5×107N/m增至5.0×107N/m时,轨道板垂向振动加速度第1阶敏感波长明显增大,第2阶及以上敏感波长保持不变;轨道板垂向振动加速度的第2阶敏感波长随扣件垂向刚度的增大而略有减小,第3阶—第5阶敏感波长则略有增大,但增幅较小。

轨道高低不平顺低阶敏感波长随扣件垂向阻尼的变化规律如图7所示。由图7可知:钢轨垂向振动加速度低阶敏感波长均随扣件垂向阻尼的增大而略有减小,其中,前2阶敏感波长的降幅稍大,其他各阶敏感波长的降幅很小。随着扣件垂向阻尼的增大,轨道板垂向振动加速度的各阶敏感波长基本保持不变。

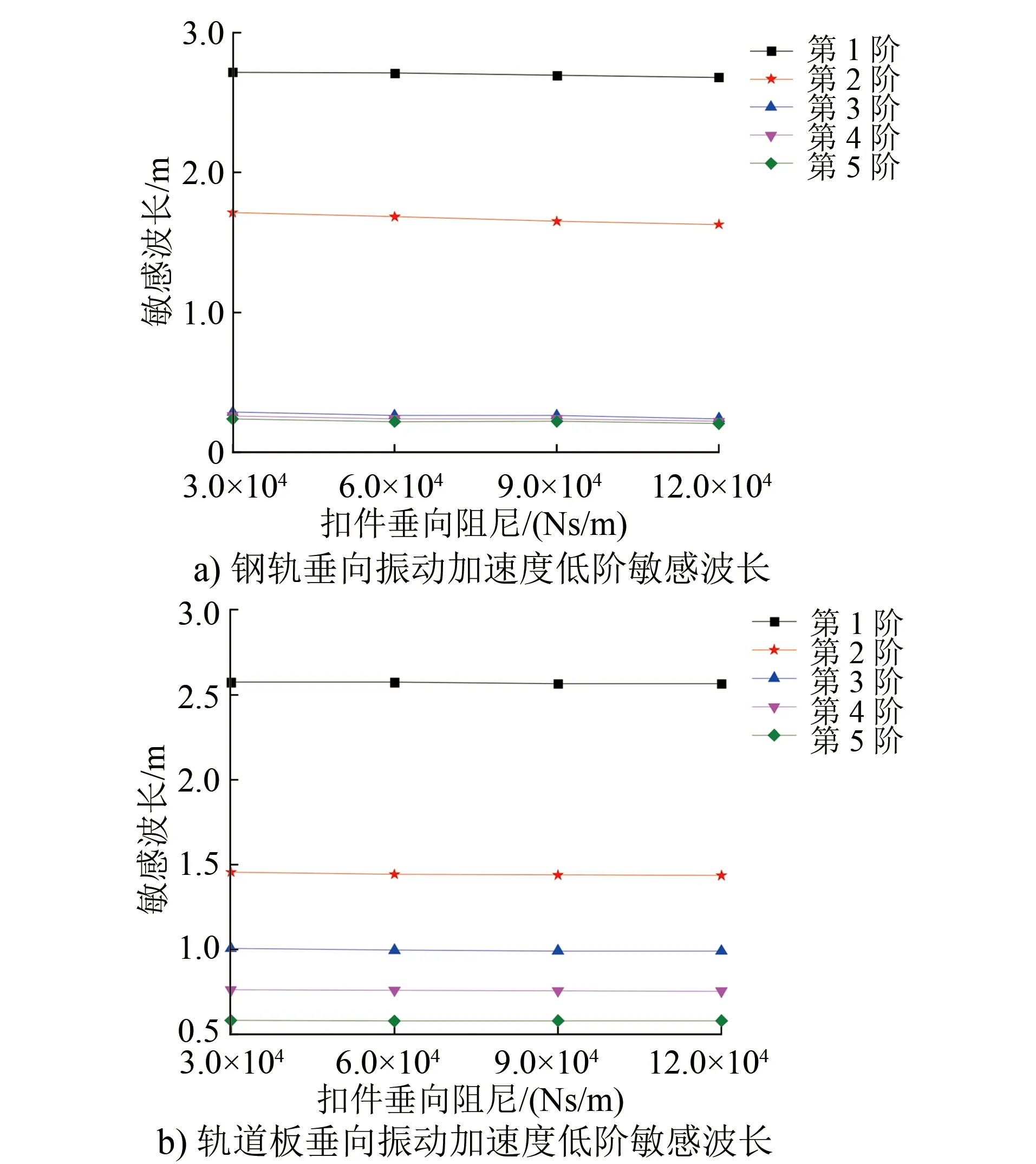
图7 轨道高低不平顺低阶敏感波长随扣件垂向阻尼的变化

3.3 CA砂浆的影响

CA砂浆作为一种填充材料,除可承受一定荷载外,还可填充轨道板与底座的空隙,以保证列车平稳运行。本文选取了4种不同的CA砂浆工况(其计算参数见表2),分析CA砂浆弹性模量和垂向阻尼不同取值对敏感波长的影响。

表2 不同CA砂浆工况的计算参数

通过对比发现,不同CA砂浆工况对钢轨、轨道板垂向振动加速度低阶敏感波长的影响非常小,为此,本文不再逐一罗列低阶敏感波长随这2个参数的变化规律。

3.4 路基的影响

高速铁路无砟轨道对路基变形的要求十分严格,路基参数取值对车辆-轨道耦合振动有较大影响。本文选取路基垂向刚度和路基垂向阻尼2个参数,用以分析不同参数取值下对敏感波长的影响。

轨道高低不平顺低阶敏感波长随路基垂向刚度的变化规律如图8所示。由图8可知:钢轨垂向振动加速度的前2阶敏感波长随路基垂向刚度的增大而减小,第3阶及以上阶数的敏感波长基本保持不变;当路基垂向刚度由3.5×107N/m增至7.0×107N/m时,轨道板垂向振动加速度的第1阶敏感波长明显增大,随后敏感波长随路基垂向刚度的增大而保持不变;轨道板垂向振动加速度的第2阶敏感波长随扣件垂向刚度的增大而减小,第3阶及以上阶数的敏感波长则变化较小。

图8 轨道高低不平顺低阶敏感波长随路基垂向刚度的变化

轨道高低不平顺低阶敏感波长随路基垂向阻尼的变化规律如图9所示。

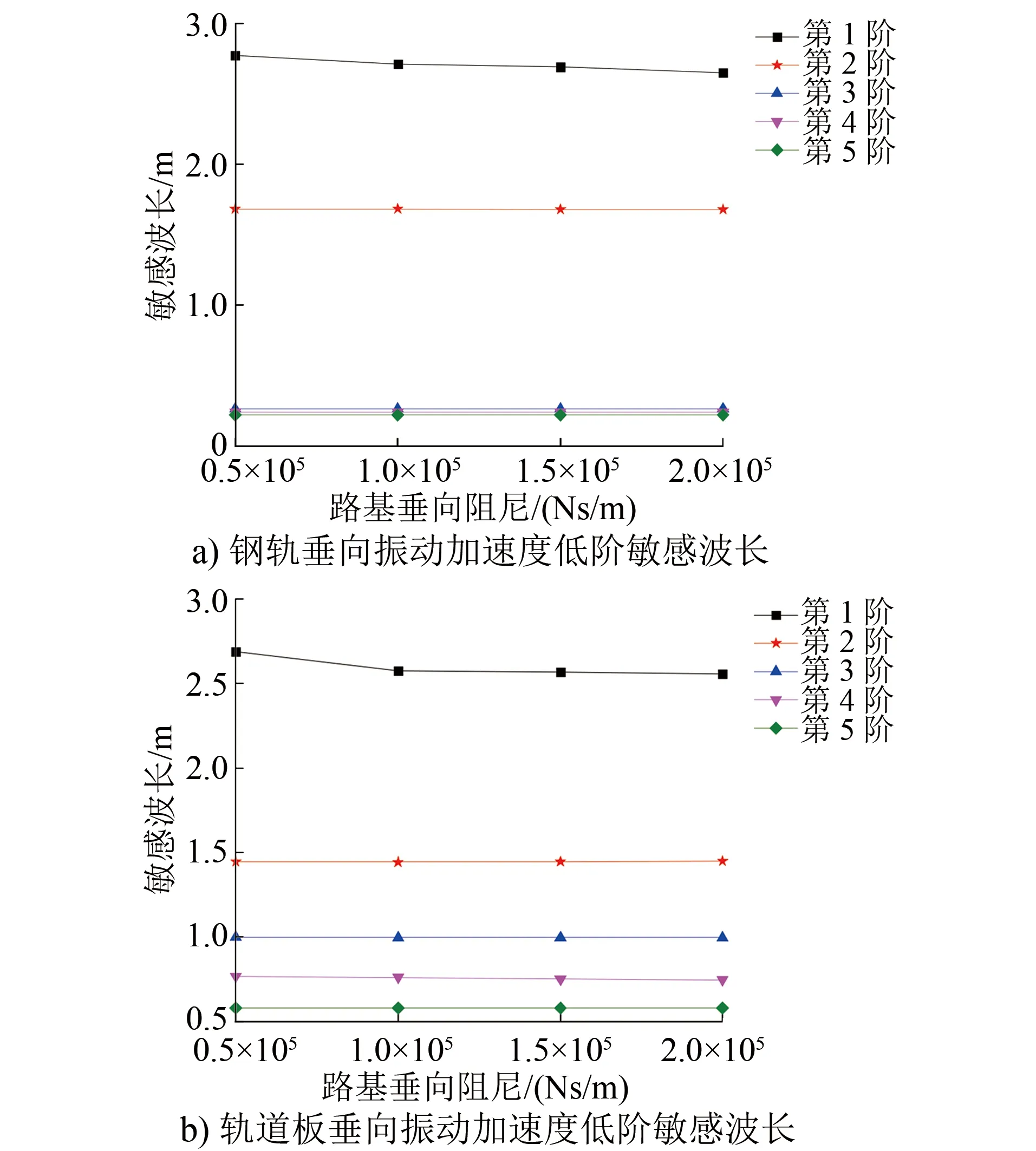
图9 轨道高低不平顺低阶敏感波长随路基垂向阻尼的变化

由图9可知:钢轨垂向振动加速度的第1阶敏感波长随路基垂向阻尼的增大而减小,第2阶及以上阶数的敏感波长基本保持不变;轨道板垂向振动加速度的第1阶敏感波长随路基垂向阻尼的增大而减小,第2阶及以上阶数的敏感波长变化较小。

4 结语

本文依据轨道不平顺与CRTSⅡ型板式无砟轨道振动之间的幅频特性曲线,分析了轨道高低不平顺敏感波长的分布特征,探讨了列车运行速度及轨道结构各参数对敏感波长的影响。本文的研究结果可为CRTSⅡ型板式无砟轨道的振动控制及维护提供依据。研究结果表明:

1) 影响CRTSⅡ型板式无砟轨道振动的敏感波长均集中于中、短波范围内(波长≤5.00 m)。钢轨振动加速度的敏感波长与轨道板、支承层振动加速度敏感波长存在较大差异,而轨道板振动加速度的敏感波长与支承层的敏感波长相近。此外,低阶敏感波长的分布较为松散,高阶敏感波长的分布则较为密集。

2) 从整体趋势上看,轨道高低不平顺敏感波长呈现出随列车运行速度增大而增大的现象,但并不是严格的单调变化,某些指标的敏感波长会交替出现增大与减小的现象。另外,各项动力学指标的高阶敏感波长(均为短波)随列车运行速度增大而增大;钢轨垂向振动加速度的敏感波长增幅较大,轨道板、支承层垂向振动加速度敏感波长的增幅相对较小。

3) 扣件系统各参数主要影响低阶敏感波长(尤其是前2阶敏感波长),对高阶敏感波长的影响较小;扣件垂向刚度对敏感波长的影响相对较大,扣件垂向阻尼对敏感波长的影响则较小。

4) CA砂浆各参数对各项轨道不平顺敏感波长几乎无影响。

5) 路基各参数主要影响低阶敏感波长(尤其是前2阶敏感波长),对高阶敏感波长的影响较小。