劳动生产率与最优假日配置——模型、仿真与实证

魏 翔

内容提要：本文基于时间配置理论建立公共假日的混合整数非线性规则(NMIP)动态治理模型,利用求解约束整数程序(SCIP)算法器进行仿真测算,并利用126个经济体的数据进行实证检验。研究结果表明,分散休假模式既有利于劳动生产率最大化又有利于长期增长,是能够促进经济高质量发展的最优假日治理模式。因此,可以考虑对当前的黄金周等行政性集中休假制度进行适当调整,提高公共假日在全年分布的分散性,增强节假日安排的固定性和制度性,并通过推进带薪休假和短假期的自主结合来满足人们探亲访友、长途旅游的需求。

一、问题提出

假日制度是国家政治、经济、文化制度的重要反映,涉及经济社会的多个方面,也关系着广大人民群众的切身利益。国际通行的公共假日模式是制度性分散休假模式,即政府不进行全国性的行政调控、人为地挪动公共假日,而是保持每个假日在日历时间上的制度性稳定。中国的假日制定经历了从侧重劳动保障、力图提振内需到追求高质量发展的过程。在强调促进消费的时期中,黄金周作为一项积极的假日治理政策应运而生。这是一项具有中国特色的政策创新,通过挪假的方式来促进消费、提振内需,进而刺激经济增长。但是,在人们迫切希望提高假日体验质量的需求下,集中休假制度引发了旷日持久的争论,即在高质量发展阶段,以黄金周为代表的行政性集中休假制度是否有利于进一步提高生产率与经济发展质量?

在黄金周出台之前,中国从每周一天休假逐渐增加到每周双休[1]。1999年,国务院发布的《全国年节及纪念日放假办法》首次推出黄金周以扩大内需;2000年,《国务院办公厅转发国家旅游局等部门关于进一步发展假日旅游若干意见的通知》(国办发〔2000〕46号)明确每年通过调休安排出春节、“五一”和“十一”三个黄金周假期。在这些政策的推动下,假日经济迅速发展,居民的消费潜能得到较大的释放[2-4]。杜江和张倩(2001)通过建立消费支出和闲暇时间选择模型,证实了假日经济对扩大消费需求的作用[5]。近年来,行政性集中休假加剧供需矛盾、降低体验质量等问题凸显[6-7];黄金周集中休假模式只有水平效应,在增加旅游休闲消费的同时却挤出了其他方面的消费,对经济增长作用有限[8-9]。随后,集中的行政性休假制度于2007年进行了调整:取消“五一”黄金周,增加传统节假日(1)2007年,《国务院关于修改〈全国年节及纪念日放假办法〉的决定》将“五一”国际劳动节调整为1天,并增加清明节、端午节和中秋节各1天的传统节日假期。执行时挪动假日附近的周休日最终形成“两大(国庆、春节)五小(元旦、清明节、劳动节、端午节、中秋节)”的新黄金周假日格局。。然而,此次调整对经济增长和消费增长的宏观改善依然不明显,集中休假的模式很可能难以消除消费陷阱[10]。

假日治理的目标应和本国的国情和发展目标相一致。中国正在从高速发展向高质量发展进发,中国经济增长更需要依靠劳动生产率的提高[11]。从长期目标来看,公共假日的科学配置应着眼于劳动生产率优化[12],赋能高质量发展。

劳动经济学的工作-闲暇选择模型证明了工作日和休假日的合理配置能显著改善劳动生产率。对此,跨学科研究进一步揭示工作-休息循环中的两种效应:一是抗疲劳效应(effects of fatigue),即工人们的精力在休息日得以恢复[13-14];二是经验效应(effects of experience),即连续工作能持续积累并提升知识或经验,提高劳动生产率,这也被称为“干中学”效应或知识累积效应[15-16]。此时,劳动生产率依赖于工作的存量[17]。通常认为在工业化阶段,假日配置的经验效应更显著,劳动生产率随着工时的增加而提高[18-19];但在进入工业化后期或进入后工业化社会后,抗疲劳效应更为明显,劳动生产率随着工作时间的增加而递减[20]。这说明劳动生产率和工时之间是非线性的关系[21-22]。因此,工作时间和假日时间都不宜过长[23-24]。进入后工业化社会,假日总量通常存在调整刚性,要想进一步提高生产率,应更加关注公共假日的结构调整而非总量变化[14,25],因为不同的国民休假时间表会导致劳动生产率的差异。因此,对公共假日的结构化改革不仅关乎国民的休息福利、就业和消费,还能有效作用于劳动生产率,促进高质量发展。

然而,国内对假日治理的理论建模和量化分析还处在初级阶段,尤其缺乏以劳动生产率为最优化目标的长期性分析。与以往研究相比,本文的主要创新点在于:(1)在理论上,探索性地构建最优假日治理模型,在劳动生产率框架下捕捉假日配置的动态过程,实现离散动态的仿真测算,证明分散式休假制度是效率最优的假日治理模式;(2)在方法上,调用求解约束整数程序(SCIP)算法器,利用最优求解工具箱(OPTI toolbox)获取假日配置的离散动态最优解;(3)在实践上,为推进假日改革、助力“稳增长”政策、推动高质量发展提供参考。

二、假日治理模型

(一)模型设置

公共假日配置可分为行政性集中休假模式和制度性分散休假模式。前者如中国的黄金周,通过政府挪假形成连续假期;或由企业主导的带薪休假,如欧洲的圣诞节长假和日本的五月黄金周假期。后者则为制度刚性配置,法定节假日按原始制度分散于年内。因此,高质量发展框架下的假日治理模式选择应以劳动生产率优化为准则。其微观基础在于,在厂商进行利润最大化生产的过程中,遇到节假日时机器设备等资本投入在短期内无法迅速调整,只有劳动力要素可以进行调整,而调整的准则就是实现劳动生产率最大化[25]。由此,建立内生劳动生产率的最优假日治理模型。

个体在第t天的劳动生产率Lt是其在工作时间内的有效劳动,由精力Vt和工作经验Et决定,即:

(1)

其中,αv∈(0,1) 是精力Vt对劳动生产率Lt的弹性。在休假日中,人们的疲劳得到缓解、产生精力或活力,因此假日对劳动生产率具有抗疲劳效应,αv即抗疲劳效应的强度[25]。αe∈(0,1)是经验Et对劳动生产率的弹性。在工作日中,连续工作能经由“干中学”效应积累工作经验,因此工作日对劳动生产率具有经验效应,αe体现了经验效应的强度[17]。

精力Vt在工作日中不断损耗,这种损耗具有累积性,按损耗率δv贬值[14]。Vt在休假日内得以恢复,但不受之前精力水平的影响,按固定量εv增加[26]。于是,精力Vt的动态积累路径为:

Vt+1=(1-ut)(1-δv)Vt+utεv

(2)

工作经验Et在休假日不断损耗,这种损耗具有累积性[27-30]。这是因为,不工作的时间越长,人们对经验、知识的遗忘就越快,人力资本贬值就越多[29-30],当人们再回到工作中时,就越难“捡回”(retrieve)原来的经验或知识[28]。同时,新经验的增加建立在原有经验的基础上,具有累积效应[15-16,31],设其累积率为εE。于是,Et的积累路径为:

Et+1=ut(1-δE)Et+(1-ut)(1+εE)Et

(3)

其中,工作经验损耗率δE∈(0,1]。在极端情况下(如超长的产假或长时间的失业),个体的经验或知识会遗忘殆尽(δE=1),以至于既有的经验损耗到零,出现工作失能(Et+1=0)。经验积累率εE∈(0,+∞),代表“干中学”的程度。

人们在工作时,工作经验日增但精力日减,于是需要休息;在休假时,精力不断恢复但工作经验却日减,于是需要继续工作。因此,在工作-休假循环中存在劳动生产率的非线性权衡(non-linear trade-off):由于存在抗疲劳效应,并不是工作越多,劳动生产率越高;由于存在经验效应,也不是休假越多,劳动生产率越高。于是,存在最优假日配置的动态最优化问题:

(4)

s.t.Vt+1-Vt=[(1-ut)(1-δv)-1]Vt+utεv

(4.1)

Et+1-Et=[ut(1-δE)+(1-ut)(1+εE)-1]Et

(4.2)

(4.3)

Vt=0=V0

(4.4)

Et=0=E0

(4.5)

(二)稳定性分析

为求解式(4)的动态最优化问题,需要进行稳定性分析。与传统动态系统的常变量序列[32-33]不同,式(4)存在时变变量ut,其稳定性判别涉及复杂的范数估计式[34-35]。为了回避这种复杂性,此处用断点讨论的方法来判别稳态解的存在性和唯一性。

精力Vt的动态约束路径式(4.1)存在均衡解:

(5)

图1 精力Vt的两个稳定点

式(5)是一条依存于ut的离散时间路径,依存于两个断点ut=0(工作日)和ut=1(休息日),进而存在两个均衡点(V*,u)=(0,0)和(V*,u)=(εv,1)。无论ut如何取值,都存在|(1-ut)(1-δv)|<1,所以这两个均衡点都是稳定点(图1)。但是从经济意义而言,稳定点(V*,u)=(0,0)是一个极端点,表示在长期中连续工作时间过长所导致的“过劳死”(V*=0)。因此,更具普遍意义的稳定点是(V*,u)=(0,εv),即长期中个体的精力在休假中得以不断涵养,最终稳定于休假质量的边际量εv上。

图2 工作经验Et的一个稳定点和一个发散点

综上,动态系统存在唯一的稳定点,即Vt和Et的稳定点都落在休假期间。这说明人们在高质量的假期中获得最高程度的精力恢复。

(三)最优解的动态求解框架

式(4)的汉密尔顿(Hamilton)函数为:

(6)

满足劳动生产率Lt最大化的庞德里亚金(Pontryagain)条件为:

λT=ρT=0

V(t=0)=V0

E(t=0)=E0

当t为休假日时ut=1,有:

Vt+1-Vt=-Vt+εv,即Vt+1=εv

Et+1-Et=[(1-δE)-1]Et,即Et+1=(1-δE)Et

当t为工作日时ut=0,有:

Vt+1-Vt=[(1-δv)-1]Vt,即Vt+1=(1-δv)Vt

Et+1-Et=εEEt,即Et+1=(1+εE)Et

设工作x1天后休息x2天,再工作x3天,休息x4天……工作xn-1天,休息xn天,即:

s.t.x1+x2+...+xn=T

x1+x3+...+xn-1=(1-m)T

当t=x1(工作x1天)时,有:

Vt={V0,(1-δv)V0,(1-δv)2V0,...,(1-δv)x1-1V0}

Et={E0,(1+εE)E0,(1+εE)2E0,...,(1+εE)x1-1E0}

当t=x1+x2(工作x1天,再休息x2天)时,有:

Vt={εv,εv,εv,...,εv}

Et={(1+εE)x1-1(1-δE)E0,(1+εE)x1-1(1-δE)2E0,...,(1+εE)x1-1(1-δE)x2-1E0}

当t=x1+x2+x3(工作x1天,休息x2天,再工作x3天)时,有:

Vt={(1-δv)εv,(1-δv)2εv,...,(1-δv)x3εv}

Et={(1+εE)x1(1-δE)x2-1E0,(1+εE)x1+1(1-δE)x2-1E0,...,(1+εE)x1+x3(1-δE)x2-1E0}

当t=x1+x2+x3+x4(工作x1天,休息x2天,工作x3天,再休息x4天)时,有:

Vt={εv,εv,εv,...,εv}

Et={(1+εE)x1+x3(1-δE)x2E0,(1+εE)x1+x3(1-δE)x2+1E0,...,(1+εE)x1+x3(1-δE)x2+x4-1E0}

……

依次递推,直至t=T。将该过程代入式(1),可得到最优劳动生产率的离散动态决定式:

Lt*=V0E0+(1-δv)(1+εE)V0E0+...+(1-δv)x1-1(1+εE)x1-1V0E0+(1-δv)(1+εE)x1(1-δE)x2-1

εvE0+ ...+(1-δv)x3(1+εE)x1+x3-1(1-δE)x2-1εvE0+...+(1-δv)xn-1(1+εE)x1+x3+xn-1-1

(1-δE)x2+x4+xn-2-1εvE0

={1+(1-δv)(1+εE)+...+[(1-δv)(1+εE)]x1-1}V0E0+{(1-δv)(1+εE)+

[(1-δv)(1+εE)]2+...+[(1-δv)(1+εE)]x3}(1+εE)x1-1(1-δE)x2-1εvE0+ ...+

{(1-δv)(1+εE)+[(1-δv)(1+εE)]2+...+[(1-δv)(1+εE)]xn-1}(1+εE)x1+x3+...+xn-3-1

(1-δE)x2+x4+...+xn-2-1εvE0

(7)

由式(7)可知,基于劳动生产率最大化的公共假日最优配置结构由如下参数系统决定:休假率m、个体的精力恢复度εv、工作经验积累率εE、个人精力Vt对劳动生产率贡献率αv、工作经验Et对劳动生产率贡献率αe和工作经验损耗率δE。为了识别具体的最优假日配置模式,本文将利用离散动态算法器对系统进行高强度仿真测算。

三、仿真模拟:哪种休假模式更好?

(一)参数环境的设定

仿真测算的目的是在给定参数环境下寻求式(7)的最优化结果。为此,根据现实经验对参数系统进行如下设置,以得到假日治理的最优模式ut*。

为了测试各种情况下最优的休假模式是否稳定,不失一般性,分两种情境进行数值模拟。

情境1(现实情境):固定周休情境。此时每周7天,周末固定休息两天。

情境2(理想情境):灵活周休情境。每周依然是7天,但是周休日的位置可以在本周内灵活安排。

根据中国的实际情况,在所考察的两周内,公共假日的配置形式有三种:两周内出现一个短节日、出现一个长节日,以及短节日和长节日同时出现。

(二)非线性动态的迭代仿真

针对式(4)进行的系统混合整数非线性规划(NMIP)动态最优解,由于其求解复杂性,传统算法难以应用,本文使用多机并行的试错-修正-迭代方法确定离散动态经济解决方法。

第一步,利用软件Matlab的专用程序包(MINLP)对每日变量参数环境下进行迭代运算,以求得最优节假日安排ut*。由于变量众多,尝试将连续工作日或连续休息日作为一个变量,从而简化性能指标函数,但MINLP对解析式的计算反应迟钝。

第二步,使用软件Matlab最优求解工具箱(OPTI toolbox)处理NMIP中的解析式计算。在仅有的两种算法器中,基本开源非线性混合整数编程(BONMIN)虽然能短时间内计算出结果,但是无法保证全局最优,尝试使用不同初值进行遍历也受到电脑内存限制;而当考察期超过30天时,SCIP会因计算时间过长而导致计算终止。于是,本文使用SCIP求解情境1和情境2考察期为14天时的最优解(见表1和表2)。

第三步,考虑0-1变量特性,采用枚举的方法列出所有组合,对性能指标进行计算并记录最大值。经过多台电脑约一周的计算,得到考察期30天及以上时间的最优解(见表3)。

表1 情境1(固定周休)下的最优节假日安排

表1(续)

表1结果显示,在各种参数情况下,公共假日均匀分布在工作周内的分散休假模式都是最优的休假模式。表2结果显示,如果可以突破现有的周休制度,那么分散休假依然是最优的休假模式,能带来最高的劳动生产率。

表2 情境2(灵活周休)下的最优假日安排

表2(续)

表3 月度观测期内的最优节假日安排

表3(续)

表4 年度观测期内的最优节假日安排

表3和表4的结果与表1保持一致,增强了各观测期内迭代测算的稳健性。因此,为实现劳动生产率最大化,最优的假日配置模式都是分散休假模式,从而验证了本文理论模型的预测。

衡量高质量发展既要衡量过程也要衡量结果。上述仿真测算证实,相较于行政性集中休假,制度性分散休假有助于优化劳动生产率。至于该过程能否产生高质量发展的结果,则需要进一步评估两种休息模式对长期经济增长的影响。大量文献显示,劳动生产率会对经济增长产生积极作用[38-40]。为此,本文接下来通过检验休假集中度对各经济体经济增长的影响来验证假日配置对高质量发展的作用(4)在实证部分中并未对假日分布与劳动生产率进行直接回归,原因在于:一是劳动生产率的评估涉及工作时间,但有关各经济体工作时间的统计数据较为缺乏,难以成体系使用;二是由于统计口径不一致,各经济体对工作时间的统计结果较为驳杂,且部分发展中国家存在数据缺失或统计质量等问题。。

四、实证检验:分散式休假是否有利于高质量增长?

(一)研究设计

本部分研究假日配置模式对经济增长的影响。其验证逻辑是,如果分散休假能带来更高的劳动生产率,则有利于经济的高质量增长。此处,用假日分散度来度量分散休假模式的实现程度。

1．样本来源

本部分选取世界银行发布的《世界发展报告》所涵盖的132个成员方作为计量样本,并增加6个经济合作与发展组织(OECD)成员方为补充样本,最终根据数据可得性确定了126个经济体,形成2015—2018年动态面板数据。为了保证数据统计口径的一致性和有效性,主要数据来自世界银行数据库,唯有公共假日数据根据各经济体的节假日政策公报手工统计得来。

2．变量选取

被解释变量的选择遵循经济增长的决定框架[41],即:

gy=f(y,y*)

(8)

基于本文的理论模型,本部分的核心解释变量为该经济体当年的休假模式变量,构建假日分散度Xit来反映i经济体在第t年分散/集中休假的频繁程度和分布程度,即:

(9)

其中,Nit为i经济体第t年的假日总量(含周休日)。Mitn表示在i经济体第t年中每天的假日分布得分:如果第n个节假日的前一天或后一天是节假日,则Mitn=1;如果第n个节假日的前一天与后一天都是节假日,则Mitn=2;否则,Mitn=0。当保持节假日天数不变时,Xit越大,意味着本年度中分散休假的程度越高;Xit越小,意味着该经济体集中休假的程度越高。假日分散度可以很好地反映劳动生产率的作用,即本文理论命题的内涵。伊登(Eden,2016)发现,太长的工作日或休息日都不利于个体绩效的提高,而每周工作2～3天休息一天比连续工作5天再休息2天更为有效[25]。这意味着假日均匀地穿插在工作日中比集中休假的制度安排更能提高个体的劳动生产率,即分散休假更能发挥“玩中学”效应。

在控制变量中,首先,控制假日总量的影响。其次,人力资本(HCit)用受教育程度来体现,它与经济增长的密切关系得到国内外学者的普遍认同,测算方法主要有成本法、收入法和教育指标法[42-44]。但是,单纯用教育指标法来测度人力资本缺乏一定的准确性,受到了诸多质疑[43-44]。参考巴罗(Barro,1997)[41]的做法,引入经济发展水平作为交叉项(logGDP×男性受教育年限)表征人力资本水平,并控制预期寿命以体现人力资本中的健康资本要素。尽管有些研究认为女性的人力资本水平可以反映总体的人力资本水平,但是可能采用男性的人力资本水平来表征人力资本存量更为合理。例如,姚洋和崔静远(2015)发现中国男性的人力资本利用率要远高于女性[44]。还有学者发现25岁以上人口受教育程度比15岁以上人口受教育程度对经济增长更具解释力[41]。综上,本文选取25岁以上男性受中等和高等教育程度年限来表征人力资本[41]。此外,借鉴索基亚齐斯和安图尼斯(Soukiazis &Antunes, 2012)[46]的指标设置,采用每百万25岁以上人口拥有的专利总数来反映人力资本水平中的创新程度或质量异质性。最后,其他的控制变量还包括物质资源禀赋、出生率、通货膨胀率、贸易总额、地区哑变量等[41]。其中,物质资源禀赋用固定资本形成来衡量[41];出生率衡量一个经济体潜在新生劳动力的供给水平,经济增长水平与出生率密切相关[47];一般认为,通货膨胀不利于长期经济增长,而实现稳定的低通货膨胀是央行货币政策的重要目标,本部分采用世界银行公布的消费者价格指数(CPI)来控制通货膨胀率的影响[48];贸易总额(即进出口贸易总额)衡量了一个经济体经济的开放程度,进出口贸易可促进技术进步、人力资本积累和生产率提升,进而促进经济增长[49-50],本部分采用世界银行统计数据库中当期商品进口和出口贸易总额(现价美元)的简单加成来表示贸易总额。

由于被解释变量为人均GDP增长率,logGDP、固定资本形成、进出口贸易总额三个总量值的控制变量相应变为均值,即人均GDP、固定资本形成/GDP、进出口贸易总额/GDP。

被解释变量、核心解释变量和其他变量的描述性统计见表5。

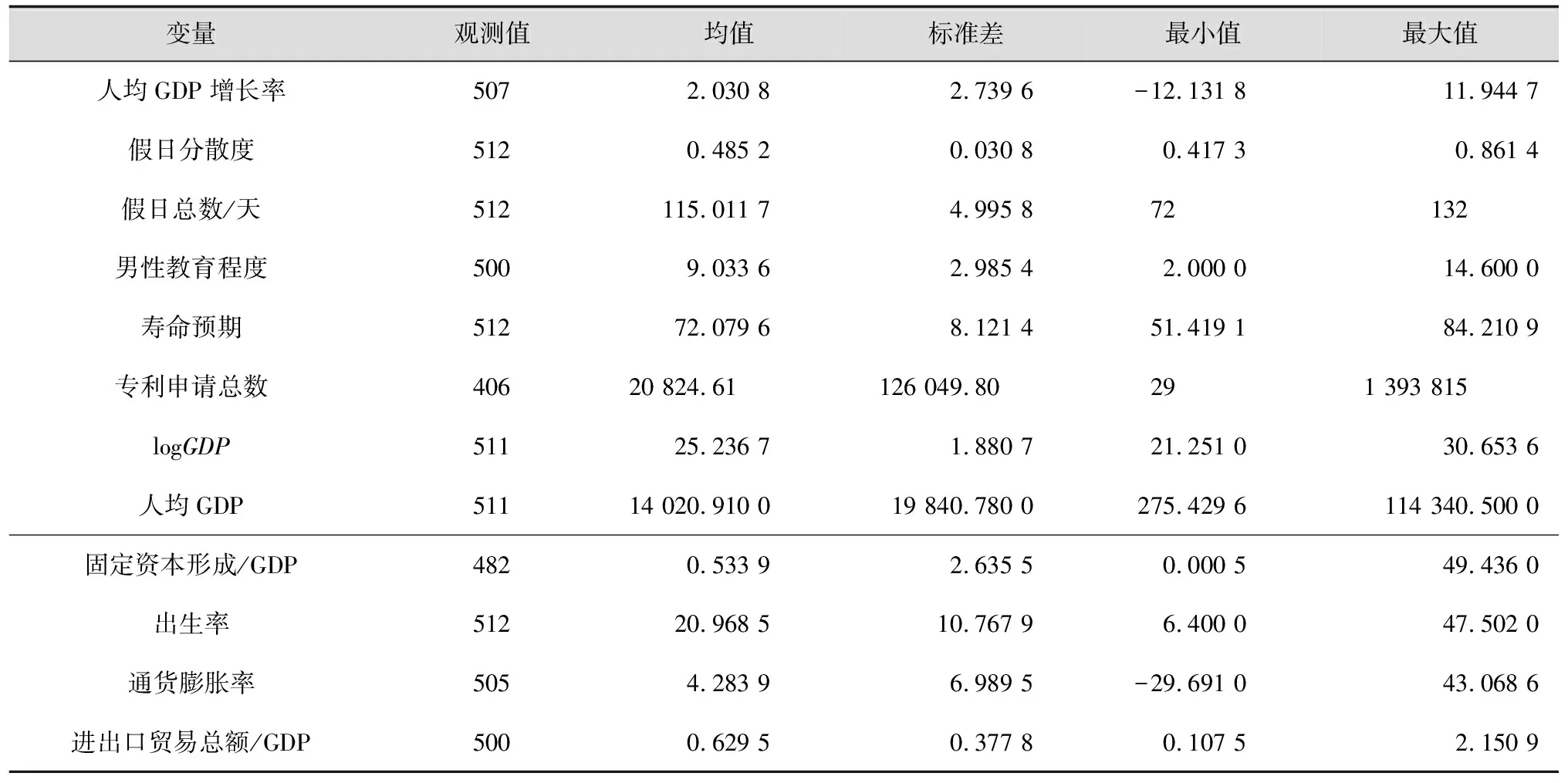
表5 变量的描述性统计

3．估计策略

由于假日总量和假日分散度可能具有一定的相关性,在基本回归中只引入假日分散度,然后再加入二者的交叉项以体现假日质量和数量的综合作用。基本评估方程为:

gyit=α+βXit+γHCit+δControlit+εit

(10)

其中,gyit为i经济体当年的人均GDP增长率;Xit为假日分散度;HCit为人力资本,包括25岁以上男性受中等和高等教育年限、预期寿命和logGDP×男性受教育程度三个变量;Controlit为一系列影响跨国(地区)经济增长的控制变量,包括人均GDP、固定资本形成/GDP、进出口贸易总额/GDP、通货膨胀率和出生率。

(二)基准回归分析

表6报告了所有样本经济体2015—2018年的基准回归结果。 结果显示,核心解释变量(假日分散度)对经济增长具有显著的正向作用。这呼应了理论模型和仿真测算的结果,说明分散休假对劳动生产率的促进最终会传导到经济增长上,进而促进高质量发展。

表6 基准回归结果

在控制变量方面,logGDP和男性受教育程度交叉项的系数显著为负,这表明更长的教育年限提高了增长对GDP的敏感度[51]。通货膨胀率、出生率、人均GDP均负向作用于经济增长的结果和巴罗(1997)[41]的分析结果一致。专利申请总数正向作用于经济增长且影响显著,而贸易进口总额和固定资本形成的效应与部分文献不符,说明有可能存在内生性问题。为此,本文将进一步检验并优化回归结果。

(三)内生性与稳健性分析

1．内生性检验

尽管表5的动态面板数据能在一定程度上缓解遗漏变量所导致的内生性问题,但依然有必要使用工具变量法和普通最小二乘(OLS)法予以解决。为此,对模型进行豪斯曼检验。表7的检验结果在1%的显著性水平上拒绝“所有解释变量为外生”的假定。

表7 内生性检验

怀特检验说明存在异方差(P=0.000 0),需要进行杜宾-吴-豪斯曼(DWH)检验。结果显示,F统计量和X2统计量的P值都小于0.05,表明模型存在内生解释变量(5)限于篇幅,省略具体回归结果,备索。。

2．工具变量法

考虑到可能存在不随时间而变的遗漏变量,通过豪斯曼方法甄别固定效应和随机效应(Prob>chi2=0.000 1),最终选择面板数据固定效应模型:

gyit=α+βXit+γHCit+δControlit+μit+εit

(11)

其中,μit用来控制经济体固定效应,消除不随经济体因素变化所造成的遗漏变量问题。

工具变量(IV)选择滞后项作为内生解释变量。第一阶段回归的F统计值为353.382,远大于10,通过了弱识别检验。然而,在使用工具变量法重新回归后,假日分散度对经济增长的影响达327.57%,而且在10%的水平上显著,说明可能遗漏了重要的解释变量。因此,本文引入年度假日数量和假日分散度的交叉项(IV1)弥补单独使用假日分散度带来的遗漏变量问题或系数高估问题,回归结果如表8所示。其中,核心解释变量(假日分散度×假日总量)对人均GDP增长率的回归系数显著为正。这表明分散的休假模式对于高假日水平经济体而言更利于经济增长,与仿真结果一致。

本文还选取当期储蓄率作为工具变量(IV2)进行回归。储蓄率与居民收入之间并不一定正相关,收入水平和居民储蓄率并不一定同步提高[52]。还有研究表明,储蓄率与经济存在非线性的峰形关系[53]或非线性影响关系[54],甚至呈现负相关的情况,尤其是对于一些成熟经济体制下的国家[55]。由表8可知,假日分散度对人均GDP增长率的回归系数仍显著为正,进一步证实了前文的分析结果。

表8 固定效应模型的工具变量回归分析

此外,经过内生性处理后,在以储蓄率为工具变量分析中,固定资本形成和人力资本对经济增长的回归系数均显著为正,与已有文献结论[56]一致。同时,出生率和通货膨胀率对经济增长的负向作用亦符合相关实证研究的结果[57]。上述情况说明内生性处理有效改善了回归质量,增强了估计结果的可靠性。

3．稳健性分析

本部分选用广义矩估计(GMM)工具变量进一步检验估计结果的稳健性。表9的IV1结果显示,核心解释变量(假日分散度×假日总量)依然正向作用于经济增长,进一步增强了前述回归的稳健性。

表9 GMM工具变量回归分析

五、结论、启示与建议

(一)研究结论

本文对工作-闲暇选择的内部机制进行理论解构,进而基于抗疲劳效应和经验效应建立离散动态的公共假日治理模型,并设置符合中国国情的参数环境,对模型进行仿真测算。仿真结果显示,制度性分散休假模式比行政性集中休假模式更能优化劳动生产率。实证研究结果显示,越是分散的休假模式越有利于提高经济增长率。本文通过理论建构与实证分析证实,分散休假的假日治理模式更有利于促进经济的高质量发展。

(二)政策启示

从假日总量来看,中国的公共假日总数已居于较高水平(全年已达115天),与美国、日本、印度等国的公共假日水平接近,如图3所示。根据工作-闲暇选择的劳动供给理论,在闲暇水平较高时,进一步增加闲暇水平(公共假日)的边际效应递减并会挤出工作时间和经济产出。与此同时,中国的劳动生产率与美国、日本、韩国等发达国家还存在较大差距。由此,不增加假日总量、通过假日分布的结构优化来提高劳动生产率更具经济价值和现实必要性。为此,在保持假日总水平不变的情况下,需更加关注假日制度的稳定性和制度化,按照节假日的自然节律尽量使公共节假日在全年均匀分布,使人们在每个季节、每个工作周期内都能得到有规律的休假、休养,形成稳定的预期,降低由于挪假带来的拥堵、协调、错配等菜单成本。同时,需要企业假期和个人假期制度配合公共假日制度的改革,尽快落实带薪休假制度,使分散的公共假日和灵活的带薪休假相结合,满足人们探亲、旅游的长假需求。

图3 1995—2018年部分国家的公共假日

(三)政策建议

根据本文的理论论证及其仿真推演,结合国际假日制定的经验,对中国的假日改革和假日调整政策提供以下建议:

第一,启动新一轮假日改革论证工作,将假日调整的思路从增减总量转向优化结构。建议进一步弱化以黄金周为代表的集中休假制度,可继续取消“十一”黄金周(只保留春节黄金周)代之以增加1～2天传统节日(如重阳节)。应使全年的节日尽量均匀分布在各个月内并固定日期,遇上周休日时相应前移或后移。

第二,创新落实带薪休假制度,鼓励个人的带薪休假和国家的公共假日灵活结合以满足国民的长假需求。落实带薪休假是经济高质量发展的必然要求,也是社会发展演进的国际惯例。职工可结合带薪假期和法定公共假日,形成个性化、分散配置、灵活机动的长假,以满足休闲度假质量的需求和传承弘扬传统文化。实际上,中国职工根据工龄已被分别赋予5～15天的法定带薪休假,但在落实中还存在诸多难点。下一步,应强化和创新对带薪休假的落实措施。为此,需要探讨分阶段、分行业、分地区的示范、试点,可考虑先在政府机构、事业单位、国有大中型企业逐步落实,随后在全国范围内全面落实。此外,可借鉴其他国家的经验,如德国通过工会系统和法律机构促进带薪休假权利的落实[58],还可根据企业落实带薪休假的天数,对企业的所得税按比例实施减免奖励。

第三,尝试试点每周2.5天休假制度,探索分散休假的新手段、新模式。2015年,《国务院办公厅关于进一步促进旅游投资和消费的若干意见》(国办发〔2015〕62号)鼓励有条件的地方和单位根据实际情况,依法优化调整作息安排。此后,包括江苏、河北、江西等省份陆续出台了鼓励2.5天休假的意见。值得注意的是,新冠疫情期间,多地(如江西、浙江和甘肃陇南)陆续出台政策鼓励推行每周2.5天休假,即如果职工在每周的前四天半能干完一周的既定工作,则可在周五下午提前开始双休日假期。2.5天弹性休假是推进分散休假、激发劳动生产率的有益探索,也是向更为灵活、高效的假日治理制度的过渡性尝试,可以在不断总结各地经验的基础上鼓励有条件的企业积极试点2.5天休假制度,探索更多具有中国特色的分散休假模式。