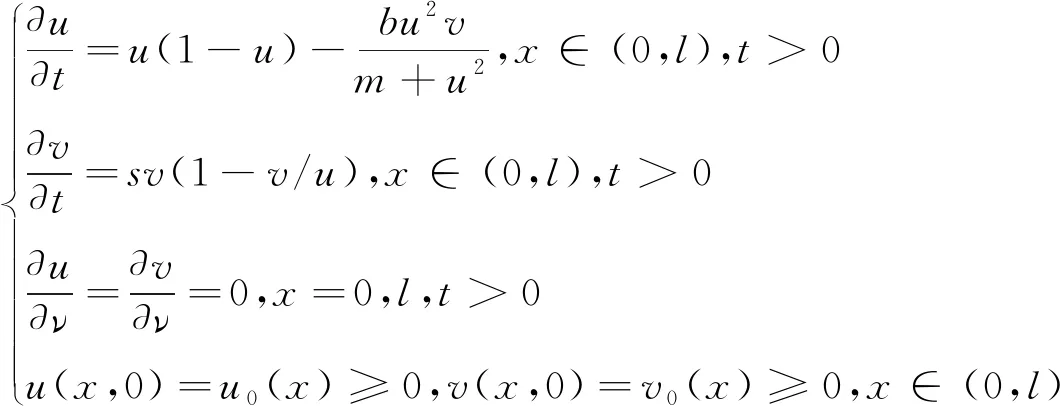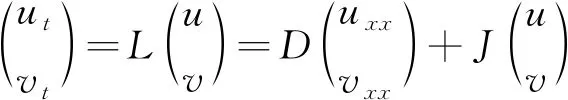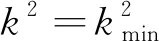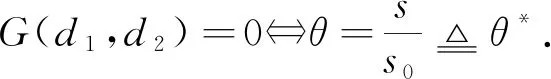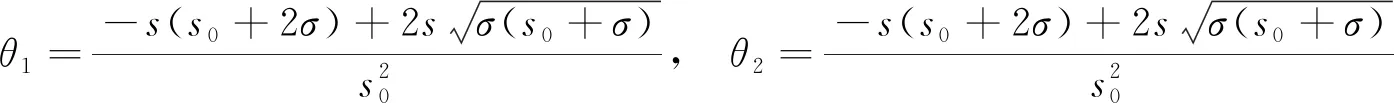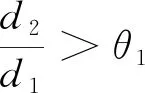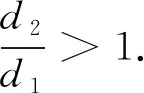一类扩散Leslie型捕食-食饵模型的动力学性质
2023-12-04李彦,陈博
李 彦, 陈 博
(淮阴师范学院 数学与统计学院, 江苏 淮安 223300)
0 引言
众所周知,数学生态模型在理解种群相互作用及演化中发挥重要作用.特别地,捕食-食饵模型作为一种重要的两种群关系,近年来得到了广泛研究.一类经典的Gause型捕食-食饵模型呈如下形式[1]

(1)
其中u和v分别表示食饵和捕食者的种群密度.g(u)表示在没有捕食者的情况下食饵种群生长函数.功能反应函数p(u)描述了捕食者对食饵的猎食关系进而产生对食饵种群密度的影响.常见的功能反应函数有Holling型、Beddington-DeAngelis型等.函数q(u)描述了捕食者如何将被捕食的猎物转化为捕食者的生长,一般取q(u)=p(u).参数c表示捕食者将被捕食的猎物转化为其生长的效率,而d表示捕食者的死亡率.
若取g(u)=r(1-u/K),q(v/u)=s(1-v/hu),d=0时,模型(1)变化为

(2)

系统(2)中若取p(u)为Holling II型,则称之为 Holling-Tanner型[3].文[4]中认为,系统(2)中Holling II型功能反应可以被其他类型所替换,如Holling III型或HollingIV型.关于带有不同型功能反应的捕食-食饵模型的研究也有很多研究成果[5-12].
在物种演化过程中,由于多种原因(环境因素、食物供应等)的影响,个体在空间中不固定,其空间分布不断变化.因此,在种群模型中引入了空间影响如种群扩散是合理的.Turing[13]的经典工作表明,化学反应和扩散的相互作用会导致平衡点从局部系统的稳定到扩散系统的不稳定,从而导致空间模式生成.关于生态学、流行病学化学等领域中对反应扩散系统Turing不稳定性和模式生成的研究还有很多研究[13-19].
受上述文献启发,并对系统(2)作适当的变换后,本文考虑如下带有齐次Neumann边界条件以及Holling III 型功能反应扩散捕食模型
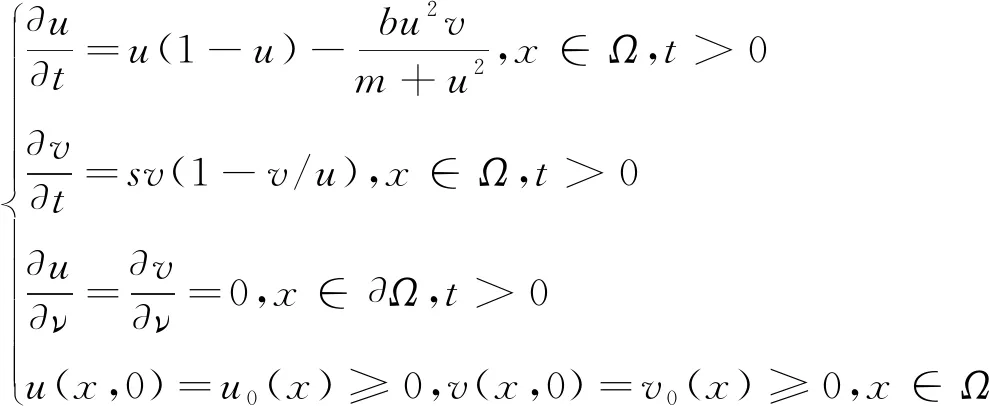
(3)
其中u(x,t)和v(x,t)分别表示食饵和捕食者的种群密度,Ω⊂RN(N≤3)是具有光滑边界∂Ω的有界域,v是边界∂Ω的外单位法向量.齐次Neumann边界条件表明捕食系统是自封的,即边界上种群流量为零.常数b>0,m>0,正常数d1和d2表示扩散系数,u0(x)和v0(x)为非负连续函数.
第1节,讨论系统(3)对应常微分系统正平衡点的稳定性和Hopf分支周期解.第2节,考虑系统(3)正平衡点的Turing 不稳定性及Hopf分支周期解.
1 常微分系统的稳定性和Hopf分支
本节讨论常微分系统

(4)
正平衡点的稳定性及Hopf分支周期解.求解代数方程组
(5)
当γ=2(b-1)3-9m(b-1)-27m<0时,系统(4)存在唯一正平衡点u*=(u*,v*),其中
其中μ=3m-(b-1)2.记u=(u,v)和
那么,G(u)在u*处的线性化形式为

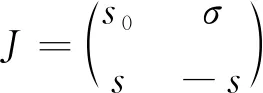
(6)
记矩阵(6)的特征多项式为
P(λ)=λ2-TrJ·λ+DetJ,
其中TrJ=s0-s,DetJ=-s(s0+σ).
易见DetJ>0.为保证s0的正性,假设
(H)bu*((u*)2-m)>(m+(u*)2)2.
于是,通过判别TrJ的符号便容易得到u*稳定性.因此,有以下结论.
定理1 假设条件(H)成立.若s>s0,则系统(4)的正平衡点u*是局部渐近稳定的;若s 令λ(s)=α(s)±iβ(s)为P(λ)=0在当s在s0附近时的一对复根.于是 因此,α(s0)=0,α'(s0)=-1/2<0.这意味着横截条件满足,因而系统(4)在s通过s0时从u*处产生Hopf分支. 因此,系统(4)转化为 (7) 系统(7)可表示为 (8) 其中 f(u,v,s)=A20u2+A11uv+A02v2+A30u3+A21u2v+…, g(u,v,s)=B20u2+B11uv+B02v2+B30u3+B21u2v+B12uv2+…, 按照文献[20]中的计算过程,有 (9) 利用Poincar’e-Andronov-Hopf分支定理,可以得到如下结果. 定理2 假设条件(H)成立.当s=s0时,系统(4)在u*处产生Hopf分支. 1)a(s0)决定分支周期解的稳定性:若a(s0)<0(>0),则分支周期解是稳定的(不稳定的); 2)μ2决定Hopf分支的方向:若μ2>0(<0),则Hopf分支是超临界的(次临界的). 在齐次Neumann边界条件下,u*也是扩散系统(3)的正平衡点.本节分析系统(3)的u*的Turing不稳定性的条件.在这里,考虑一维区间Ω=(0,l)中零流边界条件的情形 (10) 其中l>0是区间长度.令 其中λ是关于时间t的扰动增长率,ρ1和ρ2是振幅,k是解的波数.系统(10)在u*处可线性化为 (11) 其中D=diag(d1,d2),J是由式(6)所定义的Jacobian矩阵.L是线性算子,其定义域为DL=XC=X⨁iX={x1+ix2:x1,x2∈X},其中 H2[(0,l)]表示标准的Sobolev空间.记 明显地,算子L的特征值由矩阵Jk的特征值给出.Jk的特征方程为 Pk(λ)=λ2-TrJ(k)·λ+DetJ(k)=0 (12) 其中 TrJ(k)=s0-s-k2(d1+d2), DetJ(k)=d1d2k4+(sd1-s0d2)k2-s(s0+σ). 特征方程(12)的根,得出扩散关系 如果bu*((u*)2-m)<(m+(u*)2)2,那么s0<0.易见TrJ(k)<0和DetJ(k)>0.从而,Pk(λ)=0的两个根都有负实部.因此,有以下结论. 定理3 假设bu*((u*)2-m)<(m+(u*)2)2.则系统(10)的正平衡点u*局部渐近稳定. 由定理1知,假设条件(H)成立,当s>s0时,常微分系统(4)的正平衡点u*渐近稳定.现在,研究系统(10)的正平衡点u*的稳定性.当条件(H)成立,s0>0,DetJ(k)>0.当特征方程(12)至少有一个根有正实部时,系统(10)的正平衡点u*不稳定.因此,特征方程(12)无带正实部的虚根.注意到当s>s0时,TrJ(k)<0.因此,特征方程(12)无正实部的虚根. 定义关于k2是二次多项式 φ(k2)=DetJ(k)=d1d2k4+(sd1-s0d2)k2-s(s0+σ). 令 于是 注意到DetJ=-s(s0+σ)>0和σ<0,从而 因此,Λ(d1,d2)=0有两个正实根 (13) 基于上述分析,得到以下的Turing不稳定性的结果. 定理4 假设条件(H)成立和s>s0(因此局部系统(4)的正平衡点u*稳定).对于θ1>0,存在无界域U={(d1,d2):d1>0,d2>0,d2>θ1d1},对任意(d1,d2)∈U,u*对于反应扩散系统(10)是不稳定的,即表明Turing不稳定性发生. 类似于定理2,对扩散系统(10)在与常微分系统模型(4)相同的分支点上进行Hopf分支分析,而且在s=s0附近存在空间齐次分支周期解.由于扩散的影响,系统(10)周期解的稳定性可能与局部系统(4)不同.应用Hassard[21]中的规范型理论和中心流形定理,研究系统(10)Hopf分支的方向以及分支周期解的稳定性. 由文[20]的计算过程,可得 于是,可得如下结果 定理5 假设条件(H)成立,那么系统(10)在s=s0产生Hopf分支. 1) 若Re(c1(s0))<0,则Hopf分支的方向是次临界的且分支周期解轨道渐近稳定; 2) 若Re(c1(s0))>0,则Hopf分支的方向是超临界的且分支周期解轨道不稳定.
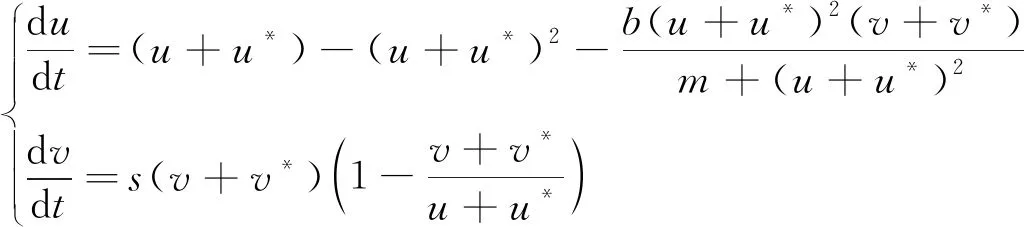
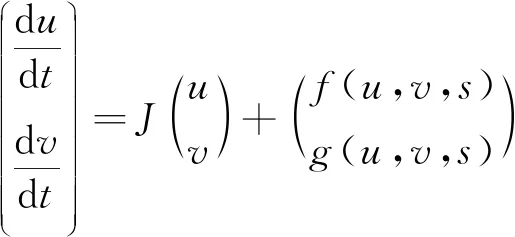
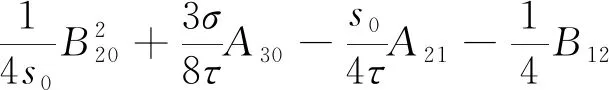
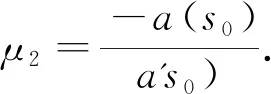
2 扩散系统的时空动力学