二维半线性椭圆方程边值问题的牛顿迭代法

牟行洋

(江汉艺术职业学院 管理学院, 湖北 潜江 433100)

0 引言

长期以来,半线性椭圆型方程一直受到人们的广泛关注.其原因是因为许多数学物理问题,如源于非线性源的非线性扩散理论[1],热力学中的气体燃烧理论[2-3],量子场论和统计力学[4-6]以及星球系的重力平衡理论[2,7]都与它有着极大的渊源.而且,数学内部的许多分支,如几何中的Yamabe问题[8]和等周不等式[9],调和分析中的Hardy-Littlewood-Sobolev不等式[10],Yang-Mills泛函的非极小解存在性[11]以及人口动力系统[12]等问题都与之有着深刻的联系.

许多学者研究了二维半线性椭圆方程正解的存在性[13-18],其中刘伟和芮洪兴利用二重网格混合元算法求解了二维半线性椭圆问题的混合元解[19],大大降低计算量,提高计算效率.麦雄发,胡淑娟和丁方允针对一类半线性椭圆边值问题,利用有限元给出了一种一般迭代数值的方法,收敛定理,误差估计[20].因此,对于这一类方程的研究无论是在理论上,还是在实际应用上都有着非常重要的意义.本文利用有限元方法结合牛顿法研究了二维半线性椭圆方程的边值问题,推导出了它的牛顿迭代式,该算法采用Matlab编制程序,具有易编程实现,求解速度快,计算精度高等优点,证明该方法的可行性和有效性.

1 数学模型

考虑如下的二维半线性椭圆方程数学问题:

(1)

其中Ω是R2上的有界闭区域,边界∂Ω=Ω1∪Ω2分片光滑且Ω1与Ω2互不相交,a(x,y)≥a0>0,f(x,y),φ(x,y),β(x,y)都是关于(x,y)的二维光滑函数,σ为大于等于零的常数,n是边界上的外法线方向,g(u)是关于u的非线性函数.当这些函数都是已知条件求解u时,是二维半线性椭圆方程的数学模型.对于问题(1),在Ω1上给出Dirichlet边界条件,在Ω2上给出Robin边界条件,特别地,当σ=0时是Neumann边界条件.

2 牛顿迭代法

引入Sobolev空间H1(Ω)的子空间V={v∈H1(Ω):v|Ω1=0},在式(1)中第一个式子的两端用v(x,y)作内积,有

(2)

由泰勒公式有

g(uk)=g(uk-1)+g′(uk-1)(uk-uk-1)+o(uk-uk-1),k=1,2,3,…

(3)

由式(2)和式(3)得迭代形式如下

(g(uk-1)+g′(uk-1)(uk-uk-1),v)=(f(x,y),v),k=1,2,3,…

(4)

对上式应用格林公式,得

(5)

将式(1)中第三个式子变形为

(6)

将式(6)代入式(5),得

(7)

式(7)称为式(1)的牛顿迭代格式.

3 数值算例

在单位矩形Ω={(x,y)|0≤x≤1m,0≤y≤1m}上求解问题

其中

a(x,y)=2x+3y,

真解

u(x,y)=x2y2(1-x)(1-y),

将有界区域Ω沿x,y方向作均匀三角剖分,剖分的步长h=0.05,采用Lagrange插值基函数分4种类型讨论,分别是一次、二次和三次,此时它们的自由度分别为441个、1681个、3721个.

情形1 四次偶非线性g(u)=u4.

f(x,y)=-4xy2(1-x)(1-y)+2x2y2(1-y)-2y2(2x+3y)(1-x)(1-y)-4xy2(2x+3y)(1-y)-

6yx2(1-x)(1-y)+3x2y2(1-x)-2x2(2x+3y)(1-x)(1-y)-4yx2(2x+3y)(1-x)+u4.

将g(u)代入式(7),得牛顿迭代式(8).取初值U0=0,根据已知的边界条件进行迭代计算,此处仅讨论Dirichlet边界条件,Neumann和 Robin边界条件讨论方法类似进行.在不同的基函数下,数值解剖分图见图1,真解与数值解的误差剖分图见图2-4,对应的迭代次数、L2误差、最大误差和CPU运行时间计算结果见表1.

表1 在不同基函数下对应的迭代次数、L2误差、最大误差和CPU运行时间的计算结果

(8)

情形2 五次奇非线性g(u)=u5.

f(x,y)=-4xy2(1-x)(1-y)+2x2y2(1-y)-2y2(2x+3y)(1-x)(1-y)-4xy2(2x+3y)(1-y)-

6yx2(1-x)(1-y)+3x2y2(1-x)-2x2(2x+3y)(1-x)(1-y)-4yx2(2x+3y)(1-x)+u5.

将g(u)代入式(7),得牛顿迭代式(9).取初值U0=0,根据已知的边界条件进行迭代计算,在不同的基函数下, 数值解剖分图见图5,真解与数值解的误差剖分图见图6-8,对应的迭代次数、L2误差、最大误差和CPU运行时间计算结果见表2.

表2 在不同基函数下对应的迭代次数、L2误差、最大误差和CPU运行时间的计算结果

(9)

情形3 奇有界g(u)=sinu.

f(x,y)=-4xy2(1-x)(1-y)+2x2y2(1-y)-2y2(2x+3y)(1-x)(1-y)-

4xy2(2x+3y)(1-y)-6yx2(1-x)(1-y)+3x2y2(1-x)-

2x2(2x+3y)(1-x)(1-y)-4yx2(2x+3y)(1-x)+sinu.

将g(u)代入式(7),得牛顿迭代式(10).取初值U0=0,根据已知的边界条件进行迭代计算,在不同的基函数下, 数值解剖分图见图9,真解与数值解的误差剖分图见图10-12,对应的迭代次数、L2误差、最大误差和CPU运行时间计算结果见表3.

(10)

表3 在不同基函数下对应的迭代次数、L2误差、最大误差和CPU运行时间的计算结果

情形4 偶有界g(u)=cosu.

f(x,y)=-4xy2(1-x)(1-y)+2x2y2(1-y)-2y2(2x+3y)(1-x)(1-y)-4xy2(2x+3y)(1-y)-

6yx2(1-x)(1-y)+3x2y2(1-x)-2x2(2x+3y)(1-x)(1-y)-4yx2(2x+3y)(1-x)+cosu.

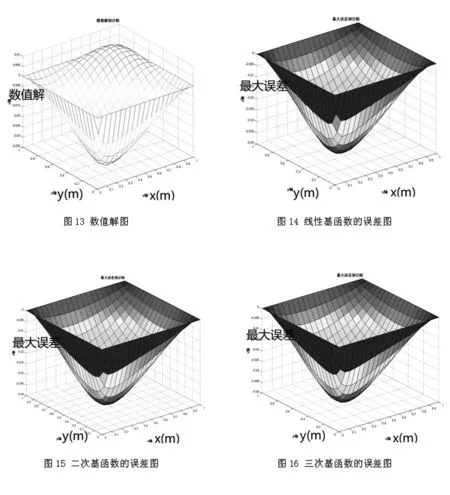
将g(u)代入式(7),得牛顿迭代式(11).取初值U0=0,根据已知的边界条件进行迭代计算,在不同的基函数下,数值解剖分图见图13,真解与数值解的误差剖分图见图14-16,对应的迭代次数、L2误差、最大误差和CPU运行时间计算结果见表4.

(11)

表4 在不同基函数下对应的迭代次数、L2误差、最大误差和CPU运行时间的计算结果

4 结论

利用有限元结合牛顿法求解了一类二维半线性椭圆方程边值问题,体现了此方法的可行性和有效性.无论是四次偶非线性情形还是五次奇非线性情形,在相同的基函数下对应误差的大小变化不大,但是,随着插值基函数次数的增加,两类误差越来越小,且代数精度较高.奇有界情形两类误差的大小变化不大,代数精度较高且相对较稳定;偶有界情形两类误差的大小虽然变化不大,但代数精度相对较低.