基于卷积神经网络的双馈风电机组独立变桨距优化控制方法
2023-12-04郑建锋
郑建锋
(华电(浙江)新能源有限公司,杭州 310009)
风电机组独立变桨距控制是风电机组实践应用过程中的重要组成部分。传统的独立变桨距控制方法多设定为单向,参考文献[1]和文献[2],设定传统Wiener 模型风电机组独立变桨距控制方法和传统FAST 风电机组独立变桨距控制方法。此类控制方法可以实现预期的控制任务,但是缺乏针对性和具体性,会使不平衡载荷更加明显,导致桨叶产生大范围的挥舞和摆振,严重影响风电机组传动机构等部件的机械应力和疲劳寿命,进而引发电力事故[3]。为此,提出基于卷积神经网络(Convolutional Neural Networks,CNN)的双馈风电机组独立变桨距优化控制方法。CNN 是一类包含卷积计算且具有深度结构的前馈神经网络,将其与风电机组独立变桨距优化控制工作相结合,可实现风电机组的优化控制,形成双向控制结构,改善实际控制效果,为相关技术及行业的发展奠定坚实基础[4]。
1 设计双馈风电机组独立变桨距卷积神经网络控制方法
1.1 明确风电机组独立变桨距控制指标
双馈风电机组独立变桨距优化是一个漫长的过程,需要明确控制范围,调整对应的控制指标[5]。机组动态载荷控制主要是指对机组发电情况的一种判定,结合贝兹极限理论,需要进行理想风轮气流情况的研究。
在质量守恒定律的限制下计算出风轮的净速度,计算公式为
式中:A为风轮的净速度;g为控制范围;d为机组压缩比;t为风速变化值;s为静压力差。设置摆振载荷比为3.2,风轮旋转角速度的最佳变化差值为1.26 ~2.04 rad·s-1。
1.2 风电机组疲劳载荷多目标计算
结合雨流计数(Rain Flow Counting,RFC)法,先明确当前疲劳的载荷范围、幅值以及均值,具体公式分别为
式(2)~(4)中:Sɑ、Sb和Sc分别为风电机组疲劳的载荷范围、幅值以及均值;Smax为疲劳载荷限制最大值;Smin为疲劳载荷限制最小值。
判定出此时双馈风电机组的运行实况后,需要控制与标定独立变桨距扰动现状,尽量减少风机的不平衡载荷状态,保持实际的控制稳定。
1.3 构建卷积神经网络机组独立变桨距优化控制模型
先在机组的控制程序中设置一定数量的控制节点。这些节点相互关联,形成一个循环性的控制结构。然后,依据卷积神经网络设计模型的执行结构,如图1所示。
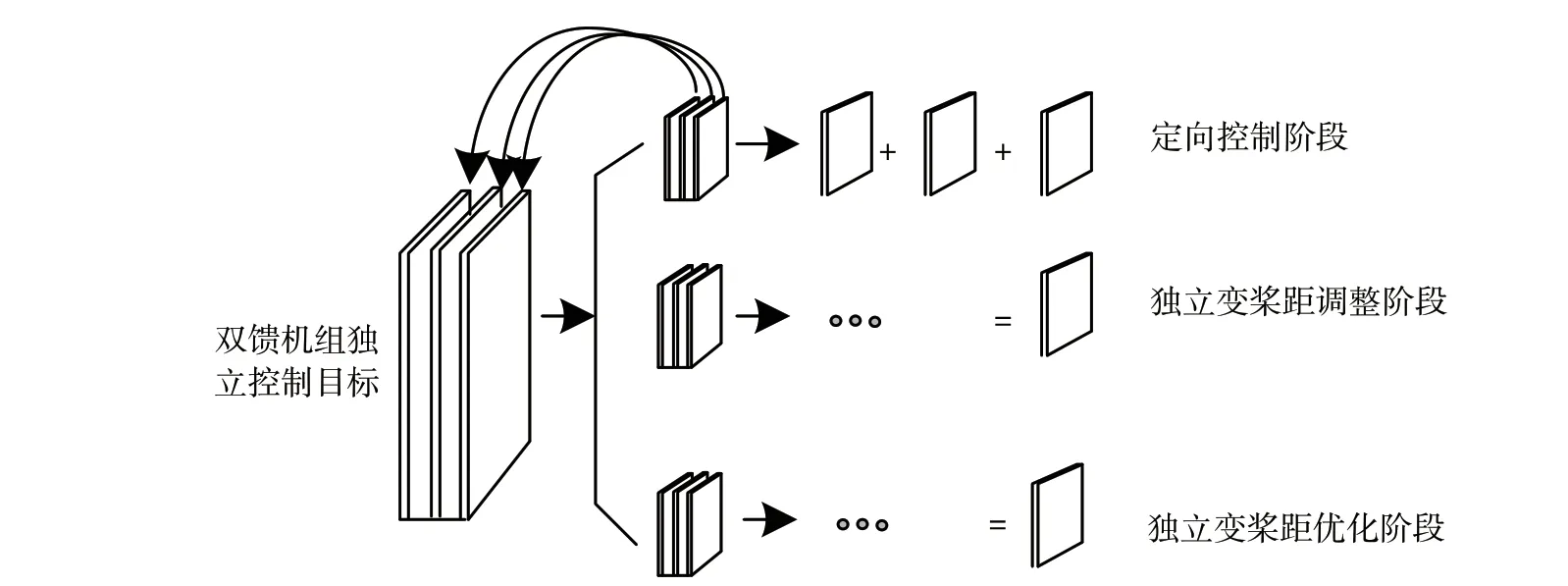
图1 卷积神经网络机组独立变桨距优化控制结构图
在模型中建立一个独立变桨距优化矩阵,并设定对应的优化目标。变桨距的调整设定距角为60°~85°。在运行过程中,确保风电的输出功率小于额定功率,形成一个闭环的控制结构,利用模型的辅助控制程序,确保双馈风电机组平稳运行,改善模型的应用效果[6-7]。
1.4 反馈校正实现优化控制
反馈校正是对模型处理过的控制结果进行校正调整。设置3 个阶段的校正标准,如表1 所示。

表1 多阶段反馈校正标准设置表
依据表1 标准,结合设计的优化模型,优化每一个阶段的风电机组独立变桨距控制,校正误差控制区域,确保最终控制效果的真实性和稳定性。
2 实验测试
在浙江华电弁山风电场“面向多机型风电机组通用性自主可控关键技术研究与应用”项目研究的过程中,发现双馈风电机组独立变桨距控制方面还存在较大提升空间。为解决项目开展过程中存在的不平衡载荷问题,验证提出的基于卷积神经网络的双馈风电机组独立变桨距优化控制方法的应用性能,设计对比实验进行测试。考虑最终测试结果的真实性与可靠性,采用对比的方式展开分析,选定H 区域的风电场作为测试的主要目标对象,参考文献设定传统Wiener 模型风电机组独立变桨距控制测试组、传统FAST 风电机组独立变桨距控制测试组以及此次所设计的卷积神经网络风电机组独立变桨距控制测试组,3 个测试组分别以A、B、C 来表示。
2.1 测试过程
设置H 区域的风电场双馈风电机组独立变桨距优化控制测试环境,布置基础的控制平台,关联主控系统、变桨距控制系统、变流控制系统以及安全链保护系统。设定风电机组的输入功率变化比为2.16,优化控制周期为5 个,促使发电机装置处于待机/顺桨状态。根据发电机输出功率的实际变化情况,调节桨距角的对应大小,进行基础测试指标及参数的设置如表2 所示。另外,结合卷积神经网络技术,调整风电机组独立变桨距的控制效果。

表2 基础测试指标及参数设置表
2.2 结果分析
测试选定的H 区域双馈风电机组独立变桨距优化控制方法,分析双馈风电机组的输出功率状况,如图2 所示。

图2 双馈风电机组的输出功率状况图
结合图2 可以看出,输出功率波动段便是机组独立变桨距需要优化控制的阶段。利用卷积神经网络技术,设定当前独立变桨距的最优角度为35°,失速调节标准差值为3.2。利用卷积神经网络对双馈风电机组进行闭环控制调节,并将设定的控制目标导入当前卷积神经控制程序,实现整体的优化控制,计算挥舞载荷标准值。挥舞载荷标准值公式为
式中:κ为载荷峰值;π为目标函数;F为堆叠控制区域;Y为偏航载荷差值。结合当前测试,对比分析测试结果数据,如表3 所示。

表3 测试结果数据比对分析表
结合表3 可知,对比测试组A、测试组B,此次设计的测试组最终得出的挥舞载荷标准值均在7 以上,说明在卷积神经网络的辅助下,当前所设计的控制方法更为高效,具有实际的应用价值。
3 结语
与初始的风电机组独立变桨距优化控制方法对比,结合卷积神经网络技术设计一个更加灵活、多变的控制结构,从多个角度扩大控制的覆盖范围,保障机组安全。此外,使用卷积神经网络可以加强对风电机组实时动态状况的把控,进一步提升控制程序的可行性和可靠性,为后续风电机组控制技术的创新与完善提供参考依据。
