面向荧光材料研究的光度学基础

翟月利，徐 坚

（河南理工大学 物理与电子信息学院，河南 焦作 454000）

1 引言

随着荧光材料制备和封装技术的不断成熟，以发光二极管（LED）和激光二极管（LD）为代表的荧光转换型（Phosphor-converted,pc）固态照明光源正在快速取代传统光源[1-4]。近年，由于固态照明技术在亮度和小型化方面的持续发展，荧光材料也正经历着不断升级迭代的过程。例如材料在形态上的逐渐多样化，从以粉体为主，逐渐发展为单晶[5-8]、陶瓷[4-6,9-12]、荧光玻璃[5-6,13-15]以及薄膜[5-6,16-18]等多种形态并存。而相关材料学的研究范围也从以结构化学、固态化学、光谱学为主开始向工程光学领域拓展。例如，近期一些利用散射调控[19-20]和光学镀膜[15]技术制备的荧光材料被应用在荧光转换白光激光二极管（pc-wLD）器件上，表现出高于传统材料的优异性能[21-23]。

光度学作为工程光学的一个分支，对于荧光材料研究者而言可谓既熟悉又陌生。熟悉的是流明效率（Luminous efficacy）、光通量（Luminous flux）等参数[24-25]在研究中被广泛地测量和讨论；陌生的是对一些光度学参数的理解存在一定的偏差，如光强（Luminous intensity）、光出射度（Luminous exitance）、光亮度（Luminance）、光照度（Illuminance）等[24]。对光度学参数理解的缺失，可能会导致相关的研究陷入误区。例如，相当数量的pc-wLD 用荧光材料的研究致力于追求峰值光通量而忽视光亮度，导致研究的方向和设计初衷产生了一定的偏差。

本文将对相关光度学参数的定义展开详细的解释，并梳理各参数之间的关系；结合实际的研究案例，探讨基于光度学参数的实验设计思路。

2 主要光度学参数及逻辑关系

2.1 光通量：流明（lm）

由图1 可知，光通量是各光度学参数的核心，是指人眼主观感知到的光源所发出的辐射功率，单位为流明（lumen,lm）。与光通量直接相关的参数是辐射功率（光功率），即光源在单位时间内辐射出的总能量[26-27]，单位为瓦特（W）。由于人眼对各波长光的敏感度不同[28]，对于同等光功率的光源，实际光通量可能有较大差异。例如，1 W、555 nm 单色光源的光通量可达683 lm，而450 nm 对应的光通量却仅有22 lm。这是因为基于光功率计算光通量时，需要乘以人眼的敏感系数。例如，人眼对555 nm 光的敏感系数为1，而 450 nm 仅为0.038。将人眼对各波段的敏感系数相连，由此得到的人眼敏感系数与波长的关系称为视见函数V(λ)。实际应用中的照明光源多为宽谱光源，利用分光光度计可获得各波段光功率分布函数S(λ)，对该函数进行积分即可获得该宽谱光源的总光功率。此时，对光功率分布函数和视见函数的乘积进行积分，再乘以单位功率是555 nm 单色光源的光通量（683 lm/W），可得该宽谱光源的总光通量[24,29]，如公式（1）所示：

其中，Φ为光通量，λ为波长。由公式（1）获得光通量之后，除以发光面积可获得光出射度，即发光表面单位面积发出的光通量为光源的光出射度[24]，单位为流明/平方米（lm/m2），如公式（2）所示：

其中，M代表光出射度，A代表发光面积。

2.2 发光强度：坎德拉（cd）

发光强度[24]（光强）可以理解为单位“发射角度”内的光通量。在二维空间上，发射角度相对比较具象。而一个光源发光实际是在三维空间发射的，因此需要在二维角度的基础上引入一个三维发射角度的概念：立体角[24]。立体角定义为所截球面面积与半径平方的比值，如图2 所示，单位是球面度（steradian,sr），对应二维的弧度。对于一些特殊情况下的立体角，如单面发射和三维空间发射的光源，对应的立体角分别为2π 和4π。综上，光源的光强[24]可以表示为公式（3），单位为坎德拉（candela,cd）：

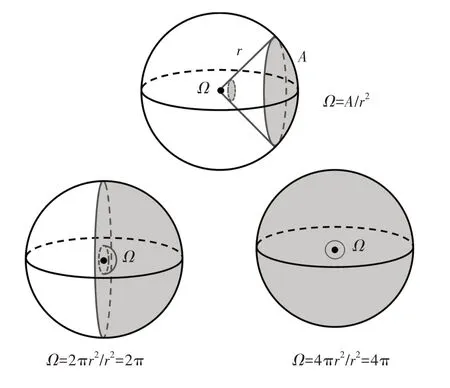
图2 典型的立体角示意图Fig.2 Typical solid angle diagram

其中，I代表发光强度，Ω代表立体角。

相较于光通量，光强是更早被定义和用来评价光源“明暗”的指标，单位为坎德拉（candela,cd），是国际单位制中7 个基本单位之一。值得注意的是，光强的单位最早是candle 而不是candela。早在19 世纪六十年代，英国学者把一只蜡烛的光强定义为1 烛光（1 candle）。20 世纪初，随着电灯的普及，光强的定义更新为“一组45 只白炽灯发光强度的1/45 定义为1 国际烛光（international candle）”。到了1948 年，光强的定义为“标准大气压下，金属铂凝固点温度下的黑体在垂直方向每1/60 cm2的光强为1 烛光”，并改candle 为蜡烛的拉丁文“candela”，即现在的国际标准单位：candela（坎德拉）。该“烛光”在数值上略小于“国际烛光”。

2.3 光亮度：坎德拉/平方米（cd/m2）

首先需要说明的是，光亮度“luminance”在一些场景中会和亮度“brightness”混用。实际上，亮度“brightness”并不是一个被定义的物理量，更多的是一种基于主观感知的一个相对标准。例如，当我们调节手机屏幕的“亮度”百分比和定性描述大功率以及高光输出的光源时，采用“brightness”；而当科研和生产中需要定量描述“亮度”时，则需要利用光度学物理量光亮度“luminance”来描述。例如，笔者随机测试某型号手机的屏幕亮度，在色温～6 700 K 时，5 个随机点在垂直方向的峰值光亮度分别为802，803，803，804，804 cd/m2。此处，笔者倡议在具有相关专业性的论文中更多地使用物理学参数光亮度“luminance”，相对减少使用主观的亮度“brightness”来描述光源。

光亮度的定义为：单位投影面积内的光强[24]，单位为坎德拉/平方米（cd/m2）。由于存在cosθ的角度分布，当描述一个光源的光亮度时，严谨的说法是要说明观测角度，由此可以表示为公式（4）：

其中，L代表光亮度，I代表发光强度，A代表投影面积，θ代表观测角度。例如，当前描述一款显示器的亮度时，往往默认的是垂直方向。有一类光源比较特殊，符合朗伯体发射[30]，如图3 所示，即各个角度的光强符合余弦分布:

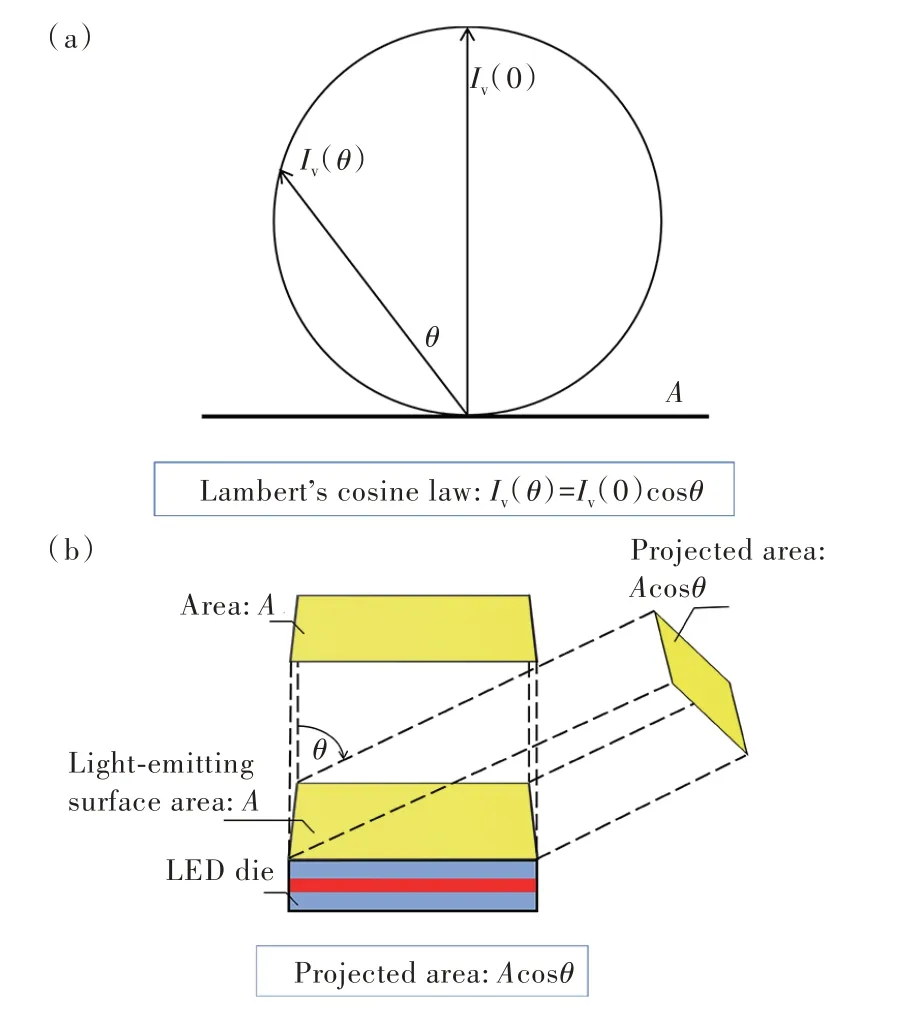
图3 朗伯体光源示意图。（a）发光强度特性；（b）发射表面特性。Fig.3 Diagram of Lambertian light source.（a）Property of the luminous intensity.（b）Property of the emitting surface.

其中，Iθ代表与垂直方向夹角为θ的发光强度，即Iv(θ)，I0代表垂直方向上的发光强度，即Iv(0)。该类光源的光亮度为：

由公式（6）可知，朗伯体光源的光亮度与角度无关，因此对于朗伯体光源亮度的描述可直接用平均光亮度。激光照明中，对于单面发光的朗伯体光源，经过对各发射角度的积分，其亮度公式可简化为：

激光照明中很多光源为非朗伯体，对该类型光源的光亮度进行描述时就需要限定观测方向。值得注意的是，在一些实际工程应用中，如显示器，默认的是垂直于发光面方向的光亮度。

以面发射的LED 为例，描述光源[31]性质的物理量可如图4 所示。

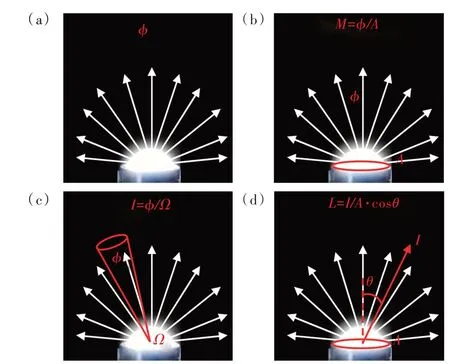
图4 （a）光通量；（b）光出射度；（c）发光强度；（d）光亮度。Ω 是立体角；A 是发光面积；I 是发光强度［31］。Fig.4 （a）Luminous flux（Φ）.（b）Luminous exitance（M）.（c）Luminous intensity（I）.（d）Luminance（L）.Ω is the solid angle.A is the emitting area.I is the luminous intensity［31］.

2.4 光照度和ANSI lumen

光源的一个重要用途是照明，在不同场景下照明都有一定的标准，而照明标准是根据人类的需求和所处环境来制定的，需要考虑灯光的光照度值是否在人类视觉能力需要的光照度值范围内[32]。光照度（Illuminance）为光源投射在物体表面单位面积内的光通量，表示被照物体表面被照亮的程度[24]，单位是勒克斯（lx=lm/m2）。例如，起居室光照度一般要求在100 lx 左右[33]；而一些需要集中精力的环境，如学生自习阅读室、办公室等区域对灯光照度的需求微高，其照度值一般是300 lx 左右[34-35]。因为灯的光照度会影响室内环境亮度、色彩纹理等，较高的光照度可能会对人的情绪和生理造成伤害，而较低的光照度很容易出现眼疲劳、注意力不集中或情绪低迷等问题。

光照度主要受到光源光通量和光束到物体接收面之间距离的影响，还会受到周围环境的影响，如其他光源、温度、空气质量等[36]。所以同一光源下，不同物体表面的照度是不一样的。在均匀照明情况下，平均光照度E的公式可表示为：

ANSI[37-39]（American national standards institute,ANSI）流明与光照度关系密切，即光照度乘投影仪的投影屏幕面积等于ANSI 流明值。在投影仪的实际使用中，不能单纯地比较流明，因为流明只是代表投影仪里光源的光通量，而实际上光源发出的光会先经过多棱镜、DMD 芯片等多个部件[40]，最后经过投影镜头投射到屏幕上，如图5 所示。在整个过程中存在光衰减，不同投影机的光效率不同，亮度衰减程度也就不相同。所以光照度也不能完全体现屏幕被照射的情况，而ANSI 流明是由美国国家标准化协会制定测量投影仪输出光通量的方法[37]，是在一定距离下投影镜头投影到固定面积内的光通量。使用ANSI lumen 可以在测量传统投影仪时获得更加客观的亮度结果，因此大多数投影仪生产商都使用ANSI lumen 作为市场标准亮度单位[38]。

图5 DLP 投影仪结构示意图Fig.5 Schematic diagram of DLP projector structure

对于给定的投影仪，投影屏幕面积越大，且投影镜头到屏幕的距离越远，则屏幕上的照度就越小[37]，该照度与光照度本质相同，它是固定面积上的光通量。ANSI lumen 的测量方法：将屏幕画田字状，分成九份相等面积的方格，分别测量九个方格中心点的照度值，取平均照度值（九点照度值平均数据处理）后再乘以屏幕总面积可得ANSI lumen 值[38,40]。

投影仪除了常用的ANSI lumen 之外，其输出光通量还有ISO（International organization for standardization,ISO）流明[38]和CVIA（China video industry association,CVIA）流明[39]等。其中ISO lumen 与ANSI lumen 测试方法不同，因为ANSI lumen 在测试时通常会有选择性地忽略投影镜头到屏幕距离和这期间的光损耗。ISO lumen 受ISO 监管，要比ANSI lumen 严格很多。假如固定投影仪亮度，则ANSI lumen 的值比ISO lumen 大，两者之间的转换比是1∶0.8。CVIA lumen 是由中国电子视像协会（简称CVIA）于今年主导颁发的，适用于各类投影仪，CVIA lumen 测试指标增加了色温、色差等光学参数，弥补了传统标准存在的漏洞。ANSI lumen 只适用于传统的投影仪，已经不适合国内主流投影仪产品[39]。值得注意的是，一些研究将单管小功率激光器聚焦在数十微米甚至数微米内，激发材料可产生数百流明的光，光亮度可达上百万坎德拉/平方米。但是，该超高光亮度数值对器件开发的实际意义并不大。例如，对于投影设备而言，光源需要兼具高光通量和高光亮度，才可以获得高的ANSI lumen 值。因此，在实际工程开发中，需要结合多个光度学指标综合考虑。

2.5 光度学参数汇总分析

基于上述内容，光度学参数的相关概念总结于表1。当发光表面均匀时，光通量除以立体角可得到发光强度；发光强度除以投影面积可得到光亮度；而光通量除以发光面积可得到光出射度。在光度学参数中，光通量、发光强度和光出射度都是用于描述发光体的物理量；而光照度则是用于描述被照明物体的物理量，它是由光通量除以被照物体的面积得到的[24]。

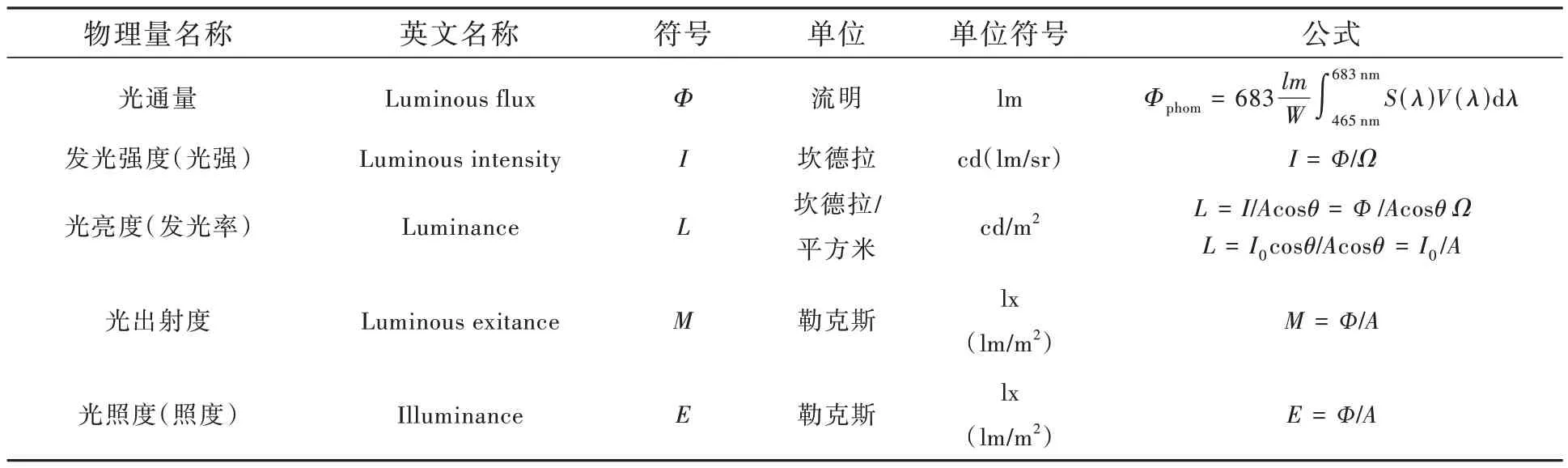
表1 光度学参数的相关概念［24］Tab.1 Concepts related to photometric parameters［24］

3 光度学参数在激光照明中的使用

得益于其成熟的封装技术，LED 产业中获得光度学参数的方法主要是将材料封装成所需光源，然后通过“积分球-分光光度计”系统进行测试。由于LED 光源仅有一种主流的封装模式，即透射式封装，结合LED 本身的朗伯体发光特性，使得LED 的测试方案也比较固定。对于激光照明而言，封装模式分为透射式和反射式两种，对应的材料测试方案自然也分为透射式和反射式，如图6 所示[41]。透射模式封装方案激光照明器件更加紧凑，但对荧光材料的透过率和热导率要求较高。在样品测试和封装时，反射模式相对透射模式较复杂。反射模式最突出的优点是激光辐射点或发热点靠近热沉，散热较好，可以获得相对较高的（热）饱和阈值。该特性有助于光源器件取得较高的饱和阈值和峰值亮度。此外，反射模式在实际应用中，光的有效利用率更好，所以往往呈现出更高的效率[42-43]。因此，测试模式对于材料的性能测试会带来较大影响。

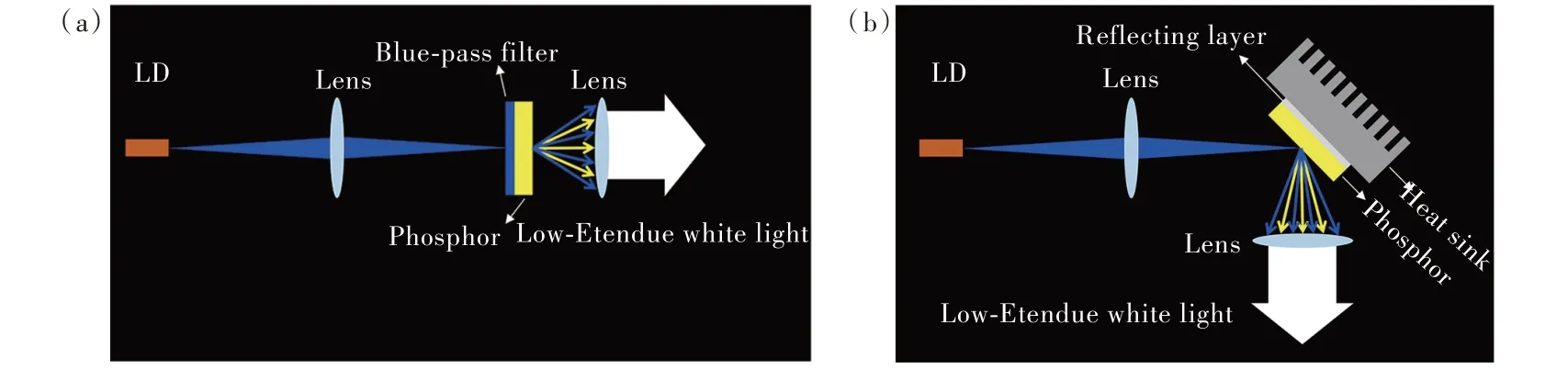
图6 荧光转换器示意图。（a）透射模式；（b）反射模式［41］。Fig.6 Schematic structure of the pc-wLD in transmission mode（a）and reflection mode（b）［41］

3.1 光通量、流明效率和饱和阈值

通常测试会获得横坐标为波长、纵坐标为单位步长光功率（W/nm）的光谱，即光功率分布函数，结合视见函数利用公式（1）进行积分，可获得对应发光材料的光通量，测试设备如图7 所示[41]。获得的光通量除以对应激发激光器的输出光功率，称为材料的流明效率[9]（Luminous efficacy），单位是lm/W。值得注意的是，此处的流明效率指的是“光-光”流明效率（又称辐射发光效率），而LED工业中常用的“电-光”流明效率（Wall-plug luminous efficacy，又称电源发光效率）则需要用光通量除以电源的输出电功率。“电-光”流明效率会涉及到激光器的驱动电路、激光器效率等因素，而对于材料学研究，“光-光”流明效率是更加直观的指标。随着激光功率不断上升，荧光材料在峰值光通量对应的激光功率（或功率密度）是评估该材料在激光照明领域应用前景的基础数据，即饱和阈值（Saturation threshold）[43]。饱和阈值可分为光饱和阈值和热饱和阈值[43]。

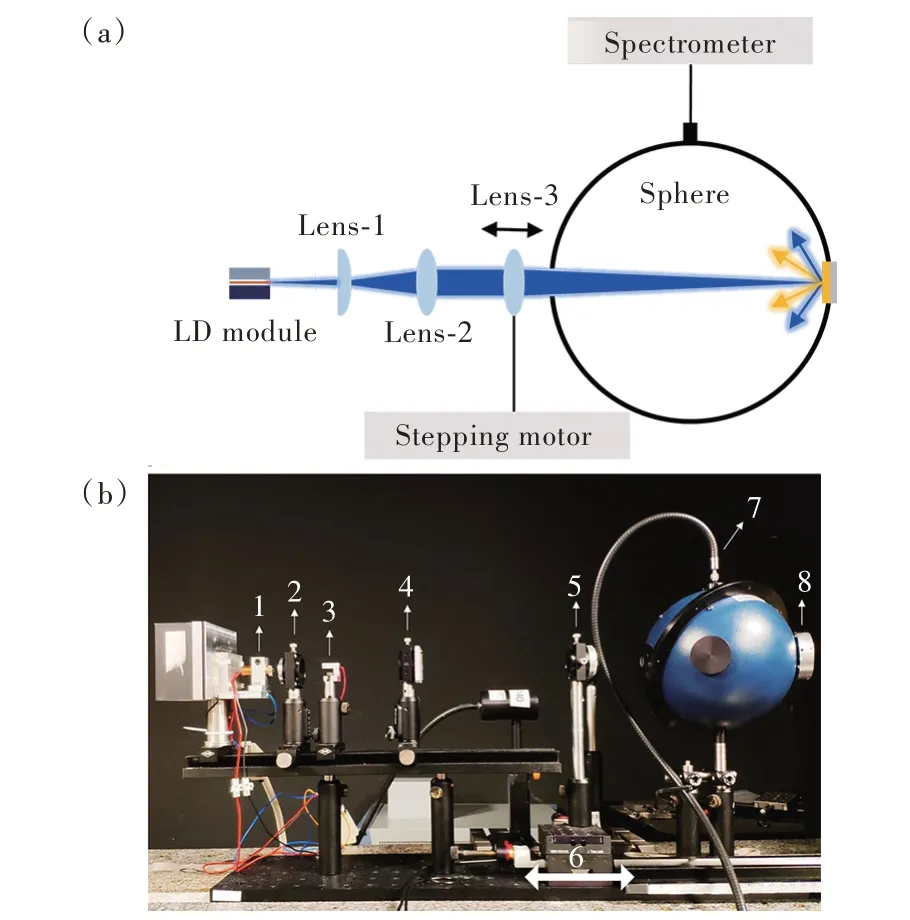
图7 （a）光通量和发光饱和度测量系统方案；（b）材料测试设备图像［41］。Fig.7 （a）Scheme of the luminous flux and luminescence saturation measurement system.（b）Material testing equipment diagram［41］.

值得注意的是，照明和材料产业对于“efficacy”的翻译主要是“效率”。但在实际应用的绝大多数场景中，效率应该是百分比，对应的是“efficiency”，例如机械效率、热效率、量子效率[44]等。所以“efficacy”更加达意的翻译应该是“效能”，意味着存在单位的转换。照明行业中有少量的报道采用“光视效能”来翻译“Luminous efficacy”。在此，笔者倡议在中文描述中应采用更加准确的“流明效能”或“发光效能”来代替“流明效率”。

3.2 光出射度和激光功率密度

如果仅以光通量来描述两款光源，无法全面地评估它们的性能优劣。例如，荧光灯相对于激光光源发光面积大，所以相等光通量条件下激光光源固然要比荧光灯的光出射度大。

准确测量材料发光光斑的大小是获得材料光出射度的关键。对于光强满足高斯分布的激光光束，当光强降至中心光强1/e2时，其位置到中心点距离的两倍，定义为激光光斑大小[18,31,41,45]，如图8（a）所示。其中，0 处指光束中心的峰值辐照度，W是激光光束的半径。根据激光光斑的大小可以获得激光功率密度。发光光斑的大小也可以类似定义。值得注意的是，当激光激发荧光材料时，实际发光的光斑直径往往明显大于激光光斑。图8（b）所示的发光光斑的亮度对应于光的强度，在实际测量中，激光光束的强度分布可能不是规则的高斯分布，如图8（c）所示，因此光斑直径的准确测量取决于光斑中心强度的确定。测量光斑大小的装置如图8（d）所示，激光光源为一个单管LD，激光光束经聚焦系统汇聚后照射到荧光材料上，通过调节聚焦系统，可以调整照射在荧光材料上的激光光斑大小（＜40 µm）。利用4f 成像系统在CMOS 相机中可获得荧光材料上光斑的像，为了防止强光饱和CMOS，相机镜头前可放置等比例衰减滤光片[31]。在荧光材料与相机之间放置多组滤光片，通过切换滤光片实现对激光光斑和荧光光斑分别成像，通过分析光斑的像图可精确获得光斑直径。符合朗伯体发射的发光材料的光出射度（Luminous exitance）便可以用公式（2）进行计算获得。

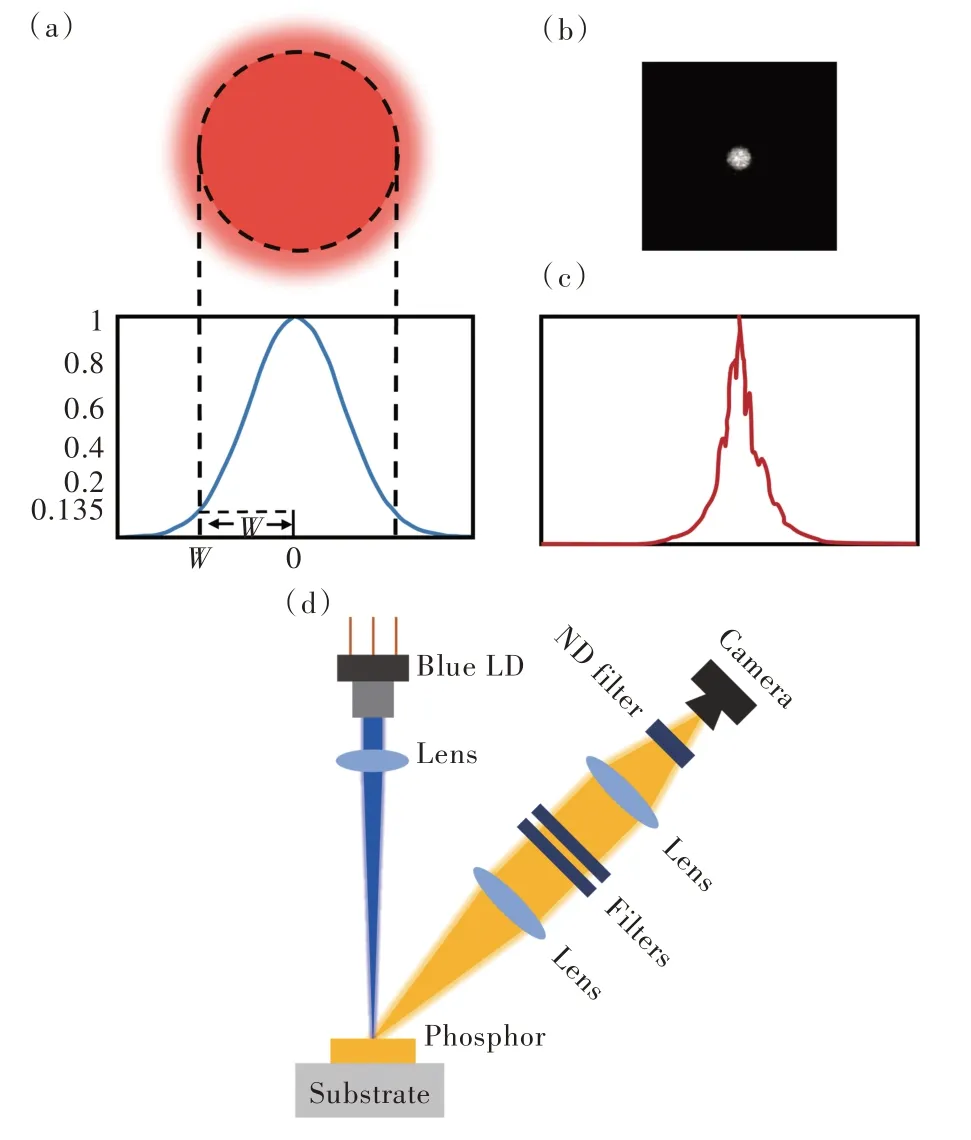
图8 （a）激光光斑的高斯截面图；（b）测量的发光点图像；（c）相应的截面强度分布；（d）发光光斑直径的测量装置［18，31，45］。做了清晰化处理。Fig.8 （a）Illustration of Gaussian cross section for a laser spot.（b）Measured luminescence spot image.（c）The corresponding cross-section intensity distribution.（d）The measurement setups for luminescence spot size［18，31，45］.Clarity has been made.

3.3 光亮度的使用

光出射度只能表征光源表面单位面积光通量的多少，它不考虑辐射方向，所以不能全面描述发光物体的发光特性，此时就需要另一个物理量——光亮度（Luminance）来表征发光物体在不同方向的辐射特性[24]。光亮度是光源发光强度与光源发光面积的比值，即光源单位投影面积上的发光强度（发光面的明亮程度），是人眼对光源发光强度的主观感受。激光照明主要是单面发光，即只在荧光材料的一面发光，包括透射式和反射式两种光源[41]。

例如，在对激光诱导单晶YAG∶Ce 荧光粉发光饱和的研究中[41]，当激光功率为3.38 W 时，实现了465 lm 的光通量；而后在对该单晶进行光斑的研究中[45]，激光光斑直径为390 µm 时，由图8 所示设备测得发光光斑直径为405 µm。由此可计算出发光光斑面积约为0.129 mm2；激光照明主要是单面发光，由公式（2）代入数据可计算出光出射度约为3 604 lm/mm2；在理想情况下，光出射度除以π 即得光亮度，约1 100 cd/mm2。

4 总结

光度学是以人眼视觉感受为出发点、引入视见函数来评估和度量可见光的一门学科。本文的主要目的是向荧光材料领域系统地介绍“光强”、“光出射度”、“光亮度”、“光照度”等参数在内的光度学基础知识，以帮助研究者全面评估照明器件的光学性能；并在此基础上，建立基于光度学物理量来优化材料设计的策略。例如，高饱和阈值并不一定意味着高亮度，因为它还涉及到光谱的分布、光斑的扩展和光分布等因素。综上，通过对光度学物理量的系统梳理，将有助于科研工作者设计和开发性能更加优异的发光材料，进而推动照明行业的持续发展。

最后，笔者建议在固态照明用荧光材料的性能设计和表征中，不应只注重单一光度学参数指标，需要多指标结合考虑。例如，描述饱和阈值时，建议将功率和功率密度相结合；描述流明效率时（尤其对于红色荧光材料），需要结合转换效率；描述光亮度时，需要结合总光通量。对于不同应用，LED场景下，流明效能（Luminous efficacy）相对重要；LD 场景下，光亮度（Luminance）和光出射度（Luminous exitance）相对更为重要。上述有针对性的多维度的研究思想可以更准确地评估材料的应用前景，进而更好地指导器件开发，推动相关产业发展。

本文专家审稿意见及作者回复内容的下载地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20230166.