直升机涡环状态边界风洞试验研究

2023-12-04王畅马帅黄志银王浩文黄志远邓皓轩

实验流体力学 2023年5期

王畅，马帅，黄志银，王浩文，黄志远,*，邓皓轩

1.清华大学航天航空学院，北京 100084

2.中国空气动力研究与发展中心低速空气动力研究所，绵阳 621000

0 引言

直升机具有低空机动性好、部署灵活度高、受地理空间限制较少等特点，已成为纵深渗透、战场机降、垂直登陆、物资运输、搜索营救等特种任务中不可或缺的重要航空装备。垂直起降和短距起降是直升机的特长之一，可以使直升机展开任务时不受地形条件制约。然而，直升机在下降飞行中存在进入涡环状态（vortex king stale,VRS）的隐患[1]，影响直升机飞行安全。

涡环状态发生在直升机垂直下降或小前飞速度下降阶段，是相对来流挤压旋翼尾流导致旋翼空气动力性能改变的一种特殊气动现象。直升机进入涡环状态后，飞行特性通常表现为自主性加速下坠、振动加剧、总距操纵失效[2]，若缺乏足够离地高度和有效处置，直升机可能坠毁。不同构型和吨位的直升机均发生过涡环状态事故，如V-22 倾转旋翼机2000年在美国坠毁[3]，R66 轻型直升机2016年在中国（黑龙江）坠江，Bell 412 中型直升机于2003 和2012年分别在瑞典[4]和日本[5]坠毁，AS332 中型直升机于2013[6]和2020[7]年在法国坠毁，Mi–8T 大型直升机2008 和2014年分别在中国（内蒙古）和俄罗斯[8]发生事故，Mi–26T 重型直升机2018年在俄罗斯坠毁[9]。此外，尾桨在遭遇与其尾流方向相反的来流干扰时，也会因类似原因产生尾桨涡环状态[10]，我国某型直升机2018年和2019年连续发生了2 起因尾桨涡环状态导致的坠机事故[11]。

避免直升机涡环状态事故的前提是准确划定旋翼涡环状态边界，即确定旋翼涡环状态发生和消失时的临界飞行速度，指导飞行员避免操纵直升机进入该速度区域[1]。随着航电技术的发展，H160 等新型直升机搭载了涡环状态自动预警和干预系统[12]，旋翼涡环状态边界模块是该系统的重要组成部分。

截至目前，各国航空研究机构制定的旋翼涡环状态边界已有数十种[13]，其中高-辛边界[14-16]、ONERA边界[17-18]、NASA[19-20]边界（图1，VX为飞行速度沿旋翼桨盘的分量；VY为飞行速度沿旋翼轴的分量，向下飞行为负；vh为旋翼等效悬停诱导速度。）已在险情防范和事故分析中广泛应用。这3 种边界不仅在临界速度上不尽相同，对许用下降率随前飞速度变化的判断也有着相反观点。在实际应用中，对涡环状态边界的分析和各种涡环状态边界的差异困扰着人们对飞行特情的预判及防范对策的导向。

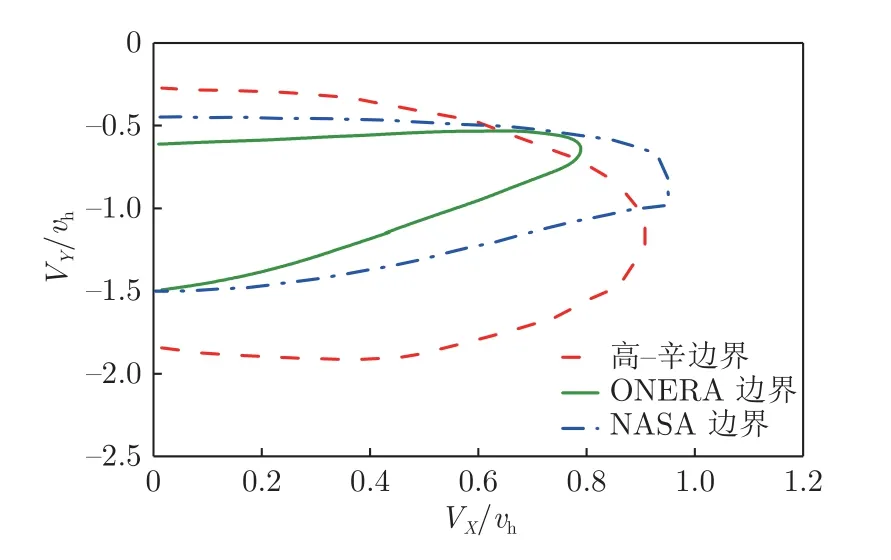
图1 3 种涡环状态边界对比Fig.1 Comparison of three kinds of vortex ring state boundaries commonly used in Engineering

涡环状态边界在特情防范对策判定[21-23]、预警系统开发[24-30]、事故原因分析[4-9]等领域已经得到较多关注。相比之下，关于各类边界的划定原理、偏差原因和适用范围的深入探讨较少。虽然研究者对涡环状态下的旋翼气动机理已逐步达成了共识[31-35]，但鲜有研究从事故预防角度对风险关联物理机制进行考量。在现代战争突发性、快速性、立体性和破坏性增强的趋势下，对直升机的快速部署能力和战场生存能力提出了更高要求，下降飞行快速机动性能的重要性更加突出，涡环状态边界存疑使得预防风险和积极发挥机动性能之间的矛盾更加凸显。在这种形势下，一方面要加强对涡环状态风险因素、边界功能、气动机理、各边界差异本质原因等的深入理解，以免对涡环边界机械应用；另一方面，亟须发展与风险防范需求相契合且具有较高置信度的边界模型。

基于以上背景，为加深对涡环边界特情发生机制的认识和加强事故预防，本文着眼于涡环状态边界在风险预防中的实际指示功能，探讨其界定准则、物理机制和量化表征；回顾各类边界的起源，讨论其适用范围和局限性；设计并实施相关风洞试验，建立半经验化涡环状态边界预测模型。

1 涡环状态风险因素与飞行力学机制

对涡环状态的内涵进行科学准确的解读是本文研究工作的起点。目前国际上尚未对涡环状态形成明晰、可量化的定义。“涡环状态”一词最初由De Bothezat[36]于20世纪初提出，用以表征下降飞行时向上穿过旋翼的自由来流与向下的尾流相互作用而形成的环形流动现象。该现象在美国《海军航空器训练与操纵规范》[37]中被称为“功率沉陷”（power settling），指需用功率超过直升机额定功率的情况。美国《陆军飞行基础》[38]及FAA（Federal Aviation Administration）在2012年之前出版的《直升机飞行手册》[39]中使用了“带功率下沉”（settling with power）的术语，即：尽管使用了全部可用功率，直升机仍保持下降。目前，各机构倾向于统一使用“涡环状态”这一术语。加拿大交通部于2006年将“带功率下沉”从《直升机飞行训练手册》[40]中删除；FAA 新修订的《直升机飞行手册》[41]中单独使用了“涡环状态”一词，其定义为“直升机以20%～100%的可用功率垂直下降且爬升能力很小或丧失的空气动力学状态”。

以上术语从不同角度对涡环状态进行了定义，但从事故预防角度而言，涡环状态应是由环状旋涡流动结构所导致的某种风险，涡环状态边界则指示了这种风险发生的范围。为此，首先须明确这种风险的表现形式，人们在事故预防实践中希望风险边界具备何种功能，以及如何依据这种功能对风险进行确定和划分。

本节通过研究若干起涡环状态事故的调查报告，辨别导致事故的风险因素，从实用性视角在现象层面界定涡环状态边界；通过综述国内外直升机涡环状态飞行试验研究成果，梳理直升机穿越涡环状态的飞行操纵与响应特征，探究与风险相关的飞行动力学机制。

1.1 涡环状态风险因素与边界功能分析

1.1.1 涡环状态飞行事故调研

研究了引言中列举的6 起事故的官方调查报告[4-9]，因这些事故原因大多类似，仅介绍其中2 例。

案例1[5]：2003年3月25日，瑞典国防军一架Bell 412 中型直升机在结冰湖面地区开展医疗救援科目训练，在第9 个架次着陆过程中，直升机以很高的下降速度坠毁。

事故调查委员会还原的飞行数据记录仪显示：事故架次从零前飞速度至坠地仅用时11 s，而常规操纵流程耗时约31～61 s。坠地前3 s，直升机下降速度已超过-0.75vh，1 s 后机组才意识到直升机下降速度过大而采取拉起措施，但此时离地仅20 m，未能成功处置险情。该事故主要原因是飞行员的注意力分散，在意识到直升机下降速度过高而进入涡环状态前一直在减小旋翼总距。

案例2[8]：2014年9月4日，俄罗斯一架Mi–8T直升机在机场着陆过程中高速撞击地面，侧面副油箱破裂引起火灾。

根据俄罗斯国家间航空委员会的调查：在坠地前7 s，直升机离地高度仅为50 m 且垂直下降速度超过-8 m/s，此时飞行员将旋翼总距从7.5°提升至10°，旋翼转速降低至原来的88.9%；而后飞行员进一步提升了总距，直升机以6°俯仰角姿态垂直下坠，与地面撞击前的下降速度约为-5.5 m/s。该事故主要原因是直升机在后飞转入降落的减速过程中进入了涡环状态：一方面，机体俯仰角急剧变化至-12.5°，导致垂直于旋翼桨盘向上的气流分量显著增加；另一方面，在此过程中，旋翼的总距过低，比悬停时低3°，最终导致了事故的发生。

1.1.2 涡环状态事故表现形式与边界功能分析

以上案例中，事故由突然加剧且难以通过提升总距来阻止的下降运动所触发，而振动加剧等现象并非事故直接原因。从预防坠机事故的目的出发，应以前者为关键风险界定直升机进入涡环状态。

在较高空域中，当直升机在快速下降等科目中进入涡环状态时，需以直升机运动重新稳定、旋翼升力和操纵性能恢复的临界速度为参考，判断是否有足够离地高度使直升机穿越涡环状态。从预判离开涡环状态的目的出发，应以关键风险解除界定直升机退出涡环状态。

1.2 直升机涡环状态飞行特性

1.2.1 浮沉运动速度不稳定性

Reeder 和Gustafson[42]对Sikorsky R4 直升机开展了垂直下降状态的飞行试验，结果发现：下降速度>-2.54 m/s 后，直升机的下降率非指令性急剧增大，反映了浮沉运动速度的负阻尼态；下降速度>-7.62 m/s 后，可以操纵直升机保持稳定的下降飞行速度和姿态。

Taghizad 等[18]使用CEV（法国飞行试验中心）Dolphin 6075（简称D6075）直升机开展了下降状态的飞行试验，这是目前公开文献中数据最全的直升机涡环状态飞行测试项目。试验采取图2所示的前飞速度恒定、逐步增大下降速度的方式使直升机进入涡环状态。图3 为试验总距操纵与速度响应的时间历程。从图3 可以看出，随着下降速度增大，浮沉运动稳定特性的变化分为3 个区间：从下降速度为0 的初始时刻起，随着总距小幅递减，下降速度略增，并在约6 s 内趋近匀速，体现出速度稳定性；t≈85 s，下降速度增至约-5 m/s，此后20 s 内，在同等量级的总距激励下，下降速度大幅度增大；t≈105 s后，直升机经历速度过冲后以约-15 m/s 的下降速度维持匀速下降运动。Taghizad 等将上述过程中下降速度出现突增和恢复匀速时的临界飞行速度分别标记为进入和离开涡环状态的边界速度。

图2 CEV 增大下降速度进入涡环状态的试飞方式[18]Fig.2 Flight test mode with increasing descent speed to enter vortex ring state applied by CEV[18]

图3 穿越涡环状态过程中总距、前飞速度、下降速度的时间历程[18]Fig.3 Time history of collective pitch,forward flight speed and descent speed during vortex ring state[18]

1.2.2 振动特性

在Reeder 和 Gustafson[42]开展的Sikorsky R-4直升机垂直下降飞行试验中，下降速度>-2.54 m/s后，直升机除垂向飞行速度失稳外，还伴随着滚转运动和较强的偏航摆动。

陆洋等[34]使用R22 直升机开展了涡环状态边界的飞行试验，发现机头开始出现航向摆动是直升机进入涡环状态的首要特征，飞行实测的临界垂直下降速度为-0.39vh。

D6075 直升机以下降速度恒定、前飞速度逐步降低的方式（图4）进入涡环状态时，未出现直升机下降速度突增的现象。图5 为水平速度约7.7 m/s 的平直飞行与涡环状态下3 个轴向操纵的加速度时间历程对比。在涡环状态下，俯仰、滚转与偏航姿态表现出大幅度振荡，即使施加往复修正操纵，机体仍具有较大的加速度和角加速度。需要注意的是，直升机以图2 的飞行方式进入涡环状态后同样出现了较大幅度的振动，但飞行员未能在下降率突增的过程中稳定直升机飞行高度，从而未能开展上述操纵修正飞行姿态。Taghizad 等将振动显著增大的飞行速度标记为直升机进入涡环状态的侧向边界速度[18]。

图4 CEV 降低前飞速度进入涡环状态的试飞方式[18]Fig.4 Flight test mode with reducing forward speed to enter vortex ring state applied by CEV[18]

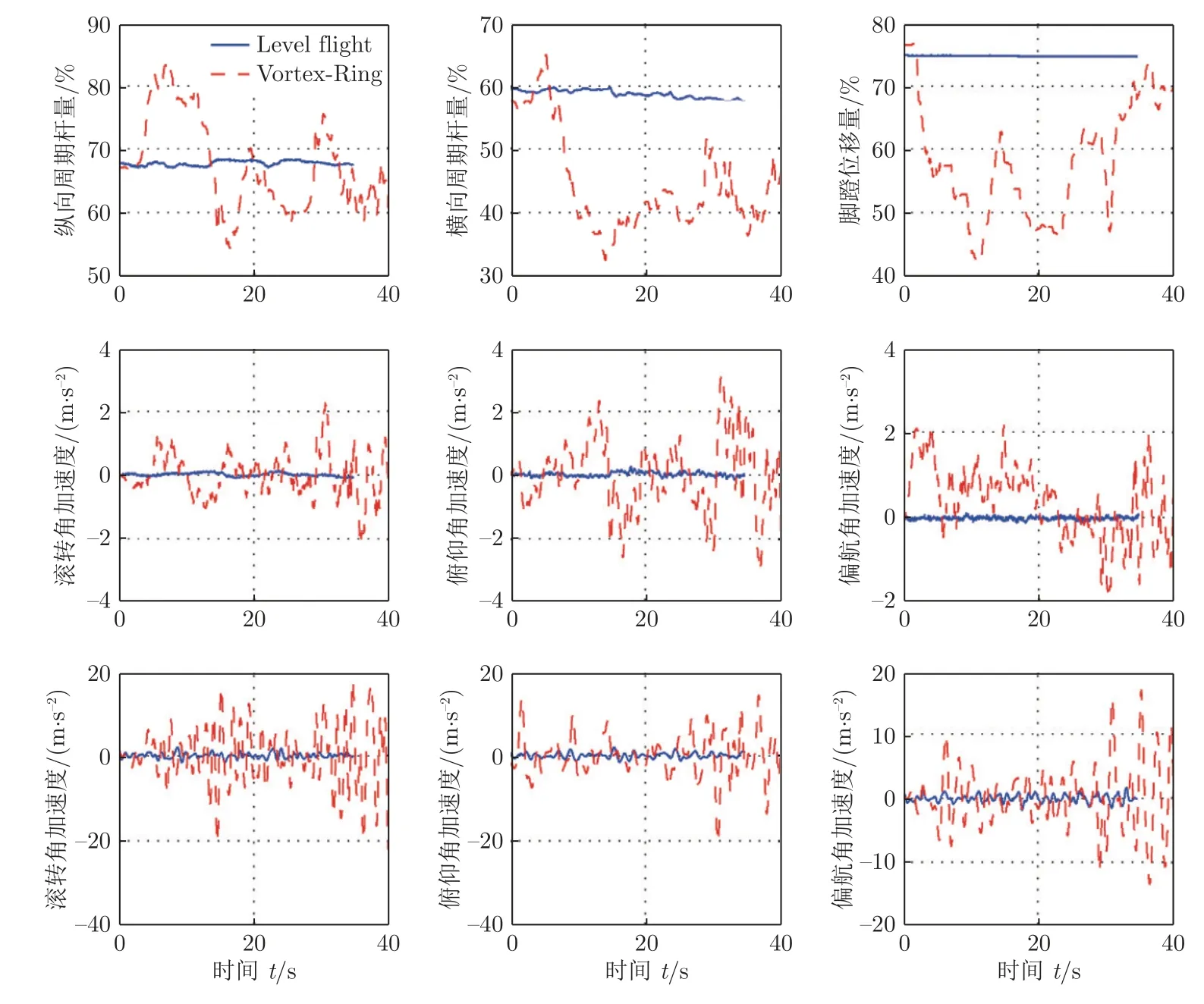
图5 平直前飞与涡环状态下操纵与加速度时间历程对比[18]Fig.5 Comparison of control and acceleration time history when entering vortex ring state[18]

Stewart[43]对Sikorsky R–4B、R–6、S–51，Bell 47 和Bristol 171 等5 种机型开展了飞行试验，对比了它们在-2.54～-7.62 m/s 垂直下降速度区间的飞行特性。Sikorsky R–4B 表现出的失控程度和沿俯仰、滚转、偏航方向的振动最为剧烈；Sikorsky S–51 的滚转振动较为剧烈，但偏航方向的振幅非常小；Bell 47 在偏航方向的振动较为剧烈，但可保持较稳定的俯仰姿态；Sikorsky R–6 和Bristol 171 在测试速度区间内表现出比其他直升机更低的振动幅度。

从以上飞行实测结果可以看出：在涡环状态下，各类机型直升机的振动方向和振动程度表现出较大差异，采用振动值表征量化直升机涡环状态边界在应用中可能存在普适性问题。

1.2.3 对总距操纵的响应

在Stewart[43]开展的各类机型直升机垂直下降飞行对比试验中，大部分直升机进入涡环状态后对总距操纵不敏感，仅有Sikorsky R–6 和Bristol 171能通过提升总距获得上升速度。

CEV[18]开展的飞行试验中，也对D6075 直升机进入涡环状态后的总距操纵进行了测试。图6 为涡环状态下飞行员提升总距后直升机响应的时间历程：飞行员在t≈15 s 时小幅度提升总距，未能改变直升机下降速度增大的趋势，而在t≈20 s 时增大前飞速度，使直升机的下降速度减小。

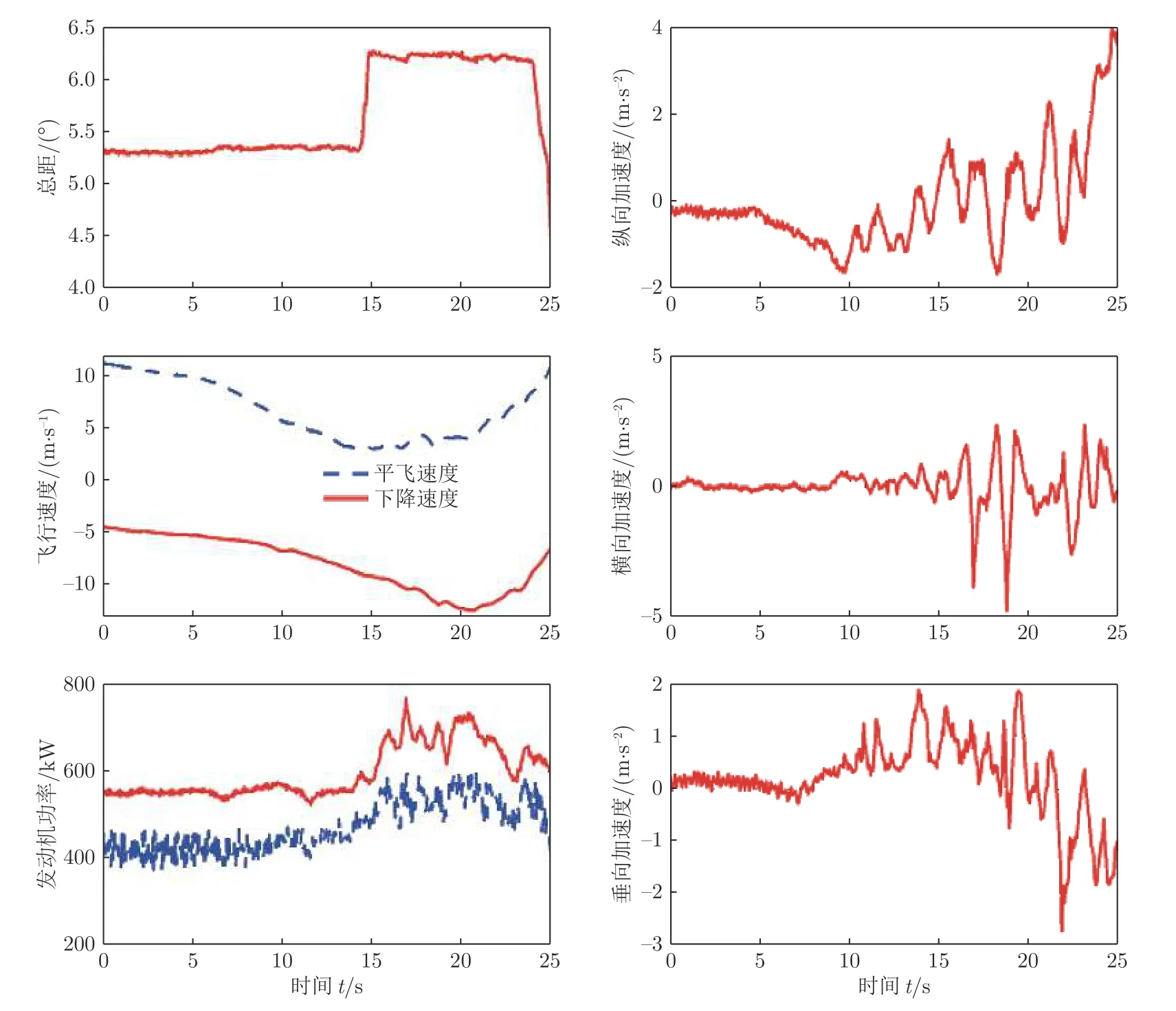
图6 涡环状态下直升机对总距提升的响应[18]Fig.6 Response of helicopter to collective pitch increase in vortex ring state

1.2.4 涡环状态边界的飞行动力学机制

前文关于直升机下降阶段操稳特性的飞行试验研究表明：涡环状态事故发生的实质是下降速度的负反馈调节机制失效、直升机浮沉运动速度失稳。浮沉方向速度阻尼是直升机进入涡环状态的重要判断指标。

涡环状态风险消除后，直升机在更大下降速度下恢复了平衡状态。判断是否退出涡环状态，需综合考虑直升机平衡性、稳定性的恢复情况。

2 涡环状态旋翼气动性能特性与流动机理

在确定涡环状态边界的飞行动力学机制及关键影响因素后，如何构建进入、退出涡环状态与飞行速度的对应关系？这需要进一步从旋翼气动性能中了解飞行特性的变化原因，识别与涡环状态边界关联的旋翼性能指标，从旋翼流动机理中探究其发生机制，总结飞行速度对其的影响。

2.1 旋翼气动性能特性

涡环状态下旋翼气动性能的量化研究以实验室测试为主。表1 列出了国内外在此方面已开展的主要工作。本节从中选取了垂直下降时，总距恒定、由下降速度导致旋翼拉力和扭矩变化[44]，以及旋翼拉力恒定、由下降速度导致旋翼总距与需用功率变化这2 种情况[45]分析旋翼气动性能与飞行特性的关联。

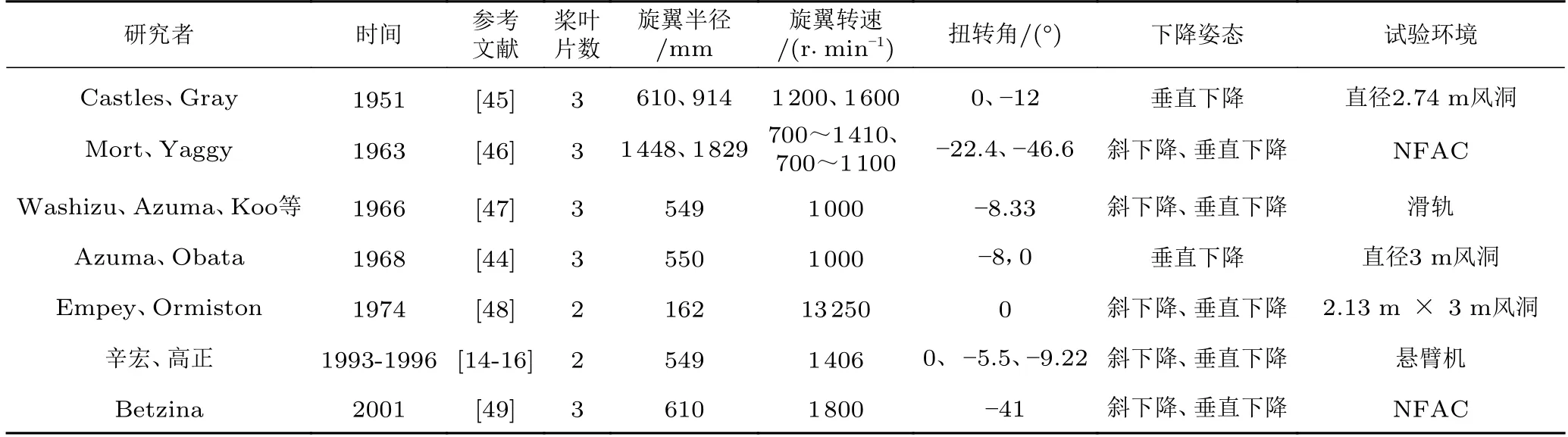
表1 国内外已开展的涡环状态旋翼性能测量试验Table 1 Tests of rotor performance in vortex ring state

图7 为文献[44]中旋翼总距分别固定为8°、10°、12°和14°时，各风速下的旋翼拉力、功率与悬停状态比值曲线。图中，Ct为拉力系数，Cp为功率系数，Ct0和Cp0分别为悬停状态下的拉力系数和功率系数。可以发现：图7（a）中，拉力随风速增大呈现较为显著的增大→降低→增大规律，即旋翼拉力阻尼随下降速度具有正→负→正的变化过程；图7（b）中，功率随风速变化的幅度总体相对较弱。旋翼拉力阻尼决定了直升机浮沉运动速度阻尼，解释了1.2 节中介绍的飞行特征：由悬停进入低速下降时，旋翼拉力具有正阻尼，对应于图3 中t <85 s 前，总距小幅降低后，直升机在不断增大的下降速度中建立平衡的过程；随着下降速度增大，旋翼出现了拉力负阻尼效应，拉力值显著降低，对应于85～105 s 时，飞行员未修正总距的情况下，直升机下降速度突增的过程；下降速度进一步增大后，旋翼拉力阻尼恢复，同时拉力值大幅度增大，解释了t ≥ 105 s 后，直升机在总距不变的情况下以-15 m/s 的下降速度维持稳定飞行的过程。

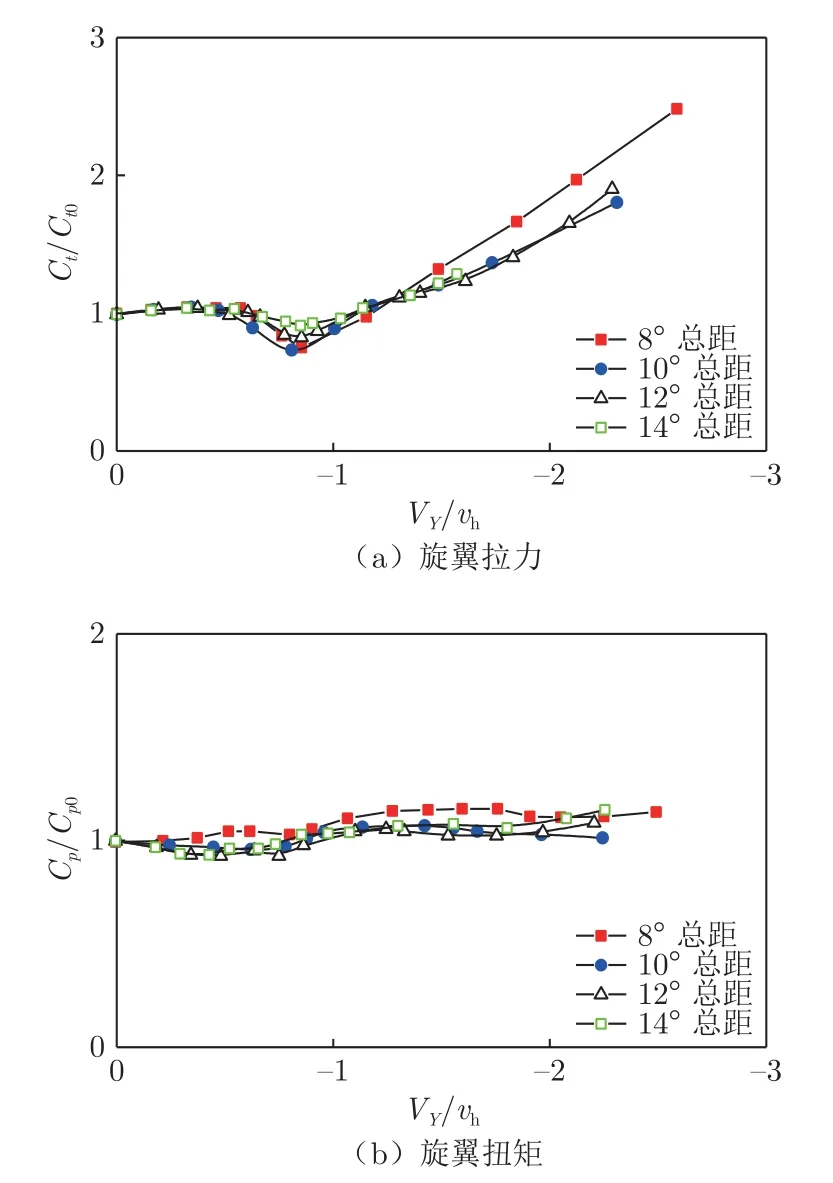
图7 垂直下降状态旋翼拉力和扭矩随等效下降速度变化（总距恒定）[44]Fig.7 Variation of rotor thrust and torque with equivalent descent speed under vertical descent(constant collective pitch control)[44]

图8 为文献[45]总距配平试验中得出的旋翼恒定拉力情况下总距和需用功率随风速的变化，σ为旋翼实度，（Ω·R）为桨尖速度，ΔCp为当前试验状态与悬停零升力状态需用功率的差值。从图中可以看出，在旋翼拉力维持不变时，总距和需用功率随风速变化趋势与图7（a）所示的曲线具有负相关性。由悬停转入低速前飞时，总距和需用功率降低，符合图3 中t≈85 s 前的总距操纵规律。随着下降风速增大，下降速度增大，旋翼总距和需用功率增大，呈现出总距反操纵的特性，符合进入涡环状态后带功率下沉的情况；相应的，总距和需用功率增大至超过悬停状态下的总距和需用功率，符合功率沉陷的特征。随着下降速度进一步增大，总距和需用功率呈现较大幅度的降低，在较大下降速度下已显著低于悬停状态，直升机操纵裕度和功率裕度增大。

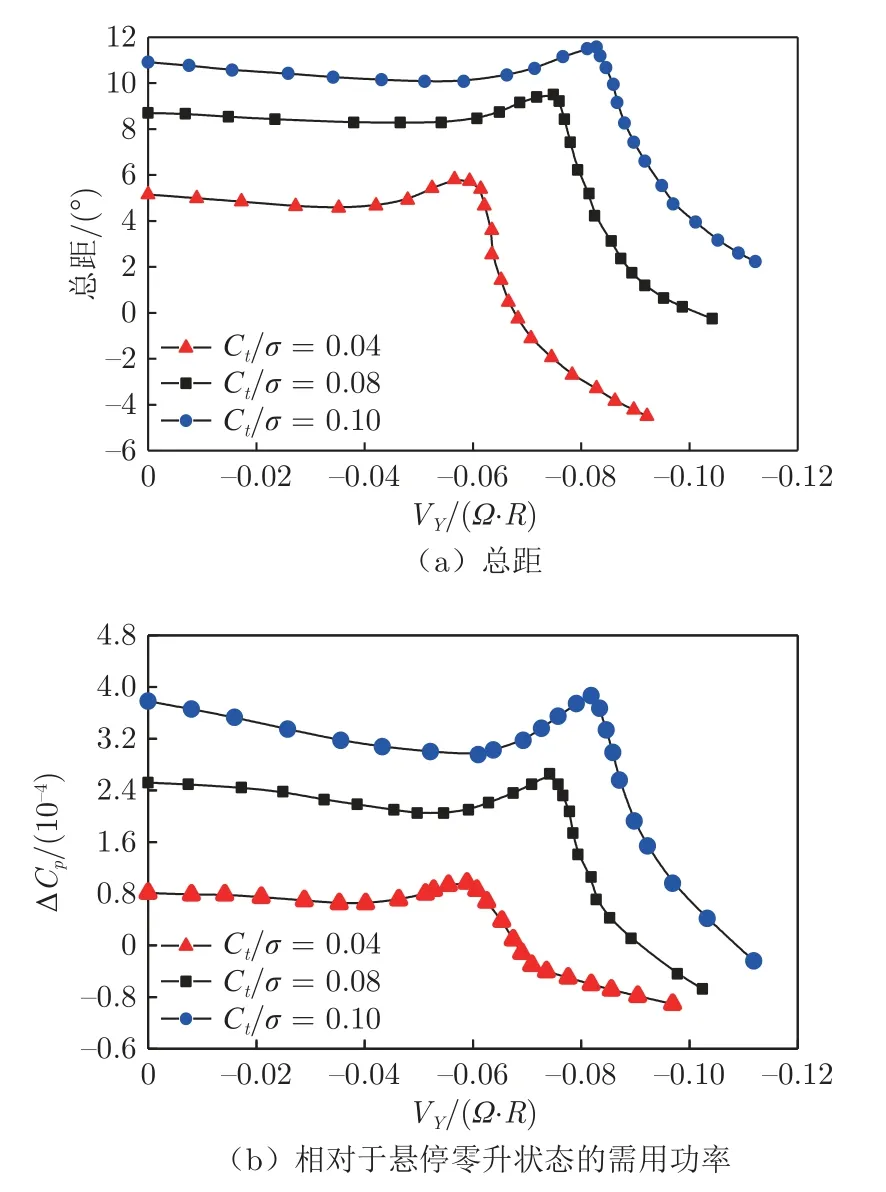
图8 垂直下降阶段旋翼总距和功率随下降速度变化（拉力恒定）[45]Fig.8 Variation of rotor collective pitch and required power with descent rate under vertical descent(constant thrust)[45]

基于以上分析可知，旋翼的拉力负阻尼效应及对应出现的升力损失、需用功率增大诱发并加剧了直升机浮沉运动速度失稳，是造成直升机进入涡环状态的直接原因。

值得注意的是，一些文献以拉力阻尼恢复为正作为直升机退出涡环状态的依据[19,50]，但拉力阻尼恢复为正恰好发生在拉力损失或需用功率最大值处，依旧处于功率沉陷的风险区。因此，本文认为以旋翼总距与悬停状态总距相等时，旋翼拉力在较大下降速度下恢复至悬停拉力（直升机总重）的状况判定直升机退出涡环状态更符合实际。

2.2 桨盘入流特性

旋翼进入涡环状态后性能变化的原因可能有3 种[50]：桨叶失速、桨盘处垂向气流速度为0、桨叶剖面有效迎角降低。随着流场定量测试技术和旋翼流场数值模拟手段的发展，学者对涡环状态下旋翼流动的研究更加深入，桨叶剖面有效迎角降低是导致旋翼进入涡环状态后性能变化的主要原因已被学界普遍接受。

图9 为Johnson[19]综合大量试验数据构造的涡环状态旋翼入流模型，该模型已在涉及涡环状态的飞行仿真中被广泛采纳[51]。图中，纵坐标(Vy+v1)/vh为桨盘轴向入流，v1为桨盘处诱导速度。观察Vx/vh=0 的情况可以看出，与图7（a）和图8 类似，随着下降速度增大，桨盘轴向入流变化也分为3 个阶段：垂直飞行速度降至N 点前，桨盘轴向入流呈减小趋势，使桨叶剖面来流角降低，进而导致翼型的有效迎角增大；在N 点至X 点的过程中，桨盘轴向入流呈增大趋势，与虚线代表的滑流理论结果趋势相反，桨叶剖面来流角随之增大，翼型有效迎角减小，进而破坏了旋翼的拉力阻尼；在X 点之后，轴向入流迅速减小，翼型有效迎角随之增大，旋翼的拉力阻尼和性能恢复。值得注意的是，在拉力恒定时，（VY+v1）表征了旋翼有效功率与诱导功率之和，因此其变化规律与图8 一致。

图9 旋翼在涡环状态的入流模型[19]Fig.9 Inflow model of rotor in vortex ring state[19]

图10 为文献[52]中旋翼总距固定为7.4°时，不同垂直下降速度的流场PIV 测量结果（v 为PIV 处理得到的流场速度），随下降速度增大，旋翼拉力先小幅增大（图10（a）），随后降至最低值（图10（b）），最后恢复至悬停值（图10（c））。可以看出，图10（b）中桨盘入流强度显著高于图10（a），而图10（c）所示的桨盘入流强度相较于图10（b）已显著降低。

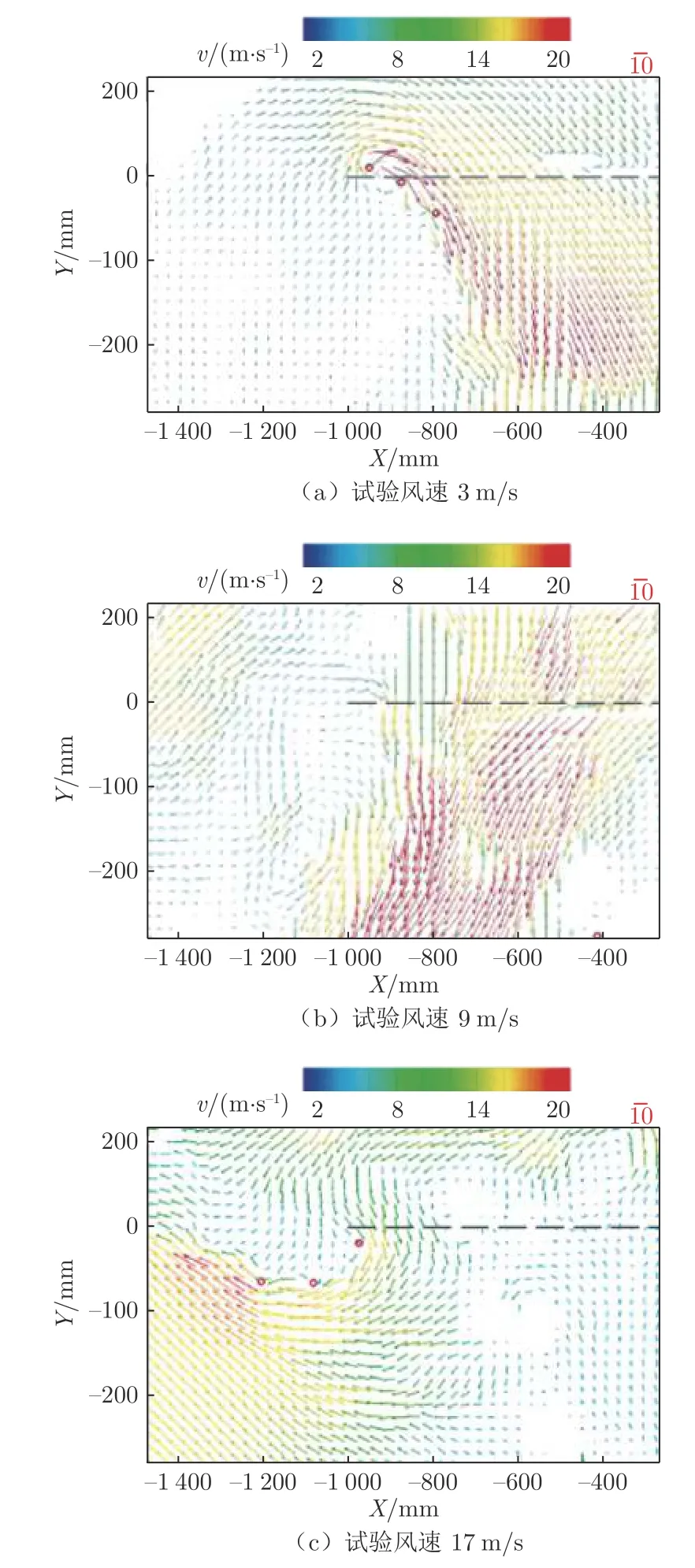
图10 垂直下降状态旋翼剖面速度矢量图[52]Fig.10 velocity vector diagram in vertical descent state[52]

综上所述，在下降飞行阶段，旋翼性能变化方向主要由桨盘轴向入流对桨叶剖面迎角的改变决定，同时，（VY+v1）也表征了旋翼拉力恒定时的需用功率，因而d（VY+v1）/dVY能同时表征旋翼拉力阻尼性质和需用功率的变化情况。

2.3 桨尖涡结构演化机理

在下降速度不断增大的背景下，旋翼桨盘的入流是如何伴随向上增强的相对来流而出现增大趋势的？这需要在桨尖涡空间演化特性中寻找答案。

图11 显示了由Leishman[53]和Brown[54]等通过时间推进自由尾迹计算给出的各飞行阶段下旋翼桨尖涡结构。在下降速度较低时（图11（b）），下游的桨尖涡线在自由来流的作用下被挤压，与悬停状态（图11（a））相比，桨尖涡的轴向结构变得更紧凑且更趋近于旋翼桨盘，同时下游的涡线聚集形成了涡环结构。但这些效应对桨盘处诱导速度的影响有限，不足以抵消自由来流对桨盘入流的减小作用，旋翼入流值仍可保持随下降速度增大而减小的趋势。

图11 下降飞行过程中桨尖涡的结构演化[53-54]Fig.11 Structural evolution of blade tip vortex during descending flight[53-54]

在下降速度达到旋翼进入涡环状态的边界速度时（图11（c）），进入涡环的桨尖涡线数量增多，其空间位置向桨盘传递，该集中涡结构产生的强烈下洗作用逐渐超过自由来流影响，从而占据对旋翼流场的控制优势，桨盘入流因此呈增大趋势。当下降速度增至直升机退出涡环状态时的边界速度（图11（d）），涡环向上运动至桨盘外侧，聚集程度变弱，对桨盘处流动的影响也随之减弱。下降速度进一步增至风车状态时（图11（e）），桨尖涡的运动轨迹趋向上游，且不再聚集。达到一定前飞速度时（图11（f）），桨盘下游聚集形成的集中涡在接近桨盘前即被水平来流吹离。

基于以上分析，桨盘轴向入流变化趋势反映了自由来流与诱导速度对旋翼流场作用的竞争关系。直升机进入涡环状态实质是桨尖涡在旋翼周围聚集，导致诱导速度在桨盘占优的结果。在以上过程中，大尺度集中涡结构的聚集形成、集中涡与桨盘的相对位置关系、集中涡在较高前进比下无法生成等关键因素均由桨尖涡的运动速度决定，而飞行速度是桨尖涡运动的主要驱动力。因此，桨尖涡运动速度对涡环状态边界的表征具有物理意义上的明确指示作用。

3 涡环状态边界研究现状

本节从推导过程、边界因素界定、阈值选取等方面对国内外已发展的涡环状态边界进行梳理回顾，分析总结工程界常用涡环状态边界之间的差异及其适用范围，提出进一步改进的方向。

按照构建方式的不同，本节将涡环状态边界模型分为理论近似模型、使用试验数据修正的半经验化模型和单纯由试验结果统计抽象的经验化模型。

3.1 理论近似涡环状态边界

3.1.1 Wolkovitch 边界

Wolkovitch[55]以桨尖涡沿旋翼轴向运动速度达到阈值作为进入或退出涡环状态的判定条件。

旋翼桨尖涡构成了旋翼内侧入流与自由来流的分界面，假设其运动速度等于旋翼内侧入流与外侧自由来流的平均值（图12）。桨尖涡的垂向运动速度为0 时，进入涡环状态：

图12 Wolkovitch 对桨尖涡运动速度的假设[55]Fig.12 Wolkovitch's hypothesis on the velocity of blade tip vortex[55]

进一步得到进入涡环状态边界的表达式：

退出涡环状态时，假定桨尖涡向上运动，即VY+v1/2为负值。使用式（3）作为进入涡环状态边界的表达式：

与基于滑流假设的动量理论（式（4））联立，即可得到分别满足式（2）和式（3）的进入与退出涡环状态边界。

图13 中以虚线绘制了Wolkovitch 边界，该边界一直延伸至大前进比下，与达到一定前飞速度时不会发生涡环状态的实际情况不符。但在小前进比下，其形态接近Drees 等[56-58]依据旋翼流态划分的涡环状态边界，说明这种理论假设在一定程度上反映了旋翼流动机理，其推导思路被后续许多研究者借鉴。

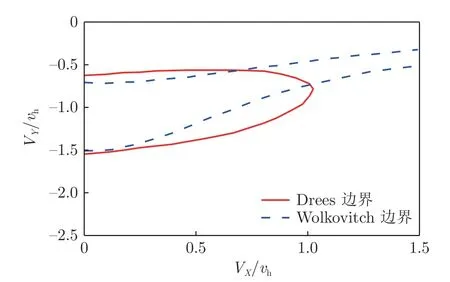
图13 Wolkovitch 与Dress 边界对比[55-56]Fig.13 Comparison of Wolkovitch and Dress boundaries[55-56]

3.1.2 Peters 边界

如图14所示，Peters 等[59]将桨尖涡运动速度假设为自由来流速度在旋翼尾流方向的投影与旋翼尾流速度之和：

图14 Peters 对桨盘处流动的假设[59]Fig.14 Peters′ assumption of flow at the disc[59]

在尝试沿用式（1）和（3）的思路对式（5）构建涡环状态边界未取得封闭后，Peters 借鉴了Gessow等[60]的观点，将进入涡环状态边界的流动判据改为旋翼尾流与自由来流相反：

在退出涡环状态边界的判据方面，沿用式（3）的思路对式（5）设定了阈值：

将式（6）和（7）与动量理论（式（4））联立，得到如图15所示的涡环状态边界。可以看出，在判别式中引入前飞速度项使得边界曲线在VX/vh=0.62 时封闭，该值实际上对应于式（4）中诱导速度不再出现多解的情况。此外，在垂直下降状态一旦有下降速度即进入涡环状态的结论也与事实不符。

图15 Peters 涡环状态边界[59]Fig.15 Peters vortex ring state boundary[59]

3.1.3 Newman 边界

与Wolkovitch 和Peters 使用不同表达式对涡环状态上、下边界分别进行定义不同，Newman[61]使用绝对值相同、方向相反的桨尖涡运动速度阈值表征上、下边界。Newman 认为桨尖涡运动主要由旋翼的尾流驱动，并考虑到桨尖涡聚集主要由轴向速度决定，于是对前飞速度进行加权，建立了涡环状态边界理论判据（式（8））。式（8）与式（4）联立可得到如图16所示的涡环状态边界。

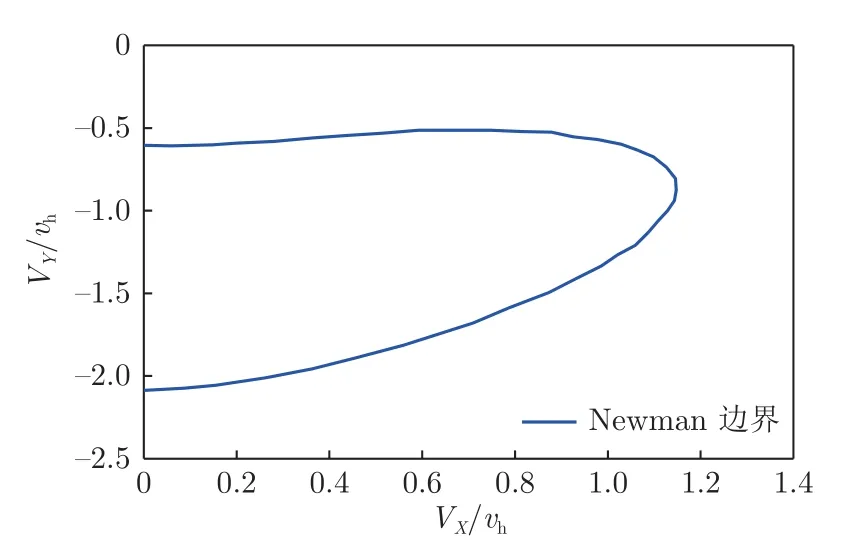
图16 Newman 给出的涡环状态边界[61]Fig.16 State boundary of vortex ring given by Newman[61]

3.2 半经验化涡环状态边界

3.2.1 高-辛边界

南京航空航天大学的高正和辛宏[14-16]使用悬臂机开展了旋翼下降状态模拟试验，发现在总距固定的情况下，时均扭矩在-0.28vh时开始随下降速度增大而增大，由此判断直升机发生功率沉陷。进一步将Peters 判据修改为：当相对来流速度矢量在旋翼尾流速度矢量反方向上的投影超过-0.28vh时，直升机进入涡环状态。式（9）为高–辛涡环状态边界的表达式，与式（4）联立可得出高–辛边界曲线，如图17所示。

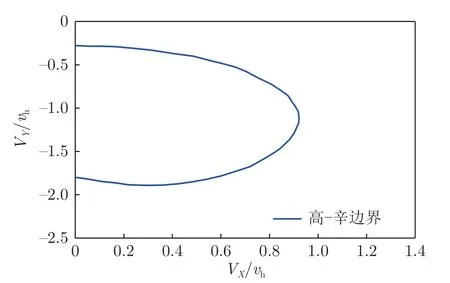
图17 高-辛涡环状态边界[14]Fig.17 Gao-Xin vortex ring state boundary[14]

高正和辛宏是将试验结果引入涡环状态边界半经验模型构建过程的开创者，但仅使用了垂直下降时进入涡环状态的试验数据，且试验中未包含退出涡环状态阶段的模拟。

3.2.2 ONERA 边界

法国宇航院的Taghizad 等[18]认为桨尖涡运动速度应为桨盘内、外侧流动速度的平均值，在Newman 的基础上，建立了涡环状态边界公式：

式中：VX/k 为桨尖涡水平速度，ε为阈值系数。

通过匹配1.2 节CEV 飞行试验的数据，确定k和ε分别为4 和0.2，得到了如图18所示的涡环状态边界。在ONERA 边界的构建中，式（10）须与Taghizad建立的入流模型联合使用，而后者尚未公开。

图18 ONERA 涡环状态边界[18]Fig.18 ONERA vortex ring state boundary[18]

3.3 经验化涡环状态边界

NASA AMES 中心的Johnson[19]将直升机浮沉方向速度不稳定性区间作为进入和退出涡环状态的界定准则（图19），认为CEV 的D6075 飞行试验结果[18]和美国海军联合波音公司开展的V–22 飞行试验结果[3]反映了这一现象，根据上述飞行试验结果划定了下降飞行稳定性边界。

图19 NASA 涡环状态边界[19]Fig.19 NASA vortex ring state boundary[19]

而后，Johnson 进一步将此边界作为d(VY+v1)/dVY=0 的分界点，建立了涡环状态下适用的旋翼入流模型，图9 中的N 点与X 点即为由该模型表征的进入和退出涡环状态的边界，其函数为：

式中：VYN、VYX分别为进入与退出涡环状态的下降飞行速度。

在2.1 节中，依据下降速度增大时旋翼拉力阻尼与旋翼性能恢复的先后关系，讨论了直升机恢复飞行平衡的时机。因此，虽然Johnson 的本意是由图9中的X 点判定退出涡环状态，但就CEV 对飞行试验数据的处理方式而言，其结果实质是在旋翼总距维持进入涡环状态前的水平时，旋翼拉力恢复至悬停状态下的拉力大小的情况。

3.4 涡环状态边界模型的差异与适用性分析

1）边界曲线形态不同。随着前飞速度增大，高-辛边界中进入涡环状态的临界下降速度显著增大，NASA 边界与之类似但斜率大幅减小，而ONERA边界呈现出略微降低的趋势，这些差异导致了对前飞速度增大时是否能放宽下降飞行速度限制看法的偏差。

高-辛边界与ONERA 边界同为以桨尖涡运动速度刻画对涡环状态逼近程度的半经验模型，二者对桨尖涡速度表征方式的不同导致了临界下降速度随前飞速度变化规律的差异。NASA 边界是基于数理统计模型对2 组飞行试验结果规律进行抽象得到的，其上边界形态依据V–22 与D6075 飞行试验结果规律划定，但忽略了VX/vh<0.6 时D6075 直升机进入涡环状态临界速度的规律。

2）垂直下降状态的临界速度不同。高-辛边界基于悬臂机试验获得的固定总距下旋翼功率变化趋势转折点，将垂直下降状态临界速度认定为-0.28vh，随后由构建的判别式给出退出涡环状态的临界速度（约-1.8vh）。ONERA 边界与NASA 边界的垂直下降临界速度都参考了CEV 的 D6075 的试飞结果，前者为-0.63 vh、-1.47 vh，后者为-0.45 vh、-1.5vh。二者差异产生于对垂直下降附近离散飞行结果的逼近过程中，由于近似模型在VX/vh=0 附近斜率不同，导致边界曲线与纵坐标的交点不同。

3）高-辛边界相对于ONERA 边界和NASA 边界较为保守，陆洋等[34]使用R22 直升机对高-辛边界进行试飞验证后指出：高-辛边界更适宜作为涡环状态之前的告警边界。ONERA 边界和NASA 边界均参考飞行试验数据结果建立，描述了直升机浮沉运动失稳与飞行平衡重新恢复的现象，但受试验数据离散度和近似表达式的影响，其构建中仍引入了一定的主观因素。

3.5 改进方向

从涡环状态边界模型的差异对比中可知，模型的真实性取决于近似表达式和试验数据的质量。因此，一方面，需要能更真实地反映物理机制的近似表达式；另一方面，需要更稳定的试验数据，避免数据离散性对模型置信度的影响。此外，多位研究者认为，旋翼轴流状态试验须在大型风洞中使用小尺寸旋翼开展[19,47]。

4 风洞试验和涡环状态边界构建

4.1 下降状态旋翼气动特性风洞试验

4.1.1 试验方法

旋翼拉力及其阻尼特性是评估涡环状态边界的重要指标，通过设计总距恒定、下滑角不同的多种工况，评估拉力性能、拉力阻尼、桨盘入流（需用功率）随来流条件的变化。根据旋翼性能试验结果计算桨盘入流的方法参见文献[18-19]。

4.1.2 试验模型

旋翼气动外形可能对涡环状态特性造成不同影响，为了扩大试验结果的适用范围，选取4 副不同桨尖形状、扭转角、翼型配置的旋翼模型作为测试对象，其参数如表2所示。

表2 旋翼模型参数Table 2 Parameters of rotor models

4.1.3 试验设备

试验在大型低速风洞开口试验段开展，风洞喷口尺寸为8 m×6 m，最高阻塞比约0.036，低于表1中除全尺寸风洞外的大部分风洞试验的阻塞比。旋翼拉力由五分量天平测量，旋翼扭矩由LORNZE DR2400 扭矩传感器测量，转速和方位角由安装在电机轴的编码器测量，试验场景如图20所示。

图20 风洞试验照片Fig.20 Wind tunnel test photo

4.1.4 试验状态

如图21所示，试验风速范围：悬停，来流速度V∞=4.5～20 m/s；下滑角α=90°～40°。测量参数包括旋翼拉力和扭矩（2 号旋翼仅测量了拉力，未测量扭矩）。

图21 试验风速与下滑角示意图Fig.21 Schematic diagram of glide angle between test wind speed and rotor

4.2 试验结果及分析

图22 为4 副旋翼垂直下降状态（α=90°）的拉力系数Ct、桨盘入流（VY+v1）、功率系数Cp与悬停状态下功率系数（用下标0 表示）的比值，试验结果随风速的变化规律与前人结果（图7[39]、图9[19]）一致。图22 中旋翼拉力和桨盘入流随风速变化的转折点基本一致，反映了二者背后相同的物理机制。图22（c）中功率比值整体变化趋势与图22（a）中拉力变化趋势基本一致，反映了桨叶剖面迎角变化对翼型阻力和升力的影响。但功率比值在VY/vh=-0.4～-0.8 时出现了与图7（b）中类似的不光滑特征，且变化幅度显著弱于拉力和桨盘入流。

图22 旋翼在垂直下降状态的气动特性Fig.22 Aerodynamic characteristics of each rotor in vertical descent

对比图22 中各副旋翼的拉力和需用功率特性可以发现：3 号旋翼在涡环状态下的性能损失最小；4 号旋翼的拉力损失最大，VY=-1.2 vh时的拉力仅为悬停状态的70%左右，其需用功率却达到悬停状态的160%，而大多数直升机的功率裕度很难满足在该状态下拉起直升机的要求。

图23 为1 号旋翼在不同下滑角条件下的拉力与桨盘入流情况。随着下滑角减小，即前进比增大，旋翼进入涡环状态后拉力下降幅度和桨盘入流增大幅度降低，同时拉力恢复至悬停值对应的横坐标略微靠左，这说明功率沉陷严重程度和退出涡环状态对应的下降速度随前飞速度增大而减小。观察曲线的左侧区域可见：随着下滑角减小，拉力负阻尼效应出现时所对应的横坐标略微向左移动，这意味着进入涡环状态所对应的下降速度随前飞速度增大而略微减小。

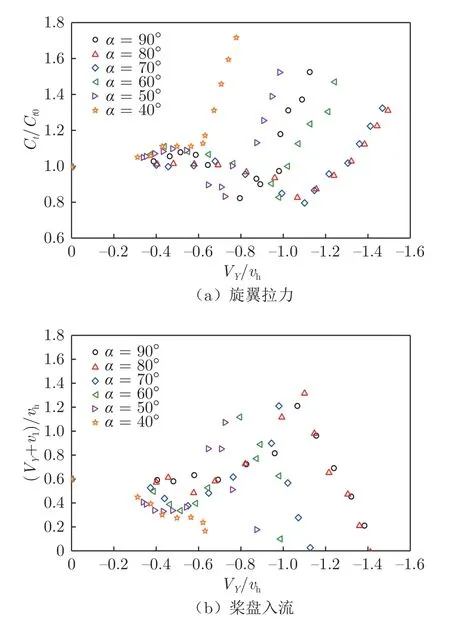
图23 1 号旋翼在不同下滑角下的气动特性Fig.23 Aerodynamic characteristics of No.1 rotor at different glide angles

图24 为2 号旋翼在40°下滑角下的拉力特性。由图可知：下滑角为40°时，各下降速度下的旋翼拉力均高于悬停状态，桨盘入流均低于悬停状态，表明这个阶段不会发生功率沉陷现象，CEV 以图4 的方式进行飞行试验时未经历下降速度突增也证明了这一点；VY/vh=-0.4～-0.6 时拉力趋平，反映了拉力负阻尼和中立稳定现象依然存在。

图24 2 号旋翼在40°下滑角下的拉力特性Fig.24 Thrust characteristics of rotor 2 at 40 ° glide angle

针对图23（a）中下滑角为90°～50°时，在首个下降速度试验点至拉力极小值对应的区间内，对拉力数据进行多项式拟合并求导，以导数为0 时对应的下降速度作为进入涡环状态的临界速度；在拉力达到极小值之后的区间内，进行多项式拟合并求出Ct/Ct0=1 所对应的下降速度，将其作为退出涡环状态的临界速度。针对40°下滑角状态，对拉力趋平前后区间的数据进行多项式拟合并求导，以导数值突变作为涡环状态临界速度的判断依据。对各副旋翼重复以上操作，得到本次试验提取的涡环状态边界临界速度，如图25所示，各副旋翼的偏差值约为0.1。

图25 从风洞试验数据提取的涡环状态边界Fig.25 Vortex ring state boundary extracted from wind tunnel test data

4.3 涡环状态边界半经验公式构建

在试验数据中，可以观察到与Wolkovitch 边界、Newman 等、ONERA 边界相似的临界下降速度随前飞速度增大而减小的特征，这些边界均使用旋翼诱导速度和自由来流速度叠加描述桨尖涡的运动速度。Newman 等和ONERA 边界使用桨尖涡运动速度绝对值低于阈值（即桨尖涡向上或向下运动速度的极值）的方式表征进入或退出涡环状态的边界，避免了Wolkovitch 等和Peters 边界采用2 种公式分别表征上、下边界带来的不便。此外，通过改变临界值可实现边界范围成比例放大或缩小，可在机载设备中实时评估危险程度的高低。因此，本文拟借鉴Newman 等和ONERA 边界的思想构造涡环状态边界半经验表达式。

桨尖涡聚集形成涡环并逼近旋翼是涡环状态的核心流动机制，但其涉及的环节十分复杂，难以采用事先确定的参数描述。涉及的环节有：1）桨尖涡垂向速度不可能严格等于（VY+v1）/2；2）桨尖涡聚集形成的涡环不可能总位于桨盘，使用桨盘处的诱导速度来计算其运动速度与实际流场不符；3）进入与退出涡环状态对应的桨尖涡运动正、负速度临界值不可能完全对称；4）前飞速度不仅参与桨尖涡运动的驱动，还控制边界的最大前进比，其加权可能存在非线性规律；5）涡环状态边界对应的临界值可能随前飞速度变化而变化。上述各环节所对应的表征参数无法直接由其内部机理确定，须将其作为灰箱系统处理，借助试验结果拟合寻找合适的值。

将涡环状态边界理论近似表达式设计成式（13）为下式：

式中：k1（VX/vh）n1表征前飞速度对桨尖涡的驱动力，k1与n1起着控制不等式左边项在大前进比下饱和的作用；k2v1/vh表征诱导速度对桨尖涡的驱动力，k2用于调节诱导速度与自由来流速度轴向分量对桨尖涡驱动作用的强弱；VY/vh表征下降速度对桨尖涡的驱动力；k3（VX/vh）n2表征在不同前进比下对用动量定理计算的桨盘入流结果的修正；(k4VX/vh+ε0)表征不同前飞速度下桨尖涡运动速度的临界值。

采用最小二乘算法，以图25 中的数据为样本，对式（13）中的未知参数进行求解，得到涡环状态边界的半经验公式：

图26 为基于式（14）得到的涡环状态边界与本文风洞试验及CEV 飞行试验结果对比。式（14）得到的进入涡环状态的临界下降速度随前飞速度略有减小，与CEV 飞行试验结果趋势一致。这主要是由于旋翼诱导速度随着前飞速度增大而降低，加剧了下降飞行中桨尖涡趋向上游的运动。这表明在实践中，即使有前飞速度，仍不可放宽对下降速度的限制。

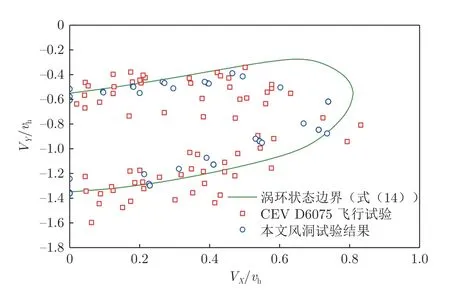
图26 式（14）计算的涡环状态边界与风洞试验和CEV 飞行试验结果对比Fig.26 Comparison of vortex ring state boundary calculated by equation 14 with wind tunnel test results and CEV flight test results

需要指出的是，本文和表1 中的旋翼涡环状态性能试验均在桨盘倾角为0°的情况下开展。Taghizad将CEV 试验中的旋翼姿态角还原后，认为其飞行试验结果的桨盘倾角小至可忽略[18]，因而目前所发展的涡环状态边界均未考虑桨盘倾角的影响。直升机低速稳定下降飞行时的桨盘倾角普遍较小，但在拉平减速等大俯仰角姿态机动时，必须考虑桨盘倾角的修正，如1.1 节分析的Mi-8T 直升机事故，就是在拉平减速中沿旋翼轴向进入桨盘的气流剧增，导致直升机进入涡环状态[8]。此外，在实际应用中还需考虑环境风的影响，如2020年法国陆军AS332 直升机就在着陆时因遭遇顺风而进入涡环状态导致失事[7]。