Top-k高模糊效用项集挖掘算法

王 斌，周 伟，李晓华，胡克勇

(青岛理工大学 信息与控制工程学院，山东 青岛 266520)

0 引 言

在数据挖掘中，高效用项集挖掘算法是一项重要的研究课题[1-6]。然而，高效用项集挖掘算法的输出结果中，只包含项集的组成项及效用信息。决策者很难从中获取到其它信息，例如高效用项集中每个项的数量区间，导致无法做出精确的决策。

为解决这一问题，模糊集理论引入到了高效用项集挖掘中，产生了高模糊效用项集挖掘算法。HFUI-GA[7]将进化计算方法引入了高模糊效用项集挖掘中。EFUPM[8]算法提出了紧密的模糊效用上界模型，有效减少了搜索空间。

上述高模糊效用项集挖掘算法，均需要事先确定最小模糊效用阈值，再去挖掘模糊效用值不小于阈值的高模糊效用项集(high fuzzy utility itemset，HFUI)。然而，阈值的设定并非易事。如果阈值设置太低，会输出大量的HFUI；如果阈值设置太高，会产生极少的HFUI。用户都不能从结果中发现真正有用的项集。通常，研究人员会多次更换阈值，重复运行算法，直至找到最合适的阈值。显然，这种方法很不高效。为解决阈值选择的难题，受Top-k高效用项集挖掘算法的启发[9-15]，本文将设定阈值的问题转化成设定所需高模糊效用项集数量k的问题，提出了Top-k高模糊效用项集挖掘TKHFU。该算法设计了一种模糊项集效用列表结构，避免了项集间复杂的连接过程；提出了两种有效的剪枝策略Afu-Prune和FI-Prune，并将两种剪枝策略与列表结构进行结合，减少了无意义项集列表的构建，提升了算法的性能。

1 相关定义

给定一个含有m个不同项的有限项集合I={i1，i2，i3，…，im}，称此集合为m-项集。设含有n条事务的定量事务数据库D={T1，T2，T3，…，Tn}，任意事务Ty(1≤y≤n) 是I的一个子集。任意项iz∈Ty，有一个内部效用q(iz，Ty) (数量)，外部效用p(iz) (单元利润)。一个定量事务数据库如表1所示，其各项单元利润见表2。本研究中，对表1中的各项使用相同的隶属函数，均有3个模糊域，分别为低(L)、中(M)、高(H)。

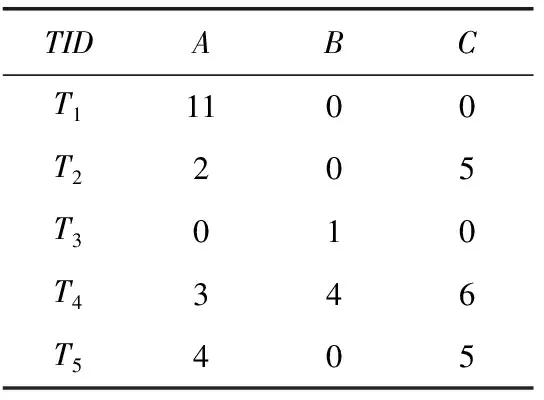
表1 定量事务数据库

表2 单元利润

定义1[8］第y条事务Ty中第z项iz的数量vyz的模糊集用fyz表示，可由给定的隶属函数描述为

(1)

其中，h是项iz的隶属函数(模糊域或语义术语)的数量，Rzl是项iz的第l模糊域，fyzl是第z项的数量vyz在第l模糊域Rzl的模糊隶属度，且fyzl∈[0，1]。

例如，表1中T4的项B的数量(=4)可以由图1中隶属函数转换成f4，B=(0.4/B.L，0.6/B.M，0/B.H)。

图1 隶属函数

定义2 事务Ty中项iz的效用，是其数量和单元利润的乘积，用u(iz，Ty) 表示，定义为

u(iz，Ty)=q(iz，Ty)×p(iz)

(2)

定义3[8］事务Ty中项iz的第l模糊域的模糊效用，用fuyzl表示，定义为

fuyzl=fyzl×u(iz，Ty)

(3)

例如，由表1、表2和图1可知，表1的T2中项A的数量为2，单元利润为1，A的第一个模糊域A.L的隶属度为0.8，则fu2，A.L=0.8×2×1=1.6。按此计算方式，我们计算出了表2中所有项的各模糊域的模糊效用，见表3。

表3 定量事务数据库中各项模糊域的模糊效用

定义4[8］事务Ty中模糊项集X的模糊效用fuyX是X中所有模糊项的模糊效用之和，定义为

(4)

在模糊项集X中，模糊项fizl是指，带有第l模糊域的项iz。值得注意的是，模糊项集中的模糊项，只能来自不同的离散项。

例如，设X={A.L，C.M}，模糊项A.L和C.M分别来自项A和C。由表3可知，事务T2中X的两个模糊项的模糊效用分别为1.6和20，则fu2，X=1.6+20=21.6。

定义5 模糊项集X的实际模糊效用，用afuX表示，是事务数据库D中所有包含IX的事务中的X的模糊效用总和，定义为

(5)

其中，IX是模糊项集X的原始离散项集。例如，设X={A.L，C.M}，则其IX={A，M}。由表3可知，模糊项集X的实际模糊效用为：afuX=fu2，X+fu4，X+fu5，X=(1.6+20)+(1.8+30)+(1.6+20)=75。

定义6 由用户预设一个最小模糊效用阈值，用min_futil表示。模糊项集X是高模糊效用项集，当且仅当afuX≥min_futil。用HFUI表示高模糊效用项集。

现有高模糊效用项集挖掘算法，需先设置最小模糊效用阈值min_futil，再去挖掘实际模糊效用值不小于min_futil的HFUI。然而，阈值的设定并不容易。如果阈值设置得太低，将会产生大量的HFUI，用户很难去发现真正有趣的项集，算法的性能也会严重衰减，同时会消耗大量的内存。而如果阈值设置得太高，算法将产生很少的HFUI，用户同样也无法发现有趣的项集。通常，研究人员采用试错的方法。即，不断更换阈值，重复算法，直至找到最合适的阈值。显然，这种方法是不高效的。

鉴于上述问题，本文借鉴了Top-k高效用项集挖掘算法的思想[9-15]，将设定min_futil的问题转化成设定所需高模糊效用项集数量k的问题，提出了Top-k高模糊效用项集挖掘的概念，如下定义7。

定义7 给定一个定量事务数据库D及用户指定的正整数k，Top-k高模糊效用项集挖掘，记作TKHFU，旨在发现前k个具有最大模糊效用的模糊项集。

定义8[8］事务Ty中，项iz的最大模糊效用定义为

mfuyz=max{fuyz1，fuyz2，…，fuyzl}

(6)

其中，fuyzk(1≤k≤l) 是事务Ty中项iz的第k模糊域的模糊效用。例如，由表3可知，事务T4中，项B的最大模糊效用mfu4，B=max{fu4，B.L，fu4，B.M，fu4，B.H}=19.2。

定义9[8］事务Ty中模糊项集X的项集最大事务模糊效用，用imtfuyX表示，定义为

(7)

例如，设X={A.L，C.M}，由表3可知，X在T4中的项集最大事务模糊效用为：imtfu4，X=fu4，X+mfu4，B=(1.8+30)+19.2=51。

定义10[8］模糊项集X的项集模糊效用上界，用ifuubX表示，是数据库D中所有包含IX的事务中X的项集最大事务模糊效用的总和，定义为

(8)

例如，设X={A.L，C.L}，其IX={A，C}。由表3可知，X的项集模糊效用上界为：ifuubX=imtfu2，X+imtfu4，X+imtfu5，X=34.2。

定义11 给定一个有限项的集合I={i1，i2，i3，…，im}，设是作用于I中的排序符号。令I中的项按字典顺序升序排序，即i1i2i3…im。设模糊项集X的离散项集IX={x1，x2，x3…，xL}⊆Ty，其中x1x2…xL，Ty⊆I。将Ty排序后，若存在ij∈Ty且满足xkij，k∈(1，L)，则将Ty中出现在IX之后的项集称作IX的剩余项集，记作Ty/IX。

例如，表1中项的顺序为ABC，T4={A，B，C}，设IX={B}，则IX剩余项集Ty/IX={C}。

定义12 事务Ty中模糊项集X的最大剩余模糊效用，记作mrfuyX，定义为

(9)

例如，设X={A.L，B.L}，其IX={A，B}。由表3可知，在事务T4中T4/IX={C}，则X在T4中的最大剩余模糊效用为：mrfu4，X=mfu4，C=30。

定义13 事务Ty中模糊项集X的最大事务模糊效用等于其模糊效用与最大剩余模糊效用之和，记作mtfuyX，定义为

mtfuyX=fuyX+mrfuyX

(10)

例如，设X={B.L}，其IX={B}。由表3可知，在事务T4中T4/IX={C}，则X的最大事务剩余模糊效用为：mtfu4，X=fu4，X+mrfu4，X=fu4，X+mfu4，C=12.8+30=42.8。

性质1 给定模糊项集X及其扩展项集X′，其中X⊂X′，IX⊆Ty，则有

imtfuyX≥mtfuyX≥fuyX′

(11)

证明：

(1)imtfuyX≥mtfuyX：

(2)若IX′⊄Ty：

∵fuyX′=0 ∴mtfuyX≥fuyX′

(3)若IX′⊆Ty：

mtfuyX=fuyX+mrfuyX

≥fuyX+fuy(X′-X)+mrfuyX′

=fuyX′+mrfuyX′≥fuyX′

∵(1)和(2)∴imtfuyX≥mtfuyX≥fuyX′。

定义14 定量事务数据库D中，模糊项集X的模糊项集效用上界，记作fiuubX，定义为

(12)

例如，设X={B.L}。由表3可知，X的模糊项集效用上界fiuubX=mtfu3，X+mtfu4，X=(8+0)+(12.8+30)=50.8。

性质2 给定模糊项集X及其扩展项集X′，其中X⊂X′，IX⊆Ty，则有

ifuubX≥fiuubX≥afuX′

(13)

证明：∵性质1∴imtfuyX≥mtfuyX≥fuyX′

→ifuubX≥fiuubX≥afuX′，得证。

由性质2可知，本文提出的fiuub是比文献[8]中的ifuub更紧密的模糊效用上界。

定义15 Top-k项集列表结构，记作Topk-List，负责保存挖掘过程中发现的k个潜在Top-k高模糊效用项集，随挖掘过程不断更新。边缘模糊效用阈值，记作min_futilBorder，用于记录Topk-List中k个项集中的最小实际模糊效用值(记作Topk-List.minafu)，随Topk-List.min的更新而更新。

其中，潜在Top-k高模糊效用项集，指的是挖掘过程中实际模糊效用值afu不小于当前的边缘模糊效用阈值min_futilBorder的模糊项集。

2 算法设计

2.1 模糊项集效用列表

如图2所示，我们设计了一种用于保存模糊项集及其效用信息的数据结构，即模糊项集效用列表，用fiul表示。fiul由模糊项集(X)、事务标识符(tid)、事务中模糊项集的模糊效用(fu)、事务中模糊项集的最大剩余模糊效用(mrfu)组成。列表中fu之和用sumFu表示，mrfu之和用sumMrfu表示。图2中的模糊项集来自表3，列表中数据可由表3计算得到。由列表计算可知，1-项集的实际模糊效用afu和模糊项集效用上界fiuub。例如，{A.L}的模糊项集效用上界fiuub{A.L}= (1.6+20)+(1.8 +49.2)+(1.6+20)=94.2，afu{A.L}=1.6+1.8+1.6=5。

图2 模糊1-项集的效用列表

借助列表结构，不需要重复扫描数据库，便可将两个不同(k-1)-项集的fiul进行连接，形成一个新的k-项集(k≥2)的fiul。两个项集进行连接操作时，具有相同的tid的元组会结合在一起。为了加速连接过程，规定列表的每一列按照tid升序排序，可采用二分查找的方式去定位元组。假设两个不同列表的大小分别为m和n，由于列表中的tid按升序排序，则在最坏情况下，时间复杂度为O(m+n)。图3是2-项集的列表结构。各元组fu的值等于项集中各模糊项在同一事务中的模糊效用之和。由定义13及定义14分析可知，两不同(k-1)-项集连接时，应取事务中顺序靠后的模糊项集的mrfu的值作为k-项集的mrfu的值。例如，mrfu4，{A.L，B.L}=mrfu4，{B.L}=30。

图3 模糊2-项集的效用列表

2.2 剪枝策略

根据上一节提出的列表结构，项集间连接方式的搜索空间可视作一棵集合枚举树，如图4所示。由图4可知，由于树中存在大量的节点，搜索过程会变得非常耗时。如果存在n个模糊项，则意味着需要检索2n个模糊项集。因此，为减少搜索空间，本文提出了两种剪枝策略。相关描述如下。

图4 用例的集合枚举树

性质3 Afu-prune：给定模糊项集X及其模糊项集效用列表fiulX。在挖掘过程中，若fiulX中所有的fu之和不小于当前的边缘模糊效用阈值min_futilBorder，则X是一个潜在Top-k高模糊效用项集，可添加到Topk-list中。

证明：给定模糊项集X及相应的模糊项集效用列表fiulX，设X.tids是fiulX中tid的集合，则有

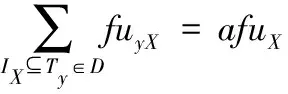
由定义15可知，X是潜在的Top-k高模糊效用项集，可将X加到Topk-list中。

性质4 FI-Prune：给定模糊项集X及其模糊项集效用列表fiulX。若fiulX中所有的fu及mrfu的总和不小于当前的边缘模糊效用阈值min_futilBorder，则存在X的扩展项集X′可能是潜在Top-k高模糊效用项集。否则，就无需去构建一个新的项集模糊效用列表。

证明：设模糊项集X的扩展为X′。由性质2可知，X′实际模糊效用afuX′≤fiuubX。由定义13和14可知，fiuubX=sumFuX+sumMrfuX。

因此，若sumFuX+sumMrfuX

例如，设k=2，由表3创建1-项集模糊项集效用列表后，计算实际模糊效用，可得最大的两个项集为{C.M}和{B.L}。根据性质3，Top2-list更新后，其中保存的项集为：{{B.L}，{C.M}}，min_futilBorder=afu{B.L}=20.8。考虑1-项集{A.M}及其扩展项集{A.M，B.M}，由于sumFu{A.M}+sumMrfu{A.M}=93.2>min_futilBorder，根据性质4，{A.M，B.M}可能是潜在Top-k高模糊效用项集，则构建其模糊项集效用列表。计算sumFu{A.M，B.M}=21.4，sumFu{A.M，B.M}>min_futilBorder。根据性质3，2-项集{A.M，B.M}是潜在Top-k高模糊效用项集，可添加到Top2-List。更新Top2-List：{{A.M，B.M}，{C.M}}，更新min_futilBorder=afu{A.M，B.M}=21.4。

2.3 TKHFU算法

根据上述内容，本文已经介绍了TKHFU算法的相关定义、数据结构及剪枝策略。接下来，开始详细介绍本算法的挖掘过程。

算法1是TKHFU的主函数，其输入参数包括：定量事务数据库D，期望发现的高模糊效用项集的数量k，模糊隶属函数R。输出Top-k高模糊效用项集的集合TKHFUs。第(1)步～第(5)步，TKHFU检索数据库D中的每一条事务Ty，将Ty中每个项按给定的模糊隶属函数转化成模糊项，计算每个模糊项的模糊效用fu及最大剩余模糊效用mrfu。然后，按定义11对事务中各项排序，得到修改后的数据库(第(6)步)。之后，初始化共同前缀项集及其模糊项集效用列表，以便后续构建高层级的模糊项集(第(7)～第(8)步)。初始化Topk-List为NULL，边缘模糊效用阈值为0(第(9)步)。然后，构造所有一项集的效用列表，得到一项集所有列表的集合fiul1(第(10)～第(12)步)。第(13)步，调用算法2，递归挖掘Top-k项集。最后，输出Top-k高模糊效用项集的集合TKHFUs。

算法1：TKHFU

输入：定量事务数据库D，k，模糊隶属函数R。

输出：Top-k高模糊效用项集的集合TKHFUs。

(1)foreach transactionTyinDdo

(2) Convert the value of all every itemiz∈IinTyto fuzzy items byR;

(3) compute the fuzzy utility value of every fuzzy item(fu);

(4) calculate the maximal remaining fuzzy utility value of every fuzzy item inTy(mrfu);

(5)end

(6) sort all itemsiz∈IinTywith thei1i2i3…imorder then get revised transactions;

(7) initial common prefix itemsetP←NULL;

(8) initial fuzzy itemset utility list ofP,fiulP←NULL;

(9) initial Topk-List←NULL,min_futilBorder←0;

(10)foreachiz∈Ido

(11) getfiulof every fuzzy item ofiz(fiul1);

(12)end

(13) callMiner(P,fiulP,fiul1,Topk-List,min_futilBorder);

(14)returna complete set of TKHFUs;

算法2是一个递归函数，输入参数包括：共同前缀模糊项集P，P项集模糊效用列表fiulP，模糊项集效用列表的集合fiuls，Top-k模糊项集列表结构Topk-List，边缘模糊效用阈值min_futilBorder。对于任意fiulX∈fiuls，首先判断X是否为潜在候选Top-k高模糊效用项集。根据性质3，如果fiulX中所有的fu之和不小于当前的边缘模糊效用阈值min_futilBorder，则将X添加到Topk-List中。之后，移除Topk-List中实际模糊效用值最小的项集，将边缘模糊效用阈值更新到当前Topk-List中的最小实际模糊效用值(第(2)步～第(5)步)。然后，根据性质4，如果fiulX中所有的fu及mrfu的总和不小于当前的边缘模糊效用阈值min_futilBorder，那么存在X的扩展项集可能是潜在Top-k高模糊效用项集，则可用X去构建高层级的模糊项集(第(7)步～第(15)步)。第(8)步，使用exfiuls收集新的扩展模糊项集的列表，并将其初始化为NULL。第(9)步，由于所有的1-项集是排好序的，因此只需要考虑fiulX之后的fiulY即可。调用算法3去构建新的高层级的模糊项集的效用列表(第(10)步)。最后，程序设置新的输入参数，递归地执行算法，直到挖掘出全部的Top-k项集(第(16)步)。

算法2：Miner

输入：共同前缀模糊项集P，P项集模糊效用列表fiulP，模糊项集效用列表的集合fiuls，Top-k模糊项集列表结构Topk-List，边缘模糊效阈值min_futilBorder。

(1)foreachfiulXinfiulsdo

(2)ifsumFuthen

(3) Topk-List←X;

(4) Remove fuzzy itemset with minimal actual fuzzy utility from Topk-List;

(5)min_futilBorder←Topk-List.minafu;

(6)end

(7)ifsumFuX+sumMrfuX≥min_futilBorderthen

(8) initialexfiulswhich is a new set of extended fuzzy itemset uitility listsfiulsasNULL;

(9)foreachfiulYafterfiulXinfiulsdo

(10) newfiultmp←Construct(fiulP,fiulX,fiulY);

(11)ifsumFutmp> 0then

(12) addfiultmpintoexfiuls;

(13)end

(14)end

(15)P←P∪X;

(16) callMiner(P,fiulX,exfiuls,Topk-List,min_futilBorder);

(17)end

(18)end

算法3以3个模糊项集效用列表作为输入参数，负责使用两个不同项集的列表去构建新的高层级项集的列表。对于1-项集的列表，它们的共同前缀设定为NULL。第(1)步，初始化新的扩展模糊项集Pxy的列表。然后，遍历Px的列表中每个元素Pxe(第(2)步)。如果Py的列表fiulPy中存在元素Pye与Pxe有相同的tid，那么模糊项集Px和Py可用于形成一个新的模糊项集Pxy(第(5)步～第(6)步)。Pxye.fu的值应该减去Pe.fu的值，以避免重复计算(第(6)步)。此外，如果Px和Py是1-项集，那么程序会去构建一个Pxy列表的新元素Pxye，计算相应的fu及mrfu的值(第(8)步)。由于定量事务数据库已经过修改，Pxye的mrfu的值应为Pye.mrfu。第(10)步，将构建好的Pxye添加到fiulPxy中。最后，算法3返回一个新的列表fiulPxy。

算法3：Construct

输入：共同前缀模糊项集的效用列表fiulP，模糊项集Px的效用列表fiulPx，模糊项集Py的效用列表fiulPy。

输出：一个新的高层级的模糊项集的效用列表

(1) initialfiulPxy←NULL;

(2)foreach elementPxe∈fiulPxdo

(3)if∃Pye∈fiulPyandPxe.tid==Pye.tidthen

(4)iffiulP≠NULLthen

(5) adopt binary search method find elementPe∈fiulPwhichPe.tid==Pxe.tid;

(6)Pxye=(Pxe.tid,Pxye.fu-Pe.fu,Pye.mrfu);

(7)else

(8)Pxye=(Pxe.tid,Pxye.fu-Pe.fu,Pye.mrfu);

(9)end

(10) addPxyeintofiulPxy;

(11)end

(12)end

(13)returna fuzzy itemset utility list of new fuzzy itemsetPxy

2.4 时间复杂度分析

本算法的时间复杂度主要由算法1的步骤(1)和步骤(13)决定。步骤(1)是遍历数据库中的事务及对每条事务中的项进行处理，执行次数主要由事务数m和事务中的项数n决定，执行次数为mn。算法1的步骤(13)为算法2，是一个递归函数，其执行次数等于递归次数×每次递归执行次数。由算法2的步骤(7)可知，递归次数由if语句成立的次数q决定，q不大于步骤(1)中列表的数量p。算法2每次递归的执行次数由(1)、(9)和(10)决定。(1)是一个外循环，执行次数由列表的数量p决定。(9)是一个内循环，执行次数由排在模糊项集X后的模糊项集Y的数量x1决定。(10)是算法3，执行次数由算法3中的步骤(2)决定。算法3中，设fiulPx和fiulPy中元素数量分别为x2和x3，查找相同tid的元素，最坏情况下，执行次数为x2+x3。因此，算法1步骤(13)的执行次数为qp(x2+x3)。综上，本算法总体时间复杂度为O(mn+qpx1(x1+x3))。

3 实验分析

实验平台：Windows 10操作系统，16 G内存，Intel(R) Core(TM)i5-9300H CPU @2.40 GHz。本实验中所有算法均采用java实现。实验中用到的数据集，包括真实数据集和合成数据集，其特征见表4。数据集foodmart和Skin属于真实数据集，来源于SPMF[16]；c4d250k是由SPMF上的spmf.jar发行版工具合成的一组数据集；项的数量在1～12之间随机产生，项的单元利润在1～8之间随机产生。本文从运行时间、内存占用及可伸缩性3个方面对算法性能进行了评估。

表4 数据集特征

为评估TKHFU的性能，本节将其与HFUI-GA[7]及EFUPM[8]进行了比较。由于HFUI-GA和EFUPM是高模糊效用项集挖掘算法，无法直接与TKHFU比较。为比较这3种算法，可采取先确定k值来运行TKHFU，再取算法挖掘结果中第k项的afu的值作为HFUI-GA和EFUPM的min_futil的方法。本文从运行时间、内存占用及可伸缩性3个方面评估了3种算法的性能。

3.1 时间和内存分析

图5显示了3种算法在真实数据集foodmart和Skin上运行时间的比较。在较小的数据集foodmart上，当k值等于200时，TKHFU算法仅需2 s，而HFUI-GA和EFUPM运行时间分别需要11 s和5 s。在较大的数据集Skin上，TKHFU算法表现同样出色，TKHFU算法不仅所需时间最少，而且随着k值的增长，时间变化也较其它两者更为平稳。当k值从1上升到100时，TKHFU运行时间仅从3 s上升到6 s，而HFUI-GA算法已经从20 s上升到51 s，EFUPM也从7 s上升到了18 s。主要原因是，算法只扫描了一次数据库，构建一项集的模糊项集效用列表之后，直接根据列表中tid来产生高层级的项集，大大减少了项集连接操作的耗时；其次，使用了两种有效的剪枝策略，减少了非潜在Top-k高模糊效用项集的产生，避免了创建无意义项集的列表所需的时间。

图5 TKHFU和EFUPM及HUFI-GA的运行时间

图6显示了3种算法在真实数据集foodmart和Skin上内存占用的比较。无论是在小数据集foodmart还是在较大数据集Skin上，TKHFU的内存占用情况均明显优于HUFI-GA算法，略好于EFUPM算法。原因主要是，TKHFU相较于HFUI-GA，使用了新的紧凑的数据结构，并将其与两种剪枝策略结合，避免占用大量内存去创建无意义的项集；TKHFU相较于EFUPM，改进了模糊效用上界，使用了一种更紧密的模糊效用上界，从而减少了内存消耗。

图6 TKHFU和EFUPM及HFUI-GA的内存消耗

总体来说，基于真实数据集的实验验证了TKHFU算法的可行性和有效性，表明了TKHFU算法的运行时间和内存占用都随k值增大而增大，但TKHFU在运行时间和内存占用方面均优于其它两种算法。

3.2 可伸缩性分析

图7显示了3种算法在不同条件下的可伸缩性。实验中，k值设定为50。图7(a)显示，在数据库大小固定为50 K，数据集c4d250k不同项的数量从1 K到5 K变化时，3种算法的运行时间。图7(b)显示，在不同项的数量固定为1 K，数据集c4d250k的大小从50 K到250 K变化时，3种算法的运行时间。分析可知，在不同设定条件下，TKHFU具有更好的伸缩性。

图7 不同条件下算法的可伸缩性

4 结束语

本文提出了TKHFU算法，解决了高模糊效用项集挖掘中存在的阈值选择的难题。设计了项集模糊效用列表结构，减少了项集间连接的时间。提出了一种更紧密的模糊效用上界及两种剪枝策略，将剪枝策略运用到了列表中，提升了算法的效率。基于两种真实数据集及一组合成数据集的实验结果表明，TKHFU在运行时间、内存占用及可伸缩性上均优于HUFI-GA及EFUPM。

未来，我们会进一步将提出的算法应用到实际中，例如数据流等。此外，采用基于树的结构及分布式架构，将算法运行在百万量级的超大数据集上，也是我们需要考虑的重点。