三自由度压电偏摆台耦合迟滞模型建模与逆补偿

司马津甫， 赖磊捷*， 李朋志， 方 宇*， 朱利民

（1. 上海工程技术大学 机械与汽车工程学院，上海 201620；2. 格鲁斯特大学 计算与工程学院，英国 切尔滕纳姆 GL50 2RH；3. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；4. 上海交通大学 机械与动力工程学院 机械系统与振动国家重点实验室，上海 200240）

1 引言

三自由度（Three Degrees of Freedom， 3-DOFs）压电驱动Z向/偏摆纳米位移台能够实现纳米精度的精密调平和指向等功能，在激光通信和精密跟踪瞄准、纳米光刻、微纳米操作机器人等领域都有着重要应用［1-2］。在其应用过程中，虽然压电陶瓷驱动器（Piezoelectric actuator， PZT）具有超高分辨率、承载力大、频响快、无噪声等优点［3］，但同时也存在迟滞和蠕变等非线性特性，这些非线性特性会严重影响纳米定位平台的定位精度，严重时会导致系统不稳定［4-5］。另外，并联式的多自由度定位平台由多个压电陶瓷同时驱动，每一个压电驱动器的运动都会在其他驱动器产生耦合迟滞输出，这同样会影响平台的定位精度。因此，建立考虑耦合迟滞效应的多自由度耦合迟滞模型及其补偿方法是提升三自由度压电偏摆台定位和跟踪精度的关键。目前，迟滞特性的建模方法已经有很多种，如Duhem 模型，Bouc-Wen 模型［6］，Preisach 模型［7］，Prandtl-Ishlinskii（PI）模型等［8-9］。其中PI 模型具有算法和逆模型求解简单、易于实时控制器实现等优点［10］，被广泛应用于迟滞特性的建模中。另外，为了描述率相关的动态迟滞特性，加拿大肯高迪亚大学的Janaideh 等人通过在密度函数以及算子阈值中引入输入信号的变化率，建立了可以表示迟滞率相关特性的PI 模型［11-12］。

为了解决耦合迟滞问题，目前主要方法是通过设计解耦柔顺机构以及通过平台控制进行补偿。但是，即便机械结构完全对称无耦合，由于安装误差等问题依旧会引起轴间的交叉耦合。因此，通过对平台的控制实现耦合补偿是当下的研究热点。耦合控制方法大致分为基于模型和无需模型两类。基于模型的耦合控制通常需要准确建立耦合模型并采用逆模型前馈来补偿耦合造成的误差，如澳大利亚新南威尔士大学的Petersen 等建立的多输入多输出模型［13］等。耦合模型一般较为复杂，难以通过有限阶数模型进行准确描述。在无需模型的耦合补偿控制中，各轴间耦合被认为是某一轴输出端的干扰，并以反馈控制的方式实现耦合的补偿，如澳大利亚莫纳什大学的Bhagat等建立的两轴鲁棒运动控制策略［14］等。

由以上分析可见，当前迟滞模型大多只能描述单轴迟滞特性，针对多轴耦合迟滞问题的研究还比较少见，这进一步增加了耦合迟滞补偿的难度和复杂程度。对此，本文以三自由度压电驱动纳米偏摆台为对象，设计了一种新型的耦合迟滞模型可以同时表征多个压电驱动器间的耦合效应以及自身的迟滞效应。该迟滞耦合模型由两部分组成，一部分是用三个PI 模型来表征压电驱动器自身非对称的迟滞效应，另一部分是使用九个增益来表征三轴间的耦合效应。通过求取该耦合迟滞模型的逆模型并进行开环前馈补偿验证了模型的有效性，并利用结合逆模型前馈和反馈的复合控制方法，来进一步消除系统耦合迟滞的影响，提升多轴运动的定位精度。

2 压电偏摆台及其模型

2.1 压电偏摆台实验系统

实验系统采用纳动纳米公司生产的型号为PT4V150-400S-S 的三自由度压电偏摆台，该平台通过三组彼此成120°分布的压电陶瓷驱动器进行驱动，其Z轴行程范围为0～200 μm，X轴和Y轴最大偏转角度分别为±2.2 mrad 和±2.5 mrad。压电驱动放大电源同样采用纳动纳米公司的PCM931S 模块化压电驱动/控制器。为实现平台的实时运动控制，利用两块PCI6221 数据采集卡和宿主机-目标机模式构建了基于Simulink xPC Target 的硬件在环半实物实时仿真系统。三自由度压电偏摆台实验系统以及各部件组成关系如图1 所示。

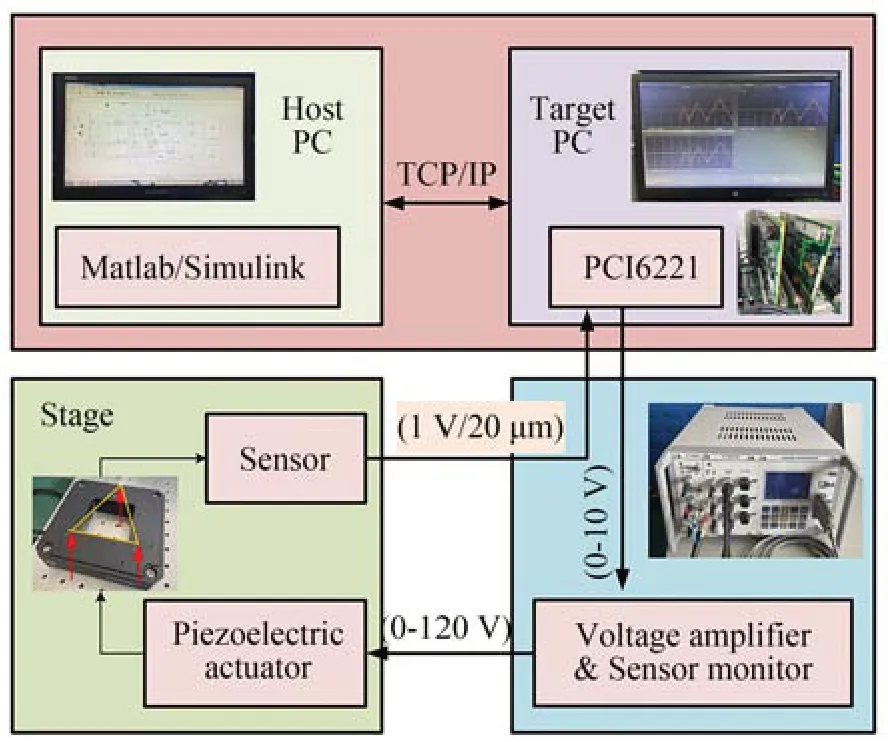
图1 三自由度压电偏摆台实验系统Fig.1 Experimental system of 3-DOFs tip-tilt-piston piezoelectric stage

2.2 压电偏摆台运动学模型

如图2 所示，D1，D2，D3分别为三组压电驱动单元的输出点位，它们构成一个等腰三角形，其中a=89 mm，b=77 mm。平台的三自由度分别为Z轴位移Δz以及分别绕X轴和Y轴的偏转角度θx，θy。为了将末端平台三自由度运动转化为三组压电驱动器的输出，将全局坐标系O-XYZ固定在图2 所示位置，其中D'4为D'2D'3的中点，O为D'1D'4的中点，θx，θy以如图2 所示情况为正角度。

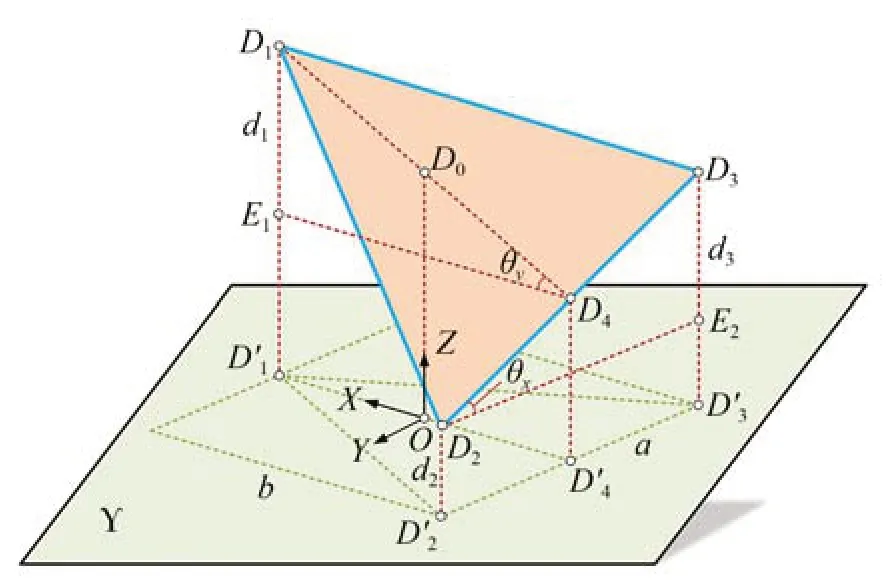
图2 三自由度运动与压电驱动器输出位移的关系Fig.2 Relationship between 3-DOFs motion and output displacements of PZTs

在施加电压前，压电驱动器D1，D2，D3的位置与平面Υ 上D'1，D'2，D'3的位置重合，施加电压后，三个压电驱动器分别产生位移d1=D1D'1，d2=D2D'2，d3=D3D'3，该三组位移可由压电驱动器内置的电阻式应变片传感器测量获得，由图2 所示的几何模型可得：

由此得到三自由度运动与三组压电驱动器输出位移之间运动学关系A如式（4）所示：

2.3 平台耦合迟滞特性

由平台运动学模型可知，平台末端位姿由三组压电驱动器输出位移计算获得，为了使末端位姿自由度间的耦合实现有效减少，需要对三个压电陶瓷驱动器间的耦合位移进行消除。因此，本文尝试对三个压电驱动器间的耦合位移进行补偿，此外三组驱动器间的解耦控制也更有利于单位的统一。

为了获得平台中压电陶瓷驱动器间的耦合迟滞特性，给压电驱动器1 施加如图3（a）所示的电压控制信号，采集的位移信号如图3 所示。ω（t）为输入电压信号，yr（t）为传感器采集的输出位移信号。

由图3（a）可见，平台中单个压电驱动器的输入与输出存在明显的迟滞非线性特性会严重影响闭环系统的定位精度与稳定性。此外，由图3（b）和图3（c）可以看出，当压电驱动器1 发生位移时，压电驱动器2 和3 在没有驱动信号输入的情况下也产生了一定的耦合位移，并呈现迟滞回线关系，由此可见，各组压电驱动器间还存在机械耦合迟滞效应，同样也会影响系统的定位精度与稳定性。并且在相同输入信号作用下，各驱动器的最大耦合位移也存在差别，这也增加了耦合迟滞建模的复杂程度。

3 耦合迟滞模型建模

迟滞非线性及其耦合效应都会严重影响纳米定位平台的定位精度，本节设计了一种可以同时准确描述多轴迟滞效应与耦合效应的耦合迟滞模型，该模型由两部分构成，第一部分由PI 模型来表征迟滞效应，第二部分由恒增益量来表征不同压电驱动器之间的耦合效应。

3.1 PI 迟滞模型

为了便于扩展并构建迟滞逆模型，本文选择PI 迟滞模型来表征平台的迟滞效应。PI 模型可以离散表达为：

其中：ω（t）为模型的输入，yd（t）为模型的输出，h（ω（t））为带有常量α和β的多项式函数，表达为：

其中：N为Play 算子的个数，rk为Play 算子的阈值，表达为：

pk为Play 算子的权重值，由实验数据辨识得到，［ω］（t）为Play 算子的输出，定义为：

其中：T为采样周期，dm(ω(t)，ω̇(t)) 和dn(ω(t)，ω̇(t))是输入函数ω（t）及其导数ω̇(t)的动态包络函数，定义为：

其中：γ和η为常数。由于输入函数ω（t）是周期很小的离散型函数，因此其导数ω̇(t)可以看作：

3.2 耦合迟滞模型

上文中的PI 模型可以很好地表征每一个压电驱动器的迟滞效应，但三自由度偏摆台中每一个压电驱动器发生位移时，都会对其他的压电驱动器产生机械耦合影响。因此，理论上需要使用9 个PI 迟滞模型来完全描述三个压电驱动器间的耦合迟滞效应。然而，9 个迟滞模型中需要辨识的参数过多，使其很难应用于实际的迟滞补偿当中。为了简化模型，本文设计了如图4 所示的耦合迟滞模型，其中PIk（k=1，2，3）为三个压电驱动器自身的PI 迟滞模型，而Cij（i，j=1，2，3）则为9 个恒增益量，用于表征不同压电驱动器之间的耦合效应，PI 模型中的未知量以及恒增益量后续均由辨识获得。该简化模型能够极大减少耦合迟滞模型中需要辨识的参数数量，以便于在实际应用中实现。

如图4 所示，ω（t）为耦合迟滞模型的输入，yd（t）为单个PI 迟滞模型的输出，y（t）为耦合迟滞模型的输出，它们之间的关系可以表达为：

3.3 耦合迟滞逆模型

耦合迟滞模型由三个PI 模型以及九个恒增益量表示，同理，用于补偿耦合迟滞效应的逆模型也由三个逆PI 模型以及九个逆恒增益量表示，由此耦合迟滞逆模型可以设计为如图5 所示的结构。如前文所述，PI 模型的优点之一就是便于构建逆模型，将原输入信号当做逆模型的输出信号，原输出信号当做逆模型的输入信号便可以辨识出逆模型的参数。

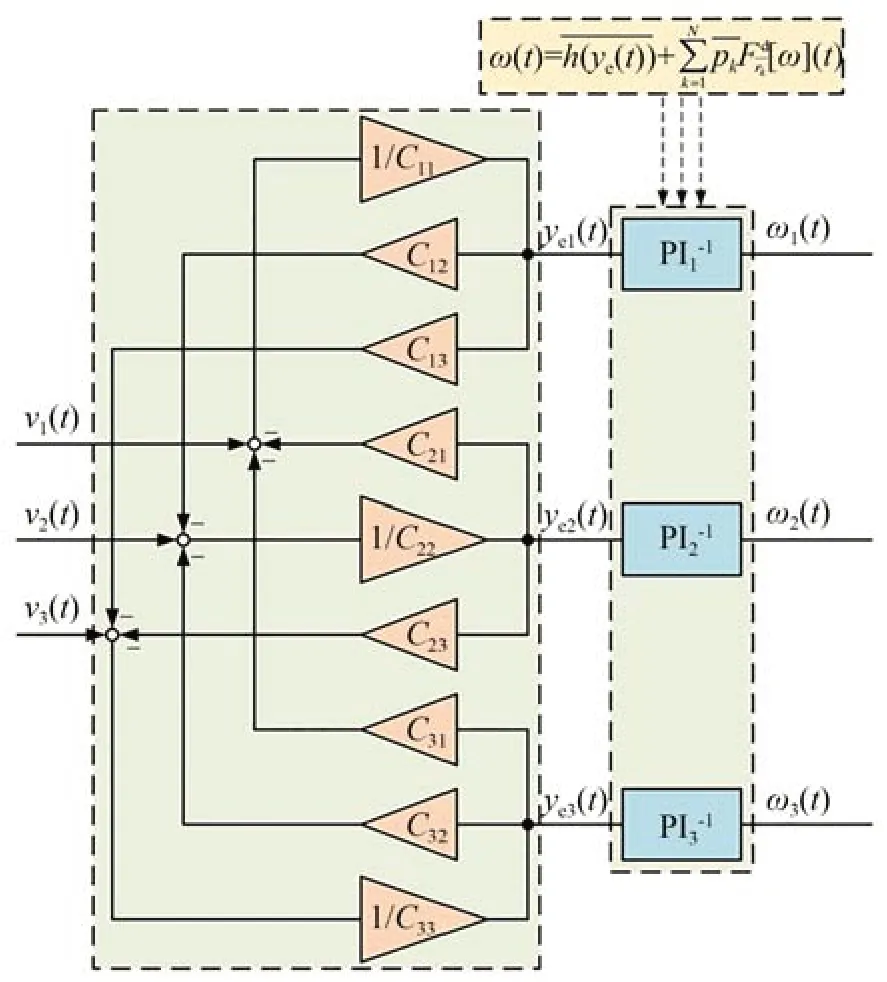
图5 耦合迟滞逆模型Fig.5 Coupled hysteresis inverse model

假设迟滞模型的输入ω（t）为迟滞逆模型的输出，ye（t）为迟滞逆模型的输入，PI 逆模型表达为：

v（t）为耦合迟滞逆模型的输入，由式（15）～式（17）可以推导得到ye（t）与v（t）的关系如下：

4 耦合迟滞模型辨识

4.1 PI 迟滞模型参数辨识

系统共有三个压电驱动器对应三个独立的PI 模型，因此需要分别辨识三组不同模型参数。以压电驱动器1 为例，首先，在开环系统中单独给定压电驱动器1 如图3（a）所示的递增三角波信号，同时由内置传感器检测得到压电驱动器实际输出位移对应的电压信号（0.05 V/μm）。然后使用Matlab 中的工具箱Optimization，将输入信号与输出信号导入，并采用如下目标函数的约束二次优化方法进行参数辨识：

其中：M1=［yd（0），yd（1），…，yd（n）］T，是模型的输出位移，n=tr/Ts，tr是输入信号的时间长度，Ts是系统采样周期，K1=［yr（0），yr（1），…，yr（n）］T是由传感器采集到的压电驱动器1 的实际位移电压信号，X=［α，β，p1，p2，…，pN，γ，η］是模型中所有需要辨识的参数。

给定Play 算子的数目等于10，由式（7）可以求出阈值rk（k=1，2，…，10）。同理，压电驱动器2 和3 的PI 模型参数也可以由如上方法辨识获得。三个压电驱动器各自的迟滞模型参数辨识结果如表1 所示。

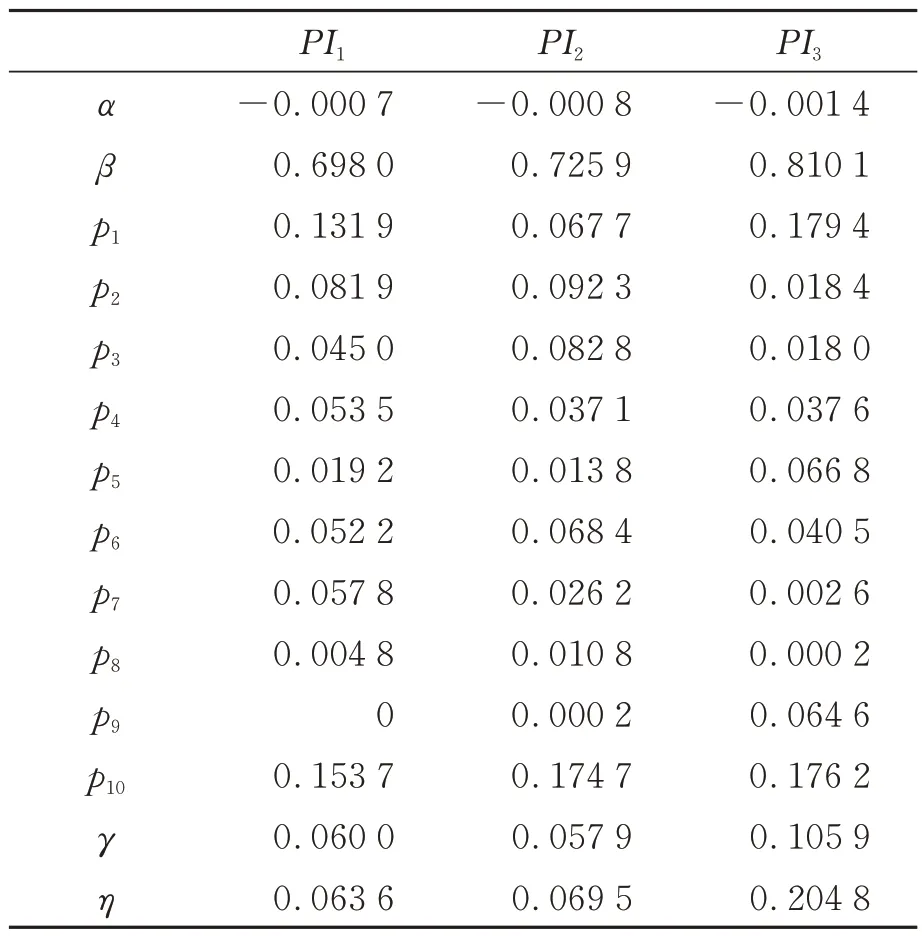
表1 PI 模型参数辨识结果Tab.1 Parameter identification results of PI model

辨识模型输出与实际输出对比如图6 所示，通过均方根误差以及最大相对误差来检查模型辨识准确性，由图6（d）可以看出，最大均方根误差小于0.5 μm，具有较高的模型辨识精度。

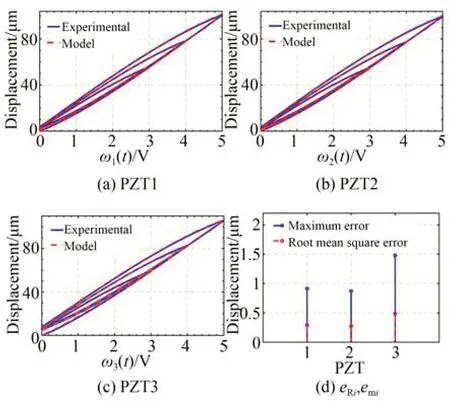
图6 PI 模型辨识结果及误差Fig.6 Identification results and errors of PI model

4.2 耦合迟滞参数辨识

每个压电驱动器对自身不存在耦合，因此设置耦合参数C11=C22=C33=1，此外，还需要确定其余的耦合参数Cij（i≠j），即每一个轴与其他轴之间的耦合都可以看作是对该轴自身迟滞模型进行线性缩小。以压电驱动器2 对压电驱动器1的耦合参数C21为例，给压电驱动器2 如图3（a）所示的驱动信号，采集到如图7 所示的压电驱动器1 耦合位移K21=［y21（0），y21（1），…，y21（n）］T。可见，由于耦合噪音很大，因此先使用高斯滤波器，平滑因子设为0.01，对耦合位移进行滤波后再进行参数辨识。然后使用Matlab 中的优化工具箱Optimization，并选用最小二乘法对耦合参数C21进行辨识，优化计算的目标函数为：

图7 压电驱动器2 对压电驱动器1 耦合参数辨识结果Fig.7 Identification results of coupling parameters of PZT 2 to PZT 1

同理，其余耦合参数也可以用上述方法进行辨识，辨识得到的耦合参数如表2 所示。

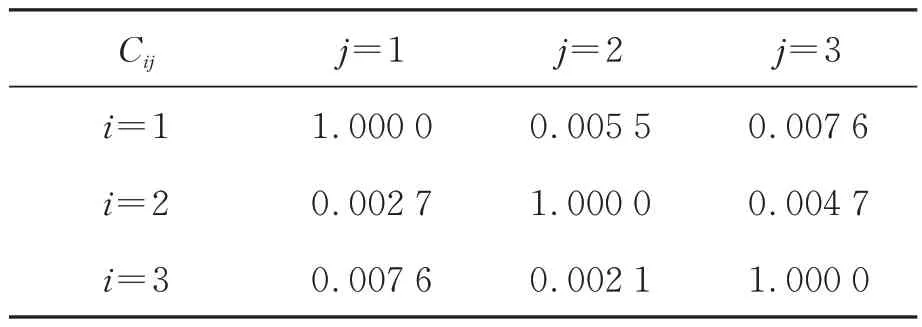
表2 耦合参数辨识结果Tab.2 Coupling parameter identification results

压电驱动器2 对压电驱动器1 产生的耦合迟滞辨识模型结果与实际输出位移对比如图7 所示，同样通过均方根误差eR来判断耦合参数辨识的准确性，结果如表3 所示，可以看出，最大均方根误差仅为0.044 μm，耦合迟滞模型参数辨识结果同样具有较高的准确度。

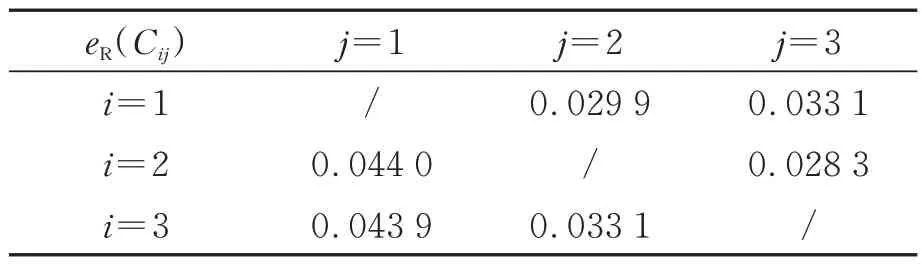
表3 耦合模型与实际耦合的均方根误差Tab.3 Root mean square error of coupling model and actual coupling（μm）

4.3 逆模型参数的辨识

由于PI 模型的可逆性，其逆模型的辨识可以参考正模型的辨识过程，只需将输入信号与输出信号互换。在开环系统中给每个压电驱动器施加如式（24）所示的输入信号：

而输出信号中的噪音会导致输入信号导数的波动，不利于参数的辨识，因此先使用五阶切比雪夫滤波器对输出信号进行平滑处理，然后将其作为输入函数，而将式（26）所示信号作为输出信号。辨识过程中，给定Play 算子的数目等于10，可由式（7）可以求出阈值rk（k=1，2，…，10），实现对逆模型参数进行辨识，辨识模型输出与实际输出对比如图8 所示，参数辨识结果如表4 所示，最大均方根误差仅为1.032 7 μm，具有较高的模型辨识精度。

表4 PI 逆模型参数辨识结果Tab.4 Parameter identification results of PI inverse model

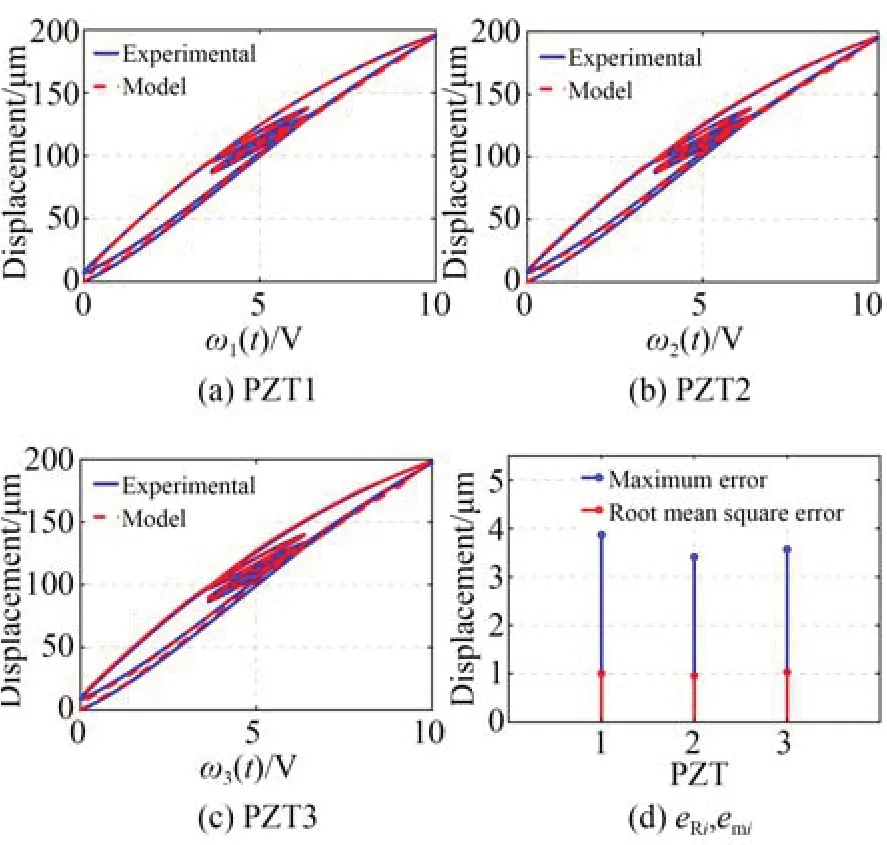
图8 PI 逆模型辨识结果及误差Fig.8 PI inverse model identification results and errors

4.4 耦合迟滞逆模型前馈补偿实验验证

为验证逆模型辨识准确性，将如图5 所示耦合迟滞逆模型开环置于压电偏摆台前方，用于补偿三个压电驱动器自身的迟滞非线性以及它们之间的耦合迟滞效应，补偿结果如图9 所示。可见，经过耦合逆迟滞模型补偿后，三个压电驱动器最大耦合位移均下降了70%～85%，同时三个压电驱动器的迟滞效应也得到了补偿，证明了所建立耦合迟滞逆模型的有效性。

5 轨迹跟踪控制

5.1 复合控制器设计

为进一步减少耦合迟滞对平台定位精度和跟踪性能的影响，设计了结合耦合迟滞逆模型前馈补偿与PID 反馈的复合控制器，控制器结构如图10 所示，该控制系统以平台三自由度末端位姿作为参考信号，经如式（4）所示运动学关系A-1变换后生成三路压电驱动器的参考信号，三路反馈信号则由压电驱动器内置传感器采集获得。

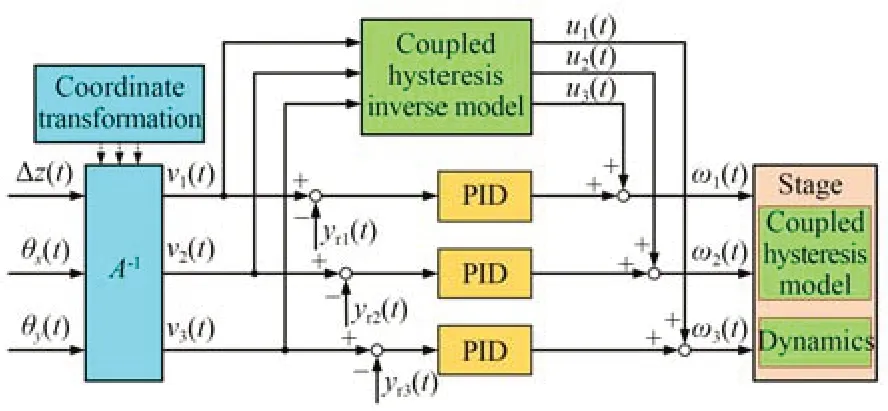
图10 耦合迟滞逆模型前馈复合控制系统Fig.10 Compound control system with coupled hysteresis inverse model feedforward

5.2 三维空间轨迹信号跟踪

利用上述复合控制器，将如式（27）所示的三维空间轨迹信号作为平台运动的参考输入，并与单独闭环控制结果进行对比，以进一步证明耦合迟滞模型以及复合控制器的有效性。

轨迹跟踪结果如图11 所示，由跟踪结果可知，复合控制下，平台偏转角度和Z 轴位移的最大均方根误差分别仅为0.06 mrad 和0.42 μm，相比单纯闭环反馈控制结果分别减小了72%和87.5%，最大误差也分别减少了76% 和83%。由此证明了本文所建立的耦合迟滞模型可以较好的提高定位精度，减少耦合及迟滞带来的影响。

6 结 论

为了解决多轴并联压电驱动纳米定位平台的耦合迟滞问题，本文以三自由度压电驱动的纳米偏摆台为对象，提出了一种可以同时描述多个压电驱动器间耦合效应及压电驱动器自身迟滞效应的耦合迟滞模型。首先将末端三自由度的运动转化为三组压电驱动器的输出。随后建立了基于PI 模型和恒增益量的耦合迟滞模型，并对该模型及逆模型进行参数辨识。耦合迟滞模型中，PI 模型表征压电驱动器自身迟滞效应，恒增益量表征压电驱动器间耦合效应。最后分别进行了开环逆模型前馈补偿实验以及结合逆模型前馈和反馈控制的球信号轨迹跟踪实验。实验结果证明，逆模型开环补偿使三个压电驱动器间的最大耦合降低了70%～85%，有效消除了平台耦合迟滞的影响，证明了所提出耦合迟滞模型的有效性。复合控制方式下，跟踪球信号时最大均方根误差仅为0.06 mrad 和0.42 μm，与逆模型补偿前相比减少了72%和87.5%，最大误差也分别减少了76%和83%，有效提升了三自由度偏摆台的定位精度。本文所提出的耦合磁滞模型也可以应用于其他类型的压电驱动多轴纳米定位平台上。