基于BP神经网络的线上线下混合式教学质量评价模型

薛 红 勤

(河南工业职业技术学院 文化旅游与国际教育学院,河南 南阳 473000)

在数字时代,传统的教学模式发生了很大变化,“教”与“学”的内涵发生了质的变化[1]。后疫情时代线上线下混合式教学模式获得了飞速的发展,众多学者对该教学模式进行了研究,并在教学模式的应用等方面取得了较多的成果[2-4]。但由于该模式在教学时间、内容分配、考核方式等方面存在很多问题,无法达到线下教学的效果,主要原因在于目前还没有系统、全面的针对该模式的客观的评估指标和方法。本文依据多指标的三维指标评价体系,利用BP神经网络的智能化分析特点,构建了一个智能化的教学质量评价模型,并对所建立的模型进行了验证,以期对未来线上线下混合式教学的发展提供帮助。

1 评价指标体系的制定

无论是线下还是线上教学,以学生为中心的理念矢志不渝,并以此构建学习理论。充分利用5G技术的发展和移动应用的普及,与移动互联网应用等新的教育形态混合并拓展,本文从课程评价、过程评价、评价主体、评价方式、评价结果五个方面提出了构建混合式教学质量评价指标体系应遵循的原则。(1)线上线下混合式教学质量评价体系应立足于教学全过程,提高教学覆盖面教学质量考核指标分。(2)线上线下混合式教学模式中的在线教学的过程评价有一定的难度,因此,更注重互动作为过程评价的重要维度。互动的方式不仅包括在线教学过程中的提问等方式互动,也包括了作业方式的互动,试卷考试测试方式的互动等。(3)线上线下混合教学模式的评价主体是教师、学生、专家和教学平台。(4)在评价方式上除线下教学中的课堂表现等,也应充分利用在线工具和应用平台的在线数据进行评价。(5)评价结果以学生的在线学习情况、作业质量、期末考试成绩等为依据,同时应注意学生课后的教学反馈及学期末的教师教学质量评价。

2 评价指标体系

教学质量评价的核心在于评价的标准,标准不同得到的结论有可能完全不同;评价标准是教师教学成绩的肯定与否。本文通过借鉴已有的研究成果[5-8],并征询相关专家意见,结合教学实践,提出线上线下混合式教学的评价指标体系。本指标体系包含了课程、教学、效果、反馈4个一级指标,20个二级指标,具体指标体系见表1。

表1 线上线下混合式教学课程建设的评价指标

3 评价方法

3.1 模型开发

线上线下混合式教学质量评价一直采用传统的评价方法,如单因素评价法、总体评价法、模糊数学、运筹学、多元统计分析、多维标量分析等,这些方法不同程度地存在以下一些问题:次要指标权重很难确定,评价具有主观性和随意性;计算复杂,求解费力;算法缺失智能算力。

生物神经网络的结构和功能被很好地模拟成人工神经网络,该方法被广泛应用于评价数学或计算模型[9]。神经网络通过连接大量的神经元构成复杂的网络结构,这种结构能具有适应性性,能依据外部信息自适应改变内部运算。因此,神经网络也是数理统计方法的实际应用,它使我们能够获得可以表达的大空间的局部结构。另一方面,神经网络可以利用数理统计的方法来解决应用中的决策问题(即统计方法让人工神经网络能够做出简单的决策)。

误差反向传播神经网络简称BP网络[10],该网络结构为三层网络前馈分层,由输入层、隐含层和输出层组成。依据误差的传播方式又可分为前向和后向传播网络。BP网络的工作模式:首先,信息从输入层发送到隐藏层的单元。隐藏单元中计算,将生成的数据发送到输出层。这种方式称为前馈方式。然后打印与期望值相比,如果不满足期望值,则转换为误差反向传播,沿着原路径传回误差,并通过修改每层神经元的连接权重来减小误差信号。通过不断的前向、后向交替的“记忆训练”,直到期望误差达到预期要求,从而得到一个稳定的网络模型。具体包括如下几个关键步骤。

(1)神经元数量的测定。模型的输入神经元数量的确定,通常是以指标体系的指标数作为神经元的数量。比如如果体系有25个子指标,那么输入层的神经元数量就定为25。

(2)输出层中神经元数量的确定。模型的输出层是混合模型最终的评估结果,可以依据评估结果来设定模型的输出层神经元数量。

(3)网络隐含层数量的确定。隐含层数量可以没有,也可以是一个或多个层。表示的含义分别是:没有隐藏层表示线性可分离函数或决策;1个隐含层表示从一个有限空间连续映射到另一个有限空间;2个隐含层可以使用有理激活函数将任意决策边界表示为任意精度,并且可以将任何平滑映射近似到任何精度;2个以上隐藏层可以学习复杂特征。

通常隐含层数量取决于输入层,输出层和输入样本的数量,本文确定隐含层数量依据下面的公式。

(1)

其中,n为输入层大小,m为输出层,s为样本量,c为常数。

(4)隐藏层中神经元数量的测定。

通过网络的收敛性来判定隐藏层中的神经元数量。隐藏层的神经元多少都会带来性能问题,太少会使得训练不充分,造成网络不够“鲁棒”,容错率降低;相反,神经元太多训练时间长,性能降低,误差也提高不了多少。因此,神经元参数确定大多采用遗传算法,或者粒子算法来寻找最优的参数,最终得到一个经验公式来确定。以下方程是几个广泛使用的经验公式。

s=(0.43mn+0.12m2+2.54n+0.77m+0.35)1/2+0.51

(2)

s=(m+n)1/2+a,a∈[1,10]

(3)

(4)

其中,n为输入层大小,m为输出层,s为样本量,c和a为常数。

(5)神经元转换函数。BP神经网络神经元转换函数种类有很多,比如:Sigmoid函数、HardSigmoid函数、Swish函数、ReLU函数等。其中Sigmoid函数表达式如公式(5)所示。

(5)

其中系数λ表示函数的压缩程度。

(6)模型结构及训练流程。由上述参数确定后的基于BP神经网络线上线下混合式教学质量评价模型的结构如图1所示。构建的神经网络训练流程如图2所示。

3.2 模型训练及测试

针对所构建的线上线下混合式教学质量评价模型,需要进行训练及测试,模型数据来源于学校一门课的期末考试及调查问卷,调查对象包括本专业所有参考学生,调查指标涵盖模型所有指标,要求学生对所有指标进行评分,总共78份,最终有效数据为60份。训练数据和测试数据按照2∶1分配,40份作为训练数据,20份为测试数据。神经元数量参数设置为 输入层∶隐含层∶输出层=38∶12∶1,学习率η=0.90,目标误差为ε=0.001。

网络训练完成后,利用测试数据进行测试。将测试模型输出值与真实值进行比较,比较数据如表2所示,真实值和模型输出值的误差对比图如图3所示。通过误差分析可以看出,构建的线上线下混合式教学质量评价模型的输出值与真实值比较接近,误差在可接受范围。由此,该模型的评价指标能较为准确地反映教学效果,具有一定的参考价值。

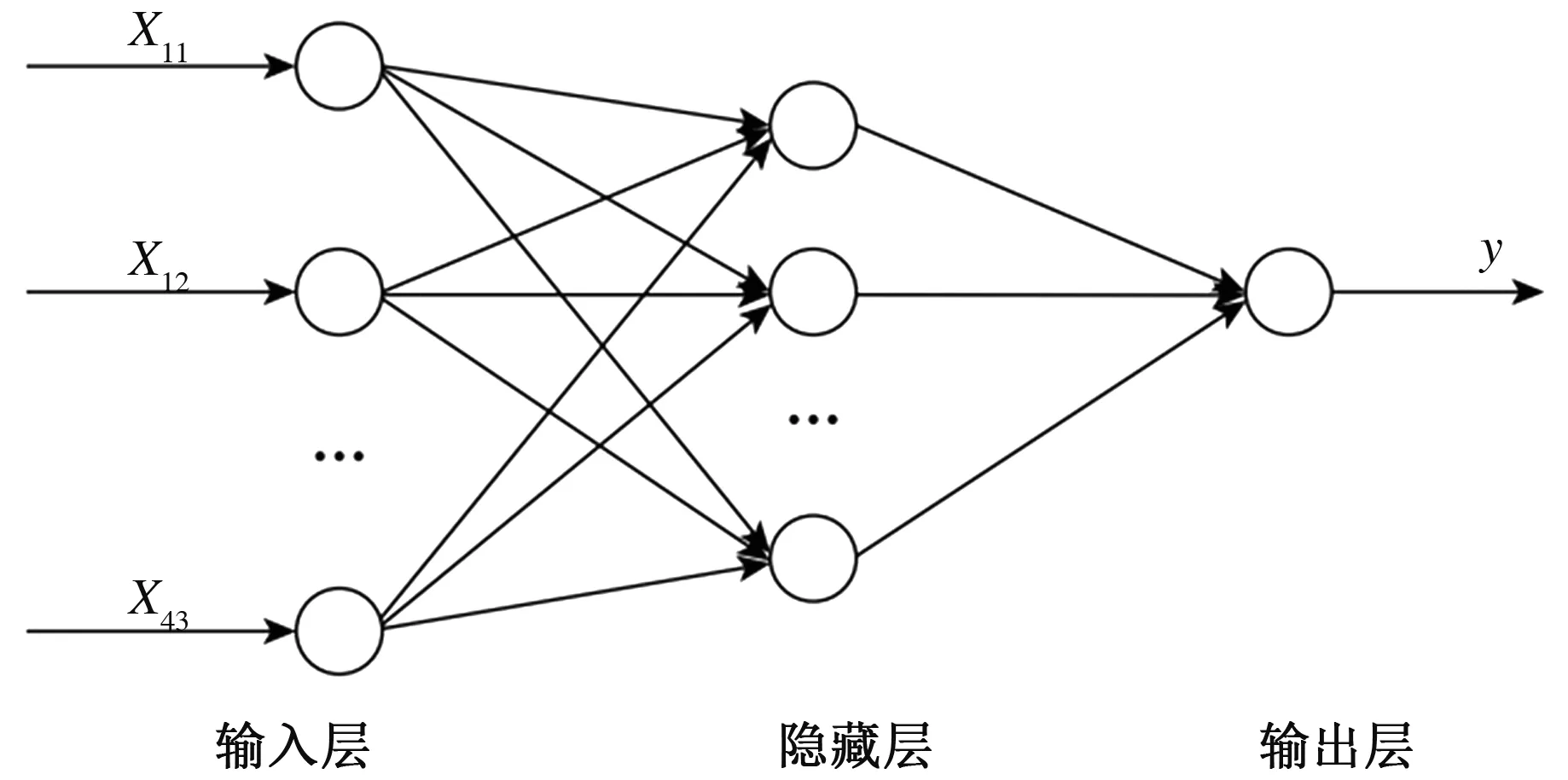
图1 BP模型评价结构

图2 训练流程图

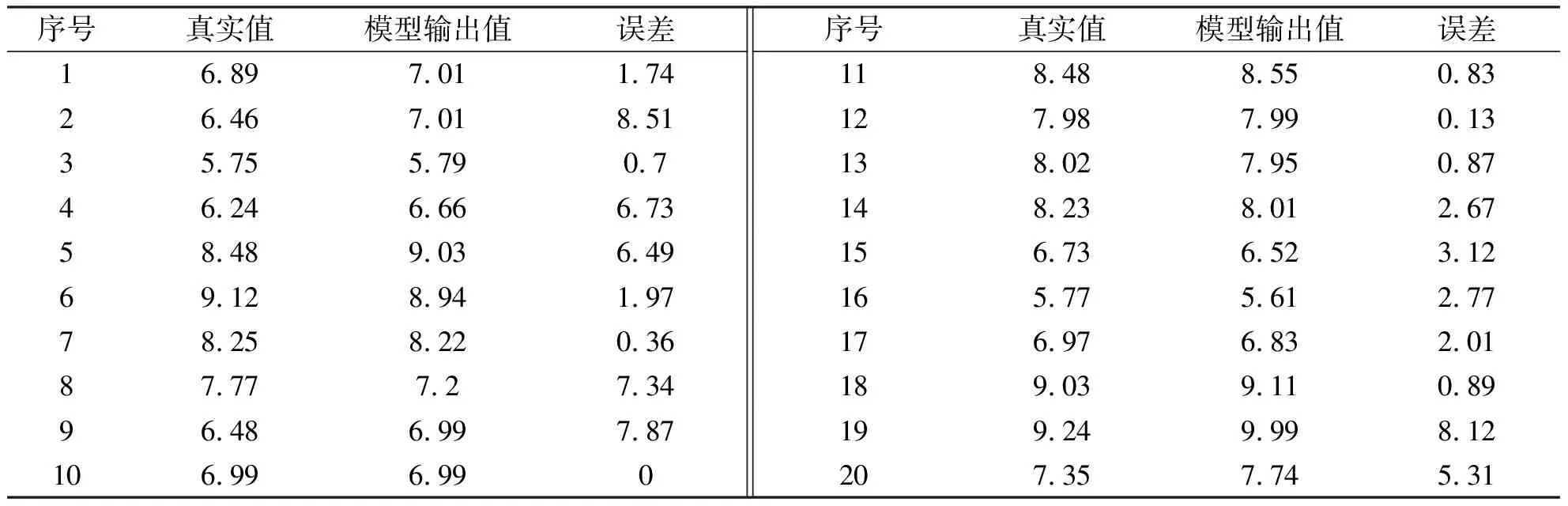
表2 真实值与模型测试结果

图3 真实值和模型输出值图

该模型在迭代过程中从开始到结束的收敛速度都很快,具有良好的并行效果。在测试组数据时,准确率高达82.36%。在BP模型训练中,相对传统模型同比增长6.30%,精度明显更高。由此对比传统模型,本文的BP神经网络模型提高了线上线下混合式教学质量评价训练效果,更快的计算时间,更快的收敛速度,提高了准确率,且误差非常小,完全在可接受的范围内。

4 结论

经过实证研究,该模型的输出值与真实值之间的误差在可接受范围,性能基本可以满足实际的评价需求。另外,模型的精度取决于训练样本的数量,随着模型的应用,训练样本的增加,精度会逐步提高。总之,基于神经网络构建的线上线下混合教学质量评价模型为教学质量评价和改进方案提供有益的参考。未来,评价模型可以通过引入大数据和深度学习来进一步改进。此外,应利用更多的案例来进一步验证所制定的指标体系和评价模型。