混合超级半爱因斯坦流形

杨永举, 张振宇, 王学强

(1.南阳师范学院 数学与统计学院,河南 南阳 473061; 2.河南省社旗县饶良镇黄桥小学,河南 社旗 473300)

0 引言

Chaki 和Ghosh 在文献[1]中引入了半爱因斯坦流形的概念:如果一个非平坦的n维黎曼流形的非恒为0的Ricci曲率S(X,Y)满足:S(X,Y)=ag(X,Y)+bA(X)A(Y),a,b(b≠0)为常数,A为非零一阶微分形式,U为对应A的单位向量场,即g(X,U)=A(X),g(U,U)=1,则称此流形为半爱因斯坦流形。由于此类流形在物理学相关问题研究中有重要价值。随后此概念被不断地推广,如: M.C.Chaki在文献[2]中引进通常半爱因斯坦流形,符号为G(GE)n;A.Bhattacharya,M.Tarafdar and D.Debnath在文献[3]中引进混合超级半爱因斯坦流形,符号为MS(GE)n;M.C.Chaki在文献[4]中引进超级半爱因斯坦流形,符号为S(GE)n;A.A.Shaikh在文献[5]中引进拟半爱因斯坦流形,符号为P(GE)n。P.Debnath and A.Konar在文献[6]中引进并探讨了混合超级半爱因斯坦流形,它的定义为:如果一个非平坦黎曼流形的非恒为0的Ricci曲率S(X,Y)满足下面式子:

S(X,Y)=ag(X,Y)+bA(X)A(Y)+c[A(X)B(Y)+A(Y)B(X)]+dB(X)B(Y)+fD(X,Y),

(1)

其中a,b,c,d,f为全不为0的常数,A,B为两个一阶微分形式,U,V为分别对应于微分形式A,B的单位向量场,且满足

g(X,U)=A(X),g(X,V)=B(X),g(U,V)=0,

(2)

标记此类流形为MS(QE)n, 称U为此流形的生成元,

D(X,U)=0,traceD=0。

(3)

本文探讨了在局部分数阶导数定义下的混合超级半爱因斯坦流形,即混合超级半爱因斯坦分形流形,得出其在分形空间上的若干结论。

1 预备知识

局部分数阶微积分是处理康托集中出现的各种不可微问题,局部分数阶微积分也是纯数学中的一个重要工具。在本节中,我们将介绍局部分数阶微积分的基本概念:连续性、导数和积分。依据有关参考文献,我们直接引入分形空间上的若干分形几何定义与定理。

定义1[7-8]在分形空间中,连续函数Θ(t)在t=t0处的α阶导数定义为

(4)

其中,Δα(Θ(t)-Θ(t0))≅Γ(1+α)Δ(Θ(t)-Θ(t0))。

定义2[7-8]分形空间上连续函数Θ(t)在区间[c,d]的α阶积分定义为

(5)

其中,Δtj=tj+1-tj,Δt=max{Δt1,Δt2,…,Δtj}和[tj,tj+1],j=0,…,N-1,t0=c,tN=d, 是区间[c,d]的分割。

定义3[8]局部分数阶黎曼空间中,任意两点yiα=yiα(e1α,e2α,e3α,…,eNα)和yiα+dαyi之间的局部分数阶度量由下式确定:

(6)

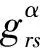
定理1[10]如果共形平坦的流形(Mn,g),n≥3的(0,4)型黎曼张量场满足如下条件:

R(X,Y,Z,W)=E(Ric(Y,W)Ric(X,Z)-Ric(X,W)Ric(Y,Z))+F(g(Y,Z)g(X,W)-g(X,Z)g(Y,W)),则(Mn,g),n≥3局部等距浸入到分形空间R(n+1)α中。

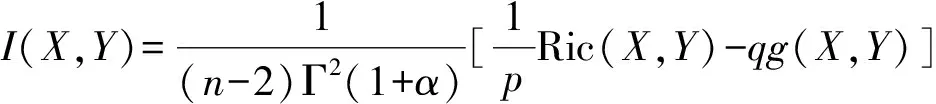
2 主要定理及结论

2.1 定义在分形空间上的平坦流形与混合超级半爱因斯坦分形流形

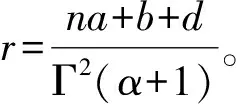
引理2 混合超级半爱因斯坦分形流形MS(QE)n的生成元U如果为平行向量场,则a+b=0,c=0。

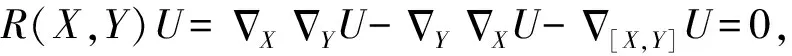
定理2 共形平坦混合超级半爱因斯坦分形流形MS(QE)n,n≥3如果满足条件:

〈Ⅲ〉a>0,(2-n)a+b+d>0,

则(Mn,g)局部等距浸入到分形空间R(n+1)α中。

证明：共形平坦的(0,4)型黎曼张量R(X,Y,Z,W)可以表示为:

其中,r为流形的数量曲率。

如果流形为混合超级半爱因斯坦分形流形,利用式子(1),可以知道

(7)

由于

Ric(X,W)Ric(Y,Z)=a2g(X,W)g(Y,Z)+abg(X,W)A(Y)A(Z)+acg(X,W)B(Y)B(Z)+

adg(X,W)[A(Y)B(Z)+B(Y)A(Z)]+aeg(X,W)D(Y,Z)+abg(Y,Z)A(X)A(W)+

b2A(X)A(Y)A(Z)A(W)+bcA(X)A(W)B(Y)B(Z)+bdA(X)A(W)[A(Y)B(Z)+A(Z)B(Y)]+

beA(X)A(W)D(Y,Z)+acg(Y,Z)B(X)B(W)+bcA(Y)A(Z)B(X)B(W)+c2B(X)B(Y)B(Z)B(W)+

cdB(X)B(W)[A(Y)B(Z)+A(Z)B(Y)]+ceB(X)B(W)D(Y,Z)+

adg(Y,Z)[A(X)B(W)+A(W)B(X)]+bdA(Y)A(Z)[A(X)B(W)+A(W)B(X)]+

cdB(Y)B(Z)[A(X)B(W)+A(W)B(X)]+d2[A(X)B(W)+A(W)B(X)][A(Y)B(Z)+A(Z)B(Y)]+

edD(Y,Z)[A(X)B(W)+A(W)B(X)]+aeg(Y,Z)D(X,W)+beA(Y)A(Z)D(X,W)+

ceB(Y)B(Z)D(X,W)+edD(X,W)[A(Y)B(Z)+A(Z)B(Y)]+e2D(X,W)D(Y,Z)。

(8)

同样,也可以写出Ric(Y,W)Ric(X,Z)的表示式。

Ric(Y,W)Ric(X,Z)=a2g(Y,W)g(X,Z)+abg(Y,W)A(X)A(Z)+acg(Y,W)B(X)B(Z)+

adg(Y,W)[A(X)B(Z)+B(X)A(Z)]+aeg(Y,W)D(X,Z)+abg(X,Z)A(Y)A(W)+

b2A(X)A(Y)A(Z)A(W)+bcA(Y)A(W)B(X)B(Z)+bdA(Y)A(W)[A(X)B(Z)+A(Z)B(X)]+

beA(Y)A(W)D(X,Z)+acg(X,Z)B(Y)B(W)+bcA(X)A(Z)B(Y)B(W)+c2B(X)B(Y)B(Z)B(W)+

cdB(Y)B(W)[A(X)B(Z)+A(Z)B(X)]+ceB(Y)B(W)D(X,Z)+

adg(X,Z)[A(Y)B(W)+A(W)B(Y)]+bdA(X)A(Z)[A(Y)B(W)+A(W)B(Y)]+

cdB(X)B(Z)[A(Y)B(W)+A(W)B(Y)]+d2[A(Y)B(W)+A(W)B(Y)][A(X)B(Z)+A(Z)B(X)]+

edD(X,Z)[A(Y)B(W)+A(W)B(Y)]+aeg(X,Z)D(Y,W)+beA(X)A(Z)D(Y,W)+

ceB(X)B(Z)D(Y,W)+edD(Y,W)[A(X)B(Z)+A(Z)B(X)]+e2D(Y,W)D(X,Z)。

(9)

根据式子(1)(7)(8)(9)结合定理条件可得

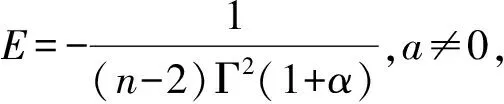
由上所述,根据定理1,可知定理结论成立。

评注：当n=3或者4时,是满足该定理条件的MS(QE)n的非平凡情况,即:使a,b,c,d,f为全不为0条件下的MS(QE)n是不存在的。

证明：如果MS(QE)n共形平坦,那么(0,4)型黎曼曲率张量R(X,Y,Z,W)为:

实际上,

(10)

其中,D(X,Y)=g(QX,Y)。

利用式子(1)(2)(3)和(10)且令Z=U,可得

(11)

如果U为平行向量场,根据引理2可知,a+b=0,c=0,所以上式(11)可化为

定理4 上调合平坦MS(QE)n流形的生成元U,如果为平行向量场,则Ric(V,V)=0。

证明：由于MS(QE)n上调合平坦,故

事实上

(12)

如果U为平行向量场,根据引理2可知a+b=0,c=0,所以上式(12)可化为

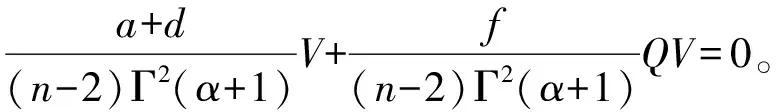
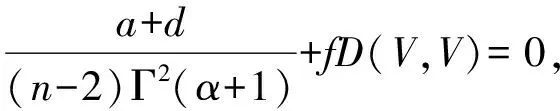
定理5 投影平坦且生成元U为平行向量场的MS(QE)n的数量曲率r=0。

证明：如果MS(QE)n投影平坦,那么(0,4)型黎曼曲率张量R(X,Y,Z,W)为

(13)

对(13)式进行缩并且令W=U,可得bA(X)=0,所以b=0。根据引理1可知a+b=0,c=0可得a=b=0,所以

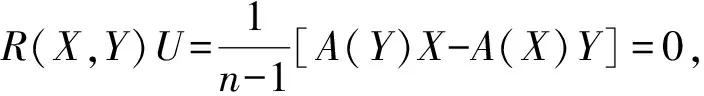
S(X,Y)=fD(X,Y),根据式子(3)可知数量曲率r=0。

2.2 局部共形 Kähler 流形与混合超级半爱因斯坦分形流形

定理6 具有平行lee形式的紧致,定向,无边的连通非Kähler 的局部共形Kähler 流形,同时也是MS(QE)n型流形,其黎曼Ricci曲率S(X,Y)表示为:

S(X,Y)=ag(X,Y)+bA(X)A(Y)+c[A(X)B(Y)+A(Y)B(X)]+dB(X)B(Y)+fD(X,Y),

其中,A,B分别为lee形式和反lee形式,U,V为分别对应于A,B的单位lee向量场和单位反lee向量场,则U平行向量场当且仅当a+b=0。

证明：充分性由引理2显然可知。下证必要性。

定理7 如果一个具有平行lee形式的紧致连通非Kähler 的局部共形Kähler 流形(Mn,g)(n≥2),同时也是MS(QE)n型流形,其黎曼Ricci曲率S(X,Y)表示为:

S(X,Y)=ag(X,Y)+bA(X)A(Y)+c[A(X)B(Y)+A(Y)B(X)]+dB(X)B(Y)+fD(X,Y),

其中A,B分别为lee形式(平行)和反lee形式,U,V为分别对应于A,B的单位lee向量场和单位反lee向量场。设r为数量曲率,则

(2)(Mn,g)不为上调和平坦流形,也不为投影平坦流行。

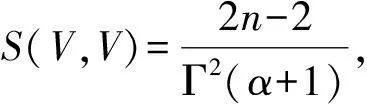
S(X,Y)=ag(X,Y)+bA(X)A(Y)+c[A(X)B(Y)+A(Y)B(X)]+dB(X)B(Y)+fD(X,Y),因此

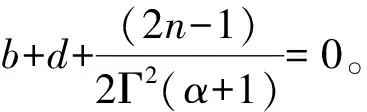
由此方程组整理可得

(14)

2.3 混合超级半爱因斯坦流形的一些整体性质

定理8 设紧致,定向,无边界的MS(QE)n型流形满足:b,c,d,f≥0,a+b+c+d+f≤0,那么投影killing向量场X的协变导数为0,如果b,c,d,f>0,a+b+c+d+f<0,那么此类流形不存在非零的投影killing向量场。

证明：参考文献[11]知,投影killing向量场X满足

ξ为向量场X对应的一形式,由文献[13]可知S(X,X)≤0,则由前述等式可以知道dξ=0,divX=0。即证X为调合向量场,又为投影killing向量场。因此其协变量导数为0。

定理9 设紧致,定向,无边界的MS(QE)n型流形满足:b,c,d,f>0,a+b+c+d+f<0,那么此类流形不存在非零的共形killing向量场。

本文尝试讨论局部分数阶导数定义下的混合超级半爱因斯坦流形,我们觉得在分形多孔空间上讨论混合超级半爱因斯坦流形是一个有趣的问题。