涉及零点个数的亚纯函数的正规定则

陈鹏斌, 杨 祺

(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)

1 引言和主要结果

设F是区域内的一族亚纯函数,如果对于F中的任一族子列{fn},存在子序列{fnj}在区域内按球距内闭一致收敛于亚纯函数(或者∞),则F在区域上正规[1-3]。

1979年顾永兴在文献[4]中证明了Hayman猜想,得到以下结果。

定理A[4]设F为区域内一亚纯函数,k为正整数,若对于任意f(z)∈F,有f(z)≠0,f(k)(z)≠1,则F在区域中正规。

杨乐在文献[5]中改进了定理A,证明了如下结论。

定理B[5]设F为区域内一亚纯函数族,k是一正整数,h(z)是区域内不恒为0的全纯函数,若对于任意f(z)∈F,如果f(z)≠0,并且f(k)(z)≠h(z),则F在区域内正规。

常建明在文献[6]中把定理A中的“f(k)(z)≠1”换成“f(k)(z)=1”,并且限制零点的个数,证明下面定理。

定理C[6]设F为区域内一族非零亚纯函数,k为正整数,若对于任意f(z)∈F,f(k)(z)-1至多有k个不同零点, 则F在区域中正规。

刘丹在文献[7]中推广了定理B和定理C,得到如下结论。

定理D[7]设F为区域内一族非零亚纯函数,k是一正整数,h(z)(≢0)是区域的全纯函数,若对于任意f(z)∈F,f(k)(z)-h(z)至多有k个不同零点,则F在区域内正规。

邓炳茂等人在文献[8]中将h(z)是区域内不恒为0的全纯函数换为h(z)是区域内不恒为0的亚纯函数,得到如下定理。

定理E[8]设F为区域内一族非零亚纯函数,k,m是一正整数且m≤k,h(z)(≢0)是区域内的亚纯函数且所有极点重级至多为m,若对于任意f(z)∈F,f(k)(z)-h(z)至多有k-m个不同零点(不计重数),则F在区域内正规。

一个自然的问题,能否将定理D和定理E中“f(k)(z)”推广到f的微分多项式,本文研究这一问题,得到如下结果。

定理1设F为区域内一族非零亚纯函数,k是正整数,h(z)(≢0)在区域内全纯函数。若对于∀f∈F,L(f)-h(z)至多有k个不同零点,其中L(f)=f(k)(z)+a1(z)f(k-1)(z)+…+ak(z)f(z)是关于f的微分多项式,ai(z)(i=1,2,…,k)是区域内全纯函数,则F在区域上正规。

定理2设F为区域内一族非零亚纯函数,k,m是正整数且m≤k,h(z)≢0在区域内亚纯函数且所有极点重级至多为m。若对于∀f∈F,L(f)-h(z)至多有k-m个不同零点(不计重数),其中L(f)=f(k)(z)+a1(z)f(k-1)(z)+…+ak(z)f(z)是关于f的微分多项式,ai(z)(i=1,2,…,k)是区域内全纯函数,则F在区域上正规。

2 引 理

为证明本文结果,需要下列4个引理。

引理1[9-10]设F为区域内一族非零亚纯函数族,α∈R且满足-1<α<∞,若F在z0∈不正规,则存在

(1)点列zn,zn→z0;

(2)函数列fn∈F;

(3)正数列ρn→0+,

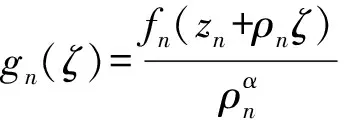
引理2[11]设f是超越亚纯函数,a(z)为不恒为0的多项式,k是正整数。若对于任意f(z)≠0,则f(k)(z)-a(z)有无穷多个零点。

引理3[6]设f是非常数有理函数,k是正整数。若对于任意f(z)≠0, 则f(k)(z)-1至少有k+1个不同零点(不计重数)。

引理4[7]设f是非常数有理函数,a(z)为不恒为0的多项式,k是正整数。若对于任意f(z)≠0,则f(k)(z)-a(z)至少有k+1个不同零点(不计重数)。

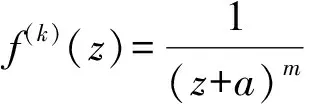
引理6设F={fn}是区域内的一族亚纯函数,k是正整数,{φn}是区域内的一列全纯函数并且φn(z)→φ(z)(≠0),若对于∀fn∈F,fn≠0,并且P(fn)(z)=φn(z)至多有k个不同零点(不计重数),其中是关于f的微分多项式,ai(z)(i=1,2,…,k)是区域内全纯函数,{βn}为有界量,则F在区域上正规。

证明：假设F在z0∈不正规,由引理1可知,存在点列zn→z0,函数列fn(z)∈F,正数列ρn→0+使得在复平面上按球距内闭一致收敛于非常数亚纯函数g(ξ),并且g(ξ)≠0。

断言:g(k)(ξ)-φ(z0)至多有k个不同零点。

事实上,假设g(k)(ξ)-φ(z0)有k+1个不同零点ξj(1≤j≤k+1),显然,g(k)(ξ)≢φ(z0)。由于

所以就有

因此由引理2可知:g(ξ)为有理函数,从而又与引理3矛盾。因此F在z0处正规。故F在区域上正规。

3 定理的证明

定理1证明不妨设={z:|z<1|}。设z0为内任意一点,以下证明F在z0处正规即可。分两种情况讨论:

断言:g(k)(ξ)-1至多有k个不同零点。

事实上,假设g(k)(ξ)-1有k+1个不同零点ξj(1≤j≤k+1),显然,g(k)(ξ)≢1。由于

所以就有

因此由引理2可知:g(ξ)为有理函数,从而与引理3矛盾。因此F在z0处正规。

情形2若h(z0)=0。不妨设z0=0,h(z)=zm+am+1zm+1+…=zmb(z),其中m≥1,b(0)=1,且当0<|z|<1时,h(z)≠0。令

因为对任意的f∈F,f(z)≠0,所以对任意F∈H,F(z)≠0,且0是F(z)的m重极点。

若H在z=0处不正规,则由引理1可知,存在点列zn→0,函数列Fn(z)∈H,正数列ρn→0+使得

以下分两种情况讨论:

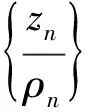
并且可知

所以就有

又因为由定理条件可知:在Δ(0,δ)={z:|z|<δ}内L(f)(z)-h(z)至多有k个不同零点,所以G(k)(ξ)-ξm在复平面上至多有k个不同零点。这时由引理2可知:G(ξ)为有理函数,从而与引理3矛盾。

⋮

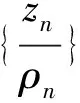
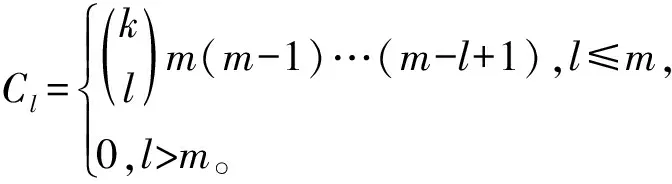
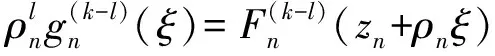
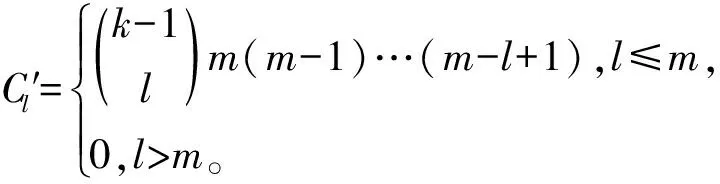
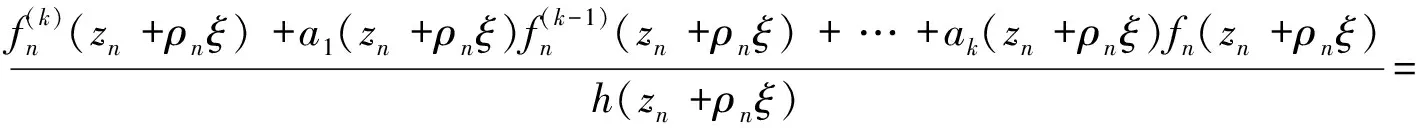
可知

又因为f(z)≠0。并且L(f)(z)-h(z)在区域内至多有k个不同零点。与情形1讨论类似,可知,g(z)≠0,并且g(k)(ξ)-1在复平面上也至多有k个不同零点。这时由引理2可知,g(z)为有理函数,从而与引理4矛盾,所以可知H在z=0处正规。

所以由最大模及Montel正规定则可知,F在z=0处正规,则F在区域上正规。

定理2证明由正规局部性及定理1可知,我们只需证明F在h(z)的所有极点正规即可。不失一般性,不妨设=Δ,并且

其中,m≥1,b(0)=1,且在0<|z|<1内b(z)≠0,∞。以下只需证明F在z=0处正规。

假设F在z=0处不正规,则由引理1可知:取α=k-m,存在点列zn→0,正数列ρn→0+,函数列fn∈F,使得

下面分两种情况讨论:

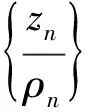
由于fn(z)≠0且m≤k,所以Fn(z)≠0。下面证明{Fn(ξ)}在Δ内正规。

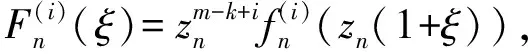
则

即

所以存在{Fn(ξ)}的子列{Fnj(ξ)}和亚纯函数F(ξ),满足

若F(0)≠∞,则

从而意味着g(k-m)(ξ)为常数,因此g是一个多项式,从而与g(ξ)是一个非常数非零亚纯函数矛盾。

若F(0)=∞,则

所以与g(ξ)是非常数亚纯函数矛盾。

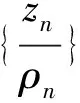
可得,就有

即

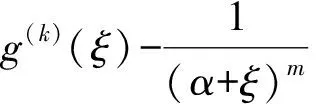
故由引理2可知:g(ξ)为有理函数。继续由引理4可知,g(ξ)为常数,矛盾。因此F在z=0处正规。

综上可知:F在区域内正规。