Benchmarking calculations of excitation energies and transition properties with spectroscopic accuracy of highly charged ions used for the fusion plasma and astrophysical plasma

Chunyu Zhang(张春雨), Kai Wang(王凯), Ran Si(司然), Jinqing Li(李金晴),Changxian Song(宋昌仙), Sijie Wu(吴思捷), Bishuang Yan(严碧霜), and Chongyang Chen(陈重阳),§

1Shanghai EBIT Laboratory,Key Laboratory of Nuclear Physics and Ion-beam Application,Institute of Modern Physics,Department of Nuclear Science and Technology,Fudan University,Shanghai 200433,China

2Department of Physics,University of Strathclyde,Glasgow G4 0NG,UK

3Department of Physics and Anhui Key Laboratory of Optoelectric Materials Science and Technology,Key Laboratory of Functional Molecular Solids,Ministry of Education,Anhui Normal University,Wuhu 241000,China

4Hebei Key Laboratory of Optic-electronic Information and Materials,The College of Physics Science and Technology,

Hebei University,Baoding 071002,China

Keywords: energy levels, transition rates, highly charged ions, relativistic many-body perturbation theory(RMBPT),multi-configuration Dirac–Hartree–Fock(MCDHF),benchmarking calculations,excitation energies,spectroscopic accuracy

1.Introduction

The ions withZ ≤30, especially the ions of iron group elements, produce several strong transitions that have been widely used in astrophysics for a range of diagnostic applications, e.g., measuring electron temperatures, densities, chemical composition,and even strong magnetic fields,[1]for a review of some of the applications, see Del Zanna & Mason.Providing accurate atomic data for these ions is of paramount importance.In the tokamak fusion reactors, such as ITER[2]and EAST,[3,4]tungsten is an element proposed to be used as an erosion-resistant construction material.Therefore, highlycharged tungsten ions are of great interest in fusion plasma research.[5–9]The core temperature of ITER is projected to be of the order of 20 keV,possibly reaching as high as 30–40 keV under certain operating conditions.[10,11]At this temperature,highly-charged tungsten ions, with openL-shell,M-shell, orN-shell,have a large fractional abundance in the core plasma.The x-ray and extreme ultraviolet(EUV)spectra emitted from these tungsten ions, therefore, constitute the solid base of diagnostics for ITER plasma properties(such as temperature and density) and the bulk velocity of the plasma core.[8,12]Additionally,krypton is widely used as an injected impurity for diagnosing tokamak fusion plasmas,[13–17]and is also used as a diagnostic element for the x-ray imaging spectrometer system in the ITER.[18,19]

Atomic data such as excitation energies,transition wavelengths,radiative rates,and level lifetimes with high precision are necessary for plasma diagnostics and for interpreting the plasma spectra.Experiments with their limited resources are unlikely to ever be able to provide complete datasets on any atomic systems.Instead,the bulk of the data must be provided by theoretical calculations.Based on fundamental principles and well-justified approximations, theoretical atomic physics derives and implements algorithms and computational procedures that yield the desired data.

The atomic spectroscopy group of Fudan University has mainly carried out two projects in collaboration with other groups in the past decade.One project focuses on the ions withZ≾30 that are generally of astrophysical interest, and the other one is about krypton (Z= 36) and tungsten ions (Z= 74) that are relevant in research of magnetic confinement fusion.Employing the multiconfiguration Dirac–Hartree–Fock (MCDHF) approach[20,21]implemented in the GRASP2K package,[22]and/or the relativistic manybody perturbation theory (RMBPT)[23–25]or relativistic configuration interaction (FAC-RCI)[26]implemented within the FAC package,[27,28]a large amount of atomic data including level energies, transition wavelengths, line strength, oscillator strengths,radiative rates and level lifetimes were obtained.By using the two different and independent methods(MCDHF and RMBPT), we cross-check/validate our two datasets and guarantee the self-consistency of our theoretical calculations.Additionally,by detailed comparisons with available accurate observations and theoretical calculations in the literature, we comprehensively assess the uncertainties of our calculations(see the summary in Section 4).The high accuracy of our systematic calculations makes them the preferable source of spectroscopic data for modelling plasma spectra and opens up new possibilities for their usage for the calibration of experimental x-ray and extreme ultraviolet(EUV)spectra.

The paper is organized as follows.The MCDHF and RMBPT methods are outlined in Section 2.In Subsection 3.1, we review the results from recent accurate RMBPT and MCDHF calculations forK-,L-, andM-shells ions withZ ≤42.In Subsection 3.4, we review our previous works for tungsten ions with openM-shell and openN-shell, and present and discuss our complete RMBPT and MCDHF calculations for the excitation energies,electric dipole(E1),magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transition properties, and level lifetimes for the lowest 148 levels belonging to the 3l3configurations in Al-like W61+.The conclusions and outlook are shown in Section 4.If not explicitly indicated, atomic units are used throughout this work.

2.Outline of theory

2.1.MCDHF

The MCDHF method[20,21]implemented in the GRASP2K package[22]has been discussed in our recent studies.[29,30]Here, we only give a brief description.The MCDHF method starts from the Dirac–Coulomb(DC)Hamiltonian

whereVnuc(ri) is the nuclear potential,riis the electron–nucleus distance,rijis the distance between electronsiandj,cis the speed of light,Nis the number of electrons,andαiandβidenote the Dirac matrices.

Electron correlation is included by expanding the atomic state wave function(ASF)Ψ(Γ Jπ)in a linear combination of configuration state functions(CSFs)

where{γi}specifies the occupied subshells with their complete angular coupling tree information of the CSFs,Jandπare respectively the total angular momentum and the parity, andMis the number of CSFs.Each CSF,Φ(γiJπ),is aj j-coupled many-electron function built from antisymmetrized products of one-electron Dirac orbitals.[20]The radial functions of the large and small components of the oneelectron Dirac orbitals and the expansion coefficients{ci}of the CSFs are obtained by solving iteratively the relativistic self-consistent field (RSCF) radial equations for the orbitals,coupled to the matrix diagonalization for the targeted eigenvectors.

Once the orbitals have been optimized through the MCDHF procedure, the Breit interaction and higher-order(HO) retardation correction beyond the Breit interaction, as well as the leading quantum electrodynamic(QED)effects including self-energy (SE) and vacuum polarization (VP), are added to the Dirac–Coulomb Hamiltonian in the RCI calculations to capture relativistic corrections to the Coulomb interaction(see Refs.[29,30]for more details).

It should be noted that the SE correction is evaluated with a model QED operator developed recently by Shabaevet al.[31,32]It has been implemented in GRASP2K to study the ground-term fine structures of F-like[33]and Co-like ions,[34]and was also used in our recent benchmark works on W56+–W61+.[29,30]The SE correction is determined by evaluating the matrix element of the model self-energy operator

2.2.RMBPT

The RMBPT method[23–25]is implemented in FAC.[27,28]This method is based on an approximation of the Dirac–Coulomb–Breit (DCB) HamiltonianHDCB=HDC+HBreit.Then theHDCBoperator is split into a zeroth-order model HamiltonianH0and a perturbationH′, i.e.,HDCB=H0+H′,with[23,28]

wherehD(i)is the Dirac Hamiltonian for one free electron,Zis the nuclear charge,riis the radial coordinate of the electroni, andrijis the distance between the electronsiandj.Bijis the frequency-independent Breit interaction.U(ri) is a oneelectron model potential including the screening effects of all electrons,whose appropriate choice makesH′as small as possible.U(ri)is approximated by a local central potential and is derived from a Dirac–Fock–Slater self-consistent field calculation with the HamiltonianH0,which minimizes the weighted mean energy of all relevant configurations.AfterU(ri)is determined,the eigenfunctionsΦ0kand eigenvaluesE0kofH0can be calculated.TheΦ0kis divided into a model spaceMand the orthogonal spaceN.The effect of the states outside theMspace is as usual taken into account by means of a perturbation expansion and expressed in terms of an “effective” HamiltonianHeffthat operates only within theMspace.Heffis defined as

wherePis a projection operator that produces a stateΨ0kin theMspace when it operates on an eigenfunctionΨkof the full Hamiltonian,whereΨ0kis a linear combination of the subset ofΦ0kthat belongs to theMspace.Ωis the wave operator that transformsΨ0kback toΨk.The eigenvalues ofHeffare the true eigenenergies of the full Hamiltonian.

The matrix element of the first-orderHeffcan be written as

where (HDCB)ij=〈Φ(γiJπ)|HDCB|Φ(γjJπ)〉 andH′ir=〈Φ(γiJπ)|H′|Φ(γrJπ)〉(i,j ∈M,r ∈N).By solving the generalized eigenvalue problem for the first-orderHeff,we can obtain the eigenvalues in the second-order approximation.

The Breit interaction,the higher-order retardation correction beyond the Breit interaction,and the leading QED corrections are also considered in the same way as for the MCDHF calculations.

2.3.Transition properties

Transition properties such as line strengthsS, weighted oscillator strengthsgf,and radiative ratesAfrom the stateγPJto the stateγ′P′J′are computed in perturbation theory in terms of reduced matrix elements

where the operatorT(EMK)depends on the multipolarity(E1,M1, E2, M2, etc.) of the transition.Inserting the CSF expansions for the wave functions, the reduced matrix element reduces to a sum over reduced matrix elements between CSFs.These matrix elements are finally obtained as sums over radial integrals using Racah algebra techniques.The above procedure assumes that the two statesγPJandγ′P′J′are built from the same set of orbitals.When this is not the case,e.g., when separate calculations have been done for the even and odd parity states, the representations of the wave functions are changed in such a way that the orbitals become biorthonormal,[35]in which case the calculation continues along the lines above.For electric transitions,the parameters can be computed in both length and velocity gauges,[36]where the results in the length gauge are preferred.

3.Results and discussion

3.1. K-,L-,and M-shells ions with Z ≤42

Using at least one of the three methods (RMBPT,MCDHF, and FAC-RCI), we carried out many theoretical studies of excitation energies and E1, M1, E2, M2 transition rates forK- andL-shell ions withZ ≤42, such as the ions in the sequences of H-like,[37,38]He-like,[39,40]Be-like,[41–45]B-like,[46–48]C-like,[49,50]N-like,[51–55]Olike,[56–60]F-like,[61–63]and Ne-like.[64]It is important to provide atomic data for more than just the levels of the lowest configurations in plasma modeling and diagnostics.To meet the demand for data,calculations of different ions in the He-,Be-,B-,C-,N-,O-,F-,and Ne-like sequences were provided from several dozen levels to several hundred levels,which are referred to as spectrum calculations.The range of ions,the targeted configurations and the number of studied states for each sequence are summarized in Table 1.

3.1.1.Excitation energies

The accuracy of all atomic structure calculations,including RMBPT and MCDHF,is determined by the way of comparing theoretical and experimental results, or by the way of comparing between accurate theoretical results of different calculations.Generally speaking,a trend for all atomic structure calculations, including RMBPT and MCDHF, is that the accuracy of excitation energies increases as the atomic numberZincreases and the effect of electron correlation diminishes along the isoelectronic sequence.

For example, in the study of O-like ions,[57]a comparison between the MCDHF and RMBPT excitation energies is carried out along the sequence withZ=24–30.Defining∆Ei ≡(EiRMBPT-EiMCDHF) for each of theNenergy levels that can be compared(i=1,...,N,andN=200),the average absolute difference between the two sets calculated from

with the standard deviation

In the study of F-like ions withZ= 24–30,[61]the same trend is found as the atomic numberZincreases along the isoelectronic sequence.The average relative differences(∆x±σ2)also decrease from 0.003%±0.016%for Cr XVI to 0.002%±0.007%for Zn XXII.

In Table 2 excitation energies in O-like Ni XXI from different calculations are compared with experimental values from the Atomic Spectra Database (ASD) of the National Institute of Standards and Technology (NIST).[65]Our MCDHF and RMBPT excitation energies are in good agreement, with the average absolute difference of∆E ±σ1=-481±511 cm-1.The previous theoretical energies from Refs.[66–68] depart from our MCDHF values with average difference of 1 379±14 851 cm-1, 29 279±15 742 cm-1,and 634±24 996 cm-1,respectively.Compared with the previous calculations, the average difference/uncertainty of the present MCDHF and RMBPT calculations go down by one or two orders of magnitude,and now,the calculated energies are accurate enough to detect misidentifications or errors in observational data,but also to serve as a valuable tool for identifying new lines.

Though many of the NIST excitation energies of Ni XXI show good agreement with our MCDHF and RMBPT values,the deviations from our values are larger than 10 000 cm-1for a few levels.For example, experimental energies from the NIST ASD are questionable for a fewn=3 states of Ni XXI.The values 8 035 000 cm-1for #12/2s22p3(4S)3s3S1,8 313 000 cm-1for #22/2s22p3(2P)3s3P1, 8 405 000 cm-1for #26/2s22p3(2P)3s3P2, and 8 422 000 cm-1for#26/2s22p3(2P)3s1P1do not have obvious counterparts in the present MCDHF and RMBPT calculations.Another 6 NIST values for the 2s22p33d levels,shown in Table 2,also deviate from our values by greater than 10 000 cm-1.

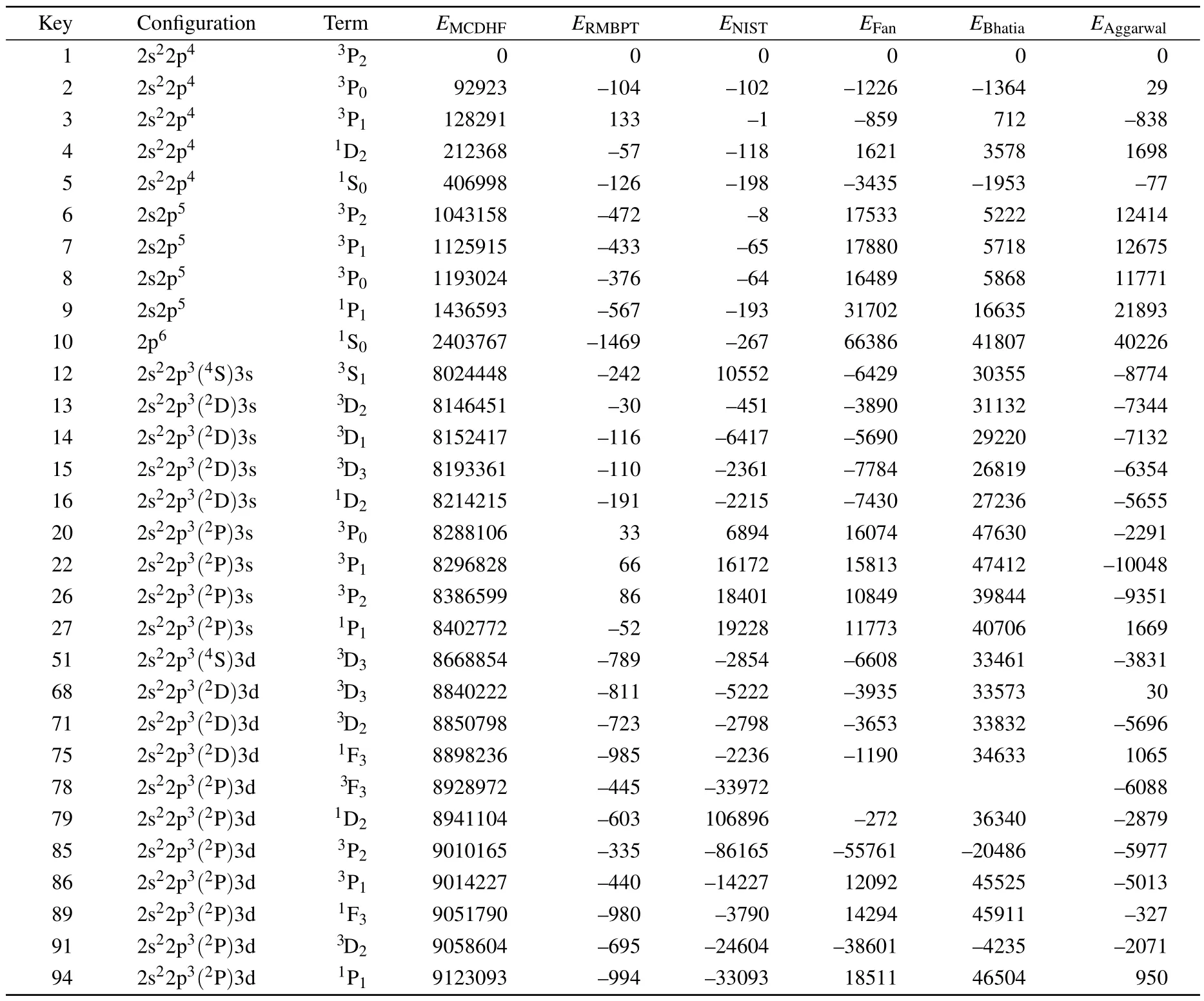
Table 2.Energy levels(in cm-1)relative to the ground state for the lowest 200 states of Ni XXI.For brevity,energies other than the present MCDHF values are listed as differences from the latter ones in cm-1. EMCDHF, ERMBPT – the present calculations; ENIST;[65] EFan:[66]EBhatia:[67] EAggarwal.[68] Our RMBPT and MCDHF results shown in this table are published in their entirety online.

For manyL-shell ions withZ ≤42, excitation energies for lower-lying states are known from observations.Going higher up comparatively less data are available, often associated with large uncertainties.The excellent description of energy separations of our calculations (MCDHF and/or RMBPT) along the isoelectronic sequence makes it possible to point out a number of lines for which experimental identifications are questionable.As an example, in Fig.1(a) we show the deviations of experimental values from the NIST ASD to our MCDHF excitation energies as a function ofZfor the 2s22p3(4S)3s3S1, 2s22p3(2P)3s1P1, 2s22p3(4S)3d3D3,and 2s22p3(2D)3d3D3levels of O-like ions.The deviations between the RMBPT and MCDHF excitation energies for the same levels along the sequence are shown in Fig.1(b).Good agreement is obtained between the present MCDHF and RMBPT values for the same levels along the sequence,and the differences between the two data sets(MCDHF and RMBPT)vary smoothly along the isoelectronic sequence.In comparison,a few of the NIST values depart from the MCDHF excitation energies by over 10 000 cm-1.Therefore,these experimental values compiled by the NIST ASD seem to be wrong or at least are affected by large errors.The situation is also well illustrated for the ions in the otherL-shell sequences of Belike,[41,42]B-like,[46,47]C-like,[49,50]N-like,[51]F-like,[61,62]and Ne-like.[64]

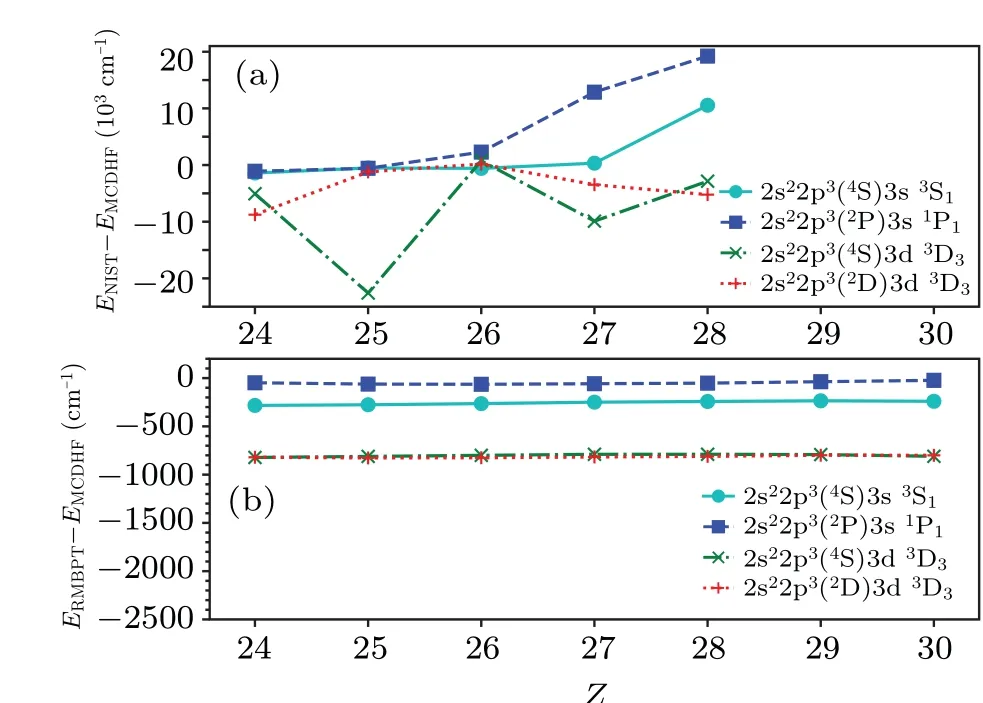
Fig.1.Energy deviations ((a) ENIST-EMCDHF and (b) ERMBPTEMCDHF) in cm-1 as a function of Z for the 2s22p3(4S)3s 3S1,2s22p3(2P)3s 1P1,2s22p3(4S)3d 3D3,and 2s22p3(2D)3d 3D3 levels of O-like ions.

TheM-shell ions withZ ≤30,especially the ions of iron group elements, produce strong extreme ultraviolet (EUV)spectral lines, which are routinely used to measure electron densities using data from,e.g.,the SOHO Coronal Diagnostic Spectrometer(CDS),see Ref.[69]and especially the Hinode EUV Imaging Spectrometer(EIS),see Refs.[70–74].The soft x-ray spectra are also rich inn=4→n=3 transitions fromM-shells ions of iron group elements.[75–77]Various current missions,such as Chandra with the Low Energy Transmission Grating (LETG), and the Solar Dynamic Observatory (SDO)with a suite of instruments,cover this wavelength range.[78,79]

Using the MCDHF method,we carried out many theoretical studies of excitation energies and E1,M1,E2,and M2 transition rates forM-shell ions withZ ≤32, such as the ions in the sequences of Si-like,[80]P-like,[81,82,85]S-like,[83]and Cllike.[84]The range of ions in different isoelectronic sequences,the targeted configurations, and the number of studied states for each ion of each sequence are summarized in Table 3.

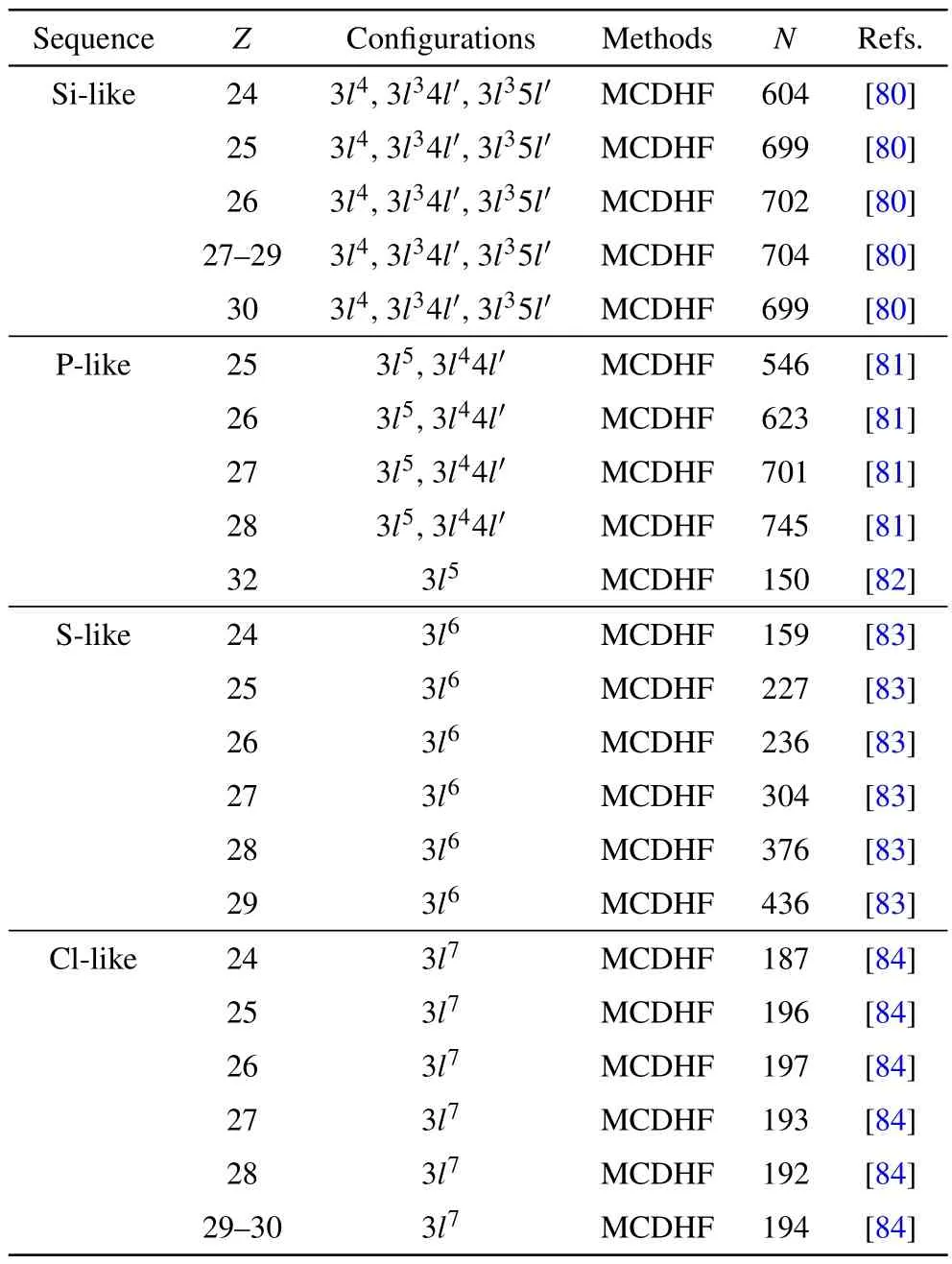
Table 3.Sequence,atomic number(Z)of ions,targeted configurations,and methods of the calculations,the number(N)of studied states for each ion.In the table l=0,...,n-1,and l′=0,...,n′-1.The excitation energies,E1,M1,E2,and M2 transition properties are studied for the targeted states in our previous works listed in the last column.

We reviewed the identifications of the transitionsn=4→3 andn=3→3 of Fe XIII, Fe XII, Fe XI, and Fe X, and some new identifications for these four ions were proposed.As an example,the identifications of the transitionsn=4→3 andn=3→3 of Fe XIII and Fe XII are shown in Table 4.Based on our MCDHF atomic data (wavelengths, radiative rates), and electron impact excitation rates provided by Del Zanna,[86,87]the relative intensities Int =NjAji/Ne(in photon units) are calculated using the collisional radiative model(CRM)[88]at a fixed temperatureTe[K]=106.3and at electron densities of 109cm-3(the first part)and 1013cm-3(the second part)relative to 3s3p33D◦1–3s3p2(3P)4s3P0(7–332)for Fe XIII, and 1019cm-3(the third part) for Fe XII relative to 3s23p3(43S)4S◦3/2–3s23p2(32P)3P4s4P5/2(1–292).The previous line identificationsn=4→3 andn=3→3 of Fe XIII and Fe XII in the EUV and x-ray wavelength range are reviewed by comprehensively comparing the MCDHF values with available experimental data.Discrepancies in the previous identifications for several cases,i.e.,12 cases in Fe XIII and 8 cases in Fe XII,have been found,and some tentative new(or revised)identifications(19 lines in Fe XIII and 5 lines in Fe XII)have been proposed.

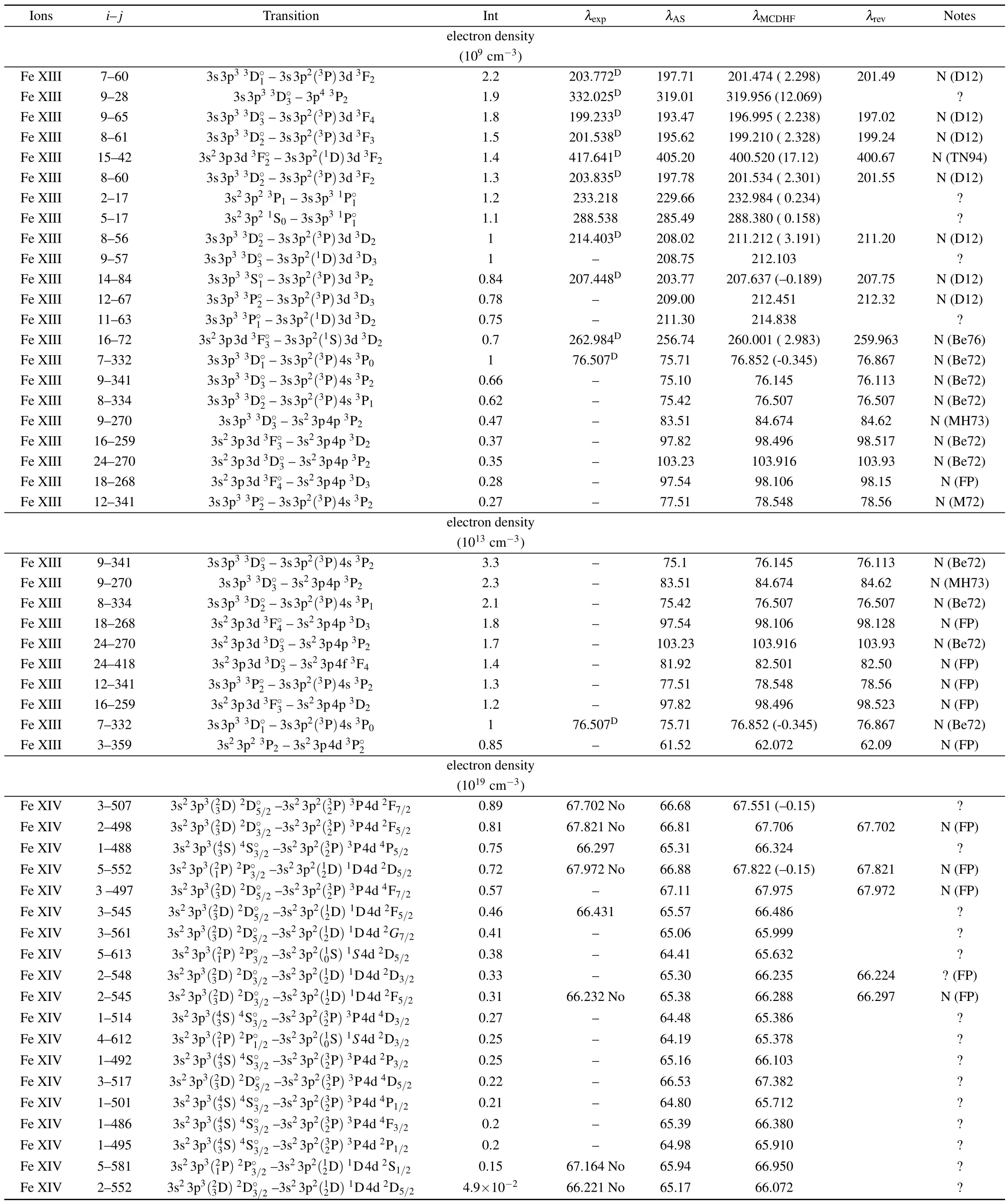
Table 4.A list of the strongest Fe XIII and Fe XII lines from the transition arrays n=3 →n=3 and n=4 →n=3.Using atomic data provided by Del Zanna,[86,87] the transitions are ordered by their relative intensities Int=NjAji/Ne (column 3, in photon units), calculated at electron densities of 109 cm-3(the first part)and 1013 cm-3 (the second part)relative to 3s3p33D◦1–3s3p2(3P)4s 3P0 (7–332)for Fe XIII,and 1019 cm-3 (the third part)for Fe XII relative to 3s2 3p3(43S) 4S◦3/2–3s2 3p2(32P) 3P4s 4P5/2(1–292).Column 4 gives the experimental wavelength λexp (˚A) from CHIANTI or NIST.We add a ’No’ if we consider the previous identification incorrect.Column 5 gives the AUTOSTRUCTURE (AS) wavelength λAS from Refs.[86,87].Column 6 is our present wavelength λMCDHF (with a difference with the experimental one in bracket), while the following column (λrev) reports any new experimental wavelength that we propose.The last column indicates if the identification of a line is questionable (?) or new (N).D indicates a new identification proposed by Del Zanna.[73,86] Be72,MH73,FP,M72,D12,Be76,TN94: wavelengths from Refs.[76,77,89–93].Some new wavelengths have been obtained from the spectra(the MH73 and FP spectra were reprocessed as described in Ref.[86]).More detailed information on Fe XIII and Fe XII line identifications can be found in our recent papers.[80,81]

3.1.2.Transition probabilities with uncertainty estimates

By comparing two sets of theoretical transition data obtained with two different methods (MCDHF and RMBPT),or by comparing the two sets of line strengths obtained using the lengthland velocity gaugesvfrom the MCDHF method,we used the uncertainty estimation method suggested by Kramida[94,95]to classify theoretical transition rates of the ions in different isoelectronic sequences listed in Tables 1 and 3,according to the NIST ASD[65]terminology(AA≤1%,A+≤2%,A≤3%,B+≤7%,B≤10%,C+≤18%,C≤25%,D+≤40%,D≤50%,and E>50%).

Fig.2.The relative difference δS =-F/max(,) of line strengths and for E1 transitions with BF≥10-5 among the lowest 702 levels of the n ≤5 configurations.

3.2.Highly charged tungsten ions

3.2.1. M-shell and N-shell tungsten ions

For the highly charged tungsten ions,our research group has already devoted to the study of the excitation energies,E1,M1, E2, M2, and E3 transition properties forM-shell (open 3p-and 3d-subshell)andN-shell(open 4p-subshell)tungsten ions[29,30,34,96–101]by using the RMBPT and MCDHF methods.The targeted configurations and the number of studied states for each tungsten ion are summarized in Table 5.We briefly review our previous works below.

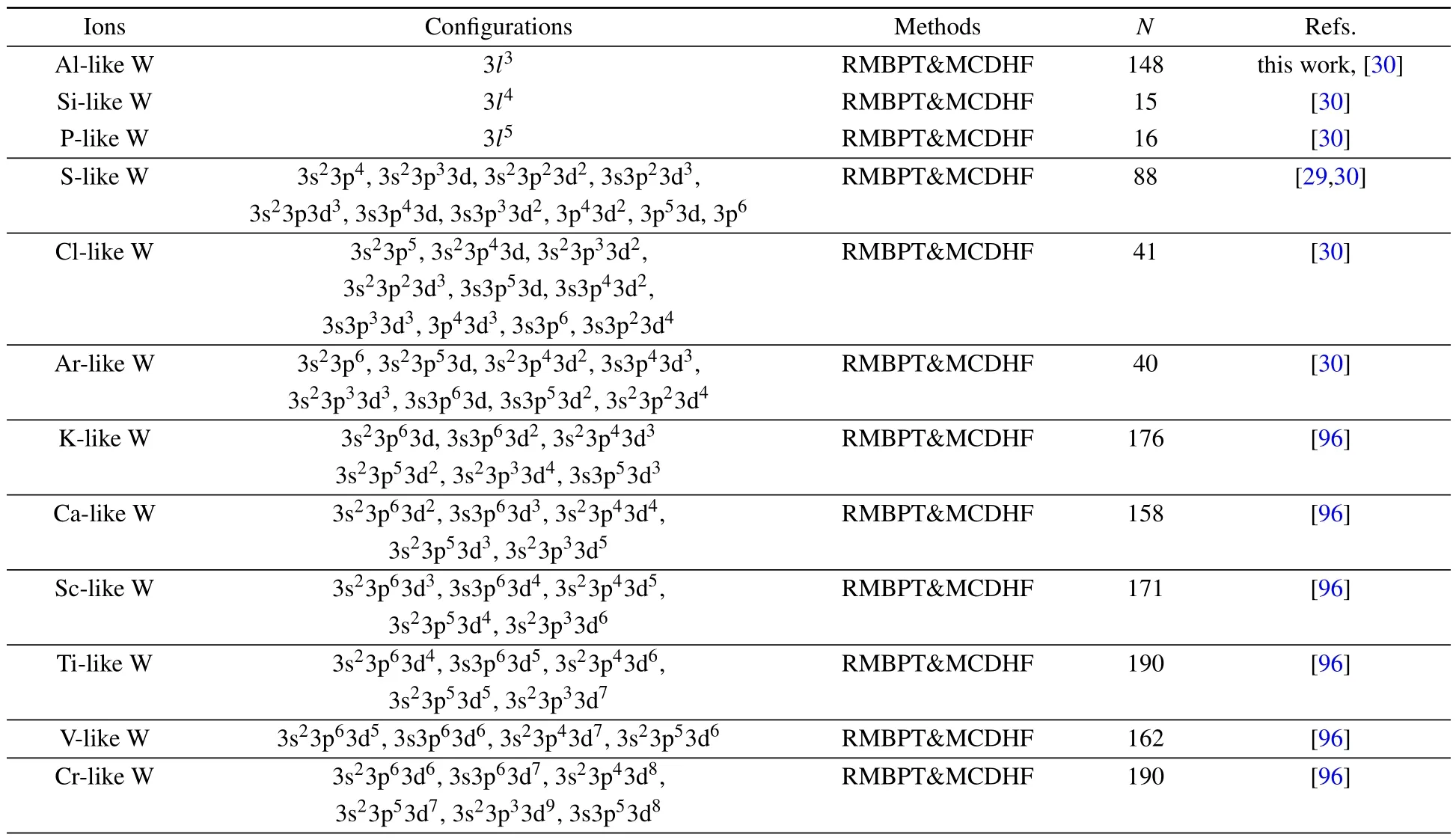
Table 5.Ions,targeted configurations,methods of the calculations,and the number(N)of studied states for each ion.In the table l=0,...,n-1.The excitation energies,E1,M1,E2,M2,and E3 transition properties are studied for the targeted states in our previous works listed in the last column.

Table 5.(Continued).

In our works forM-shell andN-shell tungsten ions,[29,30,34,96–101]atomic properties (ofn=3 states forMshell andn= 4 states forN-shell) including excitation energies, wavelengths, and transition properties from Al-like W61+through Co-like W47+, Ga-like W43+through Se-like W40+,and W38+ions are calculated and cross-checked by using the RMBPT and MCDHF approaches.The two datasets are in excellent agreement with each other on the order of 0.01% forM-shell and 0.1% forN-shell tungsten ions.Our theoretical results are in good agreement with experiments and show a clear improvement of accuracy over previous calculations.[5,6,102–113]And our calculations achieve spectroscopic accuracy to assist spectroscopists in their assignment and direct identification.Based on our RMBPT and MCDHF calculations and CRM simulations, we also give suggestions of assignments for all of the unidentified 28 spectral lines (a significant fraction, around sixty percent) of then=3→3 transitions measured by Lennartssonet al.[114]

Additionally,the contributions of electron correlation,the Breit interaction,the higher-order frequency-dependent retardation correction, and the leading QED corrections to excitation energies (transition wavelengths, and radiative rates) are also studied in detail.In the study for Al-like W61+through Co-like W47+ions,we point out that the Breit interaction and QED corrections(the corrections beyond the Dirac–Coulomb Hamiltonian), respectively, play an important role on the 3p–3d and 3s–3p excitation energies.The CV correlation involving the 2p and 2s core electrons and the higher-order retardation corrections beyond the Breit interaction should also not be ignored for getting results with spectroscopic accuracy.In the study for Ga-like W43+through Kr-like W38+ions, we also find that the CV correlation of 3d and 3p is important for reaching close to spectroscopic accuracy for the transition energies.

Especially, we investigate in detail the three different methods to estimate the SE corrections.The first one is that SE corrections are obtained based on a screened hydrogenic approximation in the current GRASP2K package[22](usually called GRASP2K).The second one is a screening approximation based on the Welton interpretation[115]and implemented in GRASP2K by Loweet al.,[116]starting from the latest available hydrogenic values[117,118]modified to account for finite-nuclear-size effects[119,120](usually called Welton).The last one is a model QED operator,which also includes the non-local QED part to evaluate the SE corrections for manyelectron atomic systems, has been developed by Shabaevet al.[31,32](usually called ModelQED).Based on our systematic assessment,[29,30,34]the Welton and ModelQED methods are more recommended to estimate the SE potential for highlycharged tungsten ions than the GRASP2K method.

3.2.2.Excitation energies for Al-like W61+

In the present MCDHF calculations,the QED corrections are estimated using the three different models,i.e.,GRASP2K,Welton, and ModelQED (see Refs.[29,30] for details).And the corresponding MCDHF results(labelled GRASP2K,Welton,and ModelQED,respectively)are compared with the experimental values[121,122]in Table 6.The corresponding differences ∆ETheo.=ETheo.-EExpt.(in cm-1)are listed as well.From Table 6,it is found that the Welton and ModelQED excitation energies are in general within or close to the experimental estimated uncertainties, with average differences±standard deviations of-672±1441 cm-1(-0.018%±0.043%)and-331±1594 cm-1(-0.006%±0.052%), respectively,for the 7 levels listed in Table 6.However, the GRASP2K excitation energies differ from the experimental values by-1468±1208 cm-1(-0.052%±0.050%).As observed in our recent works,[29,30]the values from the Welton and ModelQED calculations are generally closer to the experimental values than the values from the GRASP2K calculation.In the following, the MCDHF results will be all based on the ModelQED model which turns out to be the best model for describing the self-energy QED correction.

Table 6.Excitation energies(E,in cm-1)from the present MCDHF calculations compared with the experimental values(expt).[121,122] The estimated uncertainty of the experimental value for each level is reported in brackets in the Expt column.In the present MCDHF calculations,the QED corrections are estimated by using the three different models,i.e.,GRASP2K,Welton,and ModelQED(see Refs.[29,30]for details).The corresponding differences∆ETheo.=ETheo.-EExpt. (in cm-1)are also listed.

In our previous work for tungsten ions with an open 3psubshell,[30]only excitation energies and wavelengths for a few levels are provided.As a complement, the complete results incorporating excitation energies, E1, M1, E2, and M2 transition properties,and level lifetimes for the lowest 148 levels belonging to the 3l3configurations for Al-like W61+from the RMBPT and MCDHF calculations are presented in this work.The details of the calculations have already been explained in Ref.[30]and do not repeat here.

We also ought to resume the previous relevant theoretical studies.Using the older GRASP package(GRASP89)[124]and the FAC,[26]Aggarwal and Keenan[103]calculated excitation energies, radiative rates, and lifetimes for W61+.Also using the GRASP89 code,[123]Xuet al.[104]studied excitation energies, wavelengths and transition probabilities for W61+.The excitation energies and wavelengths for only a fewn=3 levels of W61+were provided by Chen and Cheng[106]using the RCI method.Ekmanet al.[124]also calculated excitation energies and transition probabilities for W61+using the RMBPT and MCDHF methods.

For comparison, the present RMBPT and MCDHF excitation energies for Al-like W61+as well as the compiled data from the NIST ASD[125]are listed in Table 7.The two theoretical data sets (GRASP89 and FAC) reported by Aggarwal and Keenan,[104]the theoretical results provided by Xuet al.(MCDHF2),[106]and the values(RCI)calculated by Chen and Cheng[107]are also included in Table 7.

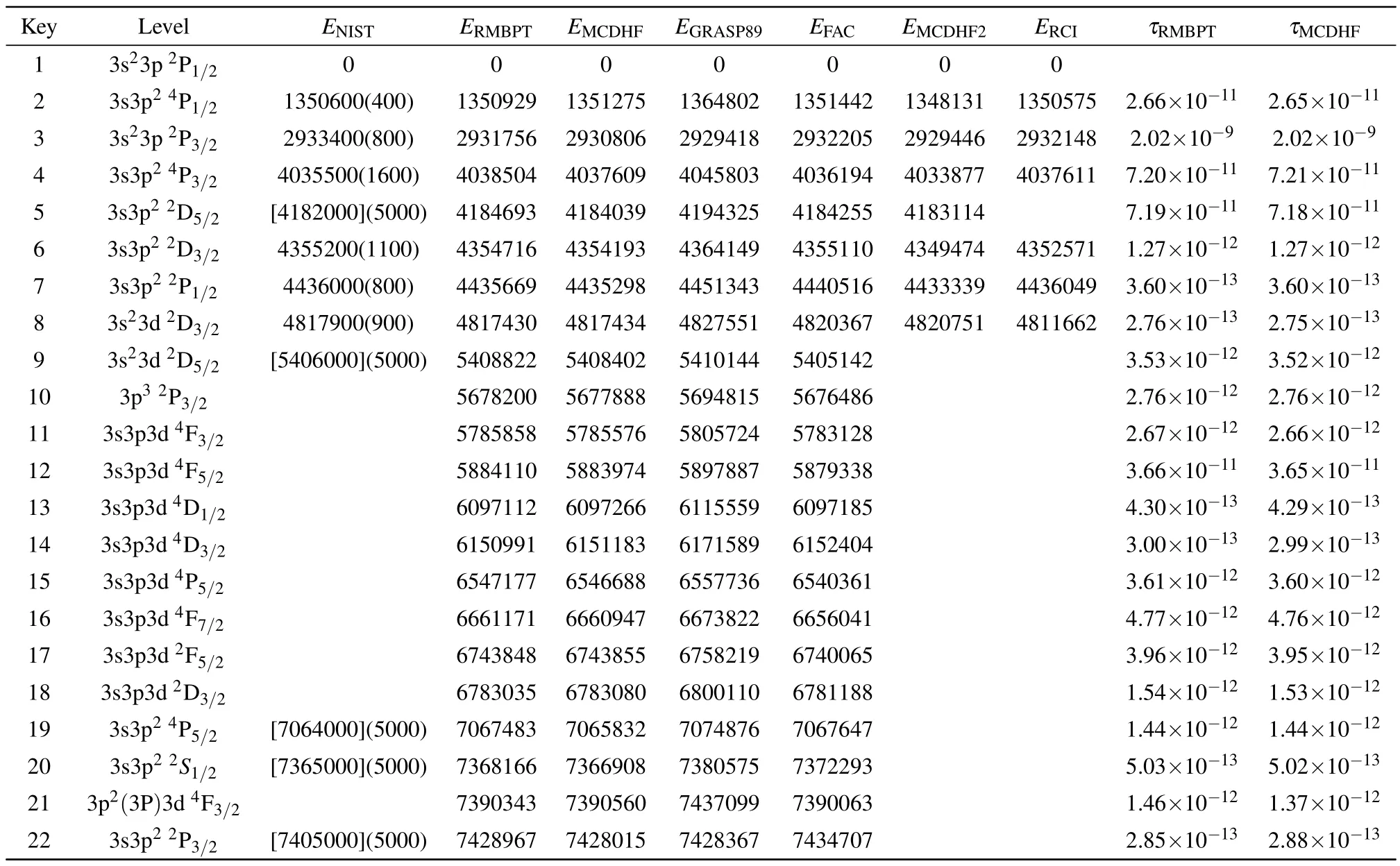
Table 7.Comparison of the excitation energies (E, in cm-1) from the present RMBPT and MCDHF, from the previous works (GRASP89 and FAC:from Aggarwal and Keenan;[103] MCDHF2: from Xu et al.;[104] RCI: from Chen and Cheng[106]), and from the measurements.[121,122] The NIST compiled values reported in square brackets are determined by semi-empirical parametric calculations using Cowan’s code.The rest of the NIST values are deduced from measured lines.The number reported in parenthesis, after the experimental wavelength, is the estimated experimental uncertainty.The present RMBPT and MCDHF level lifetimes(τ,in s-1)are also listed.The excitation energies and lifetimes from the present RMBPT and MCDHF calculations shown in this table are published in their entirety online.

The NIST compiled values in square brackets are determined from semi-empirical calculations by Kramida[126]using Cowan’s code.[127]The other NIST values are deduced from measured lines that were observed using the EBIT facilities.[121,122]For each level,the number reported in parenthesis,after the NIST excitation level energy,is the estimated accuracy provided by the NIST ASD.It can be seen from Table 7 that the uncertainty of the NIST values quoted in square brackets is 5000 cm-1, whereas the NIST values deduced by measured lines are much more accurate(400 cm-1–1600 cm-1).

The energy differences, ∆E=EOthers-ERMBPT, of the different theoretical excitation energies and the NIST compiled values from the present RMBPT results are shown in Fig.3.The present MCDHF and RMBPT are in good agreement with each other,with an average difference with the standard deviation of-370 cm-1±518 cm-1(-0.007%±0.01%)for the lowest 22 levels listed in Table 7.The present RMBPT and MCDHF results agree with the NIST compiled experimental values within 3000 cm-1(0.07%) and 2600 cm-1(0.09%), respectively, which are generally within or closed to the NIST estimated uncertainties.However,the GRASP89 results of Aggarwal and Keenan[103]deviate from the NIST compiled experimental values by up to≃14000 cm-1(100%)and not less than≃-4000 cm-1(0.1%).On the contrary,their FAC results agree more with the NIST compiled measured values than the GRASP89 results, with the differences by up to 4500 cm-1(0.1%).Similarly, the excitation energies calculated by Xuet al.[104]and Chen and Cheng[106]are lower than the NIST compiled measured values by up to≃5700 cm-1(0.1%)and 6200 cm-1(0.1%),respectively.

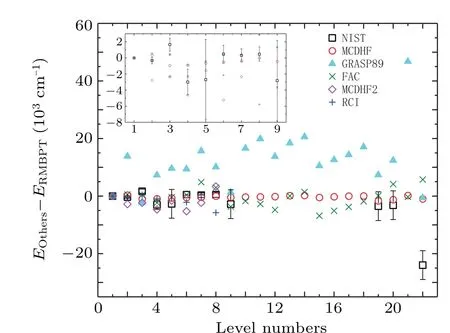
Fig.3.The deviations for the excitation energies in Al-like W61+between the different theoretical (the present RMBPT and MCDHF,as well as the previous works: GRASP89 and FAC: from Aggarwal and Keenan;[103] MCDHF2: from Xu et al.;[104] RCI: from Chen and Cheng[106]),and experimental values.[121,122]Vertical error bars are experimental uncertainties.The inset shows the enlargement of differences for the lowest 9 levels.

The differences between the previous calculations of excitation energies[103,104,106]and the measured values compiled in NIST are several times or more than one order of magnitude larger than the corresponding differences calculated for the present RMBPT and MCDHF results.This indicates that the present theoretical excitation energies of Al-like W61+are highly accurate and represent a great improvement on the latest theoretical results.[103,104,106]

Looking at the NIST values that are reported in square brackets to mark their origin from semi-empirical parametric calculations,their differences with the present theoretical values are up to 24000 cm-1.For this reason, our RMBPT and MCDHF excitation energies,compared with these NIST compiled values, also represent a substantial improvement in accuracy.As already mentioned in our recent work for S-like W58+,[29]we, therefore, recommend the use of our theoretical values (not only for W61+and W58+, but also for other highly-charged tungsten ions) for updating these NIST semiempirical data, and even suggest their use as input data for a new parametric fit using Cowan’s code,which would increase dramatically the accuracy and quality of the NIST compiled values.

The excitation energies of the lowest 148 levels from the present RMBPT and MCDHF are published in their entirety online.Our two datasets can cross-check with each other,and the average difference with the standard deviation between them for the lowest 148 levels is found to be-661 cm-1±513 cm-1(-0.006%±0.006%).

3.2.3.Transition properties for Al-like W61+

In Table 8, wavelengths (λ, in ˚A), transition rates (A,in s-1), line strengths (S, in a.u.), and weighted oscillator strength (gf, dimensionless) obtained from the present RMBPT and MCDHF calculations for the E1, E2, M1, and M2 transitions among the lowest 148 levels, with radiative branching ratios (BRs) over 0.1% for Al-like W61+, are presented.The last column represents the estimated accuracy of theS-values using the terminologies of the NIST ASD.[125]Our transition properties are given in the Babushkin gauge.

There are in total 3270 transitions originating from Allike W61+with BRs over 0.1% in Table 8.These transitions lie in a wide wavelength range from 7 ˚A to 230 ˚A, and all of them are in x-ray and EUV ranges.The average difference with the standard deviation between our two data sets for these 3270 transitions is found to be-0.0003%±0.03% for wavelengths,-2%±13%for transition rates,-2%±13%for weighted oscillator strength,and-0.0002%±0.001%for line strengths.

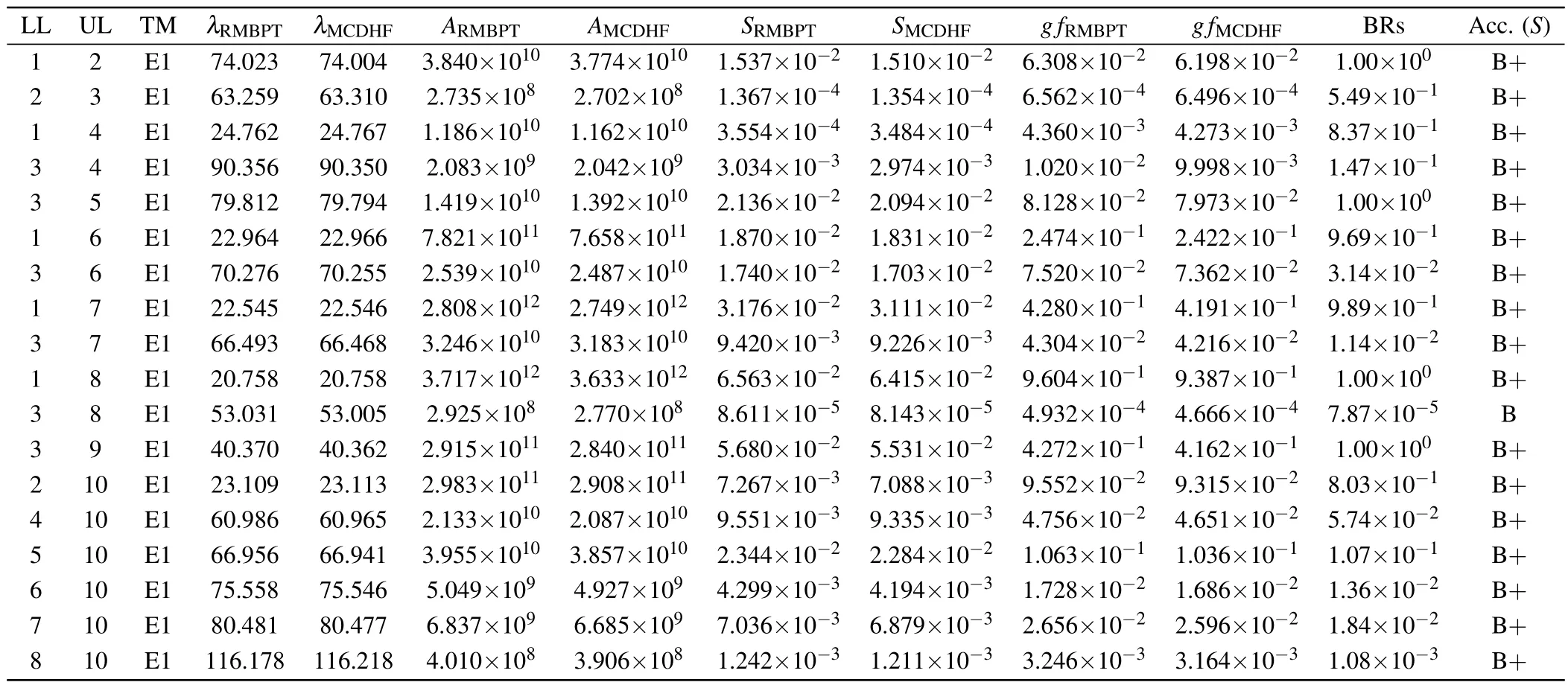
Table 8.The present RMBPT and MCDHF wavelengths(λ,in ˚A),transition rates(A,in s-1),line strength(S,in a.u.),and weighted oscillator strength(g f, dimensionless), with radiative branching ratios (BRs) over 0.1% for Al-like W61+.The last column represents the estimated accuracies of the S-values using the terminologies of the NIST ASD.[125] This table is available in its entirety online.Some selected transitions are shown here for guidance regarding their form and content.

Figures 4 and 5 respectively show the differences between the present RMBPT and MCDHF wavelengths and transition rates for all of the transitions listed in Table 8.As we can see,84%of our two datasets for transition wavelengths agree with each other within 0.03%,and 84%of our two datasets for transition rates agree with each other within 10%.

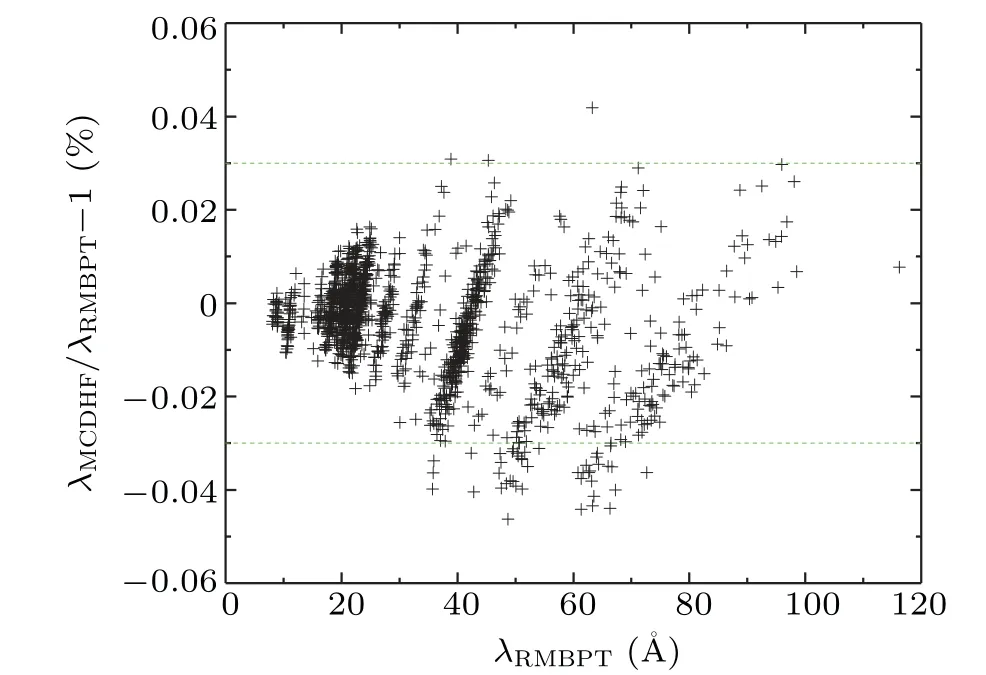
Fig.4.The deviations between the present RMBPT and MCDHF transition wavelengths for Al-like W61+.

Furthermore, the uncertainty estimation method, proposed by Kramida,[94,95]is used to classify the accuracy of the present RMBPT and MCDHFS-values, according to the NIST ASD[125]terminology(AA≤1%,A+≤2%,A≤3%,B+≤7%, B≤10%, C+≤18%, C≤25%, D+≤40%, D≤50%,andE>50%).The estimation details can be seen in our recent works.[63,96]For the 2673 E1 transitions originating from W61+listed in Table 8, about 55.2% have uncertainties 3%≤δ ≤7% (B+), 15.8% withδ ≤10% (B), 13.2% withδ ≤18%(C+),9.6%withδ ≤25%(C),and only 6.2%withδ ≥25% (D, D+, and E).It should be noted that the uncertainty of theS-value of each transition is estimated by including all transitions of each ion considered,without any restriction on the line intensity values in the uncertainty estimation procedure, although only transitions with BRs over 0.1% are provided in Table 8.The uncertainties of the present RMBPT and MCDHFS-values of E2,M1,and M2 transitions are also estimated as for the E1 ones.

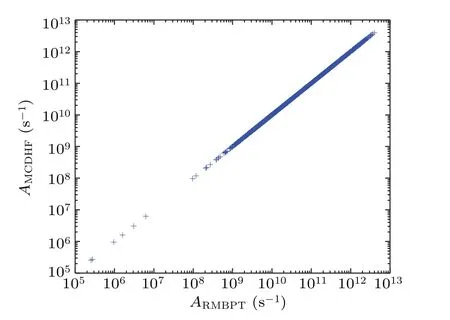
Fig.5.The comparison of the present RMBPT and MCDHF transition rates for Al-like W61+.

3.2.4.Level lifetimes for Al-like W61+

In Table 7, the present RMBPT and MCDHF level lifetimes for the lowest 22 levels in Al-like W61+are listed, and the complete datasets for the lowest 148 levels are also published in their entirety online.Figure 6 shows the differences between the present RMBPT and MCDHF level lifetimes for the lowest 148 levels in Al-like W61+.One can see that our two data sets are in good agreement with each other,and most of the differences between them are within 0.3%,even though the present MCDHF level lifetimes are generally lower than RMBPT ones.

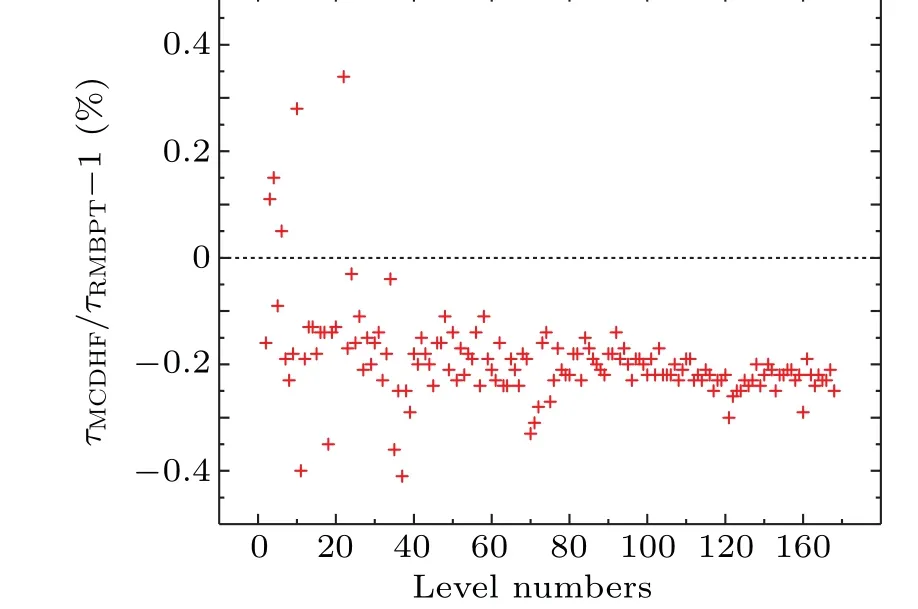
Fig.6.The comparison of the present RMBPT and MCDHF level lifetimes for Al-like W61+.

4.Conclusions and outlook

Employing two different and independent methods, i.e.,MCDHF and RMBPT, we have systematically studied the atomic radiative data such as excitation energies, transition wavelengths, radiative rates, and level lifetimes for the ions withZ ≤42 and tungsten (Z=74) ions to meet demands of astrophysical and fusion plasmas.In this work,we mainly review our previous works performed in the past decade.As a complement/extension to our previous works for highly charged tungsten ions with openM-shell and openN-shell,we also present and discuss our complete RMBPT and MCDHF calculations for the excitation energies,wavelengths,E1,M1,E2, and M2 transition properties, and level lifetimes for the lowest 148 levels belonging to the 3l3configurations in Al-like W61+.And the calculations forL-shell,N-shell, and lowercharged tungsten ions will be reported in future works.

By cross-checking two datasets from our RMBPT and MCDHF calculations and comparing them with other theoretical calculations and available experiments in the literature,we summarize the uncertainties of our systematical calculations here.ForK- andL- shells ions withZ ≤42 the uncertainty of calculated transition wavelengths is about 0.01%–0.05%.For theM-shell ions withZ ≤42, the uncertainty of calculated transition wavelengths is on the order of 0.1%.For theM-shell tungsten ions,the uncertainty of calculatedn=3→3 transition wavelengths is about 0.01%–0.05%.And for theNshell tungsten ions, the uncertainty of calculatedn=4→4 transition wavelengths is on the order of 0.1%.

We expect that our theoretical calculations with high precision provide precise benchmarks for other theoretical calculations and experimental measurements as well as applications for abundance analysis, simulation, and diagnostics in astrophysical and fusion plasmas.

Additionally, in our recent works[128,129]we mainly focused on discussing in detail how to improve the efficiency of the RSCF procedure of the MCDHF method and the RCI calculations.For the RSCF, the routines for calculating the direct and exchange potentials and the Lagrange multipliers are redesigned.[128]For the RCI, regrouping CSFs and introducing CSF generators allow for a substantial reduction of the computational load.[129]Compared with the original GRASP codes, our contributions reduce CPU times by a few tens or more factors.A large amount of atomic data of high accuracy for more complex ions is expected to be provided in the future.

Data availability statement

The data that support the findings of this study are openly available in Science Data Bank at https://doi.org/10.57760/sciencedb.10569.

Acknowledgements

We acknowledge the support from the National Natural Science Foundation of China (Grant Nos.12074081 and 12104095).Many works reviewed here are accomplished in close collaboration with other groups,such as members of the CompAS group,and M.F.Gu(author of the FAC code),etc.