Fast and perfect state transfer in superconducting circuit with tunable coupler

Chi Zhang(张驰), Tian-Le Wang(王天乐), Ze-An Zhao(赵泽安), Xiao-Yan Yang(杨小燕),Liang-Liang Guo(郭亮亮), Zhi-Long Jia(贾志龙), Peng Duan(段鹏), and Guo-Ping Guo(郭国平),3,‡

1CAS Key Laboratory of Quantum Information,University of Science and Technology of China,Hefei 230026,China

2CAS Center for Excellence and Synergetic Innovation Center in Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China

3Origin Quantum Computing Company Limited,Hefei 230026,China

Keywords: quantum state transfer,superconducting circuit,tunable coupler

1.Introduction

Quantum computing has long held the promise of solving intractable problems that its classical counterpart cannot.[1,2]Superconducting quantum circuit is one of the leading candidates to build a practical quantum computer,[3]on which the experimental quantum advantage is firstly demonstrated.[4,5]Transferring information from one location to another is a fundamental requirement for both classical and quantum information processing.[6–9]High-fidelity quantum state transfer is crucial for realizing a large-scale quantum computer[10]and harnessing the full potential of contemporary state-of-the-art quantum processors.[11–14]Longdistance quantum information transfer is necessary for the communication between quantum processors,which is usually accomplished through photon-mediated[7,15,16]or phononmediated[17]quantum state transfer with the additional interface between stationary qubits and flying qubits.As to shortdistance quantum state transfer, a key ingredient in on-chip quantum information processing, various theories have been proposed for high fidelity quantum state transfer(QST)across a stationary lattice.[8,9,18,19]

Specifically, the perfect state transfer protocol[18](PST)realizes perfect QST across a stationary coupled lattice through Hamiltonian evolution for a fixed period of time.In anNsite linear chain, the state of sitencan be transferred to siteN-n+1 perfectly with pre-engineered inter-qubit interaction.So far,PST has been experimentally demonstrated in nuclear magnetic resonance systems,[20]in optical systems with an array of coupled waveguides,[21]and in solid-state quantum systems with a chain of four superconducting transmon qubits in the fixed coupling architecture.[22]The experiment performed in the superconducting circuit relied on full control of the effective couplings between neighboring qubits by parametrically modulating the qubits.In this approach, the tunable range of the effective coupling strength is considerably limited by the intrinsic geometric coupling of the circuit,which limits its transfer speed.Moreover, due to the alwayson coupling, the send-qubit and the receive-qubit can not be isolated from the chain before and after the transfer process;this will degrade its performance in a quantum network.To overcome these drawbacks, tunable coupler would be desirable in the transfer channel,[10,17]see Fig.1(a).Recently,the tunable coupler architecture proposed by Yan Feiet al.[23]and its variants[24,25]have been wildly used in large-scale superconducting quantum processors.The tunable coupler is almost the same as a tunable qubit,which makes it highly compatible with state-of-the-art control and fabrication methods of superconducting circuits.The coupling strength can be tuned over approximately three orders of magnitude,and the residualZZinteraction between neighboring qubits can also be effectively suppressed,[26]which is favorable for simultaneous quantum operations.

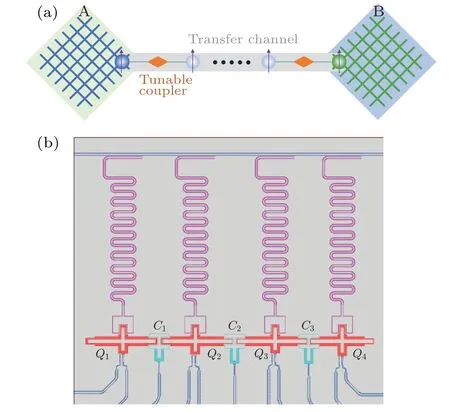
Fig.1.(a)Two sub-processors A and B are connected with a PST channel.The tunable couplers in the transfer channel can be turned on to allow information flow between A and B, and can also be turned off to ensure independent functioning of the two sub-processors.(b) The layout of our device.Our sample is a four-qubit chain (red, Q1–Q4)and each nearest-neighbor two qubits are coupled via a coupler (blue,C1–C3).All the qubits and couplers are frequency tunable transmons.

In this work, we utilize this tunable coupler architecture to demonstrate a fast and high-fidelity PST in a chain of four superconducting transmon qubits with tunable couplers in between.With the high on–off ratio of the tunable couplers,the transfer cycle is accomplished efficiently in a single step,and it is as fast as 25 ns, comparable to the shortest duration of a single swap operation in superconducting circuit.[26,27]To realize the exact Hamiltonian required for PST, we employ the differential evolution(DE)algorithm[28]to fine-tune the control parameters and realize nearly PST with a fidelity of 0.986.Simulation and a more detailed error matrix analysis show that this fidelity is mainly limited by the short decoherence time of our sample.

2.Experiment setup and methods

Our experimental device is depicted in Fig.1(b), where four frequency-tunable transmon qubits(Q1–Q4)line up with the tunable couplers (C1–C3) sandwiched between each pair of qubits.Each qubit,dispersively coupled to an independent readout resonator,has its ownXYandZcontrol lines;the coupler is only equipped withZcontrol line.The frequency of the qubit or coupler can be tuned dynamically using ac-bias or statically using dc-bias applied on itsZcontrol line.The effective coupling strength between a pair of adjacent qubitsQiandQi+1can be described by[23]

Now the only control parameters aregi.Furthermore, according to Eq.(1),giis solely determined by the frequency ofCi.According to the theory reported in Ref.[18], a quantum state can be transferred perfectly over a qubit chain of any length as long as one can pre-engineer inter-qubit interactions.In addition, in a linear chain ofNqubits, PST requires the coupling strengths to follow the functionwhereg0is a constant.In this condition, when we prepareQiin state|ψi〉=α|g〉+β|e〉, and all other qubits are in the ground state|g〉(|e〉represents the excited state),after a durationτ=π/2g0,QN-i+1will be in the state|ψN-i+1〉=|ψi〉(up to a phase factor), and meanwhile all other qubits would turn back to|g〉.That is,the state from siteican be perfectly transferred to siteN-i+1.

Before showing the tunability of thegi, we note that the frequency of each qubit is also dependent on the frequency of the nearest-neighboring coupler owing to the strong coupling between them;[29]this will make the tuning process complicated.However,this dependence can be released by compensating the qubit frequency when tuning its adjacent coupler with a pre-calibration experiment.As shown in Fig.2(a), we fix the drive frequency ofQ4at the working point while scanning the qubitZbias and the nearest-neighboringC3Zbias simultaneously.The fitted red dashed line in Fig.2(a)indicates the compensatedZbias ofQ4for eachZbias ofC3aroundQ′4working point.With this calibration data, the compensation can be done automatically in software, enabling the independent control of qubit frequency and coupler frequency.

The effective inter-qubit coupling strengthgican be extracted from the swap spectroscopy betweenQiandQi+1.To demonstrate its tunability, takingg3for example, we prepare|0010〉 by applying aπpulse toQ3at its idle point.Then we apply a rapidZpulse onQ3so that|0010〉and|0001〉are on resonance and meanwhile turning onQ3–Q4coupling by adjusting theZbias amplitude ofC3.We wait for a variable delay timeτand measure the state population transferred to|0001〉as a function ofτandZbias ofC3.By fitting the oscillation frequencies in Fig.2(b), we plot the effective coupling strengthg3as a function ofZbias ofC3,as shown in Fig.2(c).The inter-qubit coupling strength can be turned off and on to more than 30 MHz.In the same way, we determineg1andg2as a function of theZbias of the corresponding coupler,respectively.

Figure 3(a)shows the pulse sequences for the state transfer process.We prepareQ4in the excited state while all other qubits stay in the ground state and bring all the qubits and couplers into their working point where the qubits are on resonance andg1:g2:g3=Then we measure the population of each qubit simultaneously as a function of pulse lengthτ.Flat-top Gaussian pulses are used to suppress the unwanted leakage onto non-computational states.The pulse amplitudes are obtained iteratively using the calibration procedures shown in Figs.2(a) and 2(b).To further optimize these amplitudes, we use the DE algorithm to minimize the mean squared error between the numerically simulated and experimentally measured trajectories.The final result is shown in Fig.3(b) forg2/(2π)=20 MHz, where the population ofQ4(red circle) flows toQ3,Q2andQ1(blue circle) in turn.The full lines correspond to numerical simulation results.The population ofQ4is completely transferred toQ1att=25 ns,as expected.Besides, the evolution of population indicates that the transfer continues to go forward and backward astincreases.Att=50 ns,the population ofQ1is transferred back toQ4in turn.As shown below,these repeated transfer cycles offer a straightforward method to benchmark the performance of the process fidelity of QST,[22]such that errors inevitable during state preparation and measurement(SPAM)can be ignored.

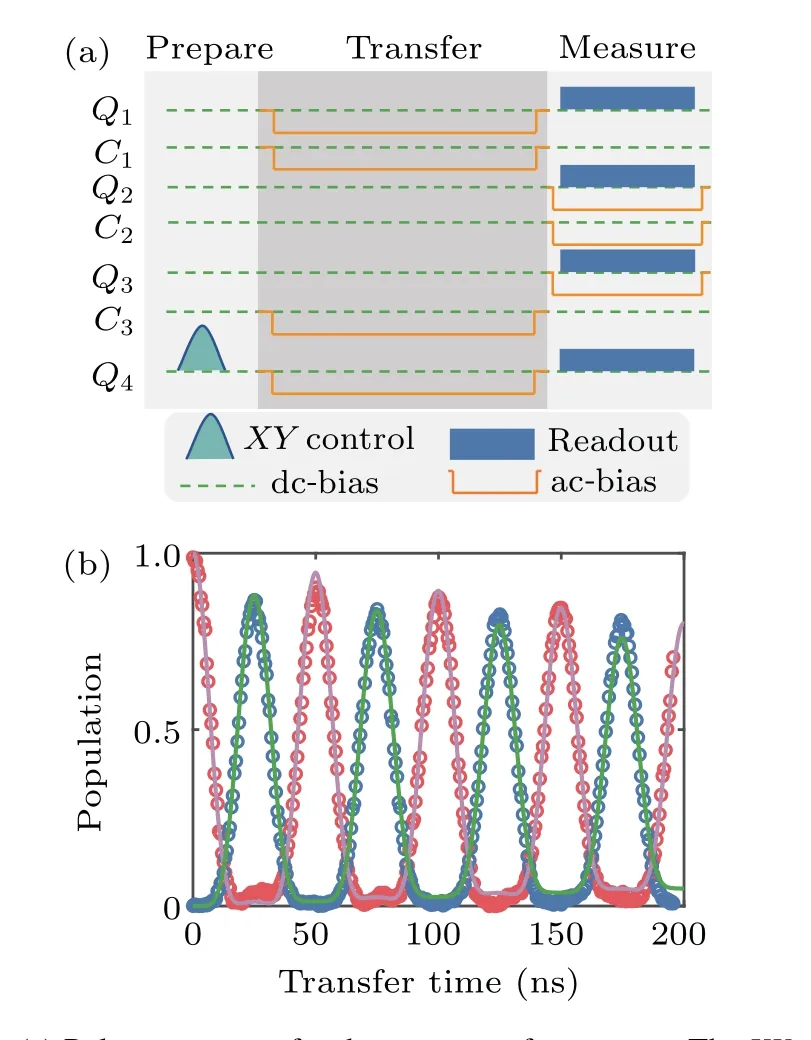
Fig.3.(a)Pulse sequences for the state transfer process.The XY control pulse is only applied on Q4 to prepare arbitrary single qubit state.The ac-bias is applied on Q1, Q4,C1,C3 during the transfer period to bring them to working point, and is also applied on Q2, Q3,C2 during the simultaneous measurement duration.(b)Experimentally measured(circle) and numerically simulated (line) dynamic population flows of Q4 (red)and Q1 (blue)during the transfer process.

3.Results

Fig.4.PST process fidelity.(a) Process fidelity Fp decays as transfer number m grows.The error bars are obtained from five repeated experiments representing one standard deviation.Fitting the fidelity data to F = APm+B (orange solid line), we get P = 0.986, representing a high fidelity QST.(b) Process matrix without SPAM errors for m=2 in the basis of Pauli matrices, with a fidelity Fp(m=2)=0.965,from which we estimate the fidelity of single QST Fp(m=1)==0.982,agrees well with the ftiting result in(a).(c)The diagonalized matrix Λ of χerrnoSPAM for m=2,whose largest eigenvalue ΛII is related to the decoherence error, εdec = 1-ΛII =3.06%.The height and color of the bars correspond to the amplitude and phase of the matrix elements,respectively.The transparent outline shows the ideal value.

4.Conclusion

In conclusion, we experimentally realized a fast (25 ns)and high-fidelity(0.986)PST in a chain of four superconducting transmon qubits with tunable coupler architecture.This efficient state transfer is made possible by the large on–off ratio of the tunable coupler.Currently,decoherence is the main error source in PST process.We anticipate that better coherence will further improve PST performance.The PST demonstrated in this work constitutes an important tool for on-chip entanglement generation and distribution.Our technique can also be directly generalized to other different configurations to allow more robust QST,[33–35]and extend to a larger chain or multi-node quantum network,[36]making it a valuable tool for scalable quantum information processing.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.12034018 and 11625419).This work is partially carried out at the USTC Center for Micro and Nanoscale Research and Fabrication.