Analytical wave solutions of an electronically and biologically important model via two efficient schemes
2023-12-02QingboHuangAsimZafarRaheelandAhmetBekir
Qingbo Huang, Asim Zafar, M.Raheel, and Ahmet Bekir
1Chongqing College of Architecture and Technology,Chongqing 401331,China
2Department of Mathematics,COMSATS University Islamabad,Vehari Campus,Pakistan
3Neighbourhood of Akcaglan,Imarli Street,No.28/4,Eskisehir 26030,Turkey
Keywords: spacetime fractional Fitzhugh–Nagumo model, truncated M-fractional derivative, expa function scheme,EShGEE scheme,analytical wave solutions
1.Introduction
Different types of phenomena occurring chemically,biologically, economically and others come from nonlinear partial differential equations (NLPDEs).Many different methods have been developed to gain analytical wave solutions of these NLPDEs, i.e., optical soliton solutions of coupled nonlinear Schr¨odinger equations have been gained with use of KudryashovR-function technique,[1]some new kinds of optical soliton solutions of time-fractional perturbed nonlinear Schr¨odinger equations have been achieved by using the generalized Kudryashov scheme,[2]by applying the modified auxiliary equation technique, optical wave solutions of timefractional resonant nonlinear Schr¨odinger equations have been obtained,[3]new optical wave solutions for the time-fractional perturbed nonlinear Schr¨odinger equations have been achieved by utilizing the improved tan[φ(ζ/2)]-expansion scheme,[4]different kinds of optical wave solitons of time-fractional paraxial wave equations have been gained by using the Sardar sub-equation method,[5]various optical wave solutions of three-component coupled nonlinear Schr¨odinger equations have been attained with the help of generalized exponential rational function scheme,[6]dark, bright, singular and periodic solitary wave solutions of generalized fractional Davey–Stewartson equations have been obtained by applying the generalized projective Riccati equation technique,[7]some exact wave solutions of the Lax equation have been achieved by applying the extended sinh-Gordon expansion technique,[8]kink solitons of the Sharma–Tasso–Olver–Burgers equation have been attained by using Kudryashov and exponential techniques,[9]traveling wave solutions of perturbed Biswas–Milovic equations have been gained with the use of improvedF-expansion technique,[10]some new optical wave solutions of complex Korteweg–de Vries equations have been obtained by applying the unified scheme.[11]Similarly, Hirota bilinear method,[12]modified extended tanh expansion method,[13]modified simplest equation technique,[14]extended Jacobi elliptic function scheme,[15]sech and tanh function solutions are obtained by using the sine-Gordon expansion scheme,[16]sinh,cosh, sin and cos involving solutions are gained by utilizing the rational sine-Gordon expansion technique[17]and many other techniques.[18–24]
In this study, we use two schemes, i.e., the expafunction and extended sinh-Gordon equation expansion(EShGEE)schemes.The general expafunction scheme was first proposed by Ali and Hassan in Ref.[25].Yan firstly proposed the extended sinh-Gordon equation expansion method in Ref.[26].They are two different techniques used for solving nonlinear partial differential equations.Both the methods are proposed to find the vast categories of exact wave solutions.Many applications are closely related to these two schemes.For example,different types of solitons of two nonlinear Schr¨odinger equations have been attained with the application of expafunction scheme,[27]analytical wave solitons of the modified Camassa–Holm model are gained with the use of this scheme.[28]Some optical solitons of a new Hamiltonian amplitude model have been achieved by applying the extended sinh-Gordon equation expansion scheme in Ref.[29].A new type of optical wave solutions of the Biswas–Arshed equation have been gained by using the EShGEE scheme.[30]Different kinds of soliton solutions including dark, bright, dark-bright, singular and other wave solutions of the Kundu–Eckhaus equation have been gained.[31]
We employ the Fitzhugh–Nagumo model that is much more important in biology and electronics.Different techniques have been applied to search the exact wave solutions of this model, e.g., some different types of exact wave solutions of this model have been gained by extended tanh-coth technique in Ref.[32], solitary and periodic wave solutions have been obtained by the exp-function scheme in Ref.[33],a new kind of analytical wave solitons has been achieved by this model with the help of sine-Gordon expansion technique in Ref.[34].
The fundamental purpose of the work is to search the new analytical wave solutions of the spacetime fractional Fitzhugh–Nagumo model via the expafunction and extended sinh-Gordon equation expansion schemes.
The motivation of this paper is to explain the effect ofM-fractional derivative on the solutions of the spacetime fractional Fitzhugh–Nagumo model, which are gained with the use of the expafunction and extended sinh-Gordon equation expansion schemes.Significance ofM-fractional derivative is that it fulfills both the properties of integer and fractional order derivatives.By using the extended sinh-Gordon equation expansion scheme, we can obtain the sech, csch, tanh and coth functions involving solutions.Using our schemes,we can observe some elementary relationship between fractional NLPDEs and other simple nonlinear ordinary differential equations.It has been found that with the use of simple schemes and solvable ordinary differential equations, different types of exact wave solutions of some complicated fractional NLPDEs can be easily obtained.The solutions attained are newer than the existing solutions in the literature.The achieved results may behave similarly to biological neurons which can be implementable on digital platforms.
The rest of this paper is organized as follows: In Section 2, we describe the model and present its mathematical analysis.In Section 3, we present the methods.In Section 4,we provide exact wave solitons of the model.In Section 5,we illustrate the model with graphics.Section 6, we provide conclusions.
2.Governing model and its mathematical treatment
Assume the (1+1)-dimensional nonlinear truncatedMfractional Fitzhugh–Nagumo model given as[32]
where
withEϒ(·)representing the truncated Mittag–Leffler function of one parameter given in Refs.[35,36];v=v(x,t)shows the wave profile,xandtrepresent the space and time variables,respectively;δdenotes the parameter.Equation(1)expresses a nonlinear reaction-diffusion model used in the transmission of nerve impulses as well as in biology as population genetics.It is also used in circuit theory.
Let us assume the following wave transformation:

We will find the new exact wave solitons using the following schemes.
3.Methods
3.1.The expa function scheme
This scheme is briefly explained in the following.Consider the nonlinear partial differential equation

Substitutingℓi(0≤i ≤n)into Eq.(11)and making it equal to zero,a system of equations is gained as follows:
with assistance of the achieved equations,we can gain analytical wave solutions of Eq.(7).
3.2.The EShGEE scheme
There are following main steps in this scheme.
Step 1 Assume a nonlinear fractional partial differential equation

The positive numbermis calculated by utilizing the homogenously balance method.Equation (17) is obtained from the sinh-Gordon equation as
From Ref.[40],we obtain the solutions to Eq.(18)as
here i2=-1.
Step 3 Substituting Eqs.(16) and (20) into Eq.(15), we achieve the equations consisting ofw′k(η)sinhl w(η)coshm w(η) (k= 0,1;l=0,1;m= 0,1,2,...).Substituting each coefficient ofw′k(η)sinhl w(η)coshm w(η) and make it equal to zero, we gain a set ofν,κ,α0,αj,andβj(j=1,2,3,...,m).
Step 4 After solving the achieved set of equations, one can gain the results forν,κ,α0,αj,andβj.
Step 5 From the gained results, i.e., Eqs.(19) and (20),we obtain the analytical wave solutions to Eq.(15)as follows:
Using this technique, we can obtain the sech, csch, tanh and coth functions involving solutions.
4.Analytical wave solutions
4.1.Using the expa function scheme
Form=1,Eq.(10)reduces to


whereλandτare given in Eq.(34).
4.2.Using the EShGEE scheme
Form=1,Eqs.(21),(22),and(16)reduce to
whereα0,α1,andβ1are undetermined.Substituting Eq.(38)into Eq.(4) we gain algebraic equations containingα0,α1,β1,and other parameters.By using the Mathematica tool,we obtain the following sets.
Set 1


whereλandτare given in Eq.(54).
Set 7
whereλandτare given in Eq.(69).
Set 12

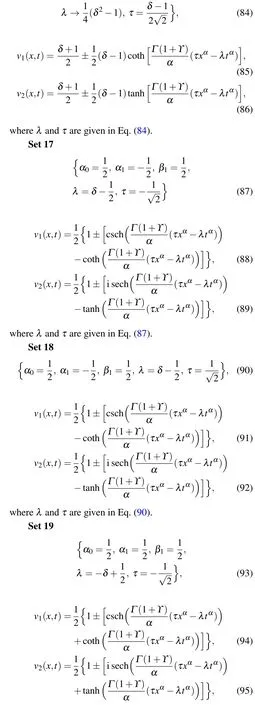
whereλandτare given in Eq.(93).
Set 20

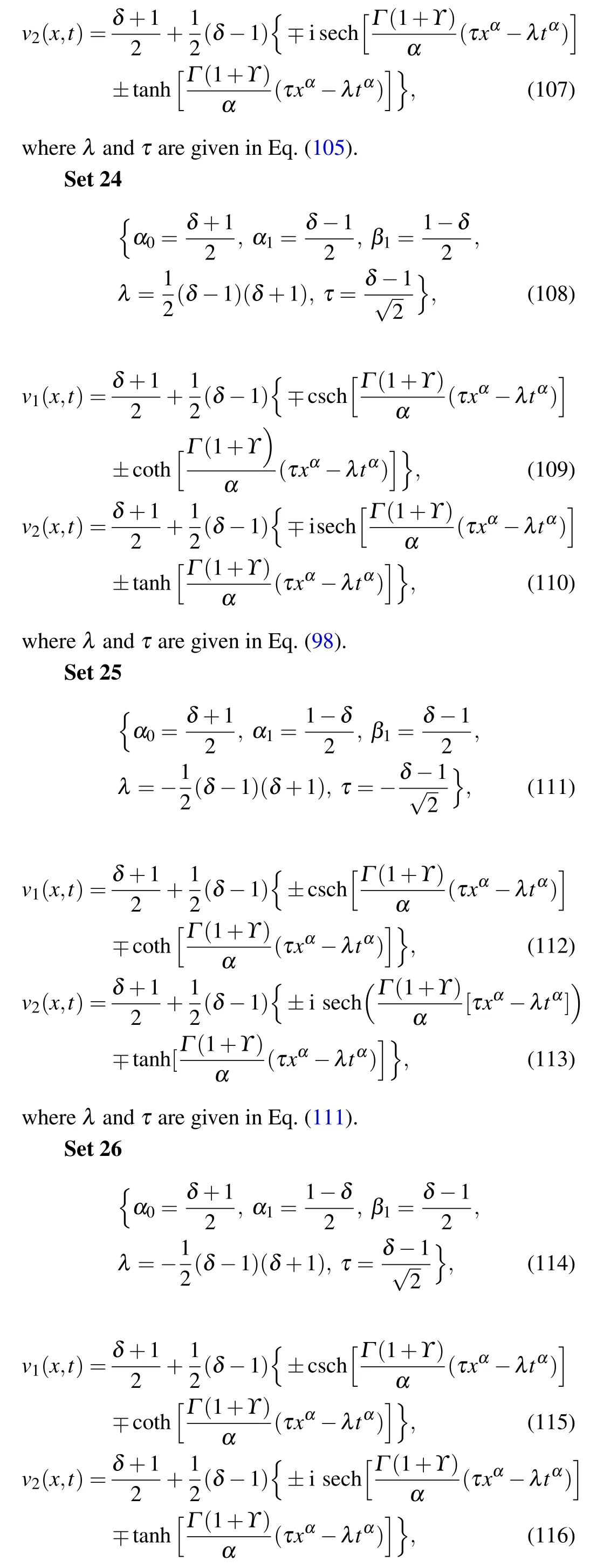
whereλandτare given in Eq.(114).
Set 27

whereλandτare given in Eq.(126).
Set 31
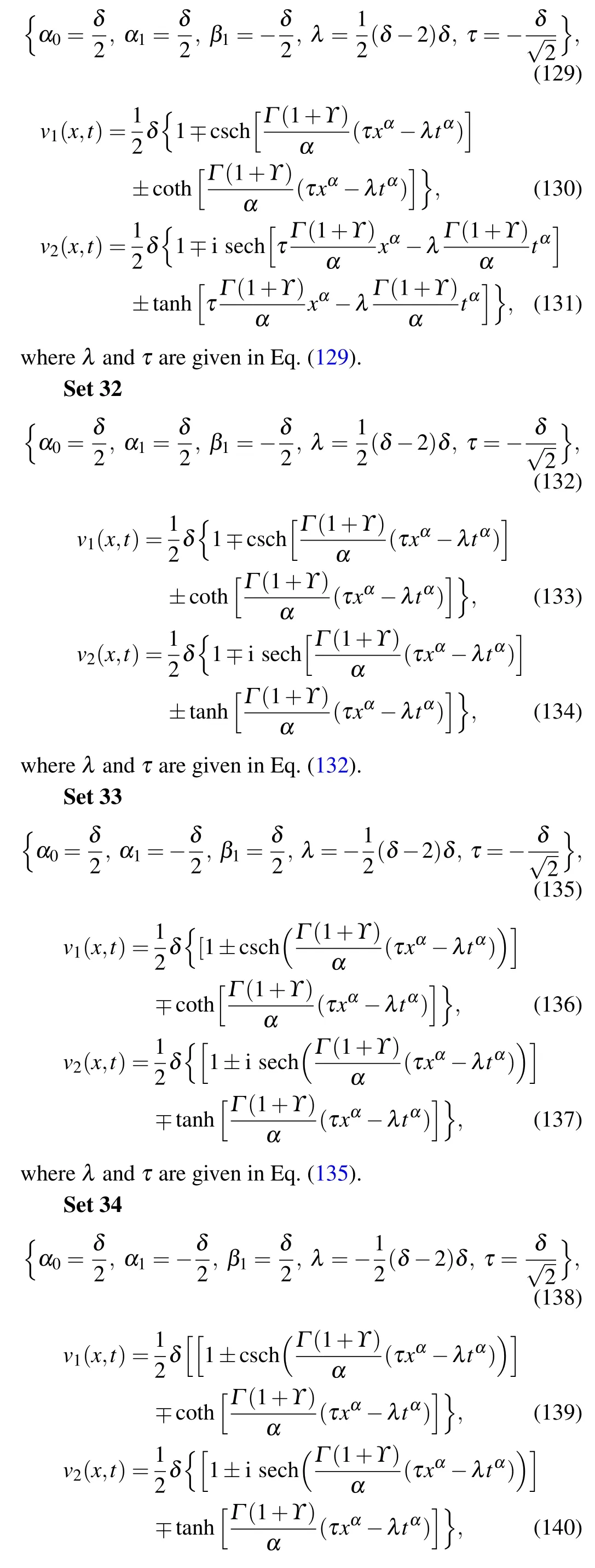
whereλandτare given in Eq.(138).
Set 35
whereλandτare given in Eq.(141).
Set 36
whereλandτare given in Eq.(144).
5.Physical explanation of solutions
In this section, some of our obtained traveling wave solutions are depicted in the following.Figure 1 shows a wave profile of|v1(x,t)|appearing in Eq.(25)withd=2,β0=0.2,β1=0.3,ϒ=1,δ=0.1,and-5 Fig.1.Wave profile of|v1(x,t)|appearing in Eq.(25)in 2D,3D,and contour. Fig.2.Wave profile of|v7(x,t)|appearing in Eq.(31)in 2D,3D,and contour. Fig.4.Wave profile of|v2(x,t)|appearing in Eq.(41)in 2D,3D,and contour. In summary, we gain the analytical wave solutions using the truncatedM-fractional Fitzhugh–Nagumo model and applying the expafunction and EShGEE schemes.The solutions gained involve the sech, csch, tanh and coth functions.These analytical wave solutions are gained and verified with the use of Mathematica software.These solutions do not exist in literature.Some of the solutions are demonstrated by 2D, 3D and contour graphs.This research may be helpful in the telecommunications field and other related waveguides.It is suggested that these two schemes are more applicable, reliable and significant to deal with fractional nonlinear partial differential equations.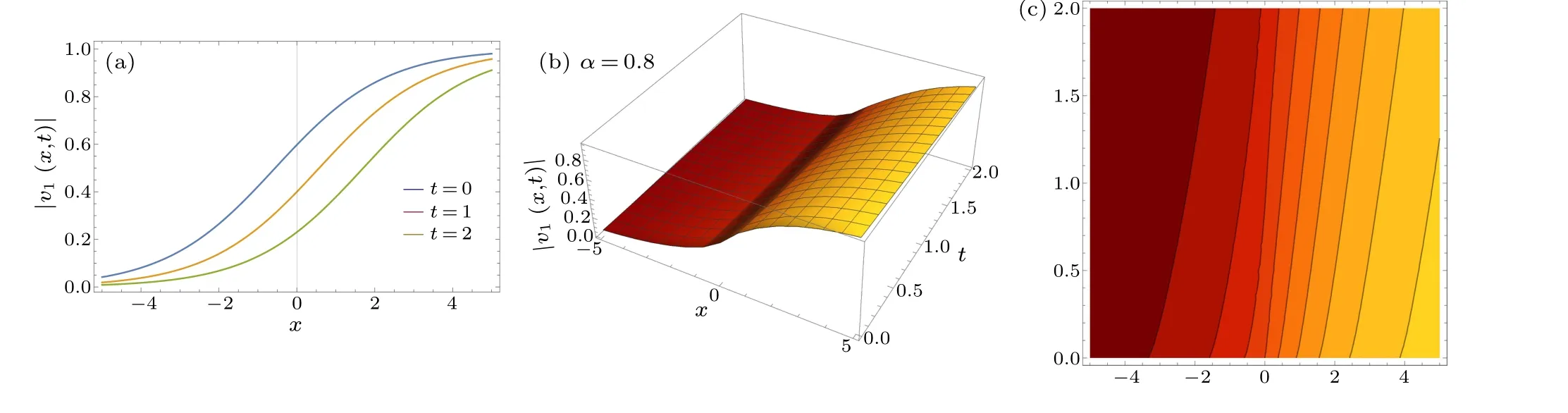


6.Conclusions
杂志排行
Chinese Physics B的其它文章
- Optimal zero-crossing group selection method of the absolute gravimeter based on improved auto-regressive moving average model
- Deterministic remote preparation of multi-qubit equatorial states through dissipative channels
- Direct measurement of nonlocal quantum states without approximation
- Fast and perfect state transfer in superconducting circuit with tunable coupler
- A discrete Boltzmann model with symmetric velocity discretization for compressible flow
- Dynamic modelling and chaos control for a thin plate oscillator using Bubnov–Galerkin integral method
