Detection of EEG signals in normal and epileptic seizures with multiscale multifractal analysis approach via weighted horizontal visibility graph
2023-12-02LuMa马璐YanLinRen任彦霖AiJunHe何爱军DeQiangCheng程德强andXiaoDongYang杨小冬
Lu Ma(马璐), Yan-Lin Ren(任彦霖), Ai-Jun He(何爱军),De-Qiang Cheng(程德强), and Xiao-Dong Yang(杨小冬),†
1School of Information and Control Engineering,China University of Mining and Technology,Xuzhou 221116,China
2Suzhou Vocational and Technical College,Suzhou 234000,China
3School of Computer Science and Technology,China University of Mining and Technology,Xuzhou 221116,China
4School of Electronic Science and Engineering,Nanjing University,Nanjing 210023,China
Keywords: epilepsy,EEG signal,horizontal visibility graph,complex network
1.Introduction
Epilepsy is a common chronic neurological disorder characterized by recurrent seizures,which are sudden and temporary disturbances and abnormalities in the electrical activity of the brain.These surges of abnormal electrical activity can temporarily impact a person’s behavior and can even consequence in loss of consciousness.[1]Status epilepticus is a prolonged seizure state, nevertheless there can be numerous difficulties in detecting epilepsy,as symptoms can be varied and not always obvious.In addition,electroencephalogram(EEG),which aids in the diagnosis of epileptic disorders,is performed by medical professionals specializing in neurology due to its specialized nature but is less efficient due to the sporadic and recurrent nature of seizures.The limitations of conventional tools have promoted the development of innovative methods,and rapid and cost-efficient diagnosis of seizures is the future tendency.
The studies on seizure detection have focused on time–frequency analysis and nonlinear dynamics.[2]The advantage of the time–frequency analysis method[3–5]is reflected in the instantaneous frequency and amplitude change capture.[6]Nonlinear analysis methods explore the differences between patients and healthy individuals by extracting nonlinear features such as entropy,[7,8]Hurst exponent,[8]Lyapunov exponent,[9]and multifractal characteristics.[10]Due to the complex nature of EEG signals,nonlinear dynamics has lately been widely used to study epilepsy detection.In recent years,the use of complex network methods to analyze time series,is the latest direction of nonlinear dynamics development.In 2006, Zhang and Small for the first time realized the conversion of pseudoperiodic time series into complex networks and analyzed the difference in the topological statistical characteristics of chaotic signals and Gaussian white noise complex networks.Based on the proposed complex network construction algorithm, they analyzed the characteristics of complex networks on a variety of time series and found time series of different properties.In 2008, Lacasaet al.[11]proposed visibility graphs(VG)to establish a new connection between time series and complex networks.Subsequently, Luqueet al.[12]proposed a more simplified structure of horizontal visibility graphs (HVG), which preserved the nature of the time series so that the nodes in the horizontal visibility would have“inferior visibility” than their visible counterparts.[13]Nowadays, VGs and HVGs are widely used algorithms in time series construction graphs, which provides a fresh perspective for time series analysis.Electroencephalogram(EEG)signal,as a time series composed of potential change patterns, can be applied to study brain function and mental state.In the study of complex network analysis of EEG signals, the sampled EEG signals are converted into the corresponding complex networks, so as to realize the modeling of the brain system and analyze the properties of complex networks to reflect the dynamic characteristics of the brain system.Zhuet al.[14]defined the weight values of HVG and extracted the network parameters of weighted HVG (WHVG) from the EEG signal to detect epilepsy.Bhaduriet al.[15]measured the scale-free nature of the VGs mapped by the EEG signals and detected the difference between epileptic and normal signal by analyzing the change in its value.Supriyaet al.[16]set the weight value for the connected edges of the VG to be the visible angle between the two nodes,and then used this weighted VG(WVG)algorithm to analyze the epileptic EEG signal and used machine learning for network features for automatic seizure detection.Mohammadpooryet al.[17]used entropy for the analysis of epileptic EEG signals based on the WVG proposed by Supriyaet al.
On the other hands,fractal is a mathematical concept that describes the structure of complex networks with self-similar patterns.In 2005,Songet al.[18]revealed the degree distribution of the network follows a power law,which means that the number of nodes with a given degree decreases as the degree increases, following a power function.Network multifractal analysis is an extension of the fractal analysis that allows the study of the complexity of the network structure by considering different fractal scaling exponents in different regions of the network.[19]Furuya and Yakubo[20]performed multifractal analysis of the network using an improved compactboxburning algorithm in the study of Songet al.[18]Meanwhile,Wanget al.[21]proposed the box-covering algorithm and used the algorithm to calculate the generalized fractal dimensions of theoretical networks and real networks.Immediately following, Liuet al.[22]adapted the Sandbox algorithm[23]for signal fractal analysis to multifractals of complex networks with a lower time complexity compared to previous algorithms.Pav´on-Dom´ınguezet al.[24,25]analyzed multifractals of networks with another fixed-quality approach.The existing network multifractal studies only concern to limited scales that may loss some details.We now propose the multiscale multifractal analysis (MMA) of the networks to research the EEG time series,which could greatly enrich the information of their fractal structure.
In this study, we work on weighted horizontal visibility graphs(WHVG)algorithm to map EEG signals into complex networks, which focus more on the topology and scalefree properties of the networks.Based on the research ideas of Bhaduriet al.,[15]novel scale-free parameters of fractality and multifractality are extracted to comprehensively characterize the WHVG.The fractality and multifractality could indicate the self-similarity and complexity of the network, but they have some problems in the scale-free intervals.Multiscale multifractal analysis of the is originally proposed by Gierałtowskiet al.[26]as an improvement to the multifractal detrended fluctuation analysis(MF-DFA)method.We refer to their ideas and adapt it to the multifractal analysis of the network,which can capture more comprehensive nonlinear information based on fractal and multifractal algorithms.In Section 2, we describe these methods and also present the data used in this study.In Section 3, we depict the analysis and results of the study, which contains comparisons of the fractal and multifractal parameters.Then the MMF analysis is taken a step further and contrasted.Finally,the extracted network parameters are trained through neural network(NN).The classification and identification of three EEG signals, namely health,interictal phase and ictal phase,are realized with 99.0%classification accuracy.In Section 4,we draw conclusions.
2.Materials and methods
2.1.Dataset
The study used the dataset[27]from the University of Bonn, Germany, which contained EEG signals from healthy and epileptic subjects.The dataset is comprised of five subsets,each with 100 single-lead EEG signals.These segments have a duration of 23.6 seconds,a sampling rate of 173.61 Hz,and are removed from interference.Sets A and B are surface EEG recordings of five healthy volunteers with eyes open(A) and eyes closed (B) in a relaxed state.Sets C, D, and E are EEG recordings from five patients with epilepsy.Segments in set C were recorded activity measured from the hippocampal formation in the opposite hemisphere of the brain during seizure-free intervals, and those in set D from within the epileptogenic zone.Set E contained seizure activity within the epileptogenic zone.
To attain a precise classification of healthy,interictal and ictal EEG signals, we determine three of these subsets and name the sets B,D,and E as health,interictal phase,and ictal phase, respectively.Examples of the EEG signals in each set are shown in Fig.1.

Fig.1.Examples of three different types of EEG signals, from top to bottom,are the healthy EEG signal,the interictal EEG signal,and the ictal EEG signal.
2.2.Weighted horizontal visibility graphs(WHVG)

2.3.Fractality and multifractality of the network
As mentioned in the introduction,the topology of a complex network is fractal and self-similar at different scales,i.e.,the topology of the overall network is similar to the topology of its parts.In the case of multifractality,different values ofαidentify different components of the network structure,which means that the spectrumf(α) can be formed.[28]We use the Sandbox algorithm proposed by Liuet al.[22]to study the multifractality of WHVGs.The algorithm can be described as follows:
(i) Set the radiusrof sandbox to cover the nodes in the graph,letr ∈[rmin:rmax],and this study uses the diameter of the graph asrmax,and the average value of the weights asrmin.The interval forris also taken as an average of the weights to ensure that the number of sandboxes covering different graphs is appropriate.
(ii)Select each node of the graph as the center of the sandbox,and starting with the center of the sandbox,search for all nodes less than or equal torand cover them.Count the number of nodes in each sandbox of radiusr,denote asM(r).The equation is

whereD(0),D(1), andD(2)are the fractal dimension, information dimension,and correlation dimension of the network,respectively.
The singularity spectrumf(α)is related toτ(q)through the Legendre transformation as
The curveα ∼f(α) is the singular spectrum of multifractality.The quantity of singular spectrum width ∆α=max(α)-min(α) describes the inhomogeneity of the probability distribution measured by the total fractal structure and determines the degree of multifractality.The larger the value of ∆α,the stronger the corresponding multifractal degree.[28]Theq-values for this study are chosen in the range of-20 to 20,as shown in Fig.3(b).
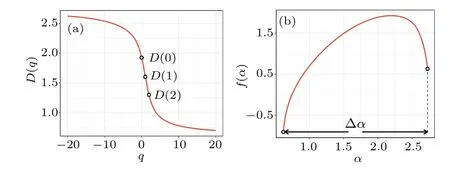
Fig.3.Multifractality of EEG-mapped WHVGs.(a) The red curve is the generalized fractal dimension for an EEG-mapped WHVG in the interictal phase, and D(0), D(1), and D(2) are the fractal dimension, information dimension, and correlation dimension of the network, respectively.(b) The red curve is the singular spectrum of multifractality for an EEG-mapped WHVG in the interictal phase, and the width of the singular spectrum is∆α =max(α)-min(α).
2.4.Multiscale multifractality of the network
In multifractal analysis,there are occasional cases of accuracy degradation due to unreasonable choice of scale-free intervals.The existing methods could solve it, but there is a possibility that some information would be discarded.Some methods of selecting scale-free intervals usually choose intervals with good linearity and discard other slightly weaker information.Therefore, we integrate the multiscale approach into the multifractal analysis of the network, preserving all information while retaining well-fitting scale-free intervals,which improves the accuracy of the analysis and classification process.
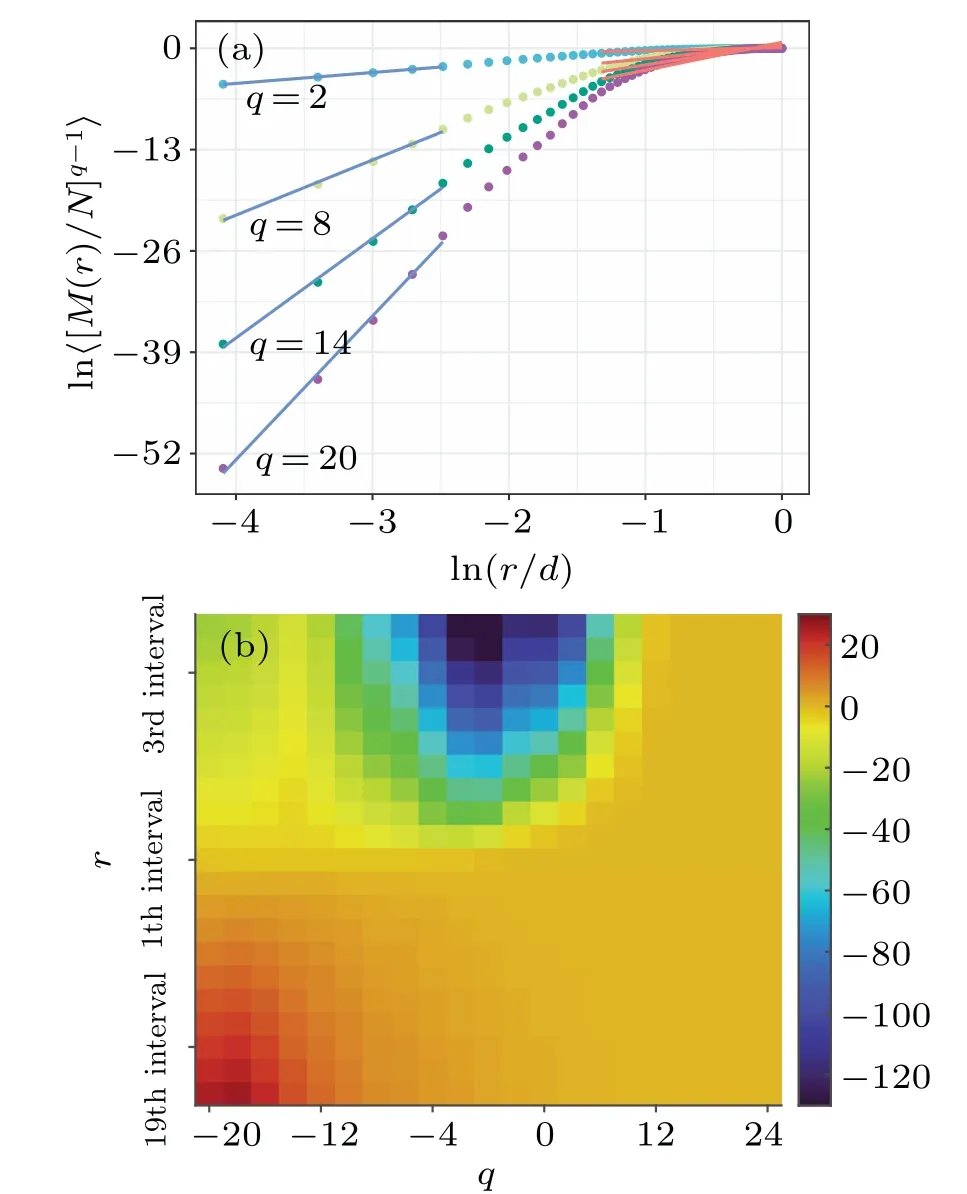
Fig.4.The MMA of EEG-mapped WHVGs.(a)The scatter from top to bottom are τ(q)fitted plots for q=2,8,14,and 20 in interictal phase.When the fit is performed, the results of the first part of the fit (blue line) have a large difference from the results of the last part of the fit(red line).(b)The MMA using interval=rmax/6 and spacing=(rmax-rmin)/20 in interictal phase.The n-th square of the fixed q value represents the τ(q)fitted value within the interval from rmin+spacing×(n-1).
As shown in Fig.4(a),we can see that the fitted values of its multifractal scale factors are different within different interval windows.This makes it inevitable that errors exist when we use all the points for the fitting analysis and requires us to adopt the idea of multiscale.For multiscale multifractal analysis(MMA),we define the size and start position of the fitting interval.
Figure 4(b) shows the two-dimensional relationship matrix between the fitted intervals and the scale factorq-values.Each square represents the fitted value within the fitted interval corresponding to thisq-value.The vertical coordinate is the starting position of the fixed fit interval for the size of the moving fitted interval.In this way, the problem of different fitting results for different intervals appearing in Fig.4(a) is solved.For the length of the fitted interval we use 1/6 of the diameter, namely interval=rmax/6.The start position is related to the spacing and the choice of spacing is related to the density of the grid we need, and this study uses 21 fitted intervals,then spacing=(rmax-rmin)/20.As can be seen from Fig.4(b), the region where the maximums located is concentrated in the lower left corner,and the region where the minimums are located is concentrated in the middle above.
3.Analysis and results
The EEG signals from the University of Bonn have been eliminated from possible interferences such as muscle artifacts and blink artifacts.Therefore,in this study,we only performed a simple filtering process to extract the 0.3 Hz–30 Hz band.For the three EEG sets of health, interictal phase, and ictal phase, there are 100 signals in each set and each segment is selected for its 4096 sequential sampling points.To reduce the time complexity, we divide each signal into 4 segments and map them into WHVGs.In the parametric analysis, the network features extracted from the 4 segments are averaged to represent the identity of that signal for analysis, which facilitates the strengthening of its own characteristics.
3.1.Fractal and multifractal analysis of EEG-mapped WHVGs
First, we explored the differences among different EEG sets by examining the structural features of WHVGs.We compared the ∆αof the three sets of EEG-mapped WHVGs during healthy,interictal,and ictal phases,as shown in Fig.5.As can be seen from Fig.5,EEG-mapped WHVGs in the health have a stronger degree of multifractality compared to the other two sets, while those in the ictal phase have a weaker degree of multifractality,and the interictal multifractality is between the two sets.The degree of multifractality decreases with the degree of EEG signal disturbance.
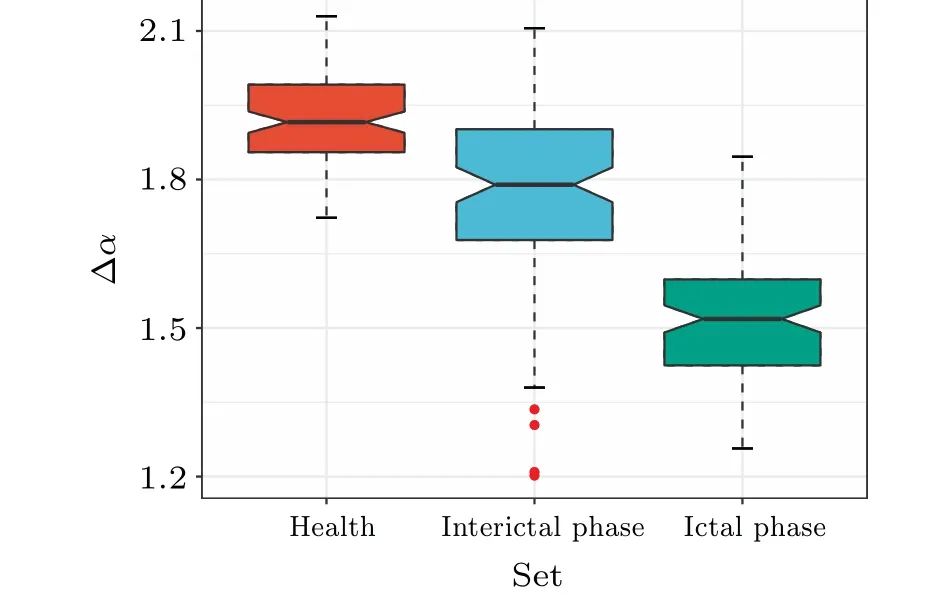
Fig.5.Box plots of ∆α of healthy,interictal,and ictal EEG-mapped WHVGs.The EEG signals of health have a stronger degree of multifractality and those in the ictal phase have a weaker degree of multifractality.

Fig.6.Box plots of ∆α of healthy, interictal, and ictal EEG-mapped WHVGs.The EEG-mapped WHVGs in the interictal phase smaller dimensions.And as the value of q increases, the average D(q) of healthy EEGmapped WHVGs decreases faster compared with that of ictal phase.
We also compared the three dimensions of the EEGmapped WHVGs in the healthy, interictal, and ictal phases,as shown in Fig.6.As shown in Fig.6, the EEG-mapped WHVGs in the interictal phase have smaller dimensions compared to the other two sets.As the value ofqincreases,the averageD(q)of healthy EEG-mapped WHVGs decreases faster compared with that of ictal phase, and the average fractal dimensionD(0) is similar forq=0, while the average correlation dimensionsD(2) of healthy EEG-mapped WHVGs is significantly smaller than that of ictal phase whenq=2.We can also see from the decreasing trend ofD(0)toD(2)that the dimensions of healthy individuals decrease faster, indicating a greater variation, implying a broader range of multifractal spectra.
3.2.Multiscale multifractal analysis of EEG-mapped WHVGs
Then we performed MMA on three sets of signals.Figure 7 shows the average values of MMA for the three sets of EEG-mapped WHVGs.In the region where the maximums are located (dark red), it is clear from the figure that in the ictal phase there has deeper values and a greater range compared to the other two sets, in the interictal phase there has lighter values and a smaller range, and in the healthy phase the values and range are between the other two sets.In the region where the minimums are located(dark blue),it is clear that in the healthy phase there has deeper values and a greater range compared to the other two sets, in the ictal phase has lighter values and a smaller range, and in the seizure phase the values and range are between the other two sets.And it is observed that the minimums region of EEG-mapped WHVGs in ictal phase is more concentrated in the direction of largerqvalue compared to the other two sets.The results of the MMA of different signals have different detailed information that we cannot represent by one or a few parameters.We think it makes sense to use the convolution operation for MMA to extract the most adequate information possible.
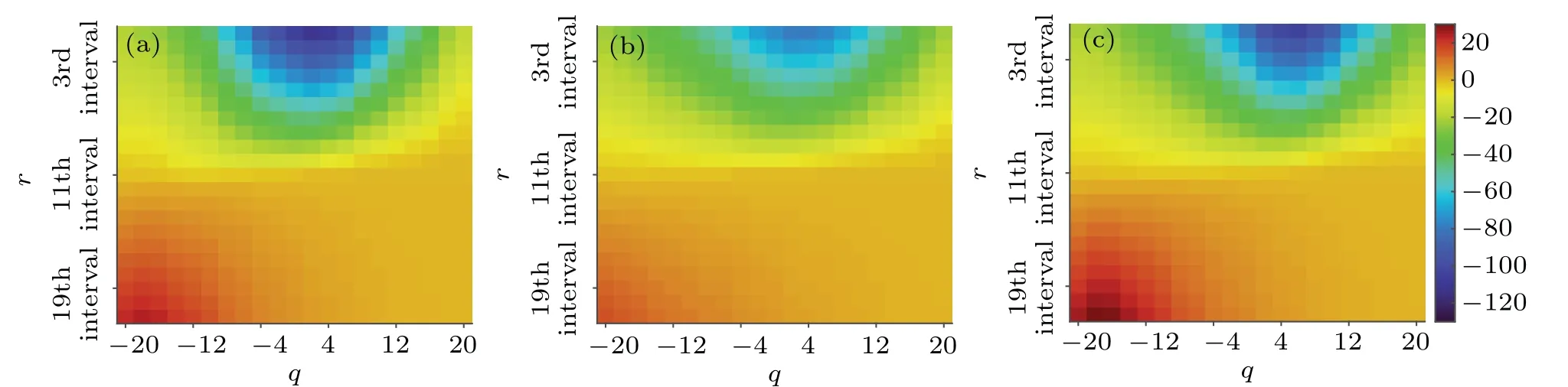
Fig.7.The average values of MMA for the three sets of EEG-mapped WHVGs.(a) The average values of MMA in health.In the region where the minimums are located(dark blue),it has deeper values and a greater range compared to the other two sets.And in the region where the maximums are located (dark red), it is between the other two groups in terms of depth and range.(b) The average values of MMA in interictal phase.It has lighter values and a smaller range in the region where the minimums and maximums are located compared to the other two sets.(c) The average values of MMA in ictal phase.It has deeper values and greater range in the region where the maximums are located compared to the other two sets.
3.3.Classification results
The parameters extracted from each EEG-mapped WHVG are eventually used in this study for multi-classification using neural network(NN)algorithms.Figure 8 depicts the block diagram of the proposed model.We use the dataset of the University of Bonn for validating the model and the whole process is divided into three stages: The first is the mapping of signal,we filter the signal with a bandpass from 0.3 Hz to 30 Hz and map it to WHVG.The second stage is the feature extraction from WHVG,including fractality,multifractality and multiscale multifractality of the network.The parameters of fractality and multifractality are represented by the average values of the segments,respectively,and the parameter of multiscale multifractality is represented by the concatenation of the 4 segments.The final stage is parameter fusion and classification to obtain the final detection result.

Fig.8.Block diagram of the proposed model.The model is constituted by three panels, i.e., network construction, parameters extraction,and classification.The filtered segmented signal is mapped to WHVG.The fractal, multifractal, and MMF parameters are extracted, where the fractal and multifractal parameters are averaged to form a vector and the MMF parameters are convolved and then concatenated.The classification result is obtained by a fully connected network after all parameters are concatenated together.

Fig.9.Confusion matrix of NN classifier, the rows of the confusion matrix represent the true values and the columns represent the predicted values.The diagonal values are the result of the correct classification and the sum is 297,the accuracy rate is 99.0%.
We obtained classification results by 10-fold crossvalidation,and the results are given by Fig.9.The diagonal of the matrix represents the number of true positives, the darker the color means that the model is better at correctly predicting the positive class.From the calculation,the classification accuracy rate is 99.0%
Table 1 provides a comparison of this study with other network-related previous studies.In comparison, our proposed model algorithm possesses the highest accuracy.This reflects the large accessibility of multifractals as well as MMA in extracting HVG feature information.The study has some accuracy advantages compared to other studies related to feature extraction.The results of this comparison are given by Table 2.Among them, the accuracy of the multifractal analysis of the frequency sub-bands by Sikdaret al.[10]is higher than ours because the model of this study employed more parameters than ours.This shows that our approach is effective.

Table 1.Comparative analysis of accuracy with existing network-related works that was studied using three sets of EEG data from the Bonn dataset: healthy eyes open(set A),healthy eyes closed(set B),interictal(set D),and ictal(set E)phases.

Table 2.Comparative analysis of the accuracy with other existing parameter extraction efforts that was studied using three sets of EEG data from the Bonn dataset: healthy eyes open(set A),healthy eyes closed(set B),interictal(set D),and ictal(set E)phases.
4.Conclusions
In order to realize the effective detection of epilepsy, we proposed a new method for analyzing nonlinear time series.This study uses WHVG algorithm to map EEG signals into complex networks and extracts novel parameters.The structures of these networks are studied by calculating fractality,multifractality,and multiscale multifractality of each network to explore the nonlinear dynamical properties of the EEG signals inherited in networks.The fractality and multifractality of the networks effectively characterize their self-similarity and complexity properties, and MMA extends fractality and multifractality to make information more comprehensive.Finally,tensors consisting of these parameters are classified using NN classifiers and the results show that the method can significantly differentiate among healthy, interictal, and ictal EEG signals with an accuracy of 99.0%.The results reflect the effectiveness of WHVG as well as fractality,multifractality,and multiscale multifractality in extracting the potential dynamic characteristics of EEG signals.This also has implications for the analysis of other multifractal chaotic time series,e.g.,ECG signals,financial time series,etc.
There are still some areas to be further improved and expanded in this study.The sub-bands of EEG signal(i.e.,δ,θ,α,β,andγbands)can be further combined in future studies.These sub-bands have characteristic frequency ranges and distributions.They are often associated with different functional states of the brain, considering the characteristics of its frequency sub-bands may result in more comprehensive range of features and higher accuracy of classification.
Acknowledgements
Project supported by the Xuzhou Key Research and Development Program (Social Development) (Grant No.KC21304) and the National Natural Science Foundation of China(Grant No.61876186).
杂志排行
Chinese Physics B的其它文章
- Optimal zero-crossing group selection method of the absolute gravimeter based on improved auto-regressive moving average model
- Deterministic remote preparation of multi-qubit equatorial states through dissipative channels
- Direct measurement of nonlocal quantum states without approximation
- Fast and perfect state transfer in superconducting circuit with tunable coupler
- A discrete Boltzmann model with symmetric velocity discretization for compressible flow
- Dynamic modelling and chaos control for a thin plate oscillator using Bubnov–Galerkin integral method
