Effect of local wall temperature on hypersonic boundary layer stability and transition

Ruiyang Lu(鲁锐洋) and Zhangfeng Huang(黄章峰)

Department of Mechanics,Tianjin University,Tianjin 300072,China

Keywords: hypersonic boundary layers,direct numerical simulations,linear stability theory

1.Introduction

In hypersonic flows,the laminar-to-turbulent transition is vital for aerodynamic and aerothermal designs of vehicles,as it is accompanied by a significant increase in skin friction and heat transfer.Generally, a natural transition process can be divided into four stages: receptivity,linear instability,nonlinear instability, and turbulence.Accurate prediction of transition onset position is helpful for improving the economics of vehicles, and is a key technology for hypersonic vehicle development.[1]

Early studies on stability and transition largely focused on low-velocity flows, where the dominant instability in the boundary layer comes from the Tollmien–Schlichting (T–S)waves.As the flight speed increases, the hypersonic boundary layer transition becomes significantly different from subsonic or supersonic flows, and a new instability mechanism emerges.Mack made the most important contribution to the understanding of compressible flow stability.[2]He first found the existence of higher-order modes in supersonic flow,which are known as the Mack modes.Normally, the instability disturbance mode with the lowest frequency is called the second mode and the T–S wave is called the first mode.At higher Mach numbers, the two-dimensional Mack mode wave becomes the most unstable mode disturbance, making it more important than the first mode.[3]In hypersonic flows, many experimental and numerical results have confirmed that the second mode is dominant in terms of the transition.[4–8]

The surface temperature of a vehicle tends to remain constant over a long flight, but it may still have a certain temperature distribution.The thermal protection systems of such vehicles typically have elements with different heat conductivity and emissivity.The connections between these elements, as well as weak shockwaves hitting the boundary layer,will cause the wall temperature to jump.[9]Active thermal protection systems may even produce partially heated or cooled regions on the surface, and these thermal nonuniformities significantly affect the excitation and evolution of unstable modes within the boundary layer, and ultimately the transition.[10,11]Laminar-flow control (LFC) has been a hot topic in the aerospace field in recent years.The main idea of LFC is to reduce the initial amplitude of the dominant unstable mode during the receptivity stage or to reduce the growth rate during the linear instability stage.[12]Typically, LFC can be achieved by introducing localized surface imperfections such as surface suction[13]or rough elements.[14,15]Soudakovet al.[16]performed two-dimensional direct numerical simulation(DNS) of a Mach-6 flat plate boundary layer with wall temperature jumps, and found that these temperature jumps significantly affect the stability and receptivity of the boundary layer.This proves that localized wall temperature changes due to surface imperfections may enable LFC.

Most early studies on wall temperature focused on boundary layers with uniform wall temperature distributions.For subsonic boundary layers, wall cooling inhibits the disturbance growth[17]and wall heating promotes the disturbance growth.[18]For supersonic boundary layers, Mack[3]found that wall cooling,while significantly inhibiting the first mode,further enhances the instability of the second and other higherorder modes.These conclusions have been confirmed by many experimental and computational results.[19,20]

Although some studies have been conducted on nonuniform wall temperature distributions in recent years, there is still less research compared to those on uniform temperature distributions.For the supersonic boundary layer, Zhouet al.[21]used local cooling to control oblique breakdown in the supersonic boundary layer.The oblique breakdown could be effectively controlled by using local cooling strips, with a lower cooling temperature and wider cooling width producing a more pronounced transition delay.The main reason for the delay is that the local cooling stabilizes the first mode fundamental oblique waves.

Concerning hypersonic boundary layers,the situation become intricate when considering various geometries and wall temperature distributions.Polivanovet al.[22]conducted a study on the impact of two/three-dimensional cooling or heating elements on the stability and transition of a flat plate boundary layer.Their results show that local cooling delays the transition,and that the three-dimensional effect of the cooling element is relatively weak.Bountinet al.[23]experimentally investigated the effect of heating or cooling at the nose of a cone on the stability of the hypersonic boundary layer.For a sharp cone,heating/cooling at the nose caused the flow to become more unstable/stable.The opposite effect was observed for a blunt cone,where heating inhibits the second mode,thus stabilizing the flow, and cooling has the opposite effect.Fedorovet al.[24,25]conducted experimental and numerical investigations of a Mach-6 sharp cone boundary layer with local cooling and heating.They found that local cooling delayed the transition and local heating promoted the transition.Zhaoet al.[26]performed DNS to study the effect of local heating or cooling strips on the second mode in the hypersonic boundary layer from a receptivity perspective.The results indicate that the relative location of a local heating/cooling strip and the synchronization point significantly affect mode S.The unstable mode is amplified when the heating strip is located upstream of the synchronization point,and the effect is reversed when the heating strip is placed downstream.Based on the study of Zhaoet al.,Batista and Kuehl[27]investigated the effect of the local wall temperature on the second mode using parabolized stability equations and found that a combination of upstream cooling and downstream heating best suppressed the second mode.Based on the asymptotic theory, Zhao and Dong[28]investigated the effect of the local wall temperature on the Mack modes in a supersonic or hypersonic boundary layer.The results showed that the local wall temperature could change the mean flow in a similar manner to a rough element.However, the former causes more complex interactions with the Mack modes and generates different phenomena.

The results outlined above show that, for different models or different locations,changing the local wall temperature seems to produce different effects and specific rules are difficult to determine.For sharp cones,local changes in wall temperature have the opposite effect on the transition to a uniform change in wall temperature.To use the local wall temperature for LFC, it is necessary to find the reason for this inconsistency.Thus, this paper describes the use of linear stability theory (LST) and DNS, combined with experimental results,to investigate the effects of local wall temperature on stability and transition,and identify the underlying physical mechanisms.After determining the reasons for the above-mentioned inconsistency,LFC is applied by changing the location of local wall heating and the degree of cooling/heating.Unlike most previous studies,this paper not only focuses on unstable waves with specific frequencies, but also studies the combined effect of local wall temperature on multiple-frequency unstable waves from an overall perspective.Thus, the research results are more instructive for practical engineering problems.

2.Mathematical descriptions

2.1.Physical model

The physical model used in this paper is a 7◦half-angle cone with a sharp nose.The cone length is 500 mm and the radius of the nose is 0.07 mm.The simulation conditions are the same as the experimental conditions in a quiet wind tunnel,[24]with a freestream Mach number ofMa= 6, unit Reynolds number ofRe=9×106m-1, and freestream temperature ofT∞=44.24 K.Fedorovet al.[24]found that the nonuniform temperature distribution at the boundary is smooth,so the wall temperature is specified as

wherexs1andxs2are the upstream and downstream boundaries of the wall temperature change,respectively.Except for the local wall temperature change section, the wall temperatureTwb=300 K.∆This the magnitude of the wall temperature change andTlis the local wall temperature.The specific wall temperature distributions considered in this study are listed in Table 1.

Name xs1 (mm) xs2 (mm) ∆Th Tl Base– – – –P125C50 125 200 -250 50 P125C100 125 200 -200 100 P125C150 125 200 -150 150 P125C200 125 200 -100 200 P125C250 125 200 -50 250 P125H350 125 200 50 350 P125H400 125 200 100 400 P125H450 125 200 150 450 P125H500 125 200 200 500 P200C150 200 275 -150 150 P325C150 325 400 -150 150 P425C150 425 500 -150 150 P200H450 200 275 150 450 P325H450 325 400 150 450 P425H450 425 500 150 450

2.2.Governing equations

The baseflow is obtained by solving the two-dimensional axisymmetric dimensionless Navier–Stokes equations using the finite difference method.The specific expressions are as follows:

wheretmeans time,xindicates the streamwise coordinate,andrindicates radial coordinate.In addition,Tis temperature,pis the pressure,ρis the density,uandvdenote the streamwise velocity component and the radial velocity component respectively,τis the viscous stress,andesis total internal energy;γis the specific gas ratio,Pris the Prandtl number,kis the heat conductivity, andµis the dynamic viscosity calculated using Sutherland’s law.Wis the source term due to the axisymmetric form.Uis the conservative flux vector,EandFare the convective flux vectors in the streamwise direction and radial direction respectively,EvandFvare the viscous flux vectors.The governing equation has been dimensionless in this way:the coordinates are dimensionless by reference lengthLref,velocityU∞, densityρ∞, pressureρ∞U2∞, temperatureT∞, viscosityµ∞,heat conductivityk,and timeLref/U∞.The dimensionless parameterReis given byRe=ρ∞U∞Lref/µ∞, Mach numberMa∞is given byMa∞=

The Navier–Stokes solver employs a standard third-orderaccurate Runge–Kutta method for the time integral.In particular, the derivatives of the viscous and source terms are calculated by sixth-order central differences, and the derivatives of the convective terms are calculated by the fifth-order WENO scheme.After verifying the grid-independence of the numerical scheme, a computational grid of 700×400 is chosen, where half of the grid points in the normal direction are located within the boundary layer.Figure 1 compares the baseflow profile calculated in this study with that calculated by Fedorovet al.[24]The profiles match well, thus demonstrating the reliability of our program.

2.3.Linear stability analysis

LST is based on the small disturbance and parallelism assumptions.The nonlinear terms in the equation and the variation of the baseflow along the streamwise direction are neglected.The linearized disturbance equation for a small disturbance reads

whereα,β,andωare the streamwise wavenumber,spanwise wavenumber, and frequency, respectively, and c.c.represents the complex conjugate.An eigenvalue problem can be obtained by substituting the above equation into the disturbance equation.In this paper,we use a spatial model withωas a real number,αandβas complex numbers.For two-dimensional waves,β=0 and-αiis the growth rate.The eNmethod based on LST definesNas

whereσ=-αiis the growth rate andx0is the starting position of the integral.

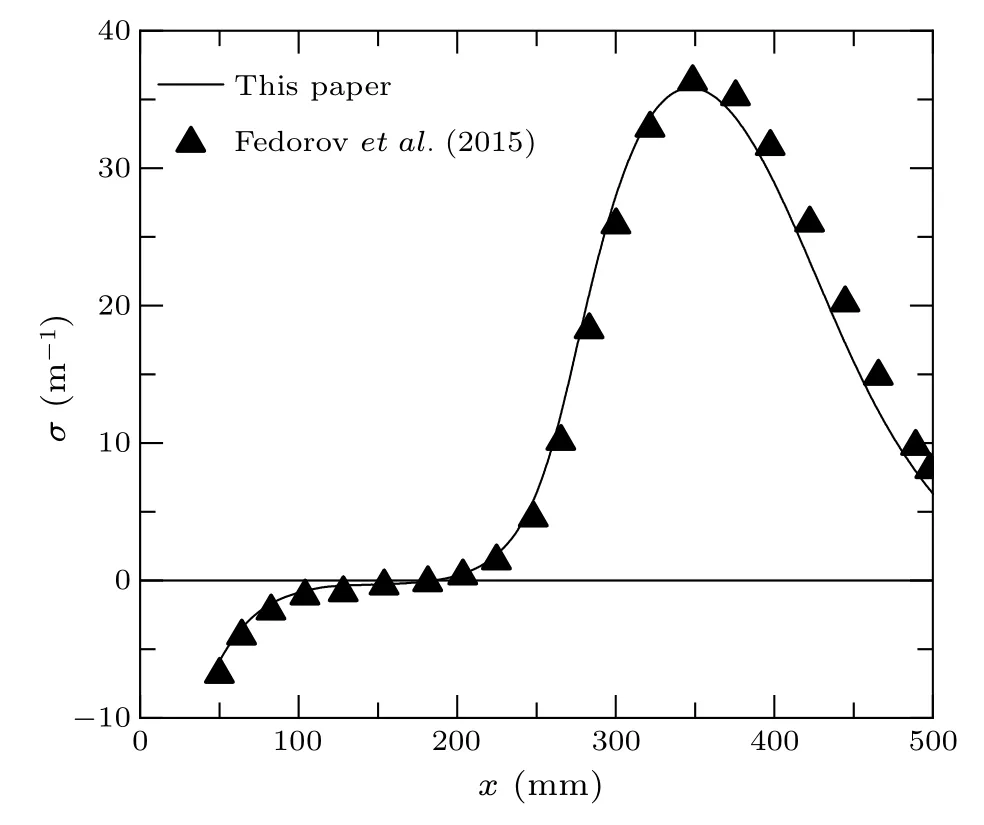
Figure 2 shows the growth rate off=180 kHz unstable waves.The results obtained here agree well with the results in literature,demonstrating the reliability of our LST program.

3.Results and discussion

3.1.Baseflow and stability analysis

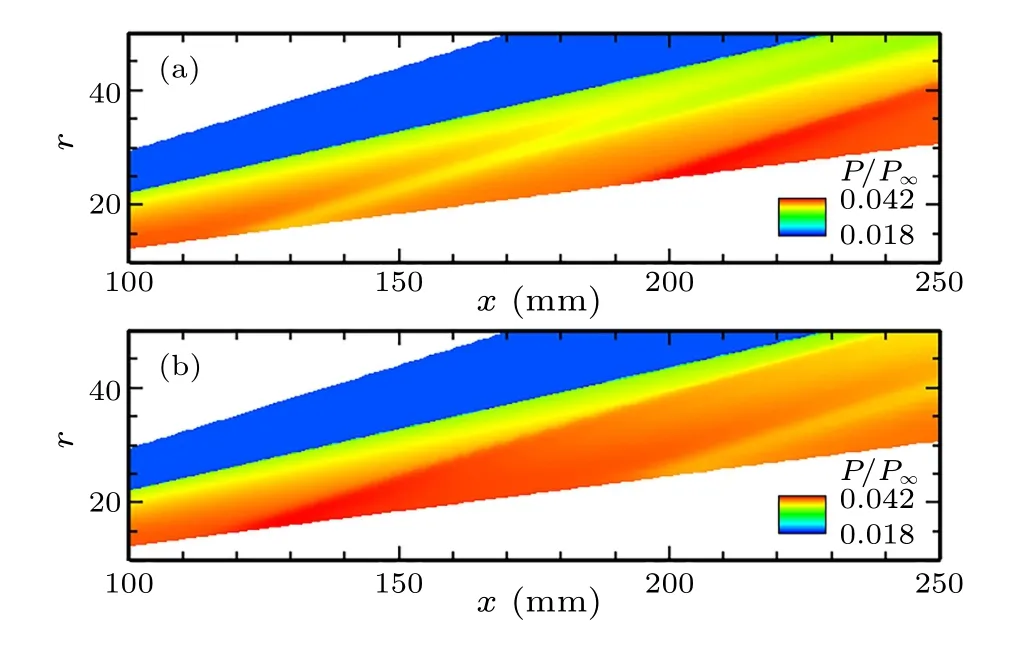
Figure 3 shows the nominal thickness of the boundary layer under different conditions.Clearly, cooling/heating makes the boundary layer locally thinner/thicker.When the wall temperature becomes uniform,the boundary layer thickness recovers quickly and approaches the boundary layer thickness of the base case.Figure 4 shows the pressure distributions for P125C150 and P125H450.In the case of wall cooling,an expansion wave appears at the start of cooling and a compression wave at the end of cooling.The phenomenon of heating produces the opposite effects.

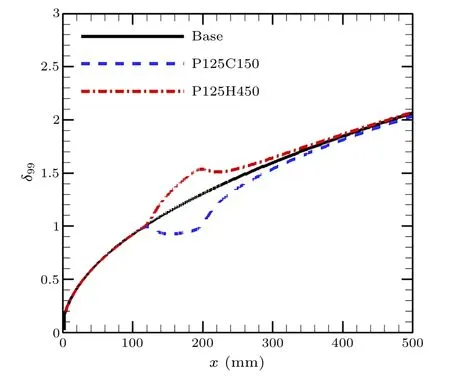
Figure 5 shows the growth rates under three different conditions.The figure only illustrates two-dimensional unstable waves(β=0).Cooling shifts the neutral curve to higher frequencies,the range of unstable frequencies becomes narrower,and the neutral curve becomes locally flat.These effects are related to the change in the local boundary layer thickness.Cooling reduces the thickness of the boundary layer, so the frequency range of the unstable waves becomes narrower.At the same time, the wavelength of the most unstable wave decreases and the frequency of the unstable waves increases.For local heating,Fig.5(c)indicates that the range of unstable frequencies is locally broadened.This can also be explained by the change in the boundary layer thickness.Figure 5 shows that local cooling/heating will stabilize/destabilize the first mode and destabilize/stabilize the second mode,which is consistent with the previous conclusions for a uniform wall temperature distribution.By comparing the trends of pressure gradient and maximum growth rate, Fedorovet al.[24]found that the second mode is mainly affected by the pressure gradient, while the wall temperature has little effect.However,the changes to the neutral curve show that the first or second mode is directly influenced by the wall temperature,while the pressure gradient only influences the maximum growth rate.

Traditional LST neglects the presence of non-parallelism,which will be significant in the flow field when the wall temperature changes.In order to account for this, we use LST that incorporates non-parallelism,which has been extensively described by Huang and Wu.[29]Figure 6 presents a comparison of the growth rates and amplitudes obtained using the two LST methods.As shown in Fig.6(a),the growth rates obtained by both LST methods are in broad agreement.The impact of non-parallelism is mainly concentrated near the wall temperature jump location, where the traditional LST would yield a smaller growth rate.Figure 6(b) indicates that the amplitude evolution curves obtained from the two LST methods almost coincide, suggesting that non-parallelism has minimal influence on the stability analysis results in the working conditions discussed in this paper.Therefore, we employ the traditional LST for subsequent calculations in this study.

3.2.Direct numerical simulations

3.2.1.Single frequency disturbance evolution

In a hypersonic boundary layer, the growth rate of the second mode is much larger than that of the first mode.Moreover, for the second mode, the two-dimensional waves are more unstable, so we only perform two-dimensional numerical simulations for the second mode.The disturbance evolution is simulated for two frequencies 180 kHz and 330 kHz,with 180 kHz being the downstream dominant disturbance frequency and 330 kHz crossing the locally elevated section of the neutral curve.In addition, when performing DNS for the evolution of a single-frequency disturbance, the grid should vary according to the wavelength of the selected wave, i.e.,λ180kHz≈4.0 mm,λ330kHz≈2.2 mm.According to our experience,approximately 50 points within a wave are sufficient.For the 180 kHz and 330 kHz waves,the calculations are performed on 11000×400 and 6200×400 grids, respectively.After obtaining the base flow, the initial disturbance is set atx=50 mm,far from the head in order that both frequencies are stable.The initial disturbance obtained from the LST is added at the entrance, as shown in Fig.7.The initial amplitude is 10-6to ensure that the growth of the disturbance is always in the linear stage.

Figure 8 shows the velocity eigenfunctions of the unstable waves atf=180 kHz,wherex=155 mm is located at the core section of the wall temperature change andx=200 mm is located at the end of the wall temperature change.The DNS and LST results match well, which demonstrates the reliability of our program.As can be seen in Figs.8(a) and 8(b),local cooling shifts the first peak of the velocity eigenfunction toward the outer edge of the boundary layer,which means that the disturbance amplitude becomes smaller, close to the wall.Figure 8(c)indicates that local heating makes the eigenfunction shape fuller and another peak appears near the wall.The disturbance energy is more uniformly distributed within the whole boundary layer,and this shape change gradually recovers at the end of the wall heating zone.These changes are clearly caused by the wall temperature, which again confirms that modifying the wall temperature directly affects the second-mode stability characteristics.

Figure 9 shows the evolution of the time-averaged disturbance kinetic energy forf=180 kHz andf=330 kHz.The time-averaged disturbance kinetic energy is calculated by

For the unstable wave atf=180 kHz, P125C150 suppresses the growth of the unstable wave, whereas P125H150 promotes the growth of the unstable wave in the region of modified wall temperature, as shown in Figs.9(a) and 9(b).For the unstable wave atf=330 kHz, both P125C150 and P125H450 experience greater disturbance amplitudes than in the base case across the section where the wall temperature changes.The high-frequency wave experiences stronger attenuation downstream of the cooling, as shown in Fig.9(b).Therefore, changing the local wall temperature has different effects on unstable waves of different frequencies.Local cooling stabilizes the low-frequency unstable wave and further destabilizes the high-frequency unstable wave.Local heating amplifies both high-and low-frequency unstable waves locally.

3.2.2.Broadband disturbance evolution

DNS of a single-frequency disturbance was performed as stated in the above subsection.During the actual transition process,however,the flow naturally“selects”frequencyspecific disturbances from the free flow disturbances as the nose goes through the receptivity stage.

Moreover,the transition process is affected by a combination of multiple-frequency unstable waves,and there is a mutual transfer of energy between different frequencies.Thus,it is not enough to simulate only a single-frequency disturbance.In this subsection, we present the DNS results for broadband frequency disturbances by adding random disturbances at the entrance.As a result,these simulations are closer to the natural transition process.

For theMa=6 sharp cone boundary layer, many experiments have confirmed that the transition is dominated by the second mode.[7]Taking into account the computation time,we only perform two-dimensional numerical simulations.Under the current flow conditions,most of the unstable wave frequencies are concentrated at 150–350 kHz.Hence, the calculations are conducted on a 12680×400 grid.For P125C150 and P125H450,the wall temperature change starts atx=125 mm,and the baseflow before that is exactly the same,so there is no need to focus on the receptivity phase of the nose.After obtaining the baseflow, the new computational domain is taken asx=50–500 mm.The random disturbances added at the entrance is as follows:

whereA0is the initial disturbance amplitude.The range of the disturbances added in these simulations is from 50.4 mm ≤x≤50.8 mm.Hader and Fasel[30]have shown that such random disturbances can effectively simulate the natural transition process.It is important to notice that, when introducing noise in the simulation, the level has been adjusted to find the experimental pressure instability amplitude.The initial amplitude isA0=0.01, frequency interval is ∆f=1.3 kHz,and sampling time isTsampling=1.5 ms.Forf=150 kHz unstable waves, the sampling time contains about 220 periods.Figure 10 compares the pressure pulsation spectra obtained from DNS with the experimental results, wherefIIis the second-mode peak frequency.The disturbance amplitude and the second-mode peak position of DNS are in good agreement with the experimental data.Figure 11 shows the disturbance field of pressure and temperature, indicating a distinct“rope-like” structure, which is a characteristic of the second mode.

Figure 12 shows the amplitude evolution of the disturbance kinetic energy.Compared with the base case,both cooling or heating produce an initial increase in amplitude when the wall temperature starts to change,whereas the reasons for this are different.As can be seen in Fig.10, atx=150 mm,the peak of P125C150 moves to higher frequencies compared with the base case, whereas the peak of P125H450 does not change significantly but the spectrum becomes flatter.Combined with the neutral curve in Fig.5,we conclude that this is because the local cooling destabilizes the high-frequency disturbance, and the neutral curve becomes flatter locally.This lengthens the integral path of the high-frequency disturbance and eventually leads to an increase in the disturbance amplitude.Local heating makes the frequency range of the unstable wave larger and the integral path of the disturbance longer,which also eventually leads to an increase in the disturbance amplitude.

After the end of the wall temperature change, the disturbance amplitude of P125C150 decreases before rapidly increasing, while the disturbance amplitude of P125H450 continues to increase.At this time, for local cooling, the lowfrequency disturbance has not yet increased sufficiently, and the amplitude is small, so the disturbance kinetic energy amplitude briefly decreases.At the end of the model,P125H450 has the largest amplitude, while P125C150 has the smallest amplitude.Referring to the relevant experimental results,[31]the transition may not have occurred within the finite length of 500 mm under the current conditions.However,a comparison of the amplitudes shows that local cooling has an inhibitory effect on the transition and local heating has a facilitating effect on the transition,which is consistent with the experimental results of Fedorovet al.[24]

In the downstream region,the disturbance growth rate of P125C150 is significantly larger than that of the base case,while the disturbance growth rate of P125H450 is significantly smaller than that of the base case (Fig.12).Figures 3 and 5 indicate that,although local cooling produces a smaller boundary layer thickness downstream,the unstable waves in the neutral curve have a larger frequency range, and the disturbance has a larger growth rate.This is contrary to the findings Fedorov ofet al., which suggested that local cooling results in a smaller boundary layer thickness and a smaller frequency range of unstable waves,leading to a shorter disturbance integral path and a delayed transition.However, our results indicate that local cooling only causes a transition delay because it locally suppresses the growth of low-frequency disturbances that will dominate the transition downstream.Moreover, local cooling promotes the local high-frequency disturbance instability and makes the downstream flow more unstable.For local heating, as shown in Fig.6, it is observed that, while both high and low frequency unstable waves are amplified locally,the unstable wave’s frequency range and growth rate decrease downstream of the heating endpoint compared to the base case.Local cooling or heating has different effects on unstable waves with different frequencies.The wall temperature changing section and its downstream also have different effects on transition, which may be the reason why the local wall temperature is very sensitive to the location.

Figure 13 shows theN-factor envelope.Given the importance of the attenuation section,the starting point of the integral is selected as 50 mm.For the base case,the amplitude ofis enlarged by about 58 times in the range 100–500 mm,that is,the increment of theN-factor obtained by DNS is about 4.1; this is comparable well with the factor of 4.3 within this length range given by LST.By comparing Figs.12 and 13,the two trends and the quantitative results are roughly the same.This suggests that the effect of local wall temperature on the transition could be studied using theN-factor envelope.

3.3.Effect of temperature and action position on transition

To achieve LFC using the local wall temperature,the effect of the local wall temperature on the transition is now investigated using the eNmethod.We vary the local wall temperature and heating/cooling position according to the specific parameter settings listed in Table 1.

According to the LST and DNS results, we focus on the unstable waves within the rangef=120–500 kHz,and the integral starting position of the disturbance is 50 mm.Figure 14 shows theN-factor obtained by changing the local cooling position.Local cooling causes an additional peak in theN-factor envelope.Compared with the base case, upstream cooling leads to a decrease in theN-factor and downstream cooling leads to an increase in theN-factor.The farther the cooling position is upstream, the less theN-factor decreases.TheNfactors forf=178 kHz andf=204 kHz are compared in Figs.14(a) and 14(b).When the cooling location is only a short distance upstream, the attenuation effect of cooling on low-frequency unstable waves is stronger.

Figure 15 illustrates a comparison of theN-factor for three different frequencies of unstable waves at various heating positions.Among these frequencies,f=178 kHz represents the most unstable second mode frequency downstream in the base case.The heating positions of P325H450 and P425H450 are located near the end of the model,whereas the heating positions of P125H450 and P200H450 are closer to the neutral point of those three frequencies.In the case of P325H450 and P425H450,it is evident that theN-factor peaks of the three frequencies are higher compared to the base.For P125H450 and P200H450,as shown in Figs.15(b)and 15(c),it can be observed that the unstable waves atf=178 kHz andf=190 kHz experience accelerated growth in the heating section, but their growth rates decrease significantly after leaving the heating section when compared to the Base.Heating slightly downstream from the neutral point(P200H450)yields lowerN-factor peak for the unstable waves atf=178 kHz andf=190 kHz in comparison to the base case.This finding aligns with the study of Zhaoet al.,[26]which focused on the most unstable second mode in the base case and found that heating beyond the neutral point downstream suppresses the growth of this unstable wave.However, upon examining P125H450 and P200H450 in Fig.15(a), it is evident that the lower frequency unstable wave atf=165 kHz,although displaying a slightly lower growth rate than the base case downstream, undergoes a significant surge in growth within the heated section.This results in a higherN-factor of the unstable wave at that frequency compared to the corresponding value in the base case at the end of the model.Notably, P200H450 show a transition in the frequency of the most unstable wave from 178 kHz to 165 kHz compared to the base.

In essence, while heating slightly closer to the downstream can impede the growth of previously dominant unstable waves,it also promotes the growth of lower frequency unstable waves and can even induce a shift in the frequency of the most unstable waves downstream.To comprehensively account for these combined effects, we calculate theN-factor envelopes for different heating positions, as depicted in Figs.16(a)–16(d).It can be seen that theN-factor for local heating is always slightly greater than in the base case,regardless of how the position changes.Moreover,compared with local cooling,the effect of local heating on theN-factor is concentrated near the section in which the wall temperature is changed,with little effect downstream.

Figure 16 shows theN-factors obtained by changing the wall temperature at a fixed position.Figures 16(a) and 16(b)show the effects of cooling and heating, respectively.As can be seen from Fig.16(a), a stronger degree of cooling produces a more pronounced decrease in theN-factor envelope downstream.However, after the cooling exceeds a certain degree, as shown in P125C50, the growth rate of the lowfrequency waves will be larger after leaving the cooling section,although the attenuation effect of low-frequency unstable waves is stronger locally.This eventually leads to a rapid increase in theN-factor,exceeding that of the base case.In addition,excessive cooling will make high-frequency disturbances seriously unstable, leading to largeN-value peaks appearing locally,which may accelerate the onset of transition.For local heating,as shown in Fig.16(b),theN-factor is always slightly larger than that of the base case, regardless of changes in the heating temperature.The above results show that appropriate upstream local cooling can delay the transition,but excessive cooling may lead to a faster onset of transition, while local heating always slightly promotes the transition.

4.Conclusion

In summary, we have investigated the effects of local wall temperature on the stability and transition of a hypersonic boundary layer using DNS and the eNmethod based on LST.It is found that the local wall temperature significantly affects the neutral curve and the stability of the boundary layer.The results of single-frequency disturbance DNS show that local wall temperature has different effects on unstable waves of different frequencies.Local cooling stabilizes low-frequency unstable waves and amplifies high-frequency unstable waves,whereas local heating amplifies all unstable waves locally at the same time.The disturbance amplitude and the secondmode peak frequency obtained by the broadband disturbance DNS are in good agreement with the experimental results reported in literature.Neutral curves and DNS results suggest that local cooling/heating has a dual effect on the stability of the hypersonic boundary layer.Although local cooling locally inhibits the growth of the low frequency waves that will dominate the transition downstream,it also makes the downstream flow more unstable,which is contrary to the conjecture of Fedorovet al.Local heating amplifies the unstable waves of all frequencies locally, but it makes the downstream flow more stable.Therefore, to accurately evaluate the effect of local wall temperature on transition, both positive and negative effects should be considered, and a comprehensive assessment should be conducted.

The amplitude of the disturbance kinetic energy is found to have the same trend as theN-factor envelope.Thus, theN-factor envelope is used to study the effect of the local wall temperature on the transition.The results show that local cooling upstream can delay the onset of transition.However, excessive cooling may accelerate the onset of transition for two specific reasons: (i) Excessive cooling will make the highfrequency waves seriously unstable,resulting in additionalNfactor peaks.(ii)Excessive cooling makes the low-frequency disturbance seriously unstable downstream, whereupon the disturbance amplitude increases rapidly and exceeds that of the base case.Local heating always weakly promotes the transition, and the effect on theN-factor is concentrated in the section where the wall temperature changes, with little effect downstream.Combined with existing conclusions,we recommend the careful use of local cooling to delay the transition in practical situations.If the transition has already occurred upstream, cooling upstream may further advance the transition.If the local cooling is guaranteed to be located upstream of the original transition onset, further destabilization of the highfrequency disturbance caused by the cooling may accelerate the onset of transition.A more secure approach is appropriate for cooling upstream of the original transition onset point.

Acknowledgment

This work was supported the National Natural Science Foundation of China(Grant No.92271102).