Synchronization of second-order Kuramoto networks from the perspective of edge dynamics

Liang Wu·Jiuming Zhong·Haoyong Chen

Abstract This paper presents new synchronization conditions for second-order phase-coupled Kuramoto oscillators in terms of edge dynamics.Two types of network-underlying graphs are studied,the positively weighted and signed graphs,respectively.We apply an edge Laplacian matrix for a positively weighted network to represent the edge connections.The properties of the edge Laplacian matrix are analyzed and incorporated into the proposed conditions.These conditions take account of the dynamics of edge-connected oscillators instead of all oscillator pairs in conventional studies.For a network with positive and negative weights,we represent the network by its spanning tree dynamics,and derive conditions to evaluate the synchronization state of this network.These conditions show that if all edge weights in the spanning tree are positive,and the tree-induced dynamics are in a dominant position over the negative edge dynamics, then this network achieves synchronization.The theoretical findings are validated by numerical examples.

Keywords Kuramoto oscillator·Signed graph·Synchronization·Edge Laplacian matrix·Spanning tree

1 Introduction

The synchronization phenomenon exists in many networked systems across various disciplines.Such a phenomenon occurs when a group of interacting oscillators evolve towards a common target.Among various synchronization patterns,the second-order Kuramoto model has been adopted to provide theoretical insights into the slow synchronization phenomenon observed in certain types of natural and engineering networks, such as special kinds of fireflies [1],Josephson junctions[2],and power grids[3–7].In this type of network,each Kuramoto oscillator is capable of adapting its own frequency, which might prevent the network from being synchronized.

In general,the synchronization among the phase-coupled Kuramoto oscillators is a result of three interplaying elements, which are the unique dynamics of Kuramoto oscillators,their initial states,and the connection pattern among them.With the consideration of these factors, a great deal of progress has been made to identify synchronization conditions for the second-order Kuramoto network in recent years[8].It is shown that if the coupling strength is strong enough to dominate the non-uniformity of the oscillators’parameters,or/and the oscillators stay close enough to each other,then this network achieves frequency synchronization while the phase differences remain cohesive.In particular, graph theory and control theory provide indispensable analysis methods for deriving quantifiable synchronization conditions.Contraction analysis methods have been used in[3,4,6,9,10]to derive sufficient conditions for a network,whose underlying graph diameter is not greater than two.For a general network topology,energy/Lyapunov functions have been constructed in [4–7, 11] to provide synchronization conditions.In general,contraction-typed conditions are less conservative than energy-function-based conditions.However, they are not applicable to networks with general connectivity.On the other hand,the energy function method has gained increasing attention due to its flexibility in characterizing topology-related synchronization conditions for the second-order Kuramoto network.

As far as we know,a majority of synchronization conditions were developed via the complete-graph-based energy function methods.These conditions connect the given-graphinduced with the complete-graph-induced phase differences of oscillators by using the graph algebraic connectivity [5,6,11],the lengths of graph paths[11],or the diameter of a graph complement[4,7].Therefore,a natural question to ask is if there exists a way to construct an energy function using only phase differences from edge-connected oscillators.This question was partly answered in the multi-agent consensus research community during recent years[12–14],where the edge dynamics were considered instead of node dynamics.The consensus over edges is referred to as the edge consensus or the edge agreements.A similar methodology was adopted in[15,16]to provide synchronization conditions for the firstorder Kuramoto network.However, the synchronization of the second-order system from the viewpoint of edge dynamics is worth further investigation.

Besides, a large number of developed synchronization conditions in the aforementioned literature are only applicable to the scenario of positive edge weights.Negative couplings among Kuramoto oscillators have been discovered in social networks and neurons [17, 18].For a power system model,the graph edges represent the transmission lines connecting generators and loads,while the edge weights are the power transmitting capacities [3–5].The edge weights of a power system are supposed to be positive,but they can turn negative when the corresponding transmission lines are capacitive[19],which brings impact on the system stability.Local stability around the synchronized states of a Kuramoto network with negative weights has been studied in[20].Nevertheless,it remains unclear if a signed network can achieve synchronization when oscillators are scattered far from each other,especially in the case of second-order dynamics.

Inspired by the aforementioned works,this paper applies the state-of-the-art graph techniques to investigate the synchronization of a second-order Kuramoto network on an undirected graph,where the edge weights are allowed to be both positive and negative, i.e., a signed graph.By appropriately designing energy functions,we derive sufficient and explicit conditions to achieve phase cohesiveness for edgeconnected oscillators; and the frequency synchronization among them.The main contributions of this work are mainly twofold.First,for graphs with only positive edge weights,we introduce a new definition of edge Laplacian matrix, based on which we construct a novel edge-induced energy function.A useful relation is proposed to connect the minimum positive eigenvalue of the edge Laplacian matrix with the graph algebraic connectivity, which is essential in deriving synchronization conditions from the proposed energy function.Second, we extend our studies to signed graphs.To derive synchronization conditions for this type of network,we construct an energy function using the information of oscillators’relative angles induced by a spanning tree.We show that when the edge weights of the spanning tree are positively great enough against the negative weights, synchronization is achieved among the oscillators.Numerical examples are given to verify the effectiveness of the presented conditions.

Notation Let‖·‖and‖·‖∞be the Euclidean and infinity norm,respectively.For symmetric real matricesXandY,means thatX-Yis positive(non-negative)definite.For a symmetric real matrixX,we denote its minimal and maximal eigenvalues asλ(X) andλ(X), respectively.Letσ(X)be the maximal singular value of a matrixX.IfXis a set,then denote|X|as its cardinality.LetIn(On)and 1n(0n)be an identity(null)matrix and a all-one(all-zero)column vector with the dimensionn×nandn×1,respectively.Define a function as sinc(x):=sin(x)/x.

2 Preliminaries

A connected and undirected graph is defined byG:=(N,E,W)consisting of a node(vertex)setN,an edge setE⊆N×N,and an edge weight matrixW:=diag{ai j} ∈R|E|×|E|for all(i,j) ∈E.The edge weightsai jsatisfyai j=a ji/= 0 iff(i,j) ∈E, otherwise,ai j= 0.Here,the weightsai jfor(i,j) ∈Ecan be positive or negative,which represents a signed graph.By associating an arbitrary orientation to the edges,the incidence matrix ofGis denoted byB∈R|N|×|E| with elementsbik= 1 if the nodeiis the source of thekth edge,bik= -1 ifiis the sink of thekth edge,andbik=0 otherwise.

Next,consider a set of second-order Kuramoto oscillators defined on the graphG,whose dynamics are given by

whereθi,diandpiare the phase, damping coefficient and naturalfrequencyoftheithoscillator,respectively,andθi j:=θi-θ j.Here,di>0 andpiare constants.Letϑ:=BTθ∈R|E|×1 be a vector of collecting all the edge-induced phase differences of the Kuramoto oscillators, and defineM:=diag{mi} ∈R|N|×|N|,D:= diag{di} ∈R|N|×|N|,p=[p1,...,p|N|]T∈R|N|×1,andΠ(ϑ) := diag{sinc(θi j)} ∈R|E|×|E|for(i,j) ∈E.Then,we can rewrite the Kuramoto system(1)as the following vector form:

Without loss of generality, throughout this paper, we assume that the sum of natural frequencies of all Kuramoto oscillators is zero,i.e.,1T|N|p= 0.In addition,we consider that all oscillators are evolving in the Euclidean space instead of ann-torus.The above two points are commonly taken when the Kuramoto system is studied from the viewpoints of control theory and engineering application[3,5,10].Next,we provide the following definitions for the dynamics of the Kuramoto network(2).

Definition 1 The Kuramoto network (2) is said to be edge cohesive if the phase differences between edge-connected oscillators satisfy|θi j(t)|≤ηfort≥0 and for all(i,j)∈E,whereη∈[0,π).

Definition 2 The Kuramoto network (2) is said to achieve frequency synchronization if the frequencies of oscillators satisfy

Definition 1 is also termed phase cohesiveness in some studies[6,9],which can be achieved when the network’s initial configurations satisfy some sufficient conditions.These conditions were derived by taking into account the dynamics of phase differences among all oscillators, which may increase the conservativeness in the cohesive conditions.Following a similar terminology used in the multi-agent consensus research community [12–14], edge cohesiveness is definedheretohighlightthattheaimofthisworkistodevelop conditions in achieving a certain level of boundedness for oscillators with physical connections.Towards this end,the following lemma is introduced to show that edge cohesiveness implies frequency synchronization.

Lemma 1If the Kuramoto network(2)is edge cohesive,then it achieves frequency synchronization.

ProofThe proof of Lemma 1 is based on the application of LaSalle’s invariance principle[21].Since the edge cohesiveness is defined in terms of phase difference variables, the first step is to construct a Lyapunov-like function consisting ofθi j,whose time derivative is non-positive.To this end,we denote byBc∈R|N|×|Ec|the incidence matrix of a complete graphGc=(N,Ec),and modify the energy function used in[22,Chapter 5]with respect to the trajectory(BTc θ, ˙θ)of the Kuramoto system(2)as follows:

To apply LaSalle’s invariance principle,we need to show that there exists a compact positively invariant set (PIS)denoted byDfor the system(2)with respect to the trajectory(BTc θ, ˙θ).A set is said to be a PIS if the initial states of a system are located in this set,then the trajectories will remain in the set[21].As shown in[7,Lemma 3.3],the frequencies of Kuramoto oscillators ˙θiare bounded by

whereδi jare positive constants satisfyingδi j≥η.Therefore, the PISDfor system (2) can be defined by (4) and(5) asD:= {(BTc θ, ˙θ) ∈ R(|Ec|+|N|)×1| ‖BTc θ‖∞≤max(i,j)∈Ec δi j,‖˙θ‖∞≤maxi∈N ci},which is compact.

Obviously,the energy functionUis continuously differentiable inD,whose derivative is computed as

The matrixBcMcBTcin (6) can be viewed as a Laplacian matrix for a complete graph with the edge weights beingai j=mim jfor(i,j)∈Ec,then it holds that

Using(2)to replace ¨θin the first term in the right-hand-side of(6)and applying(7),we have

Similarly,for the second term in the right-hand-side of(6),we have

where the last equality holds due top=0 andB=0.By applying(8)and(9)to(6),one has ˙U=-ms˙θTD˙θ≤0.LetE:={(BTc θ, ˙θ)∈D|˙U(Bcθ, ˙θ)=0}={(BTc θ, ˙θ)∈D|˙θ=0|N|}andMbethelargestinvariantsetinE.Then,by LaSalle’s invariance principle[21],above arguments suffice to conclude that all trajectories(BTc θ, ˙θ)starting inDconverges toMast→+∞,which indicates the achievement of frequency synchronization.This completes the proof.■Remark 1As shown in [22, Chapter 5], a power system model taking the form of (2) on an undirected graph does not exist any complicated behaviors such as limit cycles or chaotic motions.The boundedness of every single oscillator’s phase results in the convergence of the system trajectory to an equilibrium point (frequency synchronization).Via Lemma 1, we show that such boundedness can be defined in terms of the phase differences of edge-connected oscillators,which guarantees frequency synchronization.

3 Edge-based synchronization conditions for networks with positive edges

Based on the application of an edge Laplacian matrix,this section presents synchronization conditions for the Kuramoto network (2) with all edges being positively weighted,which is stated in the following assumption.

Assumption 1 AssumetheunderlyinggraphfortheKuramoto network(2)is connected,and all its edge weights are positive.

Proposition 1If the phase differences of the Kuramoto oscillators satisfy|θi j| ≤η for all(i.j) ∈E,then the following relation holds:

ProofThe proof is based on three observations as follows.First, all eigenvalues of a Laplacian matrix with positive edge weights for a connected graph are positive except one being zero.For the Kuramoto network(2),consider a statedependent Laplacian matrix asL(G(ϑ)) :=BWΠ(ϑ)BT.Since |θi j| ≤ηfor all(i.j) ∈E, we have sinc(θi j)>0, which implies thatΠ(ϑ) is positive definite.Then, it holds that 0 =λ1(L(G(ϑ)))<λ2(L(G(ϑ))) ≤··· ≤λ|N|(L(G(ϑ))).

whereξ∈R|N|×1is the eigenvector with respect to the zero eigenvalue of～L(G(ϑ)).Note thatξis also the eigenvector of～L(G)corresponding to the eigenvalue of zero.

Finally,for the real and symmetric matrix～L(G(ϑ)),there exists an orthogonal matrixPsuch thatPT～L(G(ϑ))P=Λ:=diag{0,λ2(～L(G(ϑ))),...,λ|N|(～L(G(ϑ))}.Then,one has that

where the last inequality holds due toΛOandΛλ2～L(G(ϑ))I|N| = diag{0,0,λ3(～L(G(ϑ)) -λ2(～L(G(ϑ)),x···,λ|N|(～L(G(ϑ)) -λ2(～L(G(ϑ))}O.(12) indicates that

where(11)is applied.This completes the proof.■

Remark 2A relation similar to (10) can be found in [16].Compared to that of[16],our result is less conservative and is explicitly connected to the graph algebraic connectivityλ2(～L(G))of a scaled graph.

Remark 3For directed graphs, (10) can be extended to the cases of a directed spanning tree and a directed cycle.By using the properties of the Laplacian matrices for these two types of digraphs from [24, Proposition 1], this can be achieved with a slight modification of the arguments in the proof of Proposition 1.However, (10) does not hold for a general digraph.The main challenge lies in the fact that the directed edge Laplacian matrix after symmetrization is not generally positive semi-definite.This remains further exploration.

To fulfill the conditions of Lemma 1, one can identify a positively invariant set for a Kuramoto network by using a non-negative energy function as in [4, 5, 7, 10].From the perspective of edge dynamics, we definex:= [ϑT˙θT]T∈R|E∪N|×1, and construct the following edge-based energy function to analyze the dynamics of the Kuramoto network(2):

whereαis a constant that will be in the following lemma.

Lemma 2Define the following two|E∪N|×|E∪N|matrices:

ProofThe energy function (14) can be written asV(x) =xTH(ϑ)xwith

Theorem 2Under Assumption 1,if the following conditions are satisfied,

ProofUsingΠ(ϑ/2)ϑ/2 = sin(ϑ/2), the energy function(14)can be rewritten as the following form:

Then,the derivative of energy function(20)along the trajectory of the Kuramoto system(2)is

whereΨ(ϑ) := diag{cos(θi j)} ∈R|E|×|E|for all(i,j) ∈E.After some mathematical manipulations, from (21), we obtain

Some estimations related to ˙Vare given as follows:

and

Then,applying(23),(24)and(10)to the corresponding terms in(22),we have

which gives the following relation:

As(19)is satisfied,(27)and the second inequality of(15)imply that the following relation,which holds fort≥0,

(28) indicates that the Kuramoto network (2) is edge cohesive.Then, by Lemma 1, we conclude that network (2)achieves frequency synchronization.This completes the proof.■

Remark 4The condition (19) defines a positively invariant set for the Kuramoto network(2)such that its phase differences remain edge cohesive over time.This set is explicitly related to the network information such as the parameters,the initial states of each pair of physically connected oscillators,and the underlying network topology.This information determines the edge dynamics of coupled oscillators.The disadvantage of (19) is that it can not deal with the case of the signed graph,which will be tackled in the next section.

4 Spanning-tree-based synchronization conditions for networks on signed graphs

This section presents synchronization conditions for the Kuramoto network(2)on a signed graph from the perspective of a spanning tree.A connected graphGhas at least one spanning treeGT:=(N,ET,WT), which is a sub-graph ofGwith all the nodes connected by|ET|=|N|-1 edges inE.A co-treeGC:=(NC,EC,WC)contains the remaining edges ofGthat are not included in the spanning tree,i.e.,EC:=EETand|EC|=|E|-|N|+1.The following assumption is given regarding a positively weighted spanning tree.

Assumption 2 Assume the underlying signed graph for the Kuramoto network(2)is connected,and there exists at least one spanning tree,where all the edge weights are positive.The above assumption is necessary for the synchronization of a network.If it does not hold,then there exists at least one cutset[20],which consists of negative edges only.In this case,the graph Laplacian matrix possesses at least one negative eigenvalue[14,20,25],which prevents the associated network from being synchronous.

Remark 5A signed graph under Assumption 2 is structurally unbalanced.Structural balance and unbalance are two important concepts in the consensus problems of networks with antagonistic interactions[26].Such interactions are defined on a Laplacian matrix denoted asLs:= [li j]withli j=ai jwhich is different from the one used in this work.The eigenvalues ofLsare always nonnegative regardless of whether a signed graph is structurally balanced or unbalanced[27],which facilitates network synchronization.Given this reason, the study of the Kuramoto network(2)onLsis beyond the scope of this paper.

Some matrices and their properties that will be used in this section are introduced as follows.

then Q(a,b)is positive definite.

where the constantαTwill be defined in the following lemma.

Lemma 3Define the following two|ET∪N|×|ET∪N|matrices

ProofNote that the first term in the energy function (31)is equivalent toϑTT RWΠ2(ϑ/2)RTϑT= 4 sinT(ϑ/2)Wsin(ϑ/2).Then,the derivative of energy function(31)along the trajectory of the Kuramoto system(29)is

After some mathematical manipulations, from (36), we obtain

If|θi j(t)|≤ηfor(i,j)∈E,we have

whereQ(sinc(η),1)is positive definite since(30)holds fora=min{sinc2(),sinc(η)}andb=1.Then,applying(38)to(37),we have

whereλ(D-αT FT)> 0 holds due to condition (34).As(34)holds,we apply(32)to(37)to derive

Following the same arguments in the proof of Theorem 2,we have that

5 Numerical studies

This section verifies the effectiveness of the proposed methods on some numerical examples.First, we compare the synchronization conditions from Theorem 2 with those from [4, 5, 7] in estimating a positively invariant set(PIS) for the Kuramoto network (2) (see Remark 4).A three-oscillator network associated with a path graph is chosen.The parameters of this network are given asp=[1.4,1.4,-2.8] × 10-4,m= [1.3263,1.2732,1.2202],d= [2.7852,2.5465,2.6844], anda12=a23= 0.1489.Numerical results are shown in Fig.1, which demonstrates thattheproposedmethodproducesagreaterregionthanthose by[4,5,7].However,this does not imply that the presented conditions are generally superior to the existing methods[4,5, 7] due to the lack of a theoretical comparison method.Given this reason,our method can be seen as a complement to the current methods.One can combine these methods to analyze a given network, and choose the best results from them.

Next, conditions from Theorems 2 and 5 are verified on a six-node network,whose topology is shown in Fig.2 with the values of edge weights.The parameters of oscillators are given as follows:p= [0.0008,0.0012,0.0004,-0.0006,-0.0013,-0.0005],m=[0.5179,0.9245,0.9669,0.8394,0.8788,0.8712],andd=[0.9912,0.9871,0.8456,0.9401,0.7426,0.8265].The initial state values of oscillators are set asθ(0) = [0.016,-0.016,0.048,-0.032,0.080,0.016],

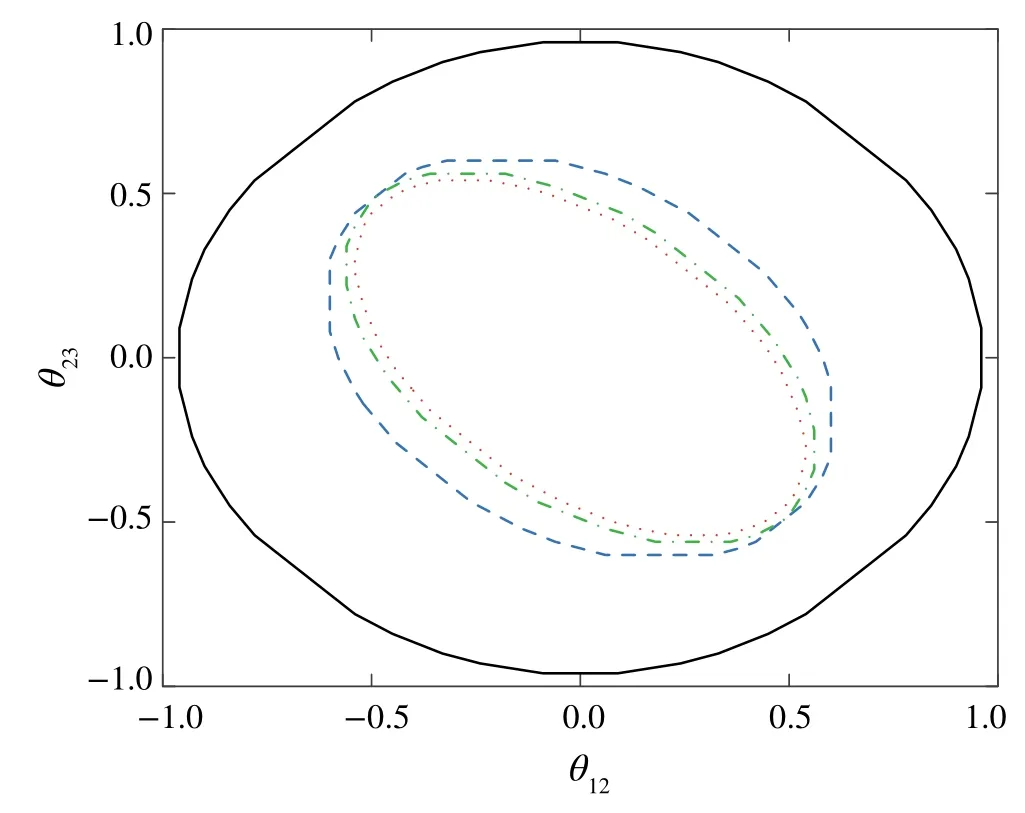
Fig.1 Comparison of PIS estimated by condition(19)(solid line)and conditions from[5](dash line),[7](dash-dot line)and[4](dot line)

Fig.2 Diagram of a six-oscillator network

Fig.3 Dynamics of BTθ(t)and ˙θ(t)of oscillators with positive edges

6 Conclusion

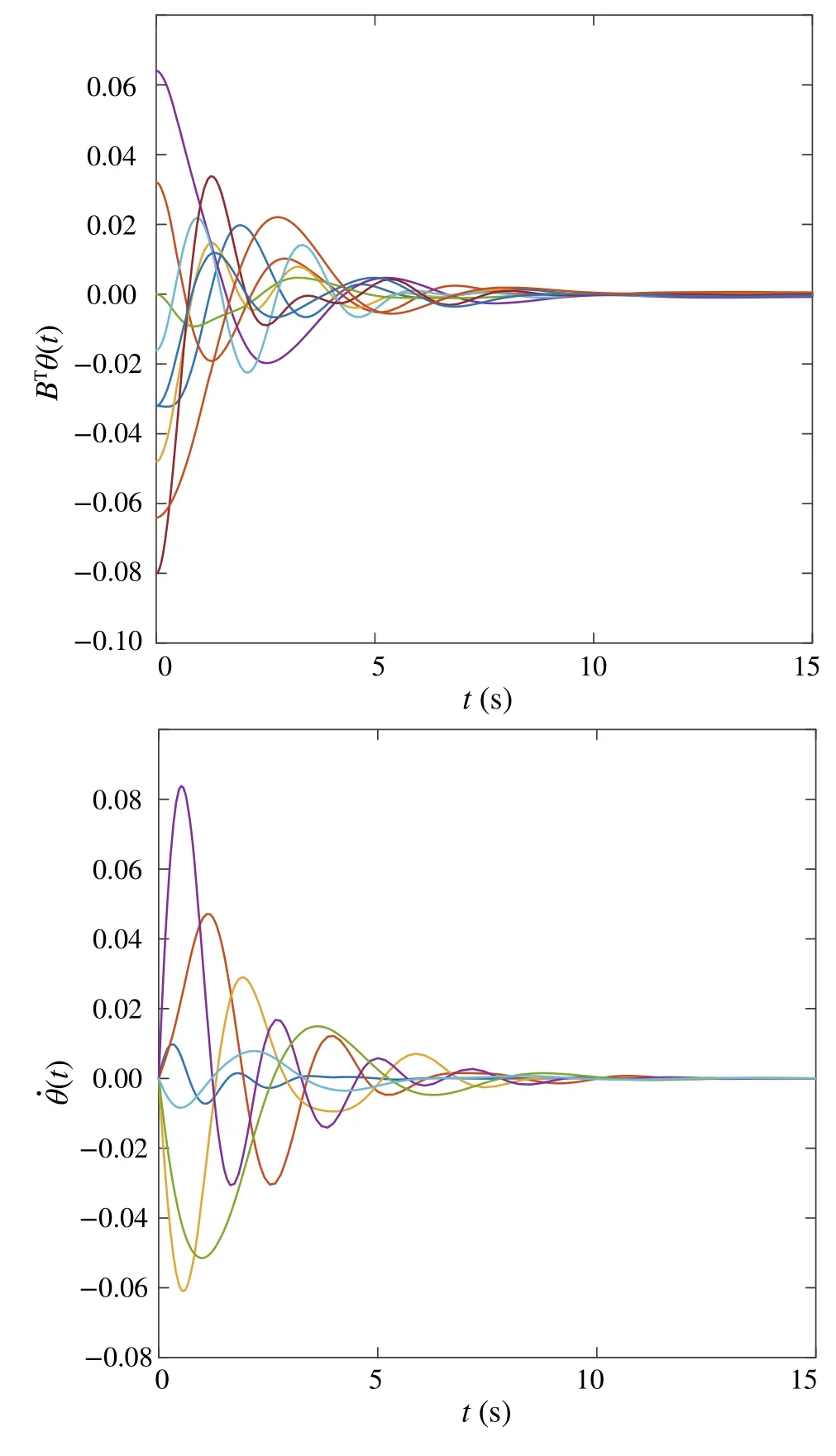
Fig.4 Dynamics of BTθ(t)and ˙θ(t)of oscillators on a signed graph

This paper investigates the synchronization of second-order Kuramoto networks from the perspective of edge dynamics instead of node dynamics.We show that the studies of the synchronization of Kuramoto networks in terms of edge dynamics have two advantages.First, compared to traditional studies, it deals with the phase cohesive problem in a more direct and natural way since it considers only the phase dynamics of physically connected oscillators.Second,the network dynamics can be mapped into the spanningtree-induced dynamics, which allows us to study network synchronization when a portion of the edges are negatively weighted.Explicit synchronization conditions are proposed by the construction of edge-based and spanning-tree-based energy functions, respectively.Numerical studies are performed to verify the effectiveness of presented conditions.Future research will focus on the extension of these conditions to the cases of directed graphs.

Acknowledgements The authors want to thank Prof.Parvaiz Ahmad Naik,Dr and Muhammad Faizan Tahir for their constructive comments that improve this work.