Consensus control of second-order stochastic discrete-time multi-agent systems without velocity transmission

Zi-Xuan Wang·Xiaofeng Zong·Ling-Jie Gai

Abstract This article studies the almost-sure and the mean-square consensus control problems of second-order stochastic discretetime multi-agent systems with multiplicative noises.First,a control law based on the absolute velocity and relative position information is designed.Second, considering the existence of multiplicative noises and nonlinear terms with Lipschitz constants,the consensus control problem is solved through the use of a degenerated Lyapunov function.Then,for the linear second-order multi-agent systems,some explicit consensus conditions are provided.Finally,two sets of numerical simulations are performed.

Keywords Consensus control·Multiplicative noises·Second-order·Discrete-time·Multi-agent system

1 Introduction

Recently, multi-agent systems (MASs) have been widely utilized in many fields, such as distributed neural network[1], formation control [2], information safety [3, 4] and so on [5, 6].MASs consist of multiple agents, each possessing autonomous and interactive capabilities, collaborating toward a shared task or objective.One of the significant advantages of MASs is their ability to adapt to changes in the environments [7].Consensus control problems are the significant branches of MASs and are widely discussed[8–11].

There are many efforts that have been reported on studying consensus control problems of first-order MASs[12–14].For instance, various studies were done for different types of consensus control problems in noisy environments.A stochastic algorithm utilizing the reducing step size was proposed to solve consensus control problems of networked agents with multiplicative noises in [15].To attenuate the effect of various noises in communication environments,Li and Zhang [16] designed a distributed stochastic control law for the first-order discrete-time MASs.Meanwhile,the impact of time delays on consensus control was also taken into account.Lin and Ren [17] solved constrained consensus problems of MASs with communication delays and unbalanced network topology graph.The exponential consensus problems of nonlinear MASs with stochastic communication delays and asynchronous switching were studied in [18].Based on Halanay-type inequality, consensus control problems of stochastic delayed MASs with time-varying topologies were studied in[19].In addition,a novel decentralizedfirst-orderalgorithmwasdesignedtosolveconsensus optimization problems in[20].However,it should be noted that the consensus problems for the second-order systems are more complicated than that for first-order systems,which also deserved attention[21–23].

Based on relative kinematic information,Liu and Liu[24]developed a distributed control algorithm to derive sufficient conditions for second-order consensus control problems of MASs with fixed communication delays.Xie and Liang[25]equated the group consensus control problems of MASs with the asymptotical stability problems of a communication delays system using the state transformation method to derive the group consensus criteria about the upper communication time-delay bound.In[26],the Lyapunov functional theory was used to provide consensus conditions for secondorder MASs with directed topologies or arbitrarily switching topologies.A second-order integrator system with uncertain bounded control input was studied to achieve coordinated tracking under a fixed-time in[27].The second-order MAS couple-group consensus problems with the influence of neighbors’ information were studied in the form of matrix inequality based on the stability theory in [28].The above studies considered noise-free environments.

In fact, the presence of various environmental noises inevitably has a significant impact on consensus control problems.Li et al.[29]designed a consensus control law based on relative position and velocity measurement information to solve the mean-square (m.s.) bounded tracking problem of MASs under additive noises and directed topologies.An average consensus control law that contained relative kinematic state information was designed for a second-order MAS with additive noises in [30].Cheng et al.[31] proposed a control law based on sampled data to achieve the average consensus of second-order MASs under additive noises and switching topologies.A consensus control law that contained relative position measurement information and absolute velocity information was proposed in[32].The above studies focused on second-order continuous-time systems with additive noises,which may not be representative of computer data or industrial production settings where discrete signals are more commonly used[33].In our previous work, Zong et al.[34] considered multiplicative noises and selected an appropriate Lyapunov function to solve the stochastic consensus control problems.Zong et al.[35]also studied consensus control problems of MASs with nonlinear terms,which contains relative kinematic information.It motivates us to study consensus control problems of discretetime MASs based on the information of absolute velocity and relative position,which are significantly meaningful and can solve the problems of consensus control in the case of missing velocity information.

This article studies consensus control problems of secondorder stochastic discrete-time MASs, where the consensus control law only depends on relative position and absolute velocityinformation.Consideringthepresenceofmultiplicative noises and nonlinear terms,consensus control problems in MASs are more complicated than those in noise-free environments.This article simplifies the nonlinear terms and solves the almost-sure (a.s.) and m.s.consensus problems utilizing a degenerate Lyapunov function.The main contributions of this article are summarized as follows:

(1) The control law is designed to solve the a.s.and m.s.consensus problems in second-order MASs with nonlinear terms,regardless of the given noise intensities and small Lipschitz constants.

(2) Explicit consensus conditions are presented for linear second-order MASs with multiplicative noises.

The rest of this article is organized as follows: Section 2 provides the basic knowledge.Section 3 simplifies the nonlinear terms and solves consensus control problems.Section 4 derives some explicit consensus control conditions for second-order linear MASs.Section 5 presents two sets of numerical simulations results.Finally, conclusions are provided.

Notation N+denotes set of positive real numbers.Define unit matrix asIN.1Ndescribes a column vector withN-dimension, where all elements are one.DefineJNas(1/N)1N1TN.ηNiis defined as aN-dimensional column vector withi-th term is one while others are 0.The Kronecker product ofBandDis described asB⊗D.Define a complete probability space(Ω,F,P).For the matrix or vectorA,its Euclidean norm is‖A‖.Eϱdenotes the mathematical expectation ofϱ.Define max{α,β} and min{α,β}, for anyα,β∈R,α∧β=min{α,β}andα∨β=max{α,β}.

2 Problem description

Considering a MAS formed byNagents, the dynamic model of this MAS(1)is described as

wherei∈N+,yi(k) ∈Rnrepresents the position measurement information of thei-agent,vi(k)∈Rndenotes the velocity information of thei-agent,ui(k)∈Rnis the control law andq(yi(k),vi(k))is the nonlinear term.

To solve consensus control problems for the MAS(1),the following control lawui(k)is proposed:

wherek1,k2are control gains,Z ji(k) is the position measurement information.Considering the existence of multiplicative noises,Z ji(k)satisfies

whereϑi j(k)denotes multiplicative noises in the communication measurement fromitojandf ji(y) denotes noises intensity function.

Assumption 2 Assume thatq(0,0)=0 and there are Lipschitz constantsμ1andμ2such that

for any givenv1,v2,y1,y2∈RN.

Assumption 3 Assume thatf ji(0) = 0 and there is a nonnegative number ¯σ jisuch that

for any giveny1,y2∈Rn,wherei∈N+,j∈N+.

Remark 1This article considers the uncertain environments modeled by multiplicative noises, and the designed control law is based on the absolute velocity and relative position information.It is different from [24, 26], where [24] uses relative position and relative delayed velocity information and[26]uses relative delayed position and absolute velocity information.

Remark 2Motivated by[26,36],we focus on the control of MASs for the failure or absence of velocity sensor in the actual environments.The lack of velocity information brings great trouble to the actual work,so we try to solve this problem by designing the control law based on absolute velocity.

Remark 3Note that multiplicative noises only affect the communication measurement.And the control law (2)designed in this article is based on the absolute velocity information,so it can be assumed that all agents accurately obtain absolute velocities.

3 Second-order MASs with nonlinear terms and multiplicative noises

Theorem 1Supposing Assumptions 1 and 3 hold,the a.s.and the m.s.consensus problems of MAS(1)are solved if k1and k2satisfy

ProofSubstituting control law (2) and state measurement value(3)into MAS(1),one obtains

where

Then,

where

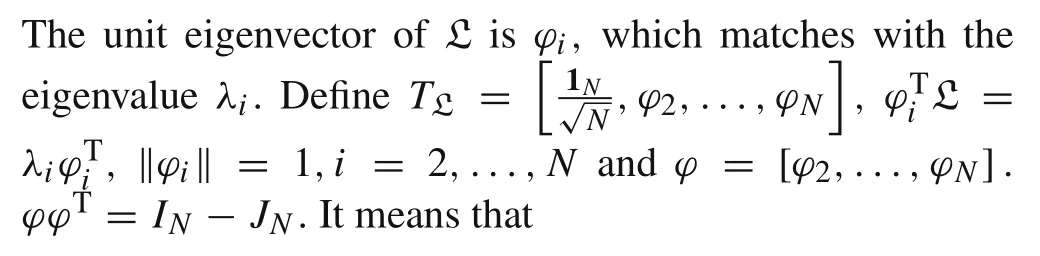
where

and

Thus,one obtains

Second,

where

Thus,one obtains

Third,

By Assumption 3,we obtain

where

Substituting(13)–(16)into(10),we obtain

The formula(19)can be rewritten as

Note that EV(s)≤2‖P‖‖¯ξ(s)‖2,then

Here,from(21),one obtains

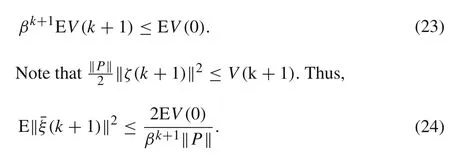
Note that all coefficients are linear growth.Thus,the m.s.exponential stability implies the a.s.exponential stability.By selecting suitableθandδsuch thatP>0 andH2<0,there exists

whereC0> 0 andγ> 0.Then,both the a.s.and the m.s.consensus problems are solved.

This proof is completed.■

Remark 4By Theorem 1,ifμ1andμ2are small enough,consensus problems of MAS(1)are solved by selectingk1andk2for any given multiplicative noise intensities.Considering the existence of nonlinear terms,we first select ak1for smallμ1andμ2suchthat2λN-k1λ2+μ1+3μ2+λ2N>0 andthen select suitablek2such that 2k2λ22-3μ1-μ2-k22λ2N>0,δ2>δ1andδ3>δ1.

4 Second-order linear MASs with multiplicative noises

Consideringq(yi(k),vi(k))=μ1yi(k)+μ2vi(k),then this consensus problem is greatly simplified.In this way, some consensus control conditions are derived as follows:

Theorem 2Supposing Assumptions1and3hold,the a.s.and the m.s.consensus problems of MAS(1)are solved if k1and k2satisfy

ProofSubstitutingq(yi(k),vi(k)) =μ1yi(k) +μ2vi(k),control law (2) and state measurement value (3) into MAS(1),one obtains

Similarly,from(23)–(24),ifP>0 andH2<0 by selecting suitableθandδthere exists(27),which means that the a.s.and the m.s.consensus problems are solved.

Then,we prove that suitableθandδcan guaranteeP>0 andH2<0.Note that

wherea11=2μ1δΛ-2k2δΛ2,a12=a21=θΛ+μ2δΛk1δΛ+μ1IN-1-k2Λ,a22=2δΛ+2μ2IN-1-2k1IN-1.

wherec11=(μ1IN-1-k2Λ)2,c12=c21=μ1μ2IN-1+μ1δΛ-k2δΛ2-μ1k1IN-1-k2μ2Λ+k1k2Λ,c22=θΛ+μ2δΛ-k1δΛ+μ2δΛ-k1δΛ+(μ2-k1)2IN-1.Thus,

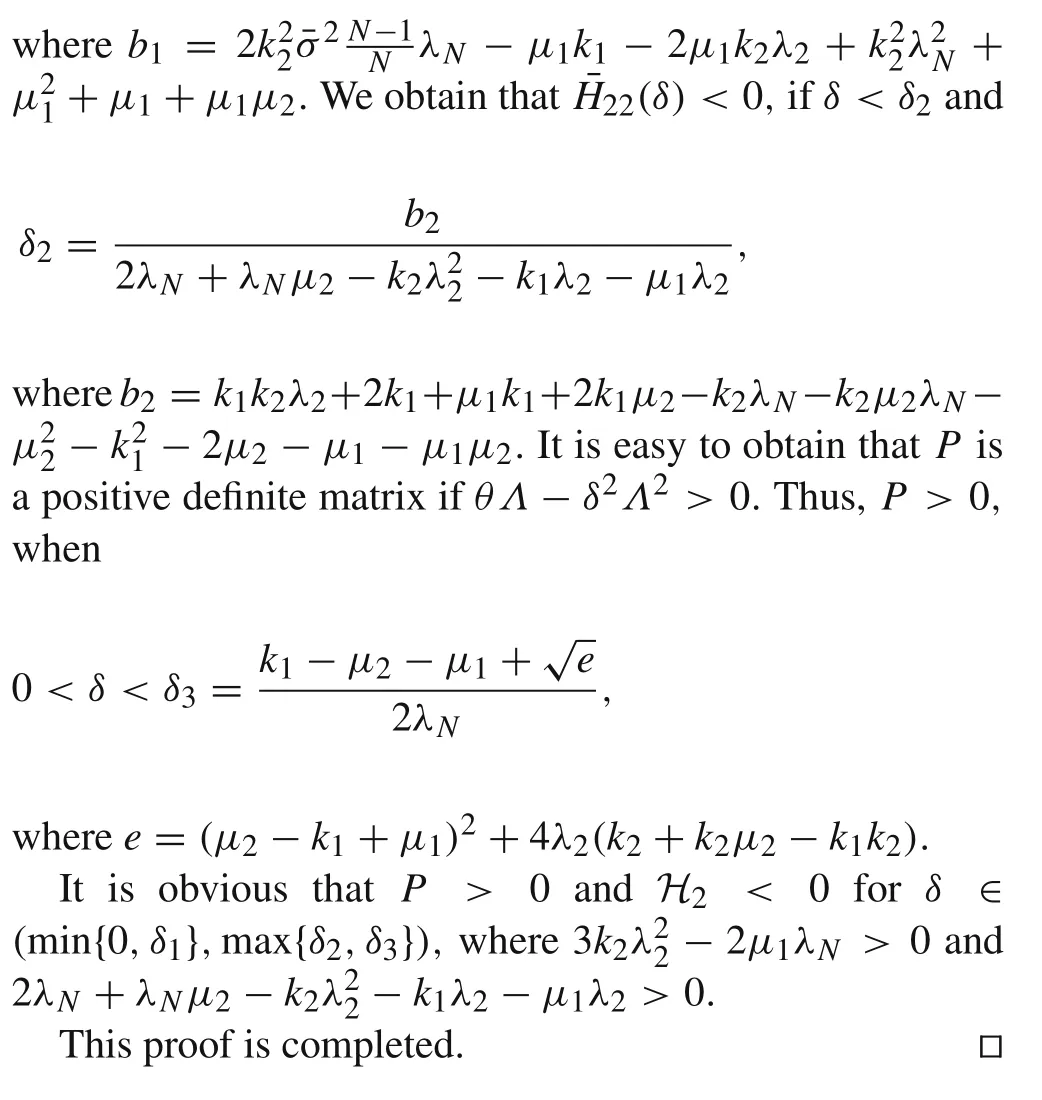
Remark 5By Theorem 2,ifμ1andμ2are small enough,consensus problems of MAS(1)are solved by selectingk1andk2for any given multiplication noise intensities.Considering the existence of nonlinear terms,we first select ak2for smallμ1andμ2such that 3k2λ22-2μ1λN>0 and then select suitablek1such that 2λN+λNμ2-k2λ22-k1λ2-μ1λ2>0,δ2>δ1andδ3>δ1.

Remark 6Section 4 studies the consensus problems of a linear MAS, but it cannot be directly degenerated from the conclusions of Sect.3.And for Sect.4, we can get more accurate consensus conclusions,which have less restrictions on control gains.

5 Simulations

Considering a MAS formed by four agents,G = {V,E,A}represents the undirected network topology graph, whereV= {1,...,4},E= {(1,2),(2,3),(3,4),(4,3),(4,2),(2,4),(3,2),(2,1)} andA=ai j∈R4×4witha12=a23 =a34=a43=a42=a24=a32=a21= 1 when the other elements being zeros.For the Laplacian matrix L of the undirected network topology graph G, its eigenvalues are as follows:λ1= 0,λ2= 1,λ3= 3 andλ4= 4.The position initial states of four agents are described asy(k) = [2,1.5,-0.9,-1.1]T.The velocity initial states of four agents are described asv(k)=[-0.8,0.8,0.4,-1.1]T.By Assumption 1, we assume multiplicative noises satisfyf ji(x) = ¯σ ji x= 1.2x, wheref ji(x) is the noise intensity function andi,j∈{1,...,4}.

5.1 Simulations of second-order MAS with nonlinear terms

To solve consensus problems, we have to choose appropriate control gainsk1,k2and Lipschitz constantsμ1,μ2,which are small enough.Assuming that the nonlinear termq(yi(k),vi(k)) =μ1cos(yi(k))+μ2sin(vi(k)).First, we choose Lipschitz constantsμ1= 0.0000002 andμ2=0.00001, thusq(yi(k),vi(k)) = 0.0000002 cos(yi(k)) +0.00001 sin(vi(k)).Note that 2k2λ22-3μ1-μ2-k22λ2N>0 and 2λN-k1λ2+μ1+3μ2+λ2N>0,we can obtain the value range of control gainsk1andk2.By choosingk1= 0.035 andk2= 0.0001, we obtainδ1= 0.0023,δ2= 0.0029 andδ3= 0.0094.Its obvious thatδ3>δ2>δ1> 0, this MAS formed by four agents can solve consensus problems by Theorem 1.

For the numerical simulations of the a.s.consensus, we have Fig.1.It is easy to observe that four agents’velocities converge to 0 almost surely and positions converge to-4.446 almost surely.

For the numerical simulations of the m.s.consensus,we get Fig.2 by taking E|yi(k)-y1(k)|2i=2,3,4and E|vi(k)-v1(k)|2i=2,3,4.It is obvious that E|yi(k)-y1(k)|2= 0 and E|vi(k)-v1(k)|2=0 such that the m.s.consensus problem of MAS(1)are solved.

5.2 Simulations of second-order MAS with linear functions

To solve consensus problems, we have to choose appropriate control gainsk1,k2and Lipschitz constantsμ1,μ2,which are small enough.First,we choose Lipschitz constantsμ1= 0.00001 andμ2= 0.0002, thusq(yi(k),vi(k)) =0.00001yi(k)+0.0002vi(k).Note that 3k2λ22-2μ1λN>0 and 2λN+λNμ2-k2λ22-k1λ2-μ1λ2>0,we can obtain the value range of control gainsk1andk2.By choosingk1=0.065 andk2=0.001,we obtainδ1=0.0116,δ2=0.0153 andδ3= 0.0192.Its obvious thatδ3>δ2>δ1> 0, this MAS formed by four agents can solve the a.s.and the m.s.consensus problems by Theorem 2.

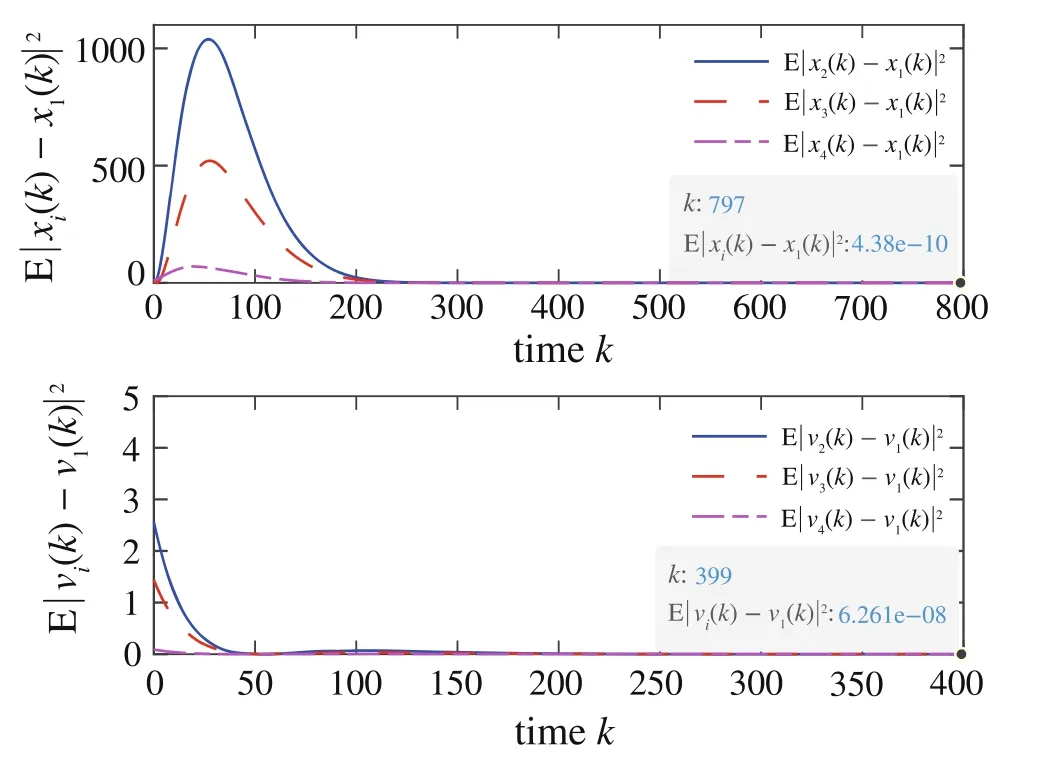
Fig.2 The m.s.consensus simulations

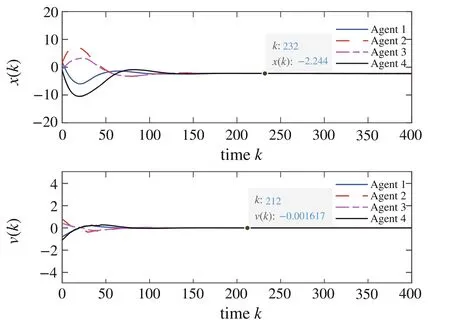
Fig.3 The a.s.consensus simulation

For the numerical simulations of the a.s.consensus, we have Fig.3.It is easy to observe that four agents’velocities converge to 0 almost surely and positions converge to-2.244 almost surely.

For the numerical simulations of the m.s.consensus,we get Fig.4 by taking E|yi(k)-y1(k)|2i=2,3,4and E|vi(k)-v1(k)|2i=2,3,4.It is obvious that E|yi(k)-y1(k)|2=0 and E|vi(k)-v1(k)|2=0 such that the m.s.consensus problem of MAS(1)are solved.

6 Conclusion

Fig.4 The m.s.consensus simulations

This article studies the a.s.and the m.s.consensus control problems of discrete-time second-order MAS with multiplicative noises and nonlinear terms.There are sometimes failure or absence of velocity sensor during the communication of the agents.Then, the velocity information cannot be obtained.Thus, the consensus control law uses absolute velocity and relative position information,which means that agents of the MAS do not need to access to other agents’velocity information.Then, the Lyapunov function theory andthestochasticstabilitytheoryareusedtosolvethea.s.and the m.s.consensus problems.The control gains are designed by some determinative conditions in terms of inequality,which explicitly show the connection between control gains and noise intensities.Finally,two sets of numerical simulations are performed.Future work will consider the formation control of discrete-time MAS with multiplicative noises and nonlinear terms based on the absolute velocity.Additionally,we aim to extend the conclusion of MASs consensus control into the smart grid control in future.

Data availability The authors declare that all data supporting the findings of this study are available.