BP 神经网络模型的电离层预报精度评估

宋秉红

( 兰州城市建设设计研究院有限公司, 兰州 730050 )

0 引言

电离层是日地空间观测环境中的一个重要组成部分，对人类生活生产产生了重要的影响. 电离层作为近地空间环境的重要组成部分，对电波通信、卫星导航定位等都有重要影响，对电离层电子总含量(total electron content，TEC)进行预报，有助于理解电离层时空演化特征和应用[1-2]. 早期学者可通过对电离层建模对电离层进行预报，主要分为经验模型(国际参考电离层(international reference ionosphere，IRI)模型)和数学模型(球谐函数模型、自回归滑动平均(autoregressive moving average model，ARMA)模型、Klobuchar 模型、整合移动平均自回归(autoregressive integrated moving average model， ARIMA)模型、NeQuick 模型等[3-4]). 近年来，人工神经网络(artificial neural network，ANN)的快速发展和计算机硬件性能的提升为电离层预报提供了新的思维方向. 深度学习方法作为一种特定类型的机器学习方法，与传统神经网络模型相比，新增了更多的网络层级和参数，在应用能力方面显著提升[5]. 人工神经网络能够处理非线性函数的问题为电离层预报提供了理论基础[6-7]. 廖文梯等[8]基于长短期记忆(long short-term memory，LSTM)神经网络模型和深度神经网络(deep neural networks, DNN)的混合模型对全球电离层TEC 进行中短期预报，该混合模型有效解决了网络层数增加带来的梯度消失的问题；马国辉等[9]基于深度学习门限循环单位(gate recurrent unit，GRU)模型对电离层TEC 进行了预报，实验结果表明：GRU 模型能够较好地预测低、中、高地区电离层TEC，且在低纬地区的精度高于中纬地区，中纬地区的精度高于高纬地区；吉长东等[10]基于LSTM 神经网络模型和总体经验模态分解(ensemble empirical mode decomposition，EEMD)结合的方法实现了对电离层TEC 值进行短期预报. 电离层TEC 数值大小与太阳活动、地磁活动、中性大气背景以及电动力学过程有关密切相关[11]，目前既有文献较多仅对TEC 数值进行时间序列分析及其预报，本文采用非线性预报反向传播神经网络(back propagation neural network，BPNN)模型将电离层格网(global ionosphere maps，GIM)数据、时间点、经纬度、太阳射电通量F10.7数据、赤道地磁活动指数Dst和全球地磁活动指数Kp数据，以此来提高电离层TEC 预报的精度，同时可为今后探索电离层数据在天气预报方面的应用提供依据.

1 原理与方法

1.1 BPNN 数学模型

BPNN 算法主要由输入层、隐含层和输出层三部分组成. BPNN 模型主要与网络层数、每层的神经元个数和激活函数有关.

神经网络模型的复杂程度取决于隐含层的个数和神经元的个数，隐含层的个数又取决于输入层和输出层的神经元个数. 随着神经元个数的增加样本训练迭代次数会随之增加，本文通过经验公式来确定最佳的 隐含层神经元的个数[12]，即

式中：k为隐含神经层神经元的个数；m为输入层的神经元的个数；n为输出层神经元的个数，a为常数，一般在[1,10]取值.

在建模的过程中若输入原始数据，往往会导致输入层中神经元权重不同对结果产生一定的影响，因此在建模过程中往往对输入层数据进行归一化处理，将原 始数据映射在区间(–1,1)中，即

式中：Xi为归一化处理之后得到的数值；X为归一化处理的对象；Xmax、Xmin分别为原始数据中最大值和最 小值.

1.2 LSTM 数学模型

LSTM 神经网络模型是在递归神经网络(recurr ent neural network，RNN)模型的基础上新增了3 个“门限”结构来替代原有的RNN 神经元，通过输入门限、遗忘门限和输出门限来选择性记忆反馈的误差函数随梯度下降的修正参数，从而实现时间上的记忆功能，并防止梯度消失，假设为输入层数据，为模型的输出结果，则LSTM 记忆单元的状态和输出的计算公式可表示为：

式中：it、Ot和ft分别为t时刻输入门、遗忘门和输出门的输出值；ct、mt分别为神经元和记忆单元在t时刻的激活状态；W为神经网络模型不同层之间的权系数矩阵；b为偏置项；σ为激活函数；tanh为双曲正切激活函数.

2 数据来源和样本训练

2.1 数据来源

本文实验使用的数据包括欧洲定轨中心(Center for Orbit Determination in Europe，CODE)提供的电离层格网GIM 数据，空间分辨率均为2.5°×5°，时间分辨率为1 h；中国科学院空间环境预报中心提供太阳射电通量F10.7数据，时间分辨率为1 d；日本京都地磁数据中心提供赤道地磁活动指数Dst和全球地磁活动指数Kp数据，时间分辨率为3 h. 在实际使用过程中需要将各个数据的线性内插方式得到时间分辨率为1 h 的数据.

2.2 样本训练

本文选择样本数量为2020—2021 年数据，共计731 d，考虑到全球电离层TEC 存在半年/年周期性变化，本文实验数据为抽样选取，以一个月为周期，每个月前20 d 数据作为训练集，中间5 d 为验证集，后5 d 为测试集，若当月天数不足30 d 的，则训练集减少相应的天数，若当月天数超过30 d 的，增训练集增加相应的天数，训练样本结构如图1 所示.

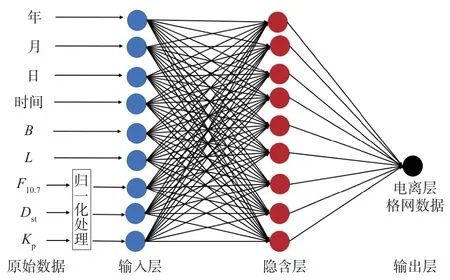
图1 BPNN 模型样本训练结构图

在图1 中，B、L表示格网点经纬度信息，同时将原始GIM 数据进行归一化处理，经过归一化处理的数据能够更好反馈特征项，不会因为某个数量量级过大导致模型精度较差的结果. 通过式(4)确定隐含层的个数为14 个. 样本输入输出数据均为附加时间和空间位置属性的GIM 格网数据.

3 精度评估

将CODE 中心提供的2020—2021 年共计731 d的GIM 数据按照低纬度(22.5°N，65°E)、(22.5°N，125°E)、中纬度(45°N，65°E)、(45°N，125°E)、高纬度(67.5°N，65°E)、(67.5°N，125°E)以月为周期提取各格网点时间序列数据，每个月前20 d 数据作为训练集，中间5 d 数据为验证集来辅助预报模型的构建，后5 d为测试集进行精度评估. 将电离层预报结果与CODE中心的电离层产品数据进行对比，同时以残差的平均值、均方根误差 (root mean square error，RMSE)和平均相对精度作为精度因子进行精度评估. 残差的平均值、RMSE 和平均相对精度分别表示为：

式中：AAVE为残差的平均值；ARMSE为RMSE；ARA为平均相对精度； TECi为第i个历元电离层预报值；TECGIMi为第i个历元的参考值；n为历元长度.

将CODE 中心提供的GIM 产品作为参考值，将低纬度(22.5°N，65°E)、(22.5°N，125°E)、中纬度(45°N，65°E)、(45°N，125°E)和高纬度(67.5°N，65°E)、(67.5°N，125°E)各格网点共计60 d (每月5 d 的预报结果，2 a共计60 d)的预报结果进行对比分析，将最大残差值、最小值、平均值、RMSE、平均相对精度进行统计，结果如表1 所示.

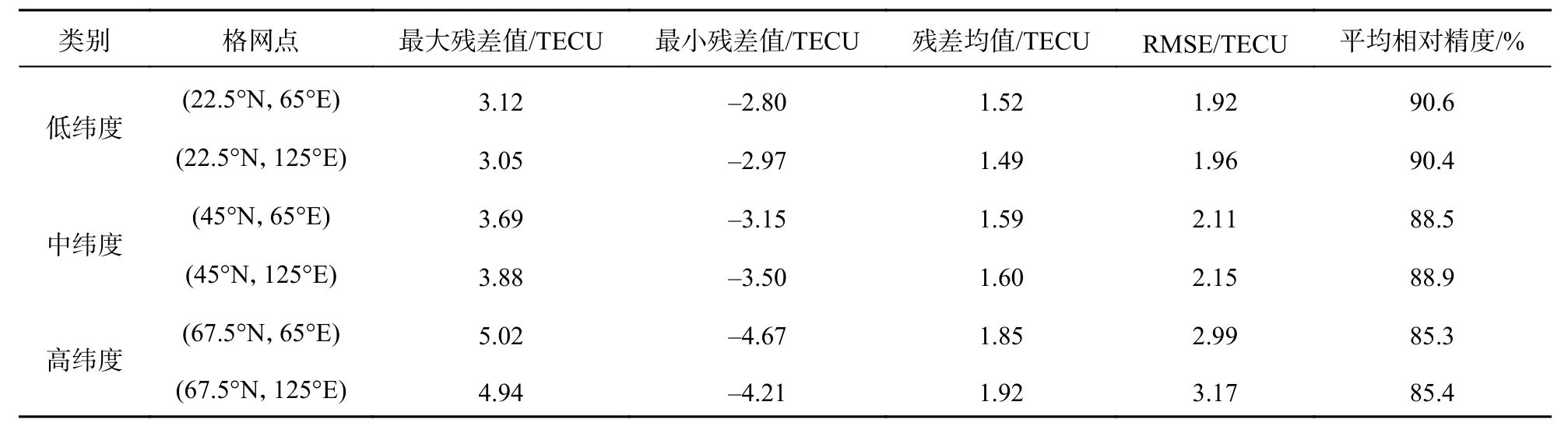
表1 预报电离层各网点残差值统计结果

由表1 可知，基于BPNN 模型预报的电离层TEC 值在低纬度、中纬度、高纬度的预测结果存在差异性，这可能是由于不同纬度地区电离层TEC 值存在较大差异性导致的. 低纬度、中纬度和高纬度电离层格网点TEC 最大残差值分别为3.12 TECU、3.88 TECU、5.02 TECU，低纬度的平均相对精度优于中纬度平均相对精度，中纬度的平均相对精度优于高 纬度平均相对精度，在低纬度地区、中纬度地区、高纬度地区平均RMSE 分别为1.94 TECU、2.13 TECU、3.08 TECU.

为了进一步评估BP 神经网络BPNN 模型在电离层预报中的可靠性和稳定性，将BPNN 神经网络模型电离层预报结果与LSTM 神经网络模型电离层预报结果进行对比分析，结果如图2 所示.

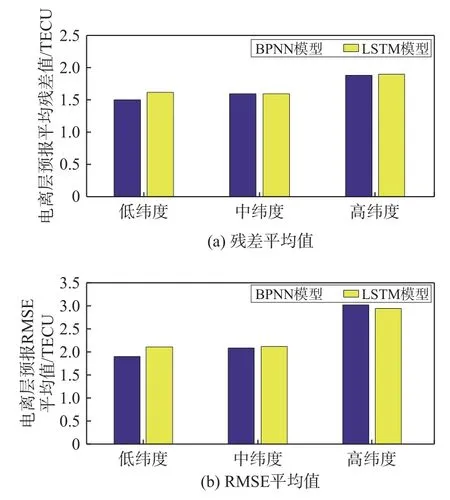
图2 2 种神经网络模型预报精度对比图

由图2 可知，在中纬度、高纬度地区BPNN 和LSTM 神经网络模型对电离层预报均有较好的精度，且2 种神经网络模型对电离层预报精度基本相当.与BPNN 神经网络模型相比，LSTM 神经网络模型在低纬度地区预测的电离层残差值和RMES 值更大，预报精度较低. 因此，在低纬度地区使用BPNN神经网络模型对电离层预报具有更高的精度. 同时，也进一步证实了BPNN 神经网络模型在电离层预报中具有较好的可靠性和稳定性.

4 结束语

针对TEC 时间序列高噪声、非平稳、包含了线性和非线性的动态序列的问题，本文采用非线性预报BPNN 模型将GIM 数据、时间点、经纬度、太阳射电通量F10.7数据、赤道地磁活动指数Dst和全球地磁活动指数Kp数据作为样本训练，同时将预报结果进行精度评估，实验结果表明：

1) 基于BPNN 模型通过样本训练能够较好地预报低纬度、中纬度和高纬度电离层TEC 值；

2) BPNN 模型能够较好地反映出电离层TEC 值的变化特征，在低纬度、中纬度、高纬度的预报残差平均值分别为1.505 TECU、1.595 TECU、1.885 TECU；平均RMSE 分别为1.94 TECU、2.13 TECU、3.08 TECU；平均相对精度分别为90.5%、88.7%、85.35%；

3) 由于电离层时空特性变化机理较为复杂，如何将预报电离层TEC 数据在地震预报、天气预报中取得实际应用可作为下一步重点研究内容之一.