锁相放大器的研究进展*

郭忠凯 李永刚 于博丞 周世超 孟庆宇 陆鑫鑫 黄一帆 刘贵鹏 陆俊†

1) (中国科学院物理研究所,工程师之家,北京 100190)

2) (北京空间机电研究所,北京 100094)

3) (兰州大学物理科学与技术学院,兰州 730000)

4) (大恒新纪元科技股份有限公司,北京 100085)

5) (东南大学电子科学与工程学院,南京 210096)

锁相放大器可同时在时间与幅度两个维度实现高精度信号测量,是精密系统测控的关键部件.本文以锁相放大器的概念、技术与应用的概貌作为导引,先以模拟、数字以及虚拟锁相放大器的主要关系与区分方法说明锁相放大器的发展演变,继而按照锁相环的阶与型从数学角度对锁相放大器进行分类.随后介绍锁相放大器的幅度、频率与相位噪声等主要性能的测试流程与计量标定进展,讨论相位噪声、时域抖动、阿伦方差等关键指标之间的换算关系以及和幅度噪声之间的耦合关联.最后,列举锁相放大器在光谱增强、阻抗分析、磁性测量、显微成像、空间探测领域的应用形式与效果,通过一些新型应用展望它通过智能计算、精准物联等途径从科学仪器走向工业甚至民品的前景.

1 引言

相位反映了信号在时域中的同步程度,也是系统的整体状态演化的重要指示量[1],在电子学中通常由锁相环技术保证对信号相位的精准识别与调控[2—6].锁相放大器是相关检测的一种实现方式,主要利用信号的频率与相位特征从而产生超窄带解调的性能.由于噪声的频率落在通带之内同时相位又一致的概率极小使得噪声被过滤掉,因此锁相放大器能大幅度衰减噪声干扰,实现与设定的频率和相位一致的信号的精准测定[7].典型的锁相放大器架构(图1),主要器件包括内部振荡器、混频器、低通滤波器(LPF),其构造使得输入信号与确定频率的内部振荡信号相乘,相乘后输入信号中与参考信号同频的部分会产生直流分量,输入信号中与参考信号不同频的部分只产生交流分量,经低通滤波将交流分量滤除后则只剩下同频同相位部分产生的直流分量,从而把特定频率的微弱信号从强噪声背景中提取识别出来,有效提高信噪比,甚至可以在噪声幅值超过信号幅值百万倍的情况下实现精准测量.两路来自内部振荡器的一对相互正交信号与被测信号分别相乘并低通滤波后的结果X和Y,经进一步运算后可得输入信号的幅值R和相对内部振荡器的相位差Θ.

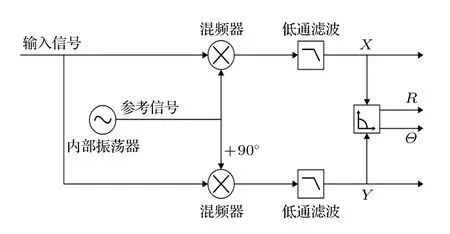
图1 典型锁相放大器原理图Fig.1.Schematic diagram of a typical lock-in amplifier.

锁相放大器主要用于微弱信号检测.微弱信号有两个层面的涵义,一方面是指被检测的信号幅度本身很微弱,另一方面是指被检测的信号相对于噪声幅度非常微小,即所要检测的信号淹没在噪声中.为了检测被噪声淹没的微弱信号,人们进行了长期的研究工作,分析噪声产生的原因与规律,研究被测信号的特点、相关性及噪声的特性,以寻找从噪声中检测出有用信号的方法.锁相放大器是诸多微弱信号检测方法中检测能力强、可靠性高的一种成熟的方案,因而在检测微弱信号(如弱光、弱电流和小电容等)中有着广泛的应用,使微弱信号测量精度得到了很大提高.对于幅度较小的直流信号或慢变信号,为了防止低频噪声和直流放大的直流漂移(例如运算放大器输入失调电压的温度漂移)的不利影响,一般都使用调制器或斩波器将其变换成交流信号后,再进行放大和处理,用带通滤波器抑制宽带噪声,提高信噪比,之后再进行锁相解调,以得到高信噪比测量[8].锁相放大器充分运用了以锁相环为典型技术的相位调控技术来保证时间同步,并且针对微弱信号进行幅度放大与精密测定,故而在约80 种重要科学仪器中被当作核心部件发挥重要作用[9].

锁相放大器中核心部件的最初雏形在1931 年由一份英国专利公开[10];1947 年,锁相环第一次应用于电视接收机水平和垂直扫描的同步系统[11];第一台锁相放大器1962 年在美国EG&G princeton applied research corporation (PARC)公司问世(现属 SIGNAL RECOVERY 公司);大约在1965 年,锁相环集成电路诞生,尽管一开始的集成锁相环是类似于运算放大器的半导体器件.1970 年数字锁相环(DPLL)随之问世[2];近些年,在成熟的锁相环集成电路技术推动下,能够实时跟踪外部参考信号进行微弱信号测量的集成锁相放大器微系统[12].通过对2023 年市面上典型的锁相放大器产品性能指标等信息进行汇总[13—21](列表对照如表1 所列),不难看出近几年各品牌都在陆续推出高性能的锁相放大器,比如中山大学及其孵化企业赛恩科学仪器公司在2020 年推出60 MHz 带宽的产品,同时也在积极进行最高600 MHz 带宽与140 dB 大动态范围的高频锁相放大器的商业化;澳大利亚Liquid Instrument 公司于2021 年推出相位噪声指标宣称达1 nrad·Hz1/2的锁相放大器;瑞士苏黎世仪器公司于2022 年推出最高8.5 GHz带宽的超高频锁相放大器.表1 中列的指标是2023 年初获取的厂家标称数据,部分数据随着时间推移会有出入,如有差异,请读者以当时从厂家获得的更新数据为准.通常,厂家标称值与用户体验值之间的差异,不同型号产品之间波动会较大,要综合看厂家风格趋于保守务实还是冒进,还受仪器状态、用户环境等因素影响.

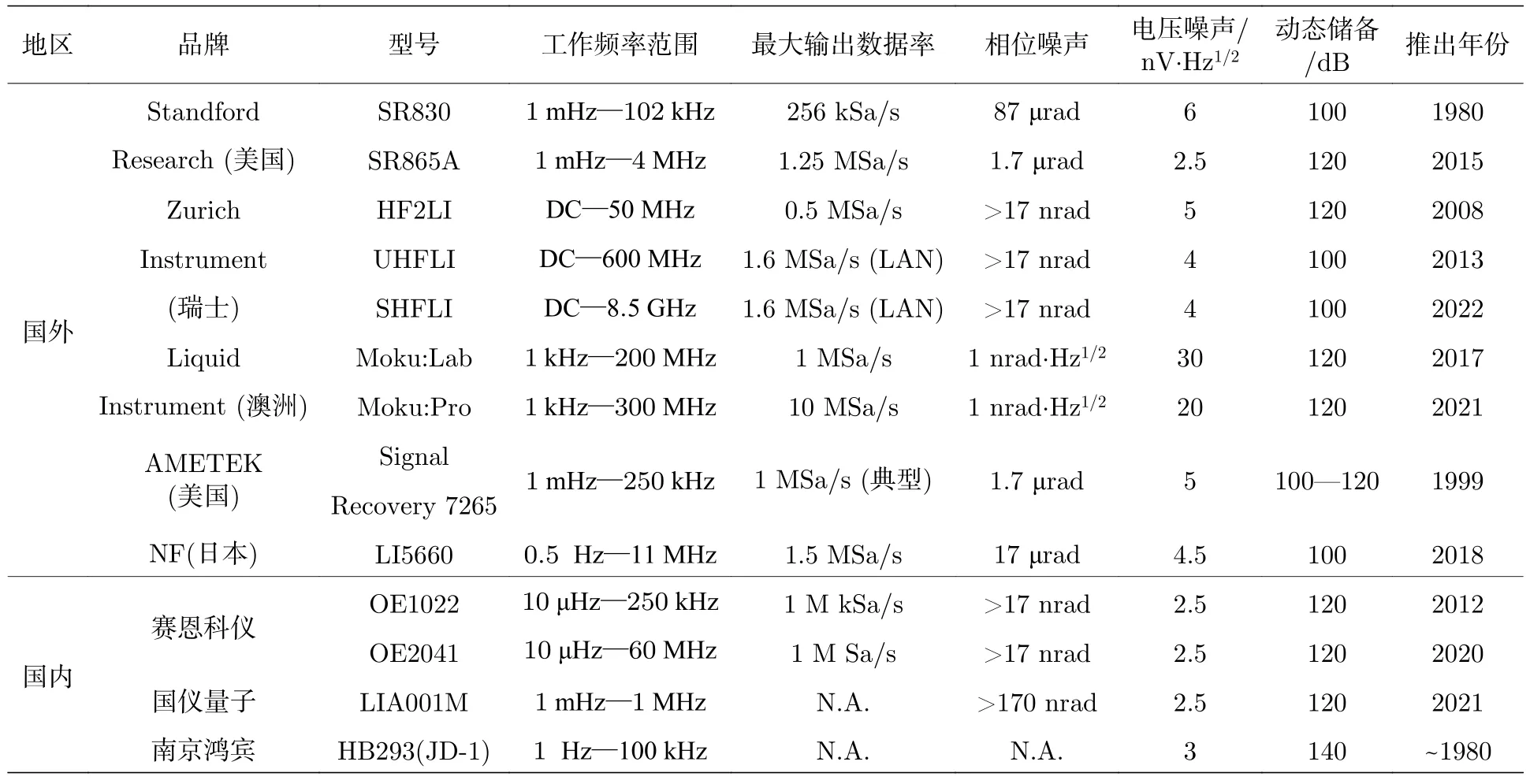
表1 国内外目前锁相放大器产品性能指标的对比Table 1.Comparison of performance for current available lock-in amplifier products around the world.

为了给出近些年锁相放大器的研究与应用概貌,本文借助CiteSpace 聚类分析技术[22],以锁相放大器及其直接关联的两大关键词(“锁相环”与“信号幅度”)进行知网中近40 年已发表文献的关键词聚类,结果如图2 所示.锁相环作为精密的时间管理部件,更加关心信号的同步性能,比如抖动、相位噪声与谐波干扰等底层时频特征;兼顾锁相环性能与信号幅度测量的锁相放大器,更多的研究关注其场景性能,比如热导、交流损耗、太赫兹光谱、光声光谱等具体的应用系统;尽管3 个关键词聚类拓扑网络结构相差较大,锁相放大器跟锁相环与信号幅度分别在“谐波检测”与“信噪比”两个从属关键词上,具有一致的研究热度,反映出锁相放大器与锁相环及信号幅度之间的内在关系.

需要指出的是,并非所有的锁相放大器中都具备锁相环,二者的内在结构相异,但也有交叉.如图3 所示,锁相环的主要特征除了相位同步之外就是控制成环,即结构图中存在反馈路径,从而实现精密滤波的功能;锁相放大器除了时间同步之外还关注信号幅度的精密测量,从而实现精密解调功能,并没有指明是否有反馈环路,故而与锁相环之间有交集、但不重合;兼具锁相环与锁相放大器二者的仪器中,既有以锁相环为主、辅助传感器和控制器对物理系统进行闭环精密测控的仪器(其中相位检测使用锁相放大器部件),也包括锁相环内核式的锁相放大器(参考信号通过内部锁相环后能大幅度提高测量精度,但主体框架以信号测量路径为主).经过对锁相放大器的概念、功能和结构的概括介绍,接下来对其分类、检测方法以及典型应用方向在近些年的进展相继进行介绍.

图3 锁相环与锁相放大器结构关联与差异示意图Fig.3.Schematic diagram of structural correlation and difference between phase-locked loop and lock-in amplifier.

2 发展及分类

2.1 模拟锁相放大器

最初的锁相技术用于通信,其中的编码解码过程一般只关心信号有无,而信号的绝对强弱程度相比较而言并未引起关注,但锁相技术给微弱信号测量带来了全新的思路,即将模拟信号中最难解决的信号同步交给锁相环,而信号强弱通过相敏检波的手段测量并获取.

在这样的思路指引下,1962 年问世的第一台锁相放大器属于全模拟锁相放大器(analog lockin amplifier,ALIA),其核心部分由信号放大调理、相敏检测器(PSD)与低通滤波器(LPF)三部分构成.信号通道的主要作用是对输入信号进行交流放大,将输入的微弱信号放大到可以适合PSD工作的电平,并对输入的微弱信号进行滤波,除去不相关的噪声和干扰,提高系统的动态储备.输入到参考通道的参考信号可能是正弦信号或者方波信号,参考通道的主要作用是将输入的参考信号转换成系统可以识别的方波信号,参考信号通道输出后系统将此方波信号转换成用于PSD 的正弦信号,同时,参考信号通道可以对输入的参考信号移相,使输出信号达到所需的相位要求.PSD 是锁相放大器的核心模块,它的主要作用是将输入信号与参考信号相乘,实现对输入信号和参考信号的和频和差频运算.LPF 的作用是对PSD 输出信号进行低通滤波,去除PSD 结果中频率较高的和频项和噪声,输出直流结果,即差频结果[9].

随着数字技术的发展,ALIA 中逐渐也出现了模数转换器、数模转换器和微控制单元用于锁相放大器的控制、接口和数字显示,但是这个阶段的锁相放大器仍然是属于ALIA,因为其核心部件PSD和LPF 仍然是采用模拟电路实现的.基于相关处理的ALIA,当积分时间无限长时,噪声可以完全抑制,从而利用ALIA 可以准确测得微弱正弦信号(或周期信号)的参数.但实际上由于受到电容漏电的影响,积分时间不能很长,检测缓变周期信号的效果变差.同时在测量纳伏级电压时,乘法器输出电压小,后接的直流放大器零漂严重,妨碍了对极弱信号的准确测量.此外,模拟乘法器或开关门是模拟器件,其线性决定了相关运算的精度,但其线性很难保证,容易饱和,线性范围小,温漂大,使得系统受到很大限制.还有,模拟系统里面有很多滤波器,其性能都受到模拟器件性能的影响,进而影响整个系统的性能,这些问题都是模拟系统很难克服的.

总的来说,ALIA 除了系统性的漂移缺陷之外,模拟器件引入的直流分量限制了系统对信号的放大,让动态储备很难提高;另外,模拟器件本身的噪声较大,一定程度上限制了最低可检测信号的信噪比.不过,由于模拟器件的极限响应速度能达到纳秒以下,故而在对锁相带宽或响应速度要求特别高的场景中,至今仍然在使用.

2.2 数字式锁相放大器

为了解决ALIA 的前述不足,数字锁相放大器(digital lock-in amplifier,DLIA)应运而生.DLIA的基本原理同ALIA 相似,但相关的主要器件如振荡器、乘法器、LPF 包括信号大小表示均用数字逻辑电路实现,如图4 所示.具体结构常包括测频模块、鉴频鉴相器、数字滤波器、正弦振荡器、模数控制器、数字LPF 和正弦波整形电路模块.目前国外苏黎世仪器、Liquid Instrument 与国内的赛恩科学仪器推出的先进DLIA 都运用直接数字合成器(direct digital synthesizer,DDS)与FPGA (field programmable gate array)组合技术.用DDS 的优点是需要较短的计算时间,同时产生的激励正弦信号在幅度和频率上有极好的稳定性和准确性;FPGA 内部主要包括逻辑阵列块(logic array block,LAB)、内部连线(interconnect)、输出输入模块(input output block,IOB)三个部分.乘法器主要是针对数字信号处理方面的运算需要,乘除运算在底层的硬件上实现并不是那么容易,一次乘法运算依次执行各步运算需要消耗几个小时,不过经过流水线优化处理后1 h 也可以完成任务,很多内嵌的乘法器模块也给运算处理带来方便.

DLIA 的工作过程为参考信号经过整形输入到FPGA 后,测频模块首先对其进行频率测量,并把频率值输入到正弦振荡器,正弦振荡器输出两路相位相差90°的正弦信号,其中一路正弦信号通过模数控制器输出后,由LPF 和正弦波整形电路将其整形为方波后反馈回FPGA,在FPGA内部通过鉴频鉴相器比较参考信号输入和反馈信号,并将经过滤波后的比较结果输入到正弦振荡器,正弦振荡器再根据这个比较值调整频率和相位,最终使输出的正弦信号与输入的参考信号锁定,进而实现微弱输入信号的精密测定.

然而DLIA 系统性能也因其自身原理会受到4 个因素的影响.

1) 积分时间常数,DLIA 的时间常数是一个相应于ALIARC 值的数字积分时间常数值.由随机信号的统计特性可知,当锁相放大器时间常数变长时,输出端将变得更加稳定,而且所测值更接近于实际信号.DLIA 克服了模拟器件的一些固有缺陷,但其自身的积分时间并不严格被界定,而是一个可以编程的量值.且理论上,DLIA 积分时间常数可以为任意值.由ALIA 理论可知,DLIA 的系统锁相精度正比于N,其中N是数字系统的累加次数,相应于模拟系统的积分时间常数.在信噪比SNR 较低的情况下,该值对系统的锁相结果误差影响很大: 积分时间常数越长,则系统的输出信噪比SNR 和系统锁相精度将更高.但是在达到一定的检测精度条件时,延长系统的积分时间对于系统锁相结果的改善却并不明显,而与此同时,系统的开销(包括存储、运算等)将成倍增加.故积分时间常数选择是否适当是影响锁相放大器系统的一个重要因素.

2) 频率偏移.我们知道用普通模拟电子器件生成的周期信号,其频率可能受时间、温度、电压稳定度等因素影响,产生较大偏移.而数字的周期频率信号,由于数字元件的有限字长和DAC 参考电压的稳定性,其频率偏移将会变得较小,但仍不可避免.故对于数字锁相系统,必须清楚地知道同步参考与被测信号频率不是完全一致时对系统锁相结果的影响.

3) 采样频率,对于一个确定的系统,系统的采样频率必然为有限值,由奈圭斯特定律可知,系统可恢复的最大信号频率为采样率的一半,而信号被有限采样的结果是导致失真.

4) 数字锁相运算的数据类型.由于数字系统存在有限字长误差,系统数据类型的选择也是必须考虑的因素.一般地,对数据类型的选择一方面由ADC 和DAC 的位数决定,位数增加必然延长响应时间、牺牲锁相效率;另一方面,通常乘法的数值运算中,单精度浮点类型是比较合理的选择: 既可以满足不产生积分溢出,又可以在不导入后期数据运算误差的基础上减少系统运算量,而如果采用定点数据类型则会产生积分溢出,采用双精度数据类型则要消耗大量的运算开支,影响系统实时性,而且随着积分时间的增加,这种误差会积累变大.故而数字锁相中,合理选择ADC,DAC 和所匹配的数据类型是必要的.

在设计具体的应用系统时,考虑以上因素是获得高性能DLIA 的重要步骤.

2.3 虚拟锁相放大器

虚拟锁相放大器是全部用CPU 等计算处理器运行软件来实现相敏检波等核心功能的一种仪器.如图5 所示,在虚拟锁相放大器中,其组成部件振荡器、乘法器、LPF 主要由处理器的指令代码和数据流来实现,从而成为一种特殊的算法,数据处理上具备极大柔性.虚拟仪器的核心竞争力在于自由、灵活且方便地联系真实世界与仪器用户,也被称作软件锁相放大器,实质上是用软件直接实现解调算法的锁相放大器.

图5 虚拟锁相放大器中由CPU 等指令工作流完成所有运算Fig.5.In the virtual lock-in amplifier,all computations are accomplished by the CPU instruction workflow.

据查,1998 年开始有虚拟锁相放大器的报道[23],它让微弱信号测量的门槛明显下降,由于软件的载体多种多样,即便使用成本非常低的单片机,加上模数与数模控制器,即可通过虚拟线路与软件实现锁相功能,并能为PLL 提供对—40 dBp 的高噪声的抗扰性同时确保其高动态性能[24].虚拟锁相放大器还可以由用户自行定制多通道并组合用于复杂的应用测量系统,精度与效率相比传统ALIA 均呈现出优越性[25].虚拟锁相放大器及基于它的应用系统,通过Labview 与FPGA 等源代码开放来加强研发和应用的联系,对锁相放大器的发展有明显的推动[26-28].

虚拟仪器的另一个突出优势,是算法更新升级周期可被大幅度缩短,容易探索新型锁相,比如新型测频式锁相放大器[29],一定的时间长度与采样率条件下频率测量不确定性存在统计学上的下限,即Cramer-Rao 下限,在不同信噪比条件下的测频精度接近理论下限;更进一步,经过理论推导出单周期信号的锁相频谱在估计频点附近的局部函数形式,证明正确的余弦峰函数形式优于经验的抛物线,并基于此使用较少的计算量就能实现精确测频,当数字处理信号长度为N时,相比FFT 的复杂度O(N·logN),新算法的复杂度减为O(N).

为了方便对上述3 类锁相放大器的主要特征进行鉴别,图6 给出从模拟信号经过锁相放大器变成软件数据的过程,不难看出ALIA 的硬件与软件界限在锁相处理后端;DLIA 的硬件与软件界限前移到解调器,甚至更前;而虚拟锁相放大器的核心解调功能则完全用软件实现.狭义的DLIA 和虚拟锁相放大器的区别是有无数字逻辑硬件,不过随着数字信号处理(DSP)与FPGA 等可编程数字处理芯片技术的发展和应用,二者的界限变得模糊.此外,鉴于模拟、数字、虚拟锁相放大器各有优缺点,为了实现性能最好的锁相放大与微弱信号提取性能,将三者充分结合是必然趋势,即充分利用模拟前端进行被测信号的调理,运用虚拟锁相迭代并测试出原理最优的算法,最终用高速数字电路实现大动态范围、极低零漂与噪音隔离.

图6 模拟、数字与虚拟锁相放大器的分类标准图示及说明Fig.6.Schematic description of classification criteria for analog,digital and virtual lock-in amplifiers.

2.4 数学角度的分类

任何仪器无论实现形式是机械、电子还是软件,其工作状态都可用数学模型近似描述,锁相放大器也不例外[4].从数学角度,锁相放大器尤其是高精度锁相放大器的核心锁相环的设计与实现在可线性化处理时主要使用传递函数分析[2,3].通过传递函数可以定义良好描述锁相环工作状况的重要概念型(type)与阶(order),他们分别按照积分器个数与闭环传递函数分母多项式最高次数(极点个数)来定义[3,5].阶数比较容易理解,其物理含义是锁相环时域动态微分方程中对输出信号的最高微分次数,而积分器并非物理器件(比如电容等器件),是数学意义上输出相位的开环总响应信号随时间积分的重数,对应拉普拉斯变换到s域后的开环传递函数中1/s项的总次数(位于原点的极点个数)[30,31].关于锁相环的型与阶的传递函数与结构性能关系,本文稍作展开讨论.

锁相环一般由相位检测器、环路控制器以及受控振荡器三个部件组成,其中相位检测器与受控振荡器在线性近似下具备统一不变的结构,因此影响环路传输主要性能的部件只有环路控制器.模拟环路控制器根据是否需要电源工作的元件分为有源与无源两类,而控制器电路的无源元件通常都由电阻R 与电容C 组成的网络实现,其中RC 组合用于调节比例积分以及更为复杂的功能.

为了让型与阶的关系理解起来更加具体,本文对3 阶III 型及其以下的各种组合的几种典型的锁相环进行了综合图示和对比,如图7 所示,每种阶与型组合在这里只选取一套电路与传输函数,并不排除还有其他形式的具备相同阶数与型数的实现结构.相关型与阶的举例结构、数学式以及功能的对应关系要点如下.根据阶与型的定义,由于开环零极点个数不大于闭环极点的个数,锁相环的型数也不大于阶数,故而图7 的组合矩阵中只在上三角有实际意义,而下三角没有存在的可能性.

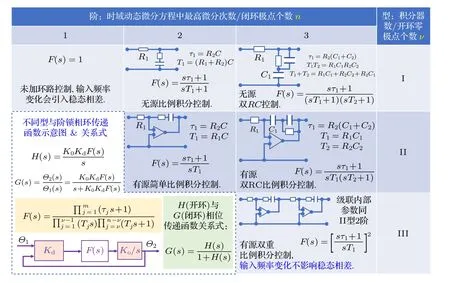
图7 锁相环的型与阶分类以及典型结构功能与表达式列举示意图Fig.7.Schematic diagram of the type and order classification of phase-locked loops and the enumeration of typical structural functions and expressions.

最简单的相位检测器与受控振荡器之间直通的结构为1 阶I 型锁相环,输入信号频率稍有变化就会带来相位误差的不断累积,故而不在实际仪器中被采用.一般而言,阶数越大型数越大的锁相环对输入信号的跟随能力越强,但稳定性更不易维持.

I 型锁相环只能跟踪相位变化而不能稳定准确地跟踪频率阶跃信号以及更快速变化的频率斜升信号.当阶数增加到2 或3 时,能够更快地锁定并跟踪输入信号,增加了捕获带宽.图7 中举例的无源RC 结构是一种常见的2 阶I 型环、3 阶I 型环.

对于II 型锁相环,阶数至少为2,能够准确跟踪相位阶跃和频率阶跃信号,不能准确跟踪频率斜升信号,跟前述2 阶I 型锁相环举例电路相比,因为有源反馈将积分RC 的零电位固定,相对应的极点从非零移动到零,尽管阶数维持不变(捕获时间保持不变),但型数增加到2,且引入了有源增益,改进了稳态相差.

当型数增加到III,阶数也必然大于或等于3,即不仅能够跟踪相位阶跃与频率阶跃信号,还能够对频率斜升信号进行稳定准确跟踪,比如图7 中用双重有源比例积分电路实现的例子.3 阶III 型以上的锁相环,由于其复杂性会带来对干扰信号抑制能力的下降,稳定性难以保持,良好的参数集不易获得.

以上只对锁相环的典型类型的结构与性能做了定性比较,实际上具体的锁相环中因为结构参数的变化,简单的理论分析和理解是不够的,而是需要借助数值仿真工具进行系统分析,比如以色列本古里安大学的Wulich 和Bar 教授[32]提出参数可自适应型锁相环,并以比例积分型锁相环为例,使用积分与比例控制参数可变的策略,设计可重构柔性参数锁相环,让收敛锁定时间缩短30 倍;又如西班牙纳瓦尔公立大学的Ugarte 与Carlosena[33]讨论分析了具体的锁相环的类型差异,证明了II型和III 型都能够跟踪变频率,二者性能的主要差异有两个: 一是II 型锁相环存在非零相位误差信号,而III 型锁相环中的相位误差信号保持为零;第二个更重要的区别是一旦频率变化率越过极限,II 型锁相环将容易失锁,而III 型锁相环在经历一段时间后可以重新锁定.除此以外,II 型与III 型锁相环的零点频率与能承受的最大频率变化率之间存在准线性关系,而极点的数量和位置不影响锁相环对啁啾变频信号的跟踪能力.

当然,除型与阶之外,从数学的角度分类,还可以从动力学稳定性以及拓扑结构进行分析,由于其重要性与广泛性比不上型与阶,而且已有专著进行总结[34],故本文不展开讨论.

另外,在高性能锁相放大器中为了实现对特定外部参考信号的精密测定和跟踪,通常要考察数字检相器、数控振荡器和量化噪声等因素的非线性影响,因此线性化传递函数可能不足以充分描述全数字锁相环[17],需要根据其实测的动态性能来进行分析、调整和优化.

3 测试方法

3.1 测试流程

锁相放大器的核心功能是从噪声中提取单频信号的幅值和相位,对应的测试方法也是对其测试结果的精准度进行判定.评价锁相放大器的幅度、相位与噪声的提取能力的测试系统如图8 所示,通过任意波形发生器生成设定频率、相位、幅度的测试信号(根据需要,还可以进一步复合噪声),继而让被测试的锁相设备对该信号进行测量与处理,并对其输出进行采集分析,综合设定信号与测量分析信号的偏差以及不确定度,从而评定被测锁相设备的幅度与相位的测控性能.

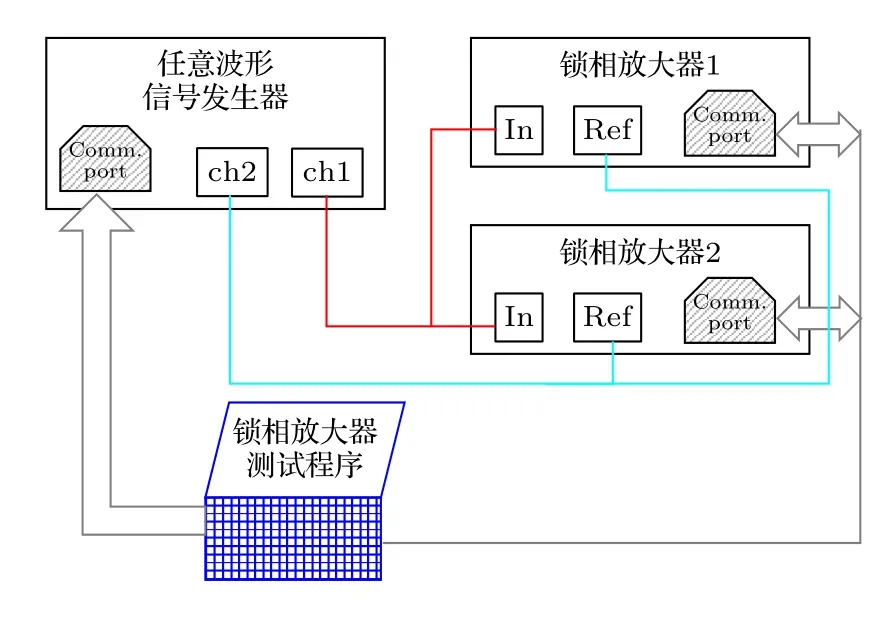
图8 锁相放大器的典型测试系统各部分连接关系图Fig.8.Illustration of a typical test system for lock-in amplifiers.

具体的测量流程如图9 所示,首先让设备开机预热半小时以上、准备好测试屏蔽线缆与50 Ω 负载端子,并启动测试软件.如果要运行电压底噪测试,应将输入端用50 Ω 负载短接,设定内部参考模式,将锁相解调频率和时间常数设置成被考察值,比如997 Hz 和1 s,然后连续多次记录,为了确保多次记录值之间相互独立无关,相邻次的记录间隔不少于3 倍时间常数.记录完不少于10 次测量结果后(实部虚部或幅度相位差),如果预先知道测量时锁相设置对应的等效噪声带宽(ENBW),直接对每次测量结果的幅度均方值进行平均,并除以ENBW 的平方根,即得到噪声谱密度(单位:V/Hz1/2).

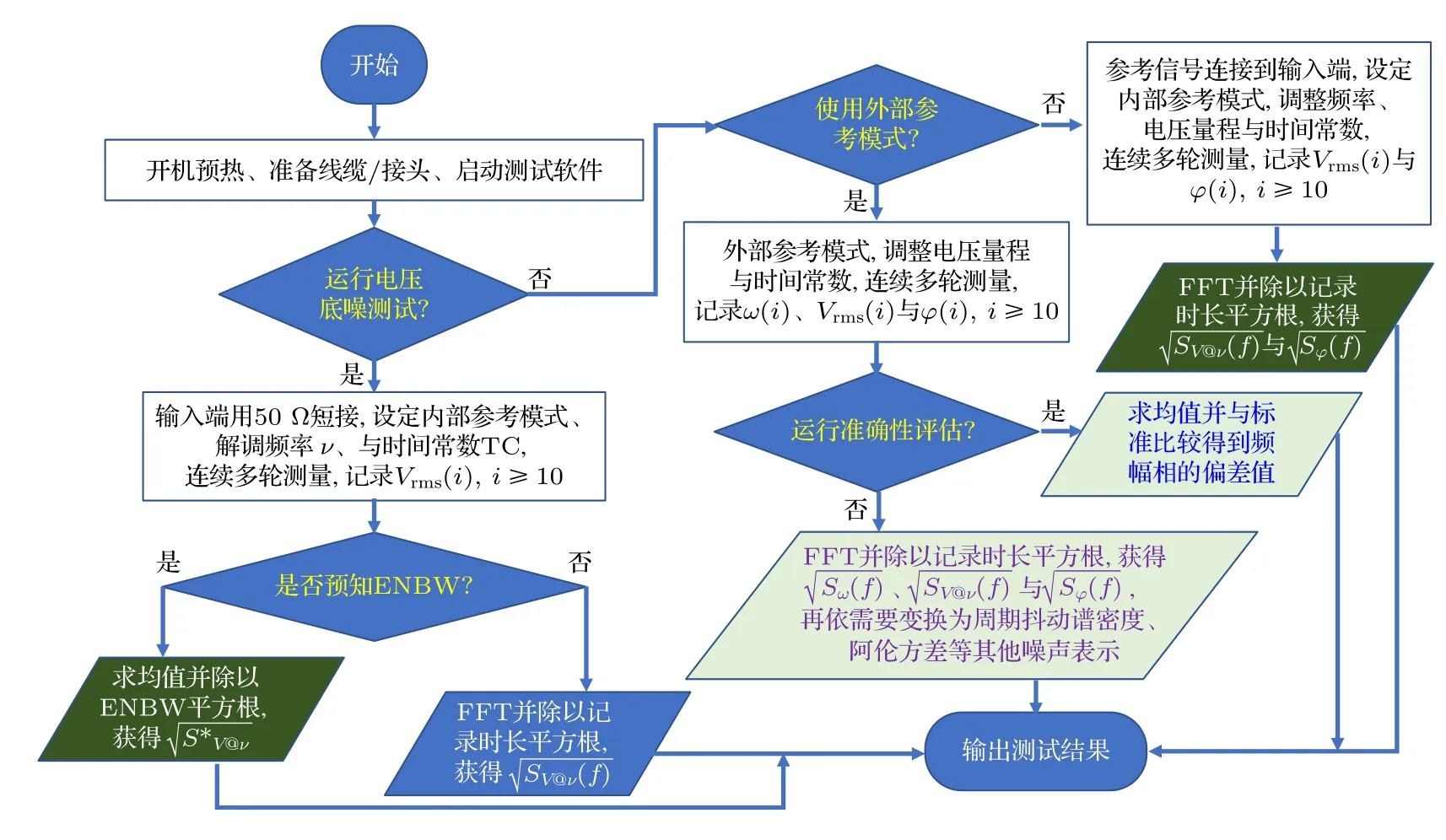
图9 锁相放大器的幅度、频率与相位测量不确定度性能测试流程图Fig.9.Flow chart of evaluation process for lock-in amplifiers,to obtain performance on measuring amplitude,frequency and phase.

当被测锁相放大器的ENBW 不能预知时,在经典的SR830 与SR865 锁相放大器中,依照高斯噪声分布规律,在RC 滤波滚降在6 dB/Oct 条件下,按时间常数的倒数乘以系数0.25 来计算(滚降为12 dB/Oct 时,系数为0.125),即此时1 s 时间常数的ENBW 为0.25 Hz,如997 Hz 下1 s 时间常数多次RMS 测量电压结果的平均值是1 nV,此时测得该锁相测量条件下的电压噪声谱密度为1 nV/√0.25 Hz=2 nV·Hz1/2.当用户对锁相的滤波参数不清楚,或滤波器类型并非经典的RC 滤波器时,通常情况下锁相频谱是单峰,ENBW 估计可从频谱峰值着手,即锁相在被测频率附近扫描标准单频信号得到频谱的功率频谱面积除以功率峰值来估计,按简单正弦波的扫频锁相均方幅值频谱的经验估计,ENBW 近似等于最大值往高频或低频到第一个最小值之间的频差;当频谱比较复杂而不能简单看作单峰的时候,功率峰值以功率平方谱的面积除以功率谱的面积来计算[35].

从ENBW 的估计过程可以看出,它对锁相频谱的形状比较敏感,因而具有一定的局限性,如果不管ENBW 参数,也可通过快速傅里叶变换(FFT)将电压底噪的RMS 幅值锁相测量变换成模值频谱,并除以观测总时间长度的平方根,进而得到电压噪声谱密度.电压噪声谱密度,其平方之后的物理意义即对应功率谱密度,除非特别说明,此时假设电压作用在1 Ω 的电阻上,从而保证二者的等效性.功率谱密度的处理过程在被测信号并非电压信号(比如相位差和频率)时,结果的物理意义明显偏离功率的含义,不过在确保时域和频域之间变换的等价性方面,频谱密度仍然被作为重要物理量而经常在锁相放大器相关的研究中被应用.通过FFT从时域信号到谱密度的变换过程中,需要注意: 如果是模值频谱(magnitude spectrum),即从原始FFT 定义在时域积分的结果(单位: V·s),除以观测电压序列数据的总时间长度的平方根或乘以FFT 频谱分辨率,得到电压噪声谱密度;如果是幅度频谱(amplitude spectrum),即模值除以时间长度(单位: V),乘以观测电压序列数据的总时间长度的平方根或除以FFT 频谱分辨率,得到电压噪声谱密度.二者混淆容易导致错误变换,比如用幅度频谱除以FFT 频谱分辨率的平方根、或用幅度频谱乘以时间长度平方根,得到的结果跟噪声谱密度不符.此外,经过FFT 到谱密度的换算工具中,不同的软件平台稍有不同,如窗函数选取、变换步骤、参数名称等,但只要对处理过程清晰了解,并不难获得准确一致的结果[36].

除了电压底噪,锁相放大器的评价还要看它对确定频率和幅值信号测量的准确性和不确定度.如图9 所示流程图的右半部分所示,总的来说有外部参考和内部参考两种,虽然内部参考能够获得幅度与相位噪声信息,而且操作相对简单,但是外部参考模式下能够更加全面地对锁相放大器解调性能的精准程度,而且其噪声分析过程也能够覆盖内部参考模式,故而这里侧重介绍外部参考模式测试.参照图8 中的接线与控制,给锁相放大器输入设定频率和幅值的信号,调整锁相解调频率和时间常数并启动测试,然后连续多次记录,为了确保多次记录值之间相互独立无关,相邻次的记录间隔不少于3 倍时间常数,然后记录并获得不少于10 次频率及对应的复数测量结果,如果是实部虚部,则换算成均方幅度与相位差.对锁相测量结果的准确性测量和标定,需要将测量结果跟设定频率与电压幅度进行比较,获得系统偏差值;而对精确性进行评估,则将测量的频率、幅度和相位差的多次测量结果,通过转换到频率谱密度、电压谱密度和相位差谱密度,获得综合噪声性能,其转换方式与前述电压噪声谱密度一致.对于锁相放大器的相位噪声性能,除相位差、频率之外,还有时域周期抖动(jitter)与阿伦方差(Allan variance)等表示方法,给锁相应用中信号的同步程度要求提供更加丰富的选择[37].多种相位噪声表示之间具有非常强的内在联系,具体的相互换算关系,将在3.3 节展开综合分析.

在噪声中提取信号是锁相放大器的重要功能,那么信噪比的提升水平的定量评价就非常重要,相同条件下,对信噪比增减进行相对比较,进而获得器件或系统的噪声系数或噪声温度,该方法已经很常用[38].不过,因为非陷波的白噪声中特定频点分量不固定,尽管有一些锁相陷波与信号合成的方案,比如闭环前馈与反馈陷波[39]、与数字锁相陷波与信号合成方案[40],目前还没有统一的方法进行标定测试,本文不予展开.

3.2 计量与标定

随着锁相放大器应用的推广,电子测量与仪器行业逐渐开展锁相放大器的计量规范与标准制定工作,2020 年中国电子科技集团公司第十研究所等单位通过全国无线电计量技术委员会起草了一项《锁相放大器校准规范》,不仅包括频率、幅度和相位差三项主要功能,还对共模抑制比、直流输出电压、内部参考输出幅度、校准不确定度评定等测试过程制定了规范[41];大恒光电于2022 年制定了《OE2042 精密大带宽锁相放大器》企业标准,除前述核心功能之外,还对频率范围与分辨率、动态储备、电气适应性、上位机功能以及定性检验都进行了规定[42].

在锁相放大器的计量过程中,幅度、相位、带宽与信噪比的标定,通常离不开经过计量校准的信号源,在前述校准规范中,也都是采用从电压基准间接传递过来的信号源,为了进一步提高测试信号的准确性,近些年在交流信号基准方面也有一些进展.河北大学王彪与中国计量院张江涛等[43]利用四端互感将锁相放大器溯源到交流电压标准和交流电阻标准上,进行锁相放大器正交分量的溯源,以四端互感和三支路电抗分流器为基础,在量程5 mV,20—200 kHz 频率之间对锁相放大器进行校准,不确定度评定结果在4/1000 以内.意大利国家计量研究所Cultrera 研究组[44]开展了锁相放大器在低频范围内的校准,通过欧洲跨实验室锁相标定比对,显示亚千赫兹频率与微伏幅度下,锁相放大器的相对不确定度在1/10000 量级.中国计量院贺青团队[45]组合NIST 的电阻量子基准和原子钟频率标准,完成锁相电压的交流量子基准测试,在60 Hz 频率下1 V·rms 的不确定度达到亿分之五.中国计量院的陆祖良团队[46]经过演示性实验表明,交流电压基准的相对误差在技术上可以实现1/105.从信号分析角度,由模数控制器产生的模拟正弦信号,实质上是阶梯波的基波,而量化过程将使此基波相角与其设置值产生偏差,即相位的量化误差.当设置相角在 0—360°之间变化时,相位的量化误差呈现周期性重复现象,而且在固定相位处的量化误差为零,因而可通过调节相位值与数模转换器的分辨率消除相位的量化误差[47].

3.3 综合噪声分析

噪声大致分为相位噪声与幅度噪声两类,其中相位噪声具体包括时域周期抖动与频率波动,不过二者通常被统称为相位噪声[48].相位噪声相关的物理量相对复杂,而且容易混淆,为了清晰揭示多种相位噪声表示之间的内在关联,本文将各个量与单位及其相互变换关系式统一进行介绍.总的来看,诸多噪声物理量分成时域和频域两种,如图10所示,时域噪声量通过FFT 变换后平方除以总时间长度,得到对应的频域噪声谱密度.对应地,时域角频率与相位差之间的微分关系变成谱密度中的变频率参数,而相位差与时域周期抖动之间只是相差固定频率系数.角频率的时域变化信号,通过将一定的时间间隔进行分块,对每块求平均值并对相邻块的平均值的差值求相对方差,得到阿伦方差,由于使用设定时间长度分段时域差分的方式,相比频率与相位差谱密度,不仅能更直接地在时域上看出噪声来源属性,而且将相位噪声的随机行走与白噪声来源分别以正斜率与负斜率进行明确区分,从而有助于分析其特征细节[37].

图10 锁相放大器的诸多噪声抑制性能及其相互转换关系示意图Fig.10.Various indicators of noise suppression properties and their relationship for evaluating lock-in amplifiers.

关于相位噪声模型中5 项关键模块的分项贡献,杜克大学的Morizio 研究组[49]以锁相环作为载体做了分析,即过采样模数转换器、相位频率检测器、电荷泵、LPF 和压控振荡器,提出了简单易用的公式来预测总相位噪声.相位噪声的重要体现形式在时域抖动,经过相位噪声起源的研究,Demir 教授[50]找到一种时域抖动与相位噪声之间的简易跨域换算关系,并运用系统的仿真模拟进行了有效性检验.从时间序列数据到功率谱密度的具体计算过程,在网络上已有文档予以总结并公开(通过Matlab,Labview 以及Origin 等工具举例)[36].

为了量化评估锁相放大器的噪声以及传递函数性质,通常采取信号通道上多节点同步矢量宽频监测,通过跨时频分析获取锁相环或锁相放大器噪声性能的评测[51],并根据需要与模拟仿真结果进行比较,从而辅助优化与改进设计[52].根据多种方法的测试效果对比,意大利Sannio 大学Eulalia 等[53]指出相位测量不确定度最低的锁相方法来自于正弦拟合方法.相比之下,频域局部拟合的锁相测试方法是目前最有竞争力的精准测频锁相方法之一[29].

虽然简单正弦模式产生和叠加成测试信号过程中,幅度噪声与相位噪声之间独立不相关,但运用锁相放大器对信号的幅度噪声与相位噪声进行解调反演过程中,不可避免出现相位噪声影响幅度噪声测量结果,或幅度噪声影响相位噪声测量结果,所以对被测部件或仪器内部结构不清楚的情况下,对二者的准确解耦和分离尽管意义重大,却存在很大的挑战性[37,54].

为了直观地认识噪声指标,这里以表1 中列举的相位噪声指标最高的Moku:Pro 产品为例(1 nrad/·Hz1/2),讨论综合分析的过程.在不知道Moku:Pro 的内部结构和软硬件实现细节的情况下,从可查到的多项性能指标估计出获得最佳相位噪声指标应采用的前提条件: 相位噪声的测量结果在锁相放大器同时受时钟噪声、电压噪声与模数转换器量化噪声影响,那么任何一个噪声来源的贡献如果大于1 nrad/·Hz1/2,系统相位噪声测量结果均不可能达到该指标;时钟频率抖动与时钟频率的比值为相位噪声[55],当时钟选择10 MHz时,必须满足其相位噪声不高于—175 dBc/·Hz1/2(或时域周期抖动在2 fs 以内);电压幅度噪声对相位噪声测量结果的影响近似呈线性[56],在电压噪声是20 nV·Hz1/2时,需要让测量电压的幅值超过20 V,才有可能获得1 nrad/·Hz1/2的相位噪声,此时动态范围也达到180 dB;相位噪声受量化噪声影响程度取决于模数转换器的位宽和采样率[57],当采样率为5 GSa/s 时,要达到1 nrad·Hz1/2的相位噪声测量结果,位宽应不少于14 bits.

4 典型应用

4.1 光谱增强

因为锁相放大器具有强大的噪声抑制和信号提取性能,最直接最常见的应用即光谱信噪比增强.锁相放大器与精密测量光路的耦合,比较常见的有斩波调制与电开关调制两种,分别如图11(a)与图11(b)所示: 斩波调制使用机械叶轮对光路的周期性遮挡进行光信号有无的切换,由于机械转动频率较低,即使采用多叶轮,调制频率也不超过10 kHz[58,59];当光源部分的控制光,能通过高速半导体器件耦合进光路系统,即可实现1 MHz 以上的高速调制,配置宽带锁相放大器,同样的测量时间内可实现20 dB 的信噪比提升[59-61].随着锁相放大器应用带宽的进一步提升,日本Tanaka 研究组[62]近期报道了一种不同于这两类调制的信噪比增强新方案,利用超快激光的80 MHz 重复频率,通过二分频技术,在40 MHz 频率上直接锁定,从而让太赫兹时域光谱在微秒的响应时间里实现更大的信噪比增强.

图11 锁相放大器用于光谱信噪比增强的两种光路图 (a)斩波器调制;(b)高速电控开关Fig.11.Lock-in amplifier is used to enhance the spectral signal-to-noise ratio in optical measurement via two kind of modulations:(a) Chopper modulation;(b) high speed electronic control switch.

在不同的细分光谱类型中,锁相放大器通常都可以实现信噪比的增强: 为了突破超快时间尺度上锁相探测的难题,北卡罗纳多州立大学的Gundogdu 研究组[63]针对吸收光谱仪的应用场景,结合峰值整形模拟前端电路设计,提出了一种瞬态锁相检测系统,实验证明可将吸收光谱的灵敏度带来数量级的提升;德国明斯特大学的Brenker 研究组[64]介绍了一种将多通道锁相放大器用于膜电位和离子荧光探针的各种组合,可用于多路检测,结合光电倍增管进行弱荧光的锁相并行检测多细胞信号,以毫秒时间分辨率同时记录多个光电探针信号,实现细胞信号通路的原位动态监测;借助锁相放大器对噪声干扰的抑制,靶标含量极低生物样品的微弱发光信号也能被准确提取,从而有望用于更快更灵敏的核酸检测部件[65].在环境监测应用中,来自意大利罗马大学的Sarra 等[66]报道将双通道锁相放大器用于激光透射光谱检测,来实现单分散和多分散纳米颗粒的尺寸和浓度的快速测量,结合可变增益光谱校准方法能将颗粒度分析不确定度降低1 个数量级,这给环境中生物团聚体检测提供了先进的手段.

4.2 阻抗分析

多种物理量信号的矢量组合,可以测得新物理量,由电压与电流信号相除进行频率响应阻抗分析的原理即基于此.将锁相放大器跟电桥结合,同时用于交流电压电流测量,即给交流阻抗分析提供了一种高精度的工具,阻抗分析通常由交流电压与交流电流的比值来进行测量,相比直流电阻测量,该方法能够消除寄生电势的干扰、降低1/f噪声影响,而且还能够有效摆脱直流电表自身的漂移,因而具有明显的优越性,故而在电化学中已经成为一种成熟的方法,在腐蚀、电镀、电解、电催化等反应体系中,用于研究电荷输运、化学传质、离子迁移、界面充放电等过程规律[7].

交流阻抗是锁相放大器的一个主要应用方向,尽管锁相放大器与精密电桥等部件已经被集成在专门的阻抗分析仪中,锁相放大器用户在没有阻抗分析仪的情况下,除了可以通过增加电桥电路来替代阻抗分析仪的功能,还能够在应用锁相放大器与电桥的组合过程中完成普通的阻抗分析仪不能实现的阻抗测量,比如通过极小驱动电流精细测量易烧损器件[67]、在短时间内用较大电流来测量微欧姆及以下电阻[68]、实时反馈补偿与快速成像等[69].

借助锁相放大器进行阻抗分析的4 类典型应用电路如图12 所示.电池内阻测量,锁相放大器技术被应用于储能电池健康监测应用,能有效提高微弱信号检测中的信噪比和分辨率,邓荣与江国栋[70]运用锁相放大器结合交流比例法,实现蓄电池内阻的精确测量(电阻分辨率达17 μΩ),还可以对运行中的电动汽车电池进行精密的在线监测管理[71];生物阻抗分析[72,73];纳米孔阻抗分析[74];超导电阻测量中,交流I-V测量的是直流I-V曲线的一阶导数,反应微分导纳或阻抗性质,通过交直流耦合器件,可以改变或扫描直流偏压来测量微分阻抗随偏压的变化曲线,进而得到比直流电阻测量结果更精确的I-V曲线[75].此外,为了获得纳欧姆级别低损耗元件的准确测量,除了使用无感电阻进行电流监测外,往往还需要进行原位相位补偿[68];精密电容检测,如意大利米兰技术学院的Carminati[76]通过CMOS 超低噪声和宽带电流传感电路耦合到锁相放大器,在1 MHz 范围内进行精密阻抗测量,在极其紧凑的芯片中,通过微米线性位移转换为1×10-18F 的电容步长,对 5×10-21F 的电容分辨率极限进行了理论分析和验证.

图12 运用锁相放大器进行阻抗测量的几种典型场景电路 (a)电池内阻测量[70];(b)生物电阻抗在微流控中监测运动[72];(c)超导电阻测量[68];(d)精密电容监控[76]Fig.12.Several typical application scenes with circuits for impedance measurement using Lock-in amplifier: (a) Battery internal resistance measurement[70];(b) bioimpedance for movement monitoring in microfluidic channels[72];(c) superconducting resistance measurement[68];(d) precision capacitor monitoring[76].

在应用锁相放大器进行交流阻抗测量过程中,应当注意校准和抑制同频干扰[67],还应在频率增加到1 MHz 以上时,考虑电桥欠平衡的问题,在需要时进行非零位电桥的实时监测和扣除[77].

4.3 磁性测量

磁性一般指物质在磁场作用下磁矩等物理量响应的性质,故而其测量不仅包括磁场与磁矩的测量,还包括与磁场相关的耦合物理量的测量.为了获得精密的磁性测量结果,锁相放大器在磁性测量中通常举足轻重,几类涉及锁相放大器的磁性测量方案如图13 所示,分别介绍如下.

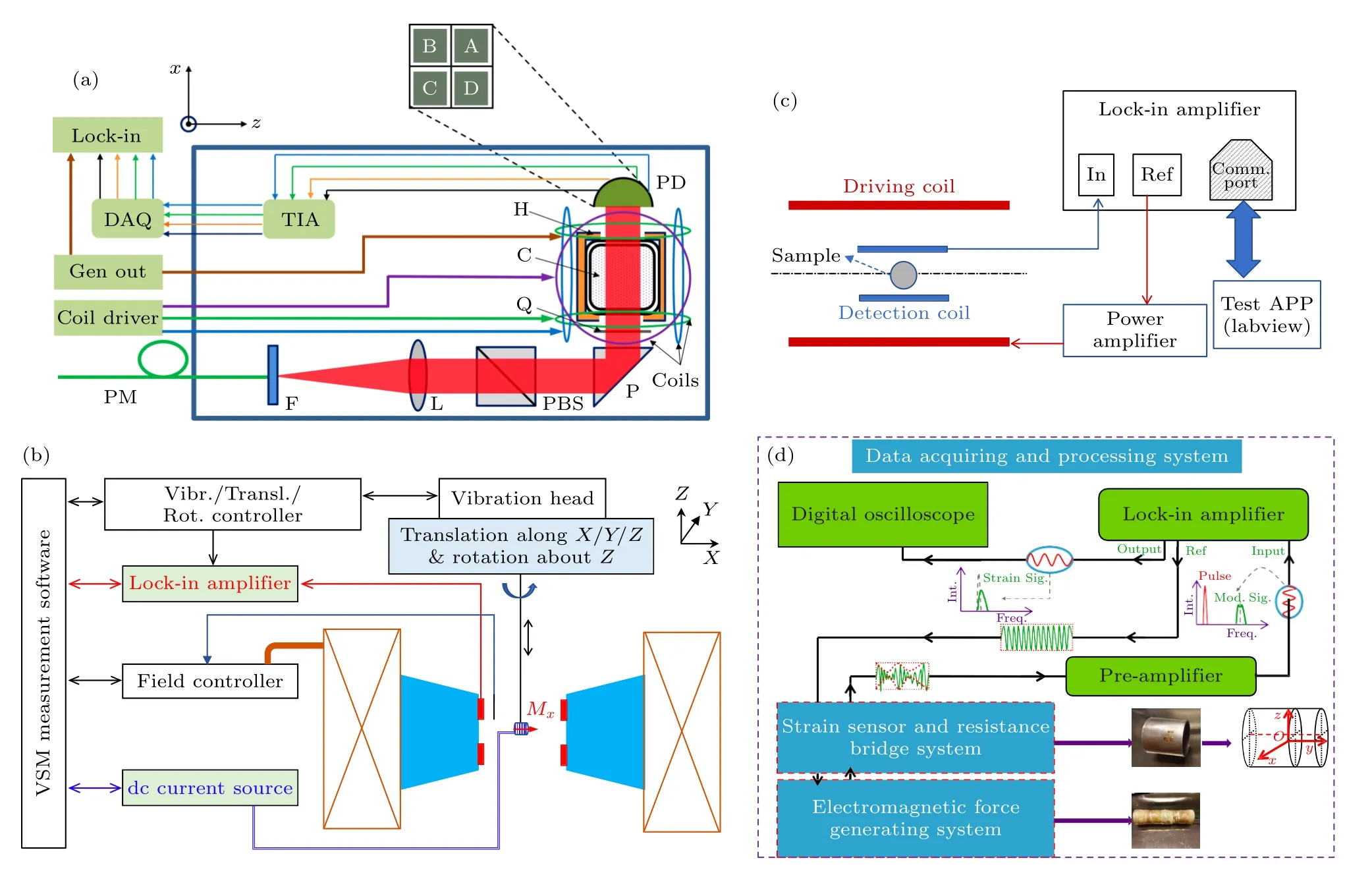
图13 几种典型应用锁相放大器开展的磁测量场景示意图 (a)基于原子磁共振的磁强计[79];(b)振动样品磁强计测量直流磁矩[83];(c)交流磁化率仪;(d)动态磁致伸缩测量[85]Fig.13.Schematic diagrams of typical magnetic measurements carried out by lock-in amplifier: (a) Magnetometer based on atomic magnetic resonance[79];(b) the vibrating sample magnetometer measures the DC magnetic moment[83];(c) AC magnetic susceptibility measurement;(d) dynamic magnetostriction measurement[85].

磁场传感,如图13(a)所示,在极弱磁场的测量方案中,在运用锁相放大器进行原子磁共振信号增强后,无自旋交换弛豫的原子磁强计不仅可以实现0.26 fT·Hz1/2的先进指标[78],还能够小型化到手心尺寸[79].

交流磁化率,如图13(b)所示,经过标定和补偿的互感线圈在插入磁性材料后,用锁相放大器能够灵敏提取磁矩随磁场的变化率信号,从而实现磁化率测量,早在20 世纪80 年代,中国科学院物理所詹文山研究员[80]开始将锁相放大器应用于交流磁化率测量,在低温恒温器中取得0.3 µemu 以下的分辨率并表征了铁基非晶带材的自旋玻璃转变特性[80],近期有日本的研究组用磁性纳米颗粒的磁化率对细菌数目进行定量检测[81].在有些应用场景中,相对于磁化率的绝对测量,用户更关心磁化率的不均匀分布带来的感应变化,从而获得磁性颗粒物的识别与定位[82].

直流磁矩测量最常见的设备是振动样品磁强计,如图13(c)所示,其中探测线圈在载磁矩样品进行振动时感应出交变电压信号,锁相放大器对振动频率下的感应信号进行解调,获得磁矩信息,并可以通过电流线圈的准确标定在较宽的磁矩范围内达到千分之三的不确定度[83].不过,对 1×10-7emu以下的磁矩难以用振动样品磁强计测量,在同级别的成本下,也同样把锁相放大器作为主要部件,交变梯度磁强计是非常好的替代方案.与振动样品磁强计的微弱信号检测原理稍有不同,交变梯度磁强计让磁场梯度线圈快速驱动样品振动,并用锁相放大器来测量该微小高频振动,通过悬臂梁等共振结构设计,让灵敏度显著提升,理想情况下能实现1×10-11emu 的磁矩测量[84].

耦合磁性,如图13(d)所示的磁致伸缩测量方案,通过锁相放大器对应变电阻的高频解调,能够实现脉冲强磁场干扰下,磁致伸缩信号的快速精确测量[85].当然,除了应变片,磁致伸缩的有效测量方案,还可以通过将被测材料跟光纤耦合在一起,施加磁场通过光纤的应变来获得磁致伸缩系数,此时同样离不开锁相放大器对激光干涉相位信号的解调来进行应变的精确测量[86].磁致伸缩以外的耦合磁性,也通常离不开锁相放大器进行微弱磁耦合信号的增强和提取,比如磁光克尔效应[87]、磁电耦合效应[25]、磁阻抗效应[88].

在磁性测量过程中,一方面由于磁性材料的磁化曲线本身的非线性,另一方面设计的探测线圈灵敏度受样品位置影响较大,磁性信号的输出相比输入存在明显的非线性,这种非线性符合傅里叶级数展开规律,因而可以用倍频或高次谐波的测量技术进行表征,高次谐波测量可以在较短时间里对非线性信号进行定量挖掘,因而经常被用在交流磁化率仪[89]、高灵敏振动样品磁强计[90]等仪器中.

4.4 显微成像

显微成像是科学研究走向微观探索未知的必经之路,其中颇具代表性的原子力显微镜中,锁相放大器是必不可少的部件[91].为了获得稳定清晰的原子级别图象,锁相放大器跟探针之间不仅需要高品质因子的悬臂梁对微弱信号增强,还需要高速低噪声位移反馈[92],其闭环测控结构示意如图14(a)所示.

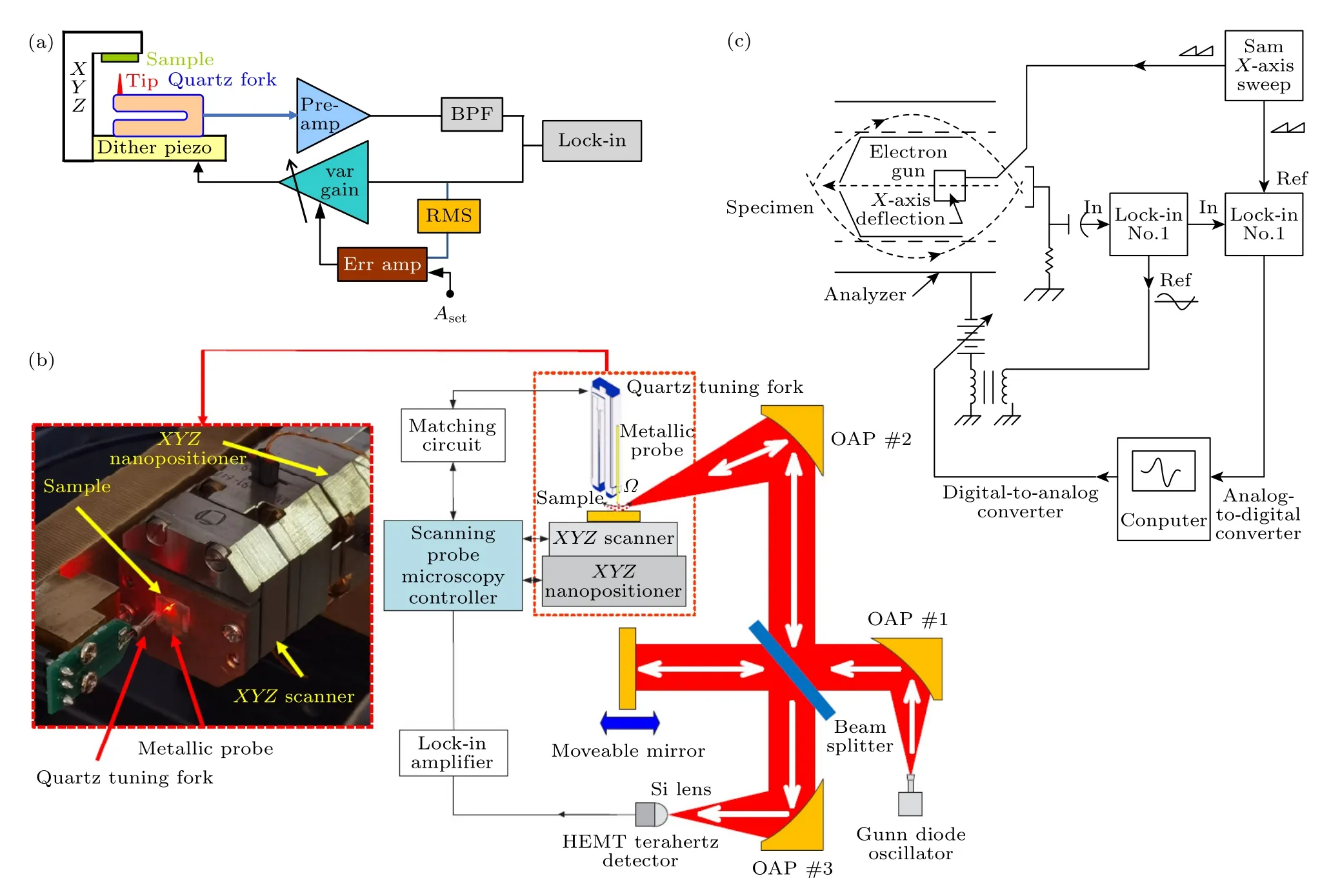
图14 几种用到锁相放大器的显微成像系统 (a)原子力显微镜[92];(b)近场光谱显微镜[94];(c)扫描俄歇电子显微镜[95]Fig.14.Several microscopic imaging systems using lock-in amplifier: (a) Atomic force microscopy[92];(b) near field spectroscopic microscope[94];(c) scanning Auger electron microscope[95].

原子力显微镜和激光光路耦合后,可以同时获得样品的形貌和近场光学成像.利用探针与样品在光场下产生的近场相互作用,可以实现20 nm 左右分辨的光学成像[93].相关仪器结构如图14(b)所示,入射激光被聚焦到表面镀层为金属的探针尖端,因为尖端极化电荷的动态束缚效应增强了探针下方的电磁场,从而改变了探针表面的极化电荷分布,同时探针又具有光学天线的作用,向自由空间辐射电磁场,从而将针尖与光场相互作用转换为被探测器接收的散射信号,进而获得高空间分辨的近场微波成像[94].

图14(c)展示了锁相放大器用在扫描电子显微镜中的结构,这里俄歇微探针上引入样品表面电荷调制或束斑扫描位置调制,可以抑制光束漂移带来的影响,从而实现微弱二次电子信号的高信噪比成像[95].

4.5 空间探测

在空天探索领域,空间引力波探测是当前国际研究热点,其核心技术是测量相距数百万千米的两测试质量间的平动转动等相对运动,激光外差干涉是实现如此远距离的两个物体之间精密测量的有效方法,这里必须通过锁相装置对相位信号跟踪分析,方能实现对引力波的测量[96].跟锁相密切相关的激光外差干涉中最常用的两种测试光路——单一激光源双光束与主从双激光源跟踪分别如图15(a)与图15(b)所示.单一激光源产生的双光束相干性好,通过声光调制又能将双光束的相位差频移到设定的水平[54];主从式激光源与单一光源产生的双光束相比,需要从光束合路干涉信号中提取出较大范围的频差信号,被用于从激光器腔长的精细调节,来达到跟主激光器的相位跟踪.主从式相位跟踪看起来稍微复杂些,但对于远距离空间探测必须的中继来说将是非常可行的方案,此时主激光器的光束可能强度较弱,但经过同相位跟踪与再生,即可让探测信噪比得到提升.

图15 激光外差干涉采取的两种运用锁相反馈的光路 (a)单激光源输出相位可控的一对激光束;(b)主从双激光源输出一对激光束Fig.15.Laser heterodyne interference two optical paths using phase-locked feedback: (a) A pair of laser beams with controllable phase coherence from a single Laser;(b) the master-slave dual light source outputs a pair of laser beams.

相位严格可控的双光束除了开展如引力波验证的远距离空间探测,同样的光源被用于二维光谱提取[97],以及通过光频梳实现kHz 级别精度的太赫兹光谱[98],即可实现分子指纹信息的精细测量,其中,光谱要求得越精细,对锁相的要求就也越高.

空间探测应用的锁相放大器,通常被应用为相位计,在这种应用中,由于需要获取平动转动等多自由度信息,同时要顾及激光测量过程中的较大范围频率漂移,使得锁相放大器不仅需要具有10 MHz以上的带宽、多达16 以上的通道数,而且跟通常锁相放大器的相位测量只限于0—360°内输出不一样,相位计中的相位输出范围超过10 亿度,以满足较大距离内的准确跟踪[96].

4.6 新型应用

除了前述主要应用方向,锁相放大器近些年还被用于一些新的场景,本节进行汇总简介.

在大科学装置中,印度空间应用中心的Priya小组[99]通过使用“粗-细”协调双数模控制器组合的思路设计,以获得高分辨率的控制电压输出,粗和细DAC 之间有一些重叠,从而让铷原子钟结合ALIA,获得1000 s 时间内 1×10-14量级的相对不确定性.德国亚琛工业大学等单位在加速器和储能环装置中,用锁相放大器作为关键部件的离子速度选择器,以接近量子不确定性原理极限的精度,在单个粒子上的最小洛伦兹力10 aN 的估测[100].

锁相放大器在以多种方式尝试改进智能计算的性能.锁相放大器的精密测量和反馈特性在高性能计算中的作用也开始显露.量子计算机模拟实验中,锁相放大器也是对每个量子比特进行单独操控的有效工具[101].将精密测量与实体电路协同融合,可以形成电磁反演的硬件解决方案: 经验证该方法对于电阻、电容、电感等无源器件构成的网络能够以0.1%的准确度进行定量反演,可重构电路网络还能调整自身的拓扑结构以适应复杂的反演任务.新的反演方案用原始的测量数据通过测量与重构协同的方式建立从物理世界到物理世界的自动直接反演,中间无需数值空间过渡,从而将O(N·N)复杂度降低成O(N)复杂度,实现高效的电磁反演,未来有望集成为即刻处理反演芯片[102].随着模拟比特单元的测控技术不断成熟,不难预测,未来的智能计算机将会较大规模地融合模拟测控和数字逻辑.亚利桑那大学Jung 博士[103]提到利用锁相技术生成的像素时钟,对输入影像的RGB 分量信号分别进行去噪声处理并恢复成高清图象,以供高分辨数字显示.锁相放大器算法可应用于比如人脸表情等多维度社会学数据的精细挖掘,并通过研究人脸表情对美感知时心理状态的定量评估,结果表明在相当大的干扰情况下,锁相放大及反馈算法也可以对心理状态变化进行指示[104].

近些年,锁相放大器从常规仪器演变到电路板模块乃至芯片,从而应用于精准物联网与工业快检等领域.尽管以前电力电工中的精密测量未见被关注,近年来,锁相放大器已经被用于电网中精密的相位测控与功率分析[105,106].奥地利的Neunteufel团队[107]通过锁相环固件更新实现了宽带信号生成,提出窄带物联网收发器芯片上定制宽带调制方案用于室内定位,并在一家杂货店的真实环境下,用2.4 GHz 带宽实现了1200 多个节点定位精度约2.2 m 的测试,验证了应用可行性.为了适应新的大规模应用趋势,降低锁相放大器成本和降低功耗,延长其持续工作时间,西班牙Zaragoza 大学的Celma 研究组[108]研发和传感器联用的5 mW低功耗集成锁相电路,在—24 dB 的信噪比下能够获得6%以内的误差.

5 结语

对信号进行相位锁定的技术从诞生至今不足百年,却经过收音机与电视到宽带通信及万物互联的进化过程,并不断发展,帮助人类越来越精细地感知与运用自然界,作用举足轻重.锁相放大器经历了从模拟到数字直至虚拟的技术演化,幅度、频率与相位噪声等锁相放大器性能的检测方法也日趋成熟.随着锁相技术在电、磁、光、声等物理过程,以及从微观到宏观的深入应用,其结构与性能将会通过先进科学仪器的研发和应用进一步创新和升级.在满足工业需求的前提下进一步降低成本,锁相放大器均会被更加广泛应用;此外,随着包括量子计算机在内的模拟计算技术的兴起,不难看出锁相放大器也会以更高集成度的形式进入每个人的智能终端.