基于色散光学模型的40Ca 核子散射数据计算

赵岫鸟 杜文青

(渤海大学物理科学与技术学院,锦州 121013)

对钙同位素核数据的研究具有重要的理论价值和应用前景,其中40Ca 作为天然钙最主要的同位素,是一种重要的材料核素.本文采用色散光学模型对球形核40Ca 的核子弹性散射数据进行计算.通过考虑色散光学模型势中实部势的非定域性以及虚部势的壳间隙结构,实现了对40Ca 相关核子散射数据的良好描述,其中包括中子总截面、核子弹性散射角分布以及分析本领.此外,本文计算了色散光学模型势的实部体积分,其随能量的变化图像在费米能附近出现了明显的色散峰结构.

1 引言

钙作为一种重要的材料核素,被广泛应用于制备镁钙合金、铝钙合金以及硅钙合金等合金材料.在镁钙合金中,钙核因其可以提高镁合金材料的可轧制性并降低材料的微电池效应,从而使镁钙合金材料被成功地应用在航空航天、电子通信、汽车制造等领域.在铝钙合金和硅钙合金中,由于钙核对氧以及硫具有很强的亲和力,相关合金可以作为复合脱氧剂、脱硫剂,被应用于优质钢、镍基合金、钛基合金等合金材料的生产中.随着核工程应用需求的扩大,相关应用对钙核的基础核数据提出了更高的精密化要求.其中,40Ca 作为钙的5 个稳定天然同位素中最稳定的核素,其丰度占天然钙的96%以上,对40Ca 核子散射数据的研究和计算具有较高的理论价值和应用前景.

对核子散射数据的研究和计算通常采用光学模型,其中光学势作为光学模型的核心内容,在相关研究中取得长足发展[1].特别地,出于因果关系的要求,即散射波不会在入射波到达之前射出,在核子散射问题的相关研究和计算中需要考虑色散效应.自从Mahaux 和Sartor[2]提出可以利用色散关系联结光学势的实部和虚部并实现平均场从正能外推到负能以来,随之发展的色散光学模型(DOM)得到广泛的应用,并取得了大量的成果[3–9].不同于传统光学模型(如Koning-Delaroche 光学势)研究中需要通过在光学势中额外添加独立的色散项来考虑色散效应,该模型通过引入色散关系将色散贡献自洽地添加到光学势中.色散关系的引入,使光学势的实部势和虚部势相互联系,在一定程度上提升了模型的科学性并减少了相关参数的数量.近期,以Dickhoff 和Charity[10]为首的研究人员采用DOM 对幻数核和近幻数核的核子散射问题进行了研究.结果发现,费米能以上和费米能以下的体虚部势深度并非完全对称,而是随着核子入射能量的增大呈现出明显的非对称形式.因此采用非对称形式的体虚部势可以改善模型对入射粒子能量远离费米能时的散射数据的描述.

我们曾采用并发展了一套与Lane 方程自洽的唯象色散光学势,通过引入同位旋矢量项,实现了用同一光学势对中子、质子散射数据进行描述,并且对体虚部势进行了高能修正,合理地考虑了体虚部势的非对称性,从而实现了对入射能远离费米能时的散射数据的良好描述[11].此外,我们还考虑了实部势的非定域性以及虚部势在费米能附近的壳间隙结构,从而使色散光学势得到了进一步的改进[12,13].考虑到40Ca 在费米能附近具有明显的壳间隙结构,因此本工作将进一步检测改进后的DOM 对40Ca 核子散射数据的计算情况.

为更好地实现对双幻数核40Ca 核子散射数据的高精度描述,本文采用与文献[12]类似的方法,旨在得到一套考虑光学势实部的非定域性以及虚部壳间隙的色散光学势及其参数,从而实现对40Ca 核子散射数据(包括中子总截面、核子弹性散射角分布以及分析本领)的良好描述.

2 色散光学势

对于双幻数核40Ca,采用DOM 对其进行描述,色散光学势包含实部势VHF(E)势(即Hartree-Fock (HF)项),体(v)虚部势、表面(s)虚部势、自旋-轨道耦合(so)实部和虚部势,以及相应的色散修正项ΔVv(E),ΔVs(E)和ΔVso(E).采用的色散光学势的具体形式如下:

式中E*表征核子的有效能量,对于中子入射,E*=En;对于质子入射,E*=Ep-ECoul=Ep-其中,En和Ep分别代表中子和质子的入射能量,Z和Z′分别代表入射核子和靶核的电荷数,A为靶核的质量数,CCoul为可调参数.

光学势中采用Woods-Saxon 形式的形状因子,具体表达式为

实部势VHF(r,r′) 被认为具有高斯形式的空间非定域形式[14]:

其中参数β 表征非定域性的范围.将这种形式的非定域势[14]进行定域近似,可以得到如下隐式方程:

(5)式可以被显性表示为

其中λ≡µβ2/(ℏc)2,AHF为同位旋矢量项((12)式).体虚部势Wv,表面虚部势Ws,自旋-轨道耦合势Vso和Wso的能量依赖关系分别参考Brown和Rho[15],Delaroche 等[16]和Koning 等[1]的相关研究.同时依照Molina 等[17]的建议,本文在DOM 势的虚部势中引入壳间隙Δ,光学势中各虚部势的具体形式如下:

其中Av,Bv,Bs,Cs,Wso和Bso均为可 调参数,As为同位旋矢量项((13)式).由于双幻数核在费米能附近存在明显的单粒子能级结构和较大的能级间隙,在该能级间隙内没有能级分布,故不存在粒子布居.因此我们在光学势的虚部势中引入壳间隙结构,假设在费米能EF附近宽度为Δ=2(EPEF)的区域内虚部为0.需要注意的是,对于中子和质子散射EP和EF是不同的.费米能以下的虚部势通过对称条件W(2EF-E)=W(E) 来定 义.对 于体虚部势,仅当核子入射能量在 |E-EF|＜Ea的能量范围内保持对称形式; |E-EF|＞Ea时,根据Mahaux 和Sartor 的相关研究[18]对体虚部势进行如下修正:

特别地,在实部势VHF和表面虚部势Ws中引入了同位旋矢量项(即Lane 项[19,20]):

其中V0,Cviso,W0和Cwiso为待定参数.光学势(1)式中实部除了Hartree-Fock项VHF(E) 势和自旋-轨道耦合势实部势Vso(E) 之外,还包含了三项色散修正项,即体色散修正项 ΔVv,表面色散修正项 ΔVs和自旋-轨道耦合色散修正项 ΔVso.各个色散修正项均由相应的虚部势通过色散关系引入,色散关系的具体形式如下:

其中P表示应取该积分的主值.光学势(1)式中最后一项VCoul为库仑势,只存在于质子入射的情况.

调节色散光学势参数使目标函数χ2达到最小,从而得到“最优参数”[21].目标函数χ2的具体表达形式如下:

其中,dσ/dΩ与σtot分别表示角分布数据和总截面数据,上标“cal”和“exp”分别代表计算值和实验值.本文使用的所有实验数据均取自EXFOR 实验数据库[22].表1 列出了本文得到的色散光学势参数;图1 给出了相应的DOM 势各项势深度随能量的变化情况.

图1 40Ca 中子诱发核反应计算中,光学势各项深度随能量的变化情况Fig.1.Energy dependence of the DOM potential depths calculated for neutron induced reactions on 40Ca.

表1 40Ca 中子诱发核反应计算中的DOM 势参数Table 1.DOM potential parameters for nucleon induced reactions on 40Ca.

3 结果及分析

图2 为计算得到的中子总截面与Koning-Delaroche (K-D)光学势给出的计算结果以及实验数据的比较情况(本工作比较的K-D 光学势为RIPL 库中针对40Ca 单独调参后的光学势).可以看出,本工作实现了在较大的核子入射能量区间(100 keV—200 MeV)上对中子诱发核反应总截面的良好描述,与K-D 光学势给出的描述情况类似.随着中子入射能量的降低,实验数据表现出明显的共振结构.唯象光学模型势本身只能给出平滑的计算结果,无法给出总截面在共振区间具体的振荡形式.在入射能量小于6 MeV 时,我们给出的计算结果与实验数据的平均趋势较为吻合.当中子入射能在10 MeV 左右时,对总截面的计算结果略微偏低.除了受到参数选取的不确定性的影响外,虚部势在附近能区发生迅速的变化,要改进该区域内对相关数据的描述质量,需要进一步对虚部势的非定域性进行更细致的考虑.

图2 40Ca 的中子总截面计算结果与K-D 光学势给出的计算结果以及相关实验数据的比较Fig.2.Comparison of the calculated total cross section for 40Ca with calculations using the K-D potential and measurements.

对40Ca 的中子和质子弹性散射角分布的计算结果如图3 和图4 所示,与实验数据拟合较好,对中子弹性散射角分布数据的描述质量与K-D 光学势类似,对质子入射能量较大时的弹性散射角分布数据的描述质量稍优于K-D 光学势.

图4 40Ca 的质子弹性散射角分布计算结果与K-D 光学势给出的计算结果以及相关实验数据的比较Fig.4.Comparison of proton elastic scattering angular distributions for 40Ca with calculations using the K-D potential and measurements.

图5 和图6 给出了对40Ca 的中子和质子弹性散射分析本领的计算情况.可以看出本工作对分析本领有着较好的描述,描述质量与K-D 光学势给出的结果相似,计算结果与实验数据吻合得较好.

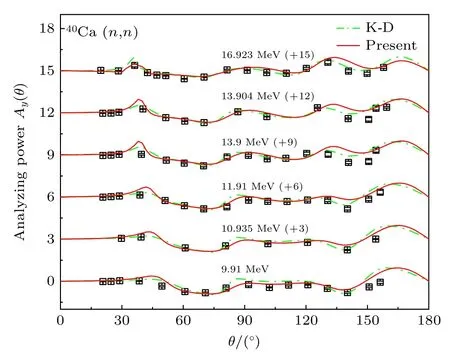
图5 40Ca 的中子 弹性散 射分析 本领计算结果 与K-D 光学势给出的计算结果以及相关实验数据的比较Fig.5.Neutron elastic scattering analyzing powers for 40Ca compared with calculations using the K-D potential and the experimental data.

图6 40Ca 的质子 弹性散 射分析 本领计算结果 与K-D 光学势给出的计算结果以及相关实验数据的比较Fig.6.Proton elastic scattering analyzing powers for 40Ca compared with calculations using the K-D potential and the experimental data.

由于各种散射截面的计算与光学势各项的体积分密切相关,我们给出了DOM 势中实部势体积分随能量的变化情况.如图7 所示,由于色散修正项的引入,总的实部势在费米能附近出现了明显的“色散峰”.在没有引入色散关系的光学模型中需要通过采用与能量相关的几何参数才能得到与DOM势相似的体积分随能量的变化情况.在本工作中,DOM 势通过色散关系自洽地获得实部体积分的色散峰结构,从而使光学势的几何参数能够摆脱对能量的依赖关系.

图7 40Ca 的中子诱发核反应计算中DOM 势实部体积分随能量的变化情况,其中右边纵坐标度量 VHF 势和总的实部势,左边纵坐标度量色散修正项Fig.7.Energy dependencies of calculated real volume integrals of dispersive optical model potential for neutron induced reactions on 40Ca.Volume integrals of and total real potential by using right Y-axis,the volume integrals of dispersive terms by using left Y-axis.

4 结论

我们分析并采用先进的DOM 对40Ca的核子散射数据进行了计算.相应的色散光学势中引入了色散关系、同位旋相关项以及对体虚部势的高能修正,并且考虑了VHF势的非定域性,同时在虚部势中引入了壳间隙,进而实现了对包括中子总截面、弹性散射角分布以及分析本领在内的40Ca的中子、质子散射数据的良好描述.