基于联邦模型迁移的不同规格滚动轴承故障诊断方法
2023-12-01康守强王玉静王庆岩梁欣涛Mikulovich
康守强, 肖 杨, 王玉静, 王庆岩, 梁欣涛, V.I. Mikulovich
(1.哈尔滨理工大学 测控技术与通信工程学院,哈尔滨 150080;2.白俄罗斯国立大学,明斯克 220030)
滚动轴承作为旋转机械关键部件之一,广泛应用于工业生产中,对其及时进行故障诊断可有效防止重大事故发生[1]。实际工程中,滚动轴承通常工作于复杂、恶劣的环境中或拆卸困难,导致某些规格滚动轴承振动数据稀缺,尤其是带标签数据[2]。同时,由于不同规格的滚动轴承振动信号往往存在较大的数据分布差异,若将其直接用于其他规格滚动轴承故障诊断,会导致误诊断的概率增大。因此,通过某种规格滚动轴承的先验知识,建立其他规格滚动轴承故障诊断模型具有重要意义。
近年来,深度学习凭借其强大的自适应提取特征能力,被广泛应用于轴承故障诊断领域[3]。文献[4]提出一种改进的残差网络,将SENet引入到深度残差网络中,实现滚动轴承故障诊断。文献[5]采用一维卷积神经网络对航空发动机轴承故障进行分类,具有较高的诊断准确率。文献[6]提出一种改进的SqueezeNet模型,采用3个3×3卷积核代替1个7×7卷积核,并利用直升机轴承振动数据证明其方法的有效性。文献[7]利用不同尺度的一维卷积核提取原始振动信号的多尺度特征,通过对多层网络学习实现滚动轴承故障诊断。文献[8]利用一维和二维卷积神经网络提取特征并构建新的时频特征,成功应用于机车轴承故障诊断。
基于深度学习的故障诊断方法在模型训练过程中通常需要大量已知标签样本集。某些规格轴承在实际工作中,由于拆卸不便、振动信号采集困难,导致已知标签样本数量稀缺,建立的故障诊断模型难以达到理想效果。
针对深度学习故障诊断方法存在的问题,众多学者将研究重点转移至迁移学习领域,其目的是将某个任务的已知知识应用到相似任务中。文献[9]针对海水泵工况复杂多变、故障数据采集困难等问题,提出一种基于参数迁移的故障诊断方法,并在3个海水泵数据集上验证了方法的有效性。文献[10]提出一种改进的迁移学习方法,使用全局均值池化层对轴承故障分类,实现了少数据情况下滚动轴承故障诊断。文献[11]使用格拉姆角差场将一维振动信号转变为二维故障图后,利用模型迁移学习方法进行轴承故障诊断,其方法具有较高的诊断准确率。文献[12]使用源域数据训练改进的卷积神经网络,将模型参数迁移至目标域网络并微调,利用公共轴承数据集验证其有效性。文献[13]提出4种将原始振动信号转变为图像样本的方法,并使用迁移学习方法实现含噪声条件下轴承故障诊断。文献[14]提出一种改进的无监督域适应诊断方法,通过仿真数据构建源域,并设计一种改进的损失函数,最后使用2个数据集验证了其方法的可行性。
然而,随着数据安全问题逐渐受到关注,世界各国政府纷纷颁布多条相关法律以加大数据隐私管理力度。2016年欧盟出台的《通用数据保护条例》和2018年美国颁布的《加州消费者隐私法案》都有强调保护个人隐私数据。我国于2021年颁布的《个人信息保护法》中也明确指出,处理个人信息应当取得个人同意。同时,用户由于数据隐私问题不希望共享私有的轴承振动数据,振动数据通常以孤岛形式存在多个用户中,无法汇聚成大数据。因此,基于迁移学习的轴承故障诊断方法存在源域缺乏大量先验知识,而构建源域预训练模型困难的问题。
联邦学习是基于上述背景提出的一种分布式机器学习方法,作为人工智能领域的一个重大突破,根据“数据可用不可见,数据不动模型动”的思想,旨在联合多方数据共同建模,打破“数据壁垒”,实现多方“共同富裕”[15]。文献[16]提出一种联邦学习模型聚合过程中的加权策略,提升全局模型的质量,利用轴承数据集验证了所提方法的有效性。文献[17]基于联邦学习设计了一种轴承故障诊断方法,实现了孤岛数据情形下滚动轴承故障诊断。文献[18]提出一种基于联邦学习和卷积神经网络的故障诊断方法,在滚动轴承数据集上具有较高的诊断准确率。文献[19]基于动态路由技术提出一种多工况故障诊断联邦学习系统,并以滚动轴承数据集为基准数据集验证所提方法的优越性。文献[20]在联邦学习框架上提出一种动态验证方案,其目的是提升全局模型对低质量本地数据的鲁棒性,并在轴承和转向架2个数据集上取得良好的诊断效果。
由于不同规格滚动轴承振动数据之间差异较大,直接使用联邦学习方法聚合多个用户不同规格滚动轴承振动数据,易导致模型诊断效果较差;而用户使用本地孤岛数据直接建模会因已知标签数据较少无法建立有效的故障诊断模型。针对上述问题,提出一种基于多用户孤岛隐私数据联邦模型迁移的不同规格滚动轴承故障诊断框架。该方法以联邦模型迁移框架为基础,使用卷积神经网络提取振动信号特征,构建用户本地模型。使用改进的参数策略减少本地模型参数数量,提升参数传递过程的安全性。最终,多个用户协同构建用于迁移学习的共享模型并发送给用户,用户使用本地数据微调共享模型,实现不同规格滚动轴承故障诊断。
1 卷积神经网络
近年来,卷积神经网络(convolutional neural networks,CNN)凭借其良好提取图片特征的能力,受到图像分类、目标识别等各个领域的广泛关注。与传统神经网络相比,卷积神经网络可以通过参数共享、稀疏连接等操作,快速地提取图片特征同时降低模型参数数量,大幅度提升训练速度[21]。常见的卷积神经网络由输入层、卷积层、池化层、全连接层、输出层构成,如图1所示。
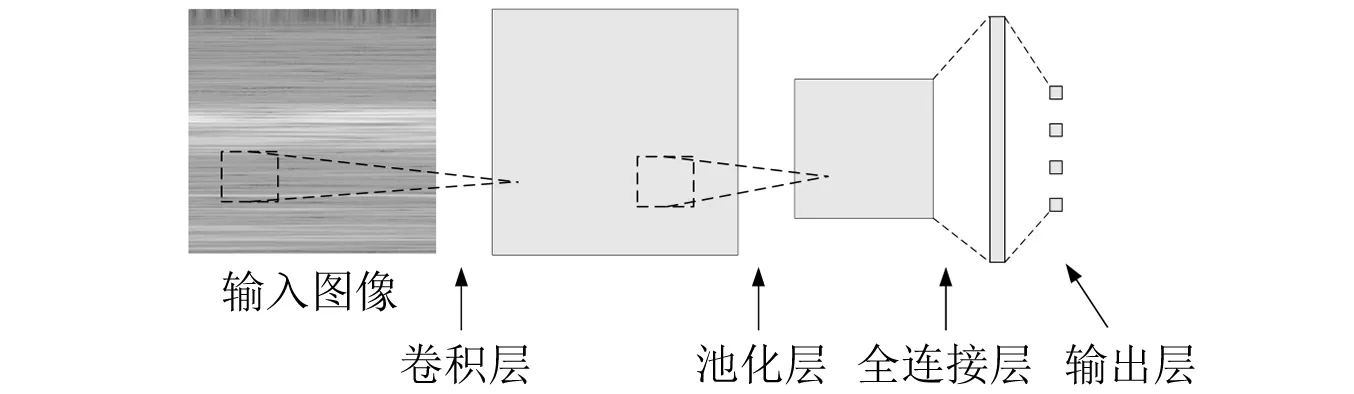
图1 卷积神经网络结构Fig.1 The structure of convolutional neural networks
1.1 卷积层
作为卷积神经网络中最核心的部分,卷积层主要负责提取输入图像的特征。利用预先确定好尺寸的多个卷积核,与输入图片对应区域加权求和,提取图片的局部特征。卷积层提取特征的公式为
(1)
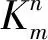
1.2 池化层
池化层在CNN中主要负责对卷积层提取的特征进行降采样操作,保留图片中重要信息的同时减少了网络参数量。常见的池化方法有最大池化和平均池化两种,两种池化方法如图2所示。

图2 池化方法示意图Fig.2 Diagram of pooling method
1.3 全连接层
全连接层通常放置在整个CNN的最后,能够将卷积层提取的局部特征拟合为全局特征,并起到分类的作用。全连接层输出的公式为
h(x)=f(ωx+b)
(2)
式中:x为该全连接层输入数据;ω为权重;b为偏置;f(·)为激活函数;h(x)为该全连接层输出。
2 联邦迁移学习
2.1 联邦学习
联邦学习框架通常由多个用户和聚合服务器构成,且聚合服务器不会泄露用户信息,用户本地数据始终留在本地不共享给其他用户,仅通过共享本地模型参数协同建立一个全局模型。假设有K个用户参与联邦,每个用户的本地数据集为Dk,k=1,2,…,K,则联邦学习建模过程如下。
首先,所有的建模任务都可以视作对损失函数的优化过程,即
min[f(x)]
(3)
式中,f(w)为当前任务的损失函数,w为当前模型参数。
传统中心化模型训练将所有数据集中到一起,则有
(4)
式中:fi(w)为第i个样本的损失;n为数据集样本个数。
不同于传统中心化训练过程,联邦学习不需要集中数据,则联邦学习优化目标函数可定义为
(5)
(6)
式中:Fk(w)为联邦学习中第k个用户的损失;nk为第k个用户的样本数。
联邦学习流程框图如图3所示。服务器将全局模型发送至各个用户作为本地模型;用户利用本地数据训练本地模型,并将模型参数上传至服务器;服务器通过聚合算法聚合本地模型参数并更新全局模型后,再次发送给用户。重复上述步骤直至达到最大联邦迭代次数,得到最终的联邦全局模型。
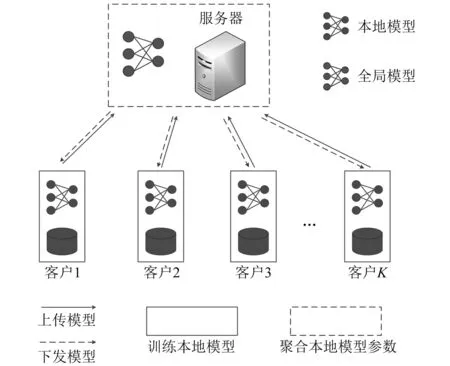
图3 联邦学习流程框图Fig.3 Flow block diagram of federated learning
联邦平均算法作为联邦学习中最常用的模型参数聚合方法,其表达式为
(7)
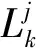
2.2 模型迁移学习
模型迁移学习旨在将源域中训练好的模型参数信息迁移到具有相似任务的目标域中,并利用当前任务已知标签样本集对模型参数微调,使其适应新任务。模型迁移学习之所以能够利用源域先验知识辅助目标域建模达到理想效果,根本原因在于卷积神经网络提取特征具有层次性,浅层网络提取数据共有特征,深层网络提取较为抽象的特征。微调作为模型迁移中常见的调参方法,正是利用共有特征具有普适性的特点,共享浅层网络参数,调整深层网络参数,使源域网络快速适应新任务。
微调的关键是找出不同数据集间的不变量,也就是源域与目标域之间的共性知识,因此本文提出逐层解冻思想对网络微调,具体方法为:将用于迁移学习的共享模型(除全连接层)参数迁移至目标域网络,作为目标域网络的初始化参数,从最后一层卷积层向前逐层解冻,并使用目标域已知标签样本微调网络,参数迁移过程如图4所示。

图4 模型迁移策略Fig.4 Model transfer strategy
2.3 改进参数传递策略
联邦学习无需汇集用户数据,而是通过聚合模型参数协同建模提高模型质量。但仍存在一些问题,即用户不希望自己的私人数据以及本地模型参数被他人获取,一旦出现信息泄露可能导致重大财产损失。因此,联邦学习参数传递过程的安全性是值得研究的重点问题之一。
针对上述问题,引入差值更新策略,通过更新本轮本地模型和上一轮全局模型参数差值的方法实现全局模型参数更新,原参数更新的方法如式(8)所示
(8)
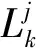
使用差值更新改进后的全局模型更新过程如式(9)所示
(9)
上述式(9)化简后与式(8)是一致的,但参数传递过程中,传递的参数由模型的参数变为了参数差值,若被截获,也无法从中获取到具有实际价值的信息。参数稀疏化算法是通过生成一个与参数矩阵大小相同的由0,1组成的矩阵,再与原参数矩阵对应位置相乘,从而减少参数数量的方法。参数稀疏化度是矩阵中1的个数与0,1个数之和的比值,即90%参数稀疏化度为矩阵中1的个数占90%。基于此思想,本文引入一种参数稀疏化算法改进联邦学习过程中参数传递策略,用于解决用户上传参数时的隐私泄露问题。本文采用的参数稀疏化算法在联邦学习框架中的具体步骤:
步骤1用户使用本地数据训练好本地模型后,按层计算本轮初下发的全局模型参数与本轮训练好的本地模型参数差值,每一层的差值为一个矩阵。
步骤2用户本地生成一个和模型参数同样大小的矩阵,矩阵由0、1组成,1的个数由事先规定好的参数稀疏化度决定。
步骤3将步骤1中得到的差值矩阵与2中生成的参数稀疏化矩阵对应位置相乘得到新的差值矩阵。
步骤4将新的差值矩阵发送给服务器,服务器收集所有用户的差值矩阵取其平均数,加到上一轮的全局模型参数矩阵上,形成下一轮的全局模型。
3 不同规格滚动轴承故障诊断方法
基于联邦模型迁移的不同规格滚动轴承故障诊断方法流程框图,如图5所示。

图5 故障诊断流程框图Fig.5 Fault diagnosis flow diagram
滚动轴承故障诊断方法具体步骤如下:
步骤1本地数据集及本地模型构建
选取不同规格滚动轴承振动数据作为各用户本地数据集,并通过短时傅里叶变换得到用户本地时频图。利用本地时频图样本集训练卷积神经网络得到多个用户本地模型。
步骤2共享模型构建
利用提出的改进参数传递策略,用户将训练好的本地模型参数上传至服务器,服务器使用联邦平均算法聚合用户上传的参数并更新本地模型,不断重复此过程直至达到最大联邦迭代次数,得到用于迁移学习的共享模型。
步骤3个性化模型构建
服务器将用于迁移学习的共享模型发送至各用户,根据提出的逐层解冻策略决定保留共享模型哪些层参数,并使用本地数据集对共享模型微调,得到适用于用户本地数据集的个性化模型。
4 应用与分析
4.1 试验数据集与试验设置
本实验数据来自试验台轴承数据集[22]。轴承数据试验平台如图6所示,试验平台由电动机、扭矩传感器、功率测试计以及电子控制器组成。驱动端为SKF6205规格轴承,风扇端为SKF6203规格轴承,采样频率均为12 kHz,工作在0,0.75 kW,1.50 kW和2.25 kW共4种负载情况下。数据集包含正常、内圈故障、外圈故障和滚动体故障在内的4种状态,轴承故障是在轴承每个部位利用电火花加工而成的点蚀故障,每种故障类型分别有0.177 8 m,0.355 6 m,0.533 4 mm共3种故障缺陷直径,共10种类别。

图6 轴承试验台示意图Fig.6 Schematic diagram of bearing test platform
本文随机截取1 024个连续点作为一个样本,如图7所示。为方便表示各种状态类别,以N代表正常状态,其余9种故障状态具体表示如表1所示。

表1 9种故障状态

图7 时域振动信号截取方式Fig.7 Time domain vibration signal interception method
为更清晰地表示试验中所用到的数据,表2中给出了本文所使用的数据集与轴承规格、工作负载、转速的对应关系。

表2 数据集与轴承规格、负载、转速对应关系
本文设置8组不同的联邦任务,各任务中用户本地数据,如表3所示。以任务1为例,用户1持有SKF6205(0,1 797 r/min)数据,用户2持有SKF6205(1,1 772 r/min)数据,用户3持有SKF6203(0,1 797 r/min)数据。每个用户训练样本每类30个,10个类别共计300个,测试样本每类100个,共计1 000个。
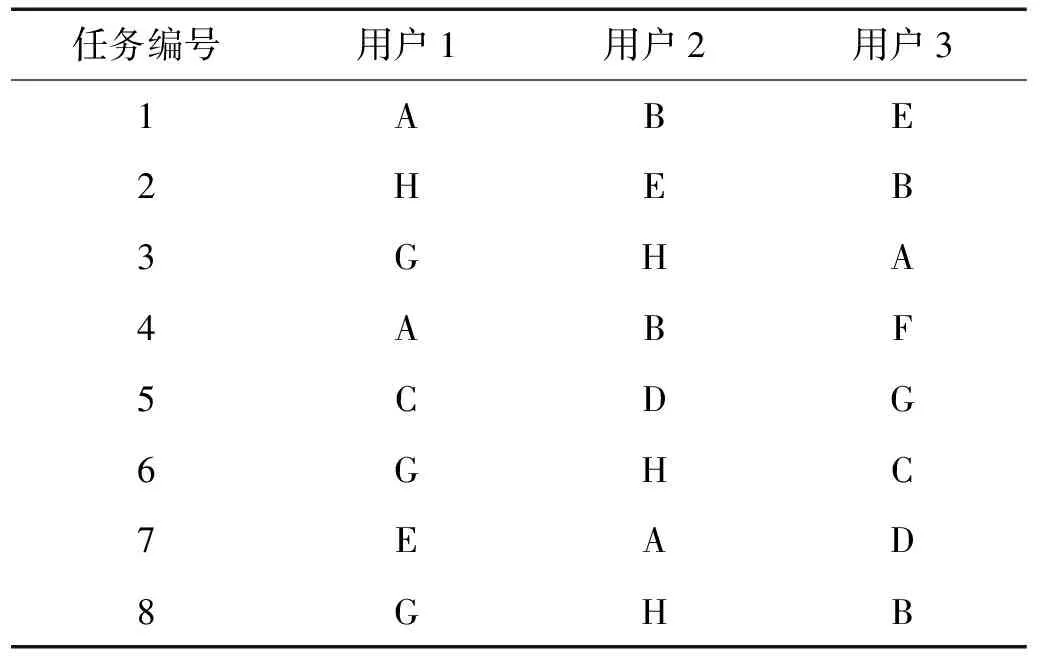
表3 各任务用户数据集设置
所提方法采用ReLU函数作为激活函数,经多次试验,本地训练迭代20次,联邦最大迭代次数50次,模型迁移本地微调次数为50次,学习率lr设置为0.001。试验使用的硬件环境:CPU型号为Intel Xeon W-2123;内存32 GB;GPU型号为NVIDIA GeForce GTX1080Ti。
本试验利用卷积层、池化层以及全连接层的堆叠,构建了基于CNN的滚动轴承故障诊断模型作为联邦学习过程中的本地模型。特征提取层由4个卷积层和4个最大池化层构成,分类器由全连接层构成,具体结构如表4所示。
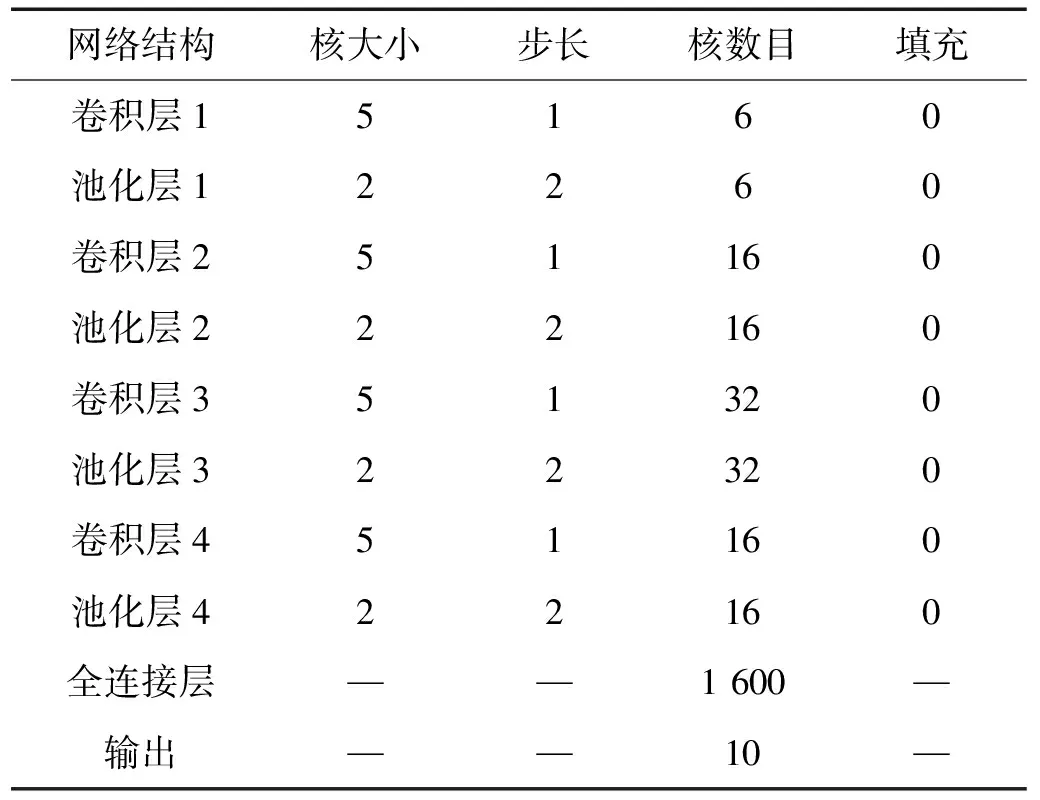
表4 卷积神经网络参数
4.2 逐层解冻策略试验
为保留合适的共享模型层数,验证不同保留层数对分类效果的影响,采取逐层解冻策略进行试验,即用户收到共享模型后,保留共享模型5层中部分层的网络参数并将其冻结,微调未冻结的网络参数。本节试验中,对8个任务分别进行保留4层、保留3层和保留2层3种情况试验。具体试验结果如表5所示。为了更清晰地表示不同保留层数对分类效果的影响,将试验结果以雷达图形式表达,如图8所示。
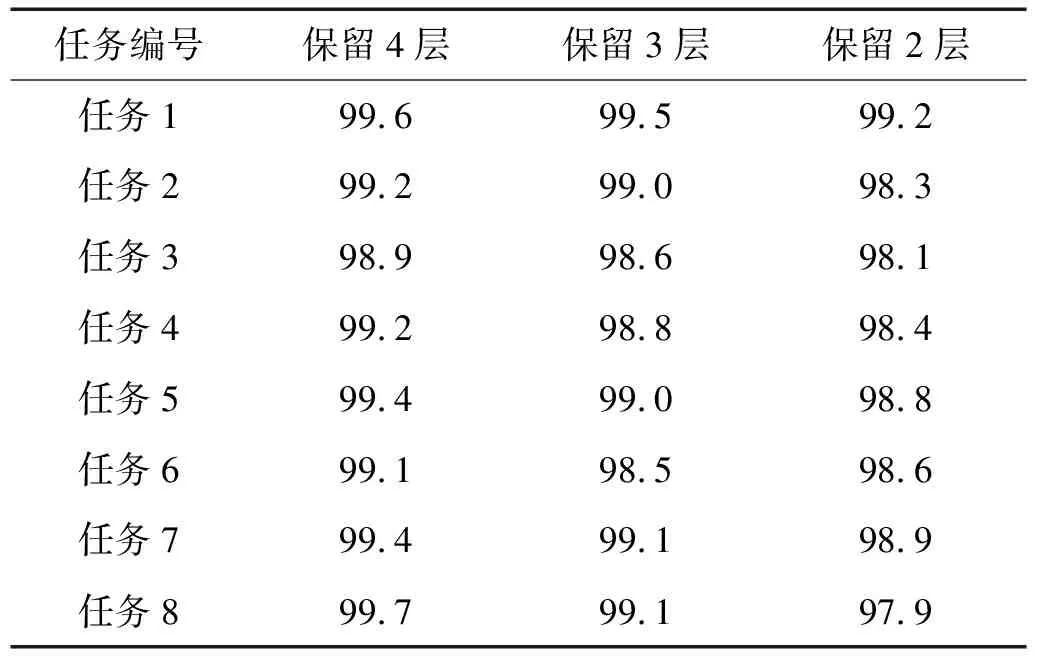
表5 不同保留层数准确率对比试验

图8 不同保留层数准确率对比雷达图Fig.8 Radar image of contrast experiment of accuracy for different retention layers
通过观察图8可得,保留前4层模型参数和保留前3层模型参数两种策略,部分任务分类效果基本持平,但仍有一部分任务在保留前3层模型参数时低于保留前4层模型参数;而保留前2层模型参数均低于以上两种策略。综上所述,本文将保留共享模型前4层参数进行后续试验。
4.3 不同参数稀疏化度对比试验
为了验证不同参数稀疏化度对分类效果的影响,选取合适的参数稀疏化度,选用60%,70%,80%,90%,100%共5种参数稀疏化度进行实验研究。
分别对任务1到任务8进行5种不同的参数稀疏化度对比试验,每个任务试验结果为3个用户测试准确率的平均值,如表6所示。
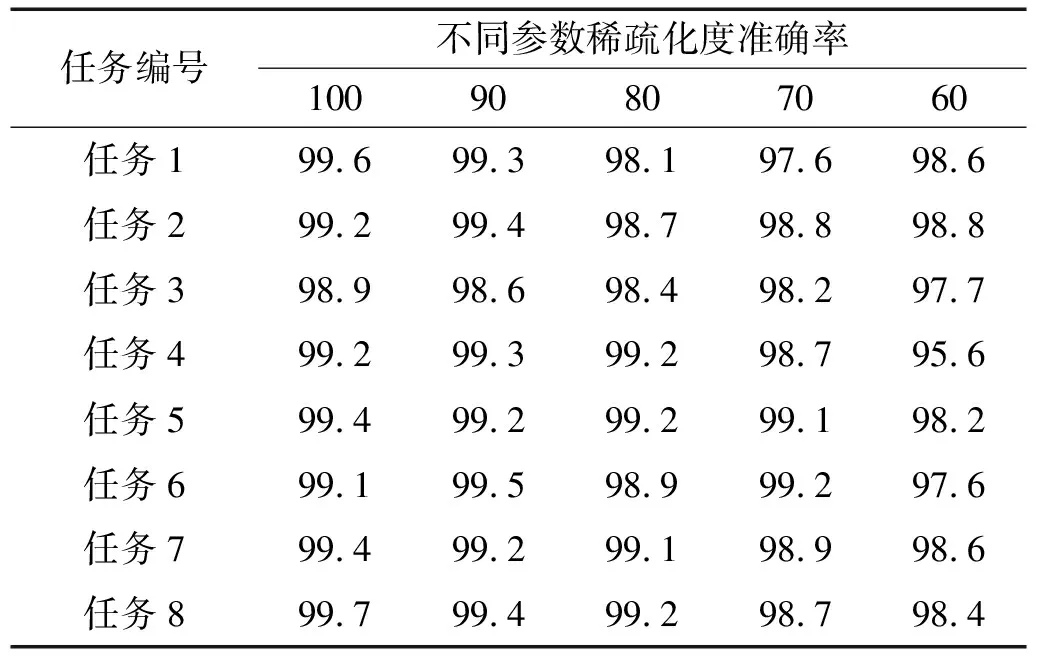
表6 不同参数稀疏化度对比试验
为了更清晰地表示不同参数稀疏化度对分类效果的影响,将试验结果以折线图形式表达,如图9所示。
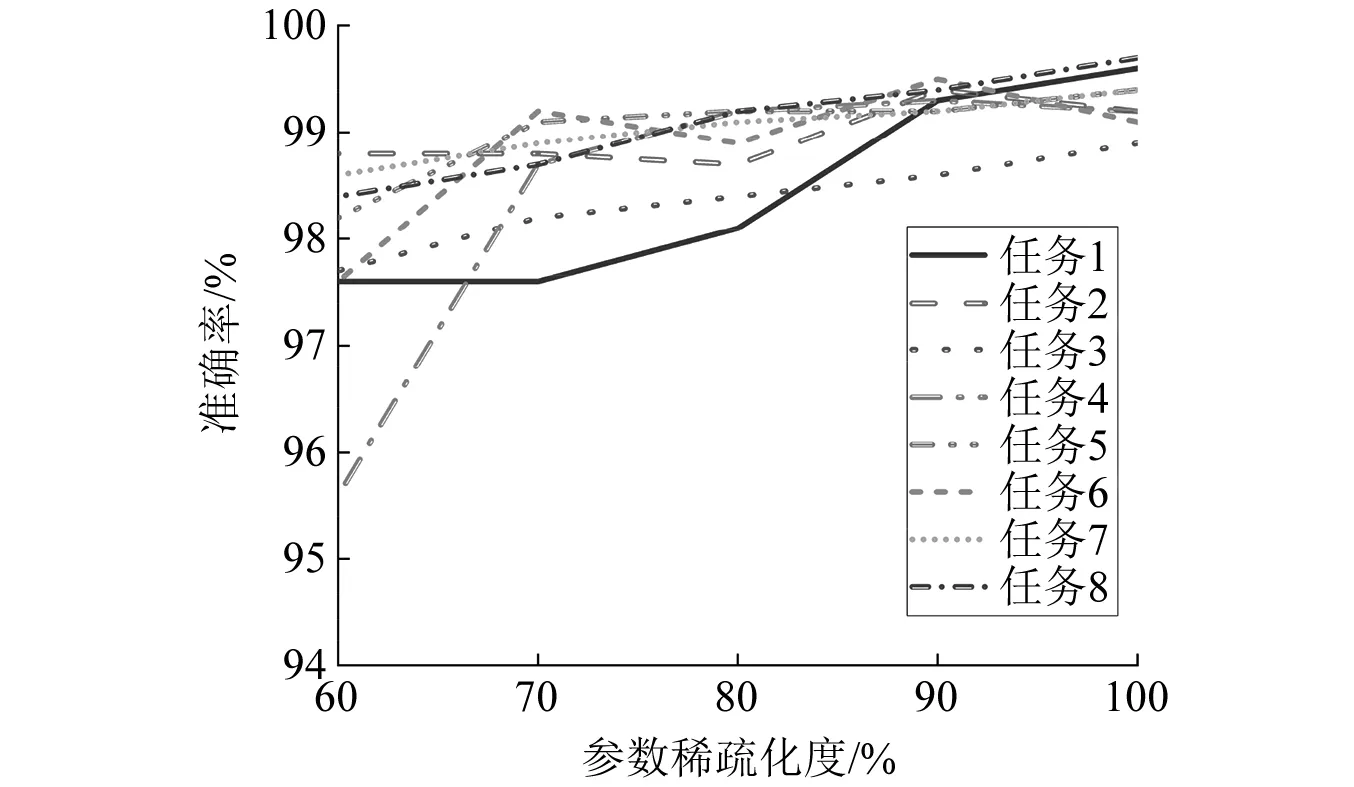
图9 不同参数稀疏化度折线图Fig.9 Line chart of different parameter thinning degrees
通过分析图9可知,参数稀疏化度为90%时,分类准确率对比100%几乎没有下降,而参数稀疏化度为80%,70%和60%时,准确率均有不同程度下降。因此,后续试验将采用90%参数稀疏化度进行后续试验。
4.4 联邦对比试验
为进一步验证所提方法的有效性和优越性,将本文所提联邦迁移学习方法与方法1和方法2进行比较。
方法1为用户使用联邦学习协同建立故障诊断模型,但不使用本地数据集微调共享模型,且方法1用户数据集设置与所提方法相同;方法2为用户仅使用本地数据建立故障诊断模型。本节试验在8组不同的任务上测试模型分类效果,试验结果为用户1、用户2和用户3测试准确率的平均值,如图10所示。

图10 所提方法与传统方法对比试验Fig.10 Contrast experiment of the proposed method and traditional methods
由图10可知,所提方法诊断准确率相比方法1可提升9.5%左右,相比方法2可提升1.2%~2.3%。
综上分析可得,方法2由于用户本地带标签样本数量过少,导致缺乏足够的有效信息建立高质量故障诊断模型;而方法1由于不同规格滚动轴承振动数据之间分布差异较大,直接采取联邦学习方法诊断效果甚至低于方法2。
4.5 扩展试验
4.5.1 本地数据集不同样本数量试验
为验证本文所提方法在其他样本数设置下的有效性,将4.4节中每个用户持有300个训练样本情况扩展为每个用户持有200个、100个和50个训练样本,其余设置均与4.4节相同。试验结果为用户1、用户2和用户3测试准确率的平均值,如图11所示。

图11 不同样本数设置试验Fig.11 Experiment results with different sample numbers
图11(a)为每个用户持有每类20个样本时的试验结果,从中可以发现所提方法准确率相比方法1平均可提升10%左右,相比方法2最高可提升2.7%~3.4%;图11(b)为每个用户持有每类10个样本时的试验结果,从中可以观察到所提方法准确率相比方法1平均可提升10%左右,相比方法2可提升2.2%~4.5%;图11(c)为每个用户持有每类5个样本时的试验结果,从中可以观察到所提方法准确率相比方法1可提升15%左右,相比方法2可提升4.1~7.1%。
综上分析可得,所提方法相比方法1和方法2,在不同样本数情况下均有不同程度的提升,尤其是在本地数据样本数较少时,分类准确率提升更为显著。
4.5.2 泛化试验
为验证本文所提方法具有较强的泛化性,使用CWRU和MFPT两种不同的轴承数据库进行验证。MFPT数据集为NICE规格轴承振动数据,有内圈故障(IR)、外圈故障(OR)和正常(N)三种状态,采样频率48.828 kHz,转速25 r/s。试验中将任务1到任务4设置的数据集分别作为源域,将另一种不同规格的NICE轴承数据集作为目标域。本试验将4.4节中前4个任务协同训练得到的共享模型作为源域预训练模型,将每类10个样本,共30个样本的NICE轴承数据集作为目标域训练数据,将1 000个样本的NICE轴承数据集作为目标域测试数据,具体任务设置如表7所示。本节试验将使用NICE数据微调共享模型作为方法1,将仅使用NICE轴承数据建立故障诊断模型作为方法2。试验结果如表8所示。

表7 泛化试验任务设置

表8 泛化试验准确率
由表8的试验结果分析可知,使用每类10个样本的NICE轴承数据独立建模,准确率仅为89.2%,而使用所提方法在4个不同任务中,均有不同程度的提升。为了更加直观地描述本文所提方法在不同规格滚动轴承故障诊断问题中的有效性,引入多分类混淆矩阵对诊断结果进行分析。受限于文章篇幅,仅以任务9的试验结果为例,绘制混淆矩阵如图12所示。
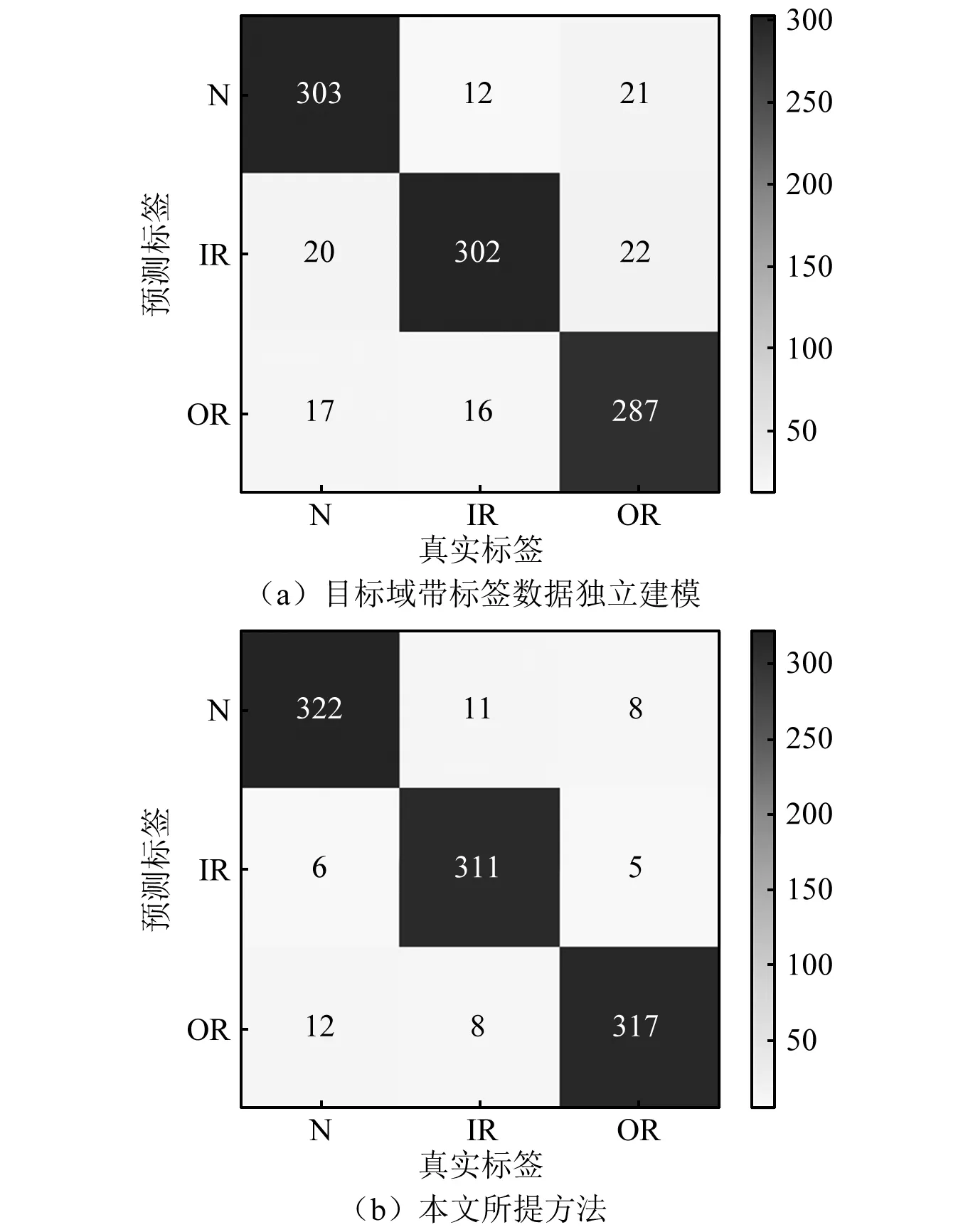
图12 滚动轴承故障诊断混淆矩阵Fig.12 The confusion matrix of rolling bearing fault diagnosis
5 结 论
针对不同规格滚动轴承振动数据分布差异大、部分已知标签数据稀缺影响诊断结果的问题,提出一种基于联邦模型迁移学习的故障诊断方法。通过多组试验验证,得到如下结论:
(1)提出逐层解冻保留策略,保留共享模型部分层的参数并利用用户本地数据微调其余层,分别保留共享模型前几层参数进行对比试验,最终确定保留共享模型前4层参数,微调最后一层模型参数分类效果最佳。
(2)提出利用差值更新和参数稀疏化算法改进联邦学习参数传递策略。通过5种不同的参数稀疏化度对比试验,选取90%作为改进参数传递策略的参数稀疏化度,能够保证不影响模型分类效果的同时,进一步提升模型参数传递过程的可靠性。
(3)提出一种新的基于联邦模型迁移的不同规格滚动轴承故障诊断框架,该框架能够在多用户轴承数据孤岛隐私分布且部分规格轴承带标签振动数据稀缺的情况下有效地建立故障诊断模型,所提方法相较用户使用本地数据独立建模,诊断准确率可提升1.2%~7.1%,且相较于用户直接进行联邦可提升至少9.5%,证明了所提方法的有效性。经NICE轴承数据集泛化试验,证明所提方法泛化性能较强。
试验中使用2个数据库的不同规格的滚动轴承振动数据进行了试验研究,但未对实际工况下的轴承振动数据进行验证,这将是后续研究的重点。
