水下爆炸冲击因子异化特征研究

姚熊亮, 王志凯, 赵 坤, 史冬岩

(1. 哈尔滨工程大学 船舶学院,哈尔滨 150001; 2. 哈尔滨工程大学 机电学院,哈尔滨 150001)

随着武器装备的发展,现代水雷等水中兵器战斗部对舰船等目标的毁伤以水下非接触爆炸冲击波作用为主,因此研究舰船结构在水下非接触爆炸作用下的冲击响应具有重要意义。虽然开展实船试验可以最准确的获取相关响应数据,但是实船爆炸试验的成本高昂,并且具有操作复杂及试验重复性差等不足,所以在实际前期研究中常采用缩比模型试验,再通过相似准则对原型冲击响应评估。

为了描述缩比模型与原型冲击响应的相似准则,学者们提出了冲击因子[1]这一相似准则。传统冲击因子定义中认为对于同一目标结构,若冲击因子相等,则其水下爆炸的冲击响应近似相等[2-3]。胡宏伟等[3]从冲击波毁伤的角度表述了冲击因子的物理意义。截至目前,大量已有试验和数值计算结果表明,利用传统冲击因子,通过缩比试验模型毁伤结果不能很好地描述原型目标结构的毁伤效果。姚熊亮等[4]从爆炸入射能量角度,考虑冲击波波振面的球面特征和爆心与结构的相对位置,提出了一种冲击因子来描述水下爆炸载荷。因对于爆距较远的水下非接触爆炸冲击波,在工程分析中一般等效为平面波,所以该冲击因子的定义中没有考虑毁伤目标的结构特性,其适用范围存在局限性。模型与原型试验存在相似率[5-7]问题,所以使用冲击因子描述水下爆炸作用下的冲击响应时,不能忽视毁伤目标的结构特性的影响。水下爆炸产生的冲击波常常被近似为平面波,目前将球面冲击波等效为平面波的假设是从冲击波在结构表面上的整体能量的损耗角度定义。Hu等[8]分析了水下爆炸产生的球面波作用下,结构表面的整体冲量,提出并验证了一种考虑球面波效应的水下爆炸冲击因子。该冲击因子可以表征不同当量的爆源,在水下非接触爆炸情况下,对平板结构产生的冲击能量。实际舰船上不仅存在平板结构,还有复杂的加筋板架等结构。该冲击因子从水下爆炸冲击波的能量方面出发,考虑了毁伤变形的相似性。李德聪等[9]从水下中远场爆炸相似率、结构响应相似率出发,结合冲击因子所表征的物理意义,对传统冲击因子修正方法进行了评述与探讨。在传统冲击因子的基础上考虑结构响应相似率,并分别提出了几种传统冲击因子的使用条件。将水下爆炸结构响应与水下爆炸相似率分开讨论,但在实际工程分析中二者是密不可分的。

本文以正面挡水,背面临空的平板、加筋板架和舱段结构为研究对象,从冲击波在结构表面的整体冲量和水下爆炸结构毁伤相似性方面入手,深入讨论了水下非接触爆炸冲击波的平面波效应,并在满足单值量相似的条件下,推导了一种新型水下非接触爆炸冲击因子。采用数值模拟与试验相结合的方法,讨论了不同缩比尺情况下,试验模型水下爆炸冲击响应问题。通过考察目标结构变形挠度、变形速度和应力等三个无量纲物理量的相似性,验证了新型冲击因子的可靠性。

1 传统水下爆炸冲击因子回顾

对于同一类物理现象,如果单值量相似,而且由单值量组成的相似准则在数值上相等,则现象相似。水下爆炸载荷与舰船冲击响应的影响因素主要涉及到药包质量、爆距、爆炸方位以及结构特性等(如图 1所示)。传统冲击因子主要有两种形式:一种是基于冲击波超压峰值的冲击因子,一种是基于结构遮挡冲击波能量相等的冲击因子。两种冲击因子从自由场水下爆炸冲击波载荷特征的角度描述水下爆炸相似性规律,忽略了单值条件中的几何条件即目标结构特性这一重要因素。

1.1 自由场水下爆炸冲击波载荷相似理论

水下爆炸现象与一般水动力学现象不同,其作用力具有冲击性的特点,水动力学中的一些相似常数(如雷诺数(Re)等)不必考虑,同时一次冲击波不用考虑流体特性(如重力)。

设炸药单位质量包含的化学能为ρe,化学能对冲击波能的转化率为ηe,则在爆炸过程中产生的冲击波能量E(单位:J)为

E=Wρeηe

(1)

当爆距R(单位:m)远大于舰船结构尺度l(单位:m)时,可以认为冲击波是以平面波的形式作用在舰船结构上,则舰船结构遮挡的冲击波能量为

(2)

式中:ES为舰船结构遮挡的冲击波能量,J;Se为舰船结构遮挡冲击波能量的面积,m2。

水下爆炸冲击波指数衰减经验公式为

(3)

式中:Pm为冲击波超压峰值,Pa;τ为冲击波脉宽,s; Δt为冲击波波阵面到达时刻后时长,s。其中各参数的计算公式为

(4)

(5)

(6)

(7)

式中:I为单位面积冲击波的冲量,Pa·s;E′为单位面积冲击波的能量,J;Ki(i=1,2,3,4)和ai(i=1,2,3,4)为与炸药(TNT)相关的材料常数。

选取可以表征水下爆炸这一现象的主要物理量,各物理量使用质量(M)、长度(L)和时间(T)三个基本量纲表征的幂次表达式分别为:药量W(M)、爆距R(L)、冲击波的脉宽τ(T)、水中声速C(LT-1)、物面压力Pm(ML-1T-2)、爆炸冲击波能量E(ML-2T-2),则量纲矩阵如式(8)所示

(8)

由上述量纲分析可以得到自由场水下爆炸的无量纲π项

(9)

对相关π项进行代数转换

(10)

将式(2)代入π′3中,可得

(11)

1.2 基于冲击波超压峰值相等的冲击因子讨论

基于冲击波超压峰值相等定义的冲击因子C1为

(12)

式(10)中, π′2即为冲击因子C1,基于冲击波超压峰值相等的冲击因子C1定义为对于同一结构,当两种工况的冲击因子C1相等时,则在舰船结构的入射点处的超压峰值Pm相等,将超压峰值作为表征水下装药爆炸威力的一个表征量。冲击因子C1定义中认为当入射点处的超压峰值Pm相等,则结构的冲击响应近似相等,这是基于几何相似时模型与原型必须承受相同大小的压强的要求。

冲击因子C1充分利用了目标结构满足几何相似时原型与模型压力相等,但未能说明模型与原型冲击波的入射能量相等。物面表面压力和入射波、反射波、透射波有关,特别是透射到结构内时的透射波,当它再次反射到物面时,会影响到入射冲击波波尾。反射回物面的波与结构特征有着密切关系,如果忽略目标结构特征这一几何条件,这不满足单值条件,同样只解决了水下爆炸相似问题中的一部分,只有结构特征严格满足相似,这样才能解决问题。

1.3 基于能量相等的冲击因子讨论

基于结构遮挡能量相等的冲击因子C2认为当冲击波以平面波的状态作用到同一舰船结构上,结构遮挡冲击波能量的面积Se不变和舰船结构遮挡的冲击波能量ES不变时,依据式(11)可得常用的基于平面波效应的冲击因子

(13)

1.4 传统冲击因子局限性分析

两种传统冲击因子从不同的角度出发定义了冲击因子的形式,在表征水下装药非接触爆炸威力方面二者并无本质的区别,且相互之间存在确定的转换关系,同时二者在使用时均存在一定的限制条件,下面将分别对两种传统冲击因子的使用局限性进行讨论:

式(12)表示的冲击因子C1在使用中,存在以下情况,当缩比模型与原型的几何比例(缩尺比)过小时,水下爆炸形式可能从远场爆炸转变为近场爆炸,由式(7)可知,此时结构单位面积上承受的冲击波能量发生改变,导致缩比模型与原型的毁伤效果不同。针对这一问题,姚熊亮等和李德聪等从水下爆炸相似规律方面对冲击因子C1提出补偿条件。提出的补偿条件主要针对冲击波的传播状态和涉及的冲击环境参数,没有考虑到单值物理量相似条件,所以在使用时需要针对不同情况合理设计试验方案。

式(13)表示的冲击因子C2在定义中不仅没有对平面波效应给出明确判据,而且存在当模型按缩尺比进行缩比时,药包与结构的相对位置发生变化,导致结构在垂直于冲击波方向上的投影面积Se发生变化,由式(11)可知,此时不满足冲击因子C2的使用条件。针对上述问题,姚熊亮等、Wei等、Hu等从平面波定义以及冲击波的球面波效应等方面对冲击因子C2提出了修正。提出的修正条件主要依据爆距与药包半径的比值大小来定义平面波,没有考虑到冲击波传播过程中的冲量衰减,也未计及单值物理量相似条件,所以冲击因子C2在使用中需要注意使用条件,其使用范围存在局限性。

针对两种传统冲击因子的不足,学者们虽然提出了部分修正条件,但还有待进一步完善。在研究水下非接触爆炸结构毁伤相似规律时,不仅需要考虑爆炸冲击波的传播状态和水下爆炸相似规律,同时需要考虑单值条件问题。因此本文在满足单值物理量相似的要求下推导了一种新型水下爆炸冲击因子。

2 考虑水下爆炸相似性异化特征的冲击因子讨论

根据1.4节对传统冲击因子的局限性分析可知,在研究水下爆炸结构毁伤相似规律时,不仅需要考虑水下爆炸的爆源相似规律同时需要考虑单值物理量相似。水下爆炸过程中产生的爆炸冲击波是以球面波形式向外传播,通常处理这一问题的方法是将球面冲击波假设为平面波。针对上述问题,本文从以下两方面进行讨论:首先,为解决球面波如何近似为平面波的问题,本文从冲击波传播状态的角度对爆炸冲击波的平面波效应进行了讨论;然后,结合舰船在水下爆炸条件下的几何条件、介质条件、边界条件和初始条件等因素,对考虑目标结构特性的水下爆炸结构毁伤相似规律进行了系统化分析。

2.1 水下非接触爆炸冲击波的平面波效应讨论

依据爆炸冲击波在水中的传播规律构建平板结构与爆炸冲击波的物理模型。设存在任意空间坐标系,坐标原点在边长为d厚度为δ的正方形平板的中心位置,冲击波与平板产生冲击响应的平面为xoy平面。装药爆心设定在z轴上的A点,爆心(A点)与坐标系原点O(平板中心点)的距离为爆距R,爆心与平板边缘点的距离为L,爆心与平板x轴方向的两侧边缘点形成的夹角为等效平面波限制角β,具体情况如图2所示。

根据几何简图(如图2所示)从数学几何角度分析,爆距R和平板结构边长d可以表示为

(14)

(15)

设当式(15)中β/2在趋近于0的某一邻域内时,将正弦函数sinβ/2进行泰勒级数展开,式中k为自然数

(16)

若sinβ/2=β/2,此时最大误差值为(β/2)3/3!,当β/2=0.1 rad时误差为0.000 17,误差在工程分析可接受范围内,因此存在0≤β/2<0.1 rad时sinβ/2≈β/2,此时cosβ/2≈1。当等效平面波限制角β满足上述要求时,即0≤β/2<0.1 rad,根据式(14)可得R/L=0.999 99。可以认为当β/2满足上述约束条件时,可以认为爆距R等于爆心与平板边缘点的距离L。结合水下爆炸产生的冲击波以速度C向四周传播,由图2可得爆心处产生的冲击波到达平板结构中心点和边缘点的时间间隔为

(17)

式中:τ为冲击波的脉宽;C为冲击波的传播速度。

通过以上数学分析,可认为当R,L和C当满足式(17)时,认为爆炸冲击波同时到达平板结构的中心点和边缘点,此时,水下爆炸冲击波可视作平面波作用在平板表面。

为了更充分的论证式(17)所描述条件的合理性,接下来从水下爆炸作用在平板结构上整体冲量的角度进行深入的讨论。设爆心处产生的冲击波到达平板结构中心点和边缘点的时间间隔控制在一定的范围内,则这一控制范围为

(18)

式中:τ为冲击波的脉宽,s;C为冲击波的传播速度,m/s;α为冲击波达到结构中心点与结构边缘点的相对时间差值系数。

如图2所示,在球面冲击波传播的方向上取一块正方形平板,平板边长为d,厚度为δ。当装药布置在结构中心点(坐标系原点O)的z轴方向A点时,作用在整个平板上的整体冲量IG为

(19)

式中,P(x,y,t)为球面冲击波作用下正方形平板上任意一点的冲击波压力,由式(2)和式(3)可知

(20)

式中:W为装药(TNT)质量;τ为冲击波的脉宽;x和y为平板上点在空间坐标系的坐标;R为爆距;K1和a1为与装药(TNT)相关的材料常数。

当将球面冲击波近似等效为平面波时,作用在上述整个平板上的整体冲量IP为

(21)

式中,P(R,t)为平面冲击波作用下正方形平板上任一点的冲击波压力,由式(2)和式(3)可知

(22)

式中:W为装药(TNT)质量;τ为冲击波的脉宽;R为爆距;K1和a1为与装药(TNT)相关的材料常数。

定义作用在上述平板上的冲击波整体冲量的相对误差ε为

(23)

从式(15)和式(16)可知α值的变化对球面冲击波的平面波效应存在影响。通过作用在平板上的整体冲量相对误差ε的大小,可以有效地反映出球面冲击波与平面冲击波的差异性。α值对作用在平板上的整体冲量相对误差ε影响较大,因此,有必要对α值进行讨论分析来验证式(17)。现依据实际水雷装药设计原型试验载荷,取载荷输入参量为装药(TNT)当量为500 kg,爆距为30 m,平板尺寸为6 m×6 m,计算作用在平板上的整体冲量相对误差。计算结果统计如表1所示,表中:α为冲击波达到结构中心点与结构边缘点的相对时间差值系数;R/L为爆距R与爆心与平板边缘点的距离L的比值;β为等效平面波限制角;ε为平板整体板上冲量的相对误差。

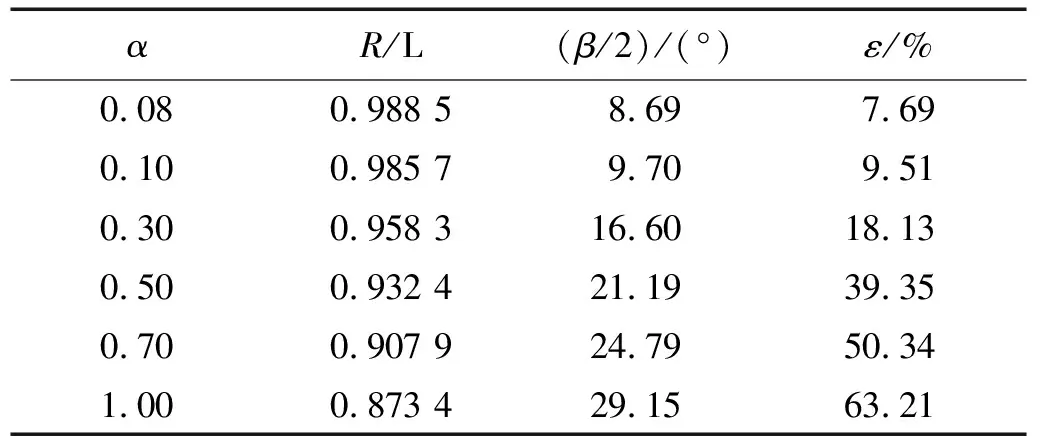
表1 α值对于冲击波的平面波效应的影响

从表1结果可知,α值对作用在平板整体板上冲量的相对误差ε影响较大,且相对误差ε随着α值的增大而增大。图3为α值对相对误差值ε的影响曲线示意图。从图3中可以看出,当α值取值在0.08～0.1时,相对误差ε差值在3%以内,即当α≤0.1时,平板上整体冲击波冲量相对误差ε和等效平面波限制角β的变化较小。α=0.1时,不仅满足式(15)的数学几何条件,同时满足平板上整体冲击波冲量相对误差ε在10%以内,此时球面波冲击波可以近似认为是平面波。而Wei等提出的基于冲击能量损耗提出的球面冲击波近似认为是平面波的约束条件为式(22)

(24)

Wei等认为当α=1时,爆炸冲击波的能量损耗在可接受范围内,冲击波可以近似为平面波。而当α=1时,通过计算平板上的整体冲量相对误差ε为63.21%,此时球面和平面冲击波在平板上整体冲量差异性较大,导致计算结果会存在较大的误差。本文提出的α取0.1(如式(15))时,爆炸冲击波的能量损耗不仅满足Wei等提出的约束要求,同时从板上整体冲量的角度出发,作用平板上整体冲击波冲量相对误差ε在10%以内,满足工程分析中普遍容许的误差范围。因此,本文认为当满足式(15)条件时,即α取0.1,水下爆炸球面冲击波可以近似视为平面波作用。

2.2 计及目标结构特征的新型水下爆炸冲击因子

在舰船结构遭受水下爆炸冲击波冲击这一过程中,为了保证模型与原型之间各类主要单值物理量满足几何条件、介质条件、边界条件以及初始条件,从而使模型与原型的物理量之间达到单值条件。本文选取可以表征这一现象的主要物理量,及其使用质量(M)、长度(L)和时间(T)三个基本量的量纲幂次表达式[10]分别为:药量W(M)、爆距R(L)、爆源水深h(L)、冲击波到达船体表面的吃水D(L)、冲击波的脉宽τ(T)、水中声速C(LT-1)、水中阻抗ζw(ML-2T-1)、空气阻抗ζα(ML-2T-1)、船体结构材料阻抗ζs(ML-2T-1)、物面压力Pm(ML-1T-2)、刚体运动速度U(LT-1) 、爆炸冲击波能量E(ML-2T-2)。量纲矩阵如式(25)所示

(25)

由上述量纲分析可以得到自由场水下爆炸的无量纲π项

(26)

将水中阻抗ζw=ρwC(C为水中的声速,ρw为水的密度),空气阻抗ζα=ραCα(Cα为空气中的声速,ρα为空气的密度), 船体结构材料阻抗ζs=ρsCs(Cs为钢中的声速,ρs为钢的密度)带入式(24),经代数运算后得到新的π项

(27)

假设模型与原型的试验均是钢制结构在水、空气的环境中进行,由于水中的声速有Cp=Cm(下标p表征原型物理量,下标m表征模型物理量),空气中的声速有Cαp=Cαm,钢中的声速有Csp=Csm,水的密度有ρwp=ρwm,空气的密度有ραp=ραm,钢的密度有ρsp=ρsm,则有:

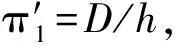
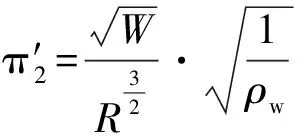
(6)文中选取的关于舰船结构的冲击波到达船体表面的吃水D(L)和船体结构材料阻抗ζs(ML-2T-1),当目标结构为平板、加筋板架和舱段结构时,同样对应目标结构的几何物理量和材料属性参数,本文选取单值物理量适用钢制结构在水、空气的环境中进行水下爆炸试验。

综上所述,当水下爆炸模型试验各主要单值物理量满足相似条件时,冲击因子可用C3表征

(28)

3 缩比试验模型设计及新型冲击因子有效性分析

本文选用某万吨级舰船的部分典型平板结构、板架结构以及舰船第143～第237肋位的舱段结构,基于平面波效应(如式(17))建立数值试验模型[11],分析依据各冲击因子设计的缩比模型试验与原型试验的毁伤相似性。在不同缩尺比情况下,从结构最大位移、变形挠度和变形速度三个物理量验证缩比模型与原型结构冲击响应的一致性。

3.1 计及目标结构特征的新型水下爆炸冲击因子

模型试验材料为945钢,密度为ρ=7 850 kg/m3,弹性模量E=205 GPa,泊松比为0.3。根据实际水雷装药设计原型试验载荷,表2给出了原型载荷数据和分别依据式(12)、式(13)和式(28)表示的冲击因子C1,C2和C3计算得到的冲击因子值,表中:Wp为原型装药(TNT)质量,Rp为原型爆距。

表2 某型舰船部分典型结构原型试验载荷及冲击因子数据

舰船结构在进行几何缩比时,需按照缩尺比λ进行缩比

Lm=Lpλ,δm=δpλ,rm=rpλ,
Dm=Dpλ,Rm=Rpλ

(29)

式中:Lm为缩比模型结构边长;Lp为原型结构边长;δm为缩比模型结构板厚;δp为原型结构板厚,rm为缩比模型药包半径;rp为原型药包半径,Rm为缩比模型爆距;Rp为原型爆距;Dm为缩比模型型材尺寸;Dp为原型型材尺寸。模型装药(TNT)质量Wm的设计是结合模型爆距Rm再分别依据式(12)、式(13)和式(28)计算得到。

(1) 平板原型试验设计:平板结构边长为6 m×6 m,光板厚度δm为0.024 m,平板的边界条件为四周简支,平板原型示意图如图4所示,具体缩比后的模型工况数据如表3所示。

表3 板架结构缩比模型试验工况表Tab.3 Plate frame scale model test condition table

(2) 板架原型试验设计:板架结构边长为6 m×6 m,光板厚度为0.024 m,横纵加强筋为T型材(尺寸为Dm1/Dm2: 0.014 m×0.16 m/0.01 m×0.36 m,其中Dm1为T型材面板尺寸,Dm2为T型材腹板尺寸。)均匀布置在结构上,板架的边界条件为四周简支。板架模型的工况设计同平板模型的相同,其中板架尺寸及T型材参数均按照式(29)进行几何尺寸缩比,具体缩比后的模型工况数据如表3所示,板架原型示意图如图5所示。

(3) 舱段模型试验设计:本文选取某型舰船第143～第237肋位的舱段结构,长为47 m,型宽为22.5 m,高为15.8 m,其中舱壁的间距分别为17 m和13 m,舱段模型其余尺寸如图6所示,舱段模型边界条件为将两侧舱壁简支。舱段模型的工况载荷设计同平板/板架模型的工况载荷设计相同,故舱段模型试验的工况载荷数据见表3。

实际船体甲板厚度沿船宽方向有所变化,图6中标注尺寸为船中纵处各甲板厚度。具体缩比后的模型工况数据如表4所示,表中δm1为一甲板厚度,δm2为实肋板厚度,δm3为双层底内底板厚度,δm4为双层底外底板厚度,舱段结构其余甲板、横舱壁和型材尺寸均按照式(29)进行设计。

由表3和表4可知,当目标结构满足几何相似缩放要求时,依据冲击因子C1(式(12))和C3(式(28))设计的模型试验工况冲击波载荷相同,此时二者工况相同。因此,本文将主要分析依据冲击因子C2(式(13))和C3(式(28))设计的模型试验工况数据。

3.2 模型与原型的冲击波载荷特征差异性分析

为了研究原型试验与依据各冲击因子设计的缩比模型试验的载荷特征差异性。本文从冲击波超压峰值、脉宽和冲量的角度,分别分析了原型和三种冲击因子条件下冲击波的差异性规律。将表3和表4中输入载荷参数依据式(4)计算得到的原型工况和不同缩比尺寸下三种冲击因子设计的工况计算结果如图7和图8所示。

图7给出了,在不同缩尺比λ情况下,依据冲击因子C1(式(1))和C3(式(28))设计的模型试验载荷峰值与原型试验载荷峰值相同,载荷脉宽减小且变化明显。依据式(5)对载荷数据脉宽进行计算后发现,模型试验的载荷脉宽与原型试验载荷脉宽的比值为缩尺比λ。分别根据式(6)计算目标结构单位面积上的冲量和式(19)计算目标结构整体冲量,发现模型试验在目标结构整体冲量和单位面积上的冲量均与原型试验计算得到的数值满足相似条件要求,比值为缩尺比λ。

图8给出了,在不同缩尺比λ情况下,随着缩比尺λ数值的减小时,依据冲击因子C2(式(13))设计的模型试验载荷峰值较原型试验载荷峰值显著增大。依据式(5)计算后得到模型试验冲击波脉宽较原型试验冲击波脉宽减小,但模型试验载荷脉宽与原型试验载荷脉宽的比值不等于缩尺比λ。依据式(19)计算目标结构整体冲量后发现依据冲击因子C2设计的模型试验在目标结构上的整体冲量与原型试验相等。

综上,在本文的计算工况中依据冲击因子C1设计的模型试验载荷特征与原型载荷满足相似条件,依据冲击因子C2设计的模型试验载荷在冲击波超压峰值和单位面积上的冲量与原型载荷同样存在较大差异。

3.3 平板-板架-舱段数值验证结果分析

评估缩比模型与原型试验的毁伤结果,往往考核的物理量有结构的位移变形量、速度响应和应力等。本文中提取结构中心点的变形挠度u、变形速度v和应力s,并对其进行无量纲化处理

y=u/L,V=v/vm,S=s/sm

(30)

式中:y为无量纲变形挠度;u为中心点变形挠度;L为结构边长;V为无量纲变形速度;v为结构中心点速度;vm为试验速度数据峰值时刻数值;S为无量纲变形速度;s为结构中心点应力;sm为试验应力数据峰值时刻数值。无量纲时间T为

T=t/tm

(31)

式中:t为历程时间;tm为试验数据峰值时刻时间值。

3.3.1 平板模型数值试验结果分析

(1) 当λ=1/2时,平板模型数值试验结果分析

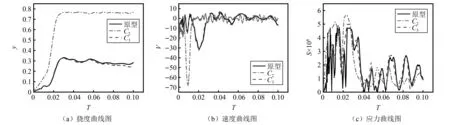
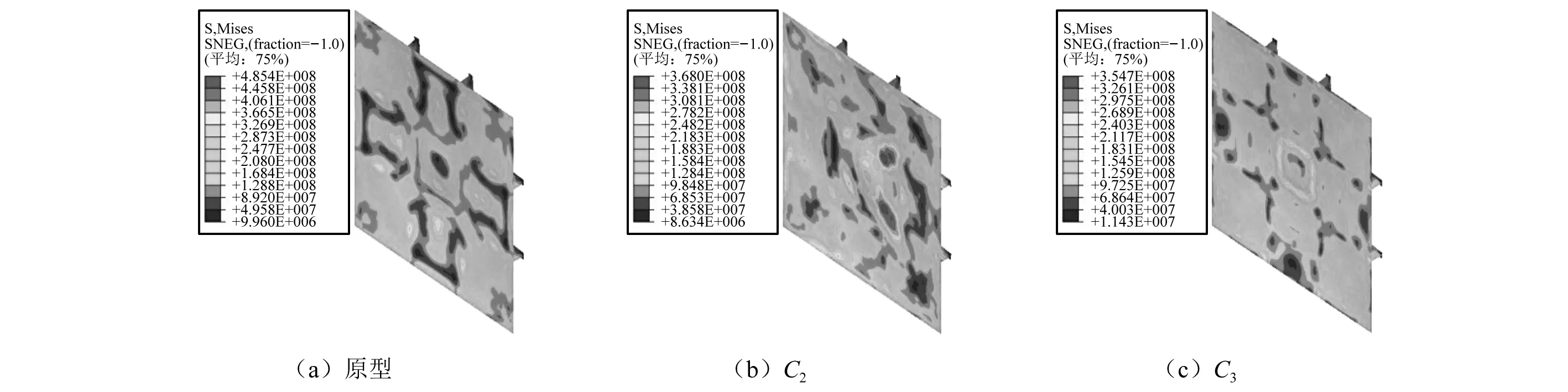
当缩尺比λ=1/2时,分别依据式(10)和式(28)计算冲击因子C2和C3,并根据计算的结果设计工况2和工况3,图9为模型与原型试验在同一时刻的应力云图。由图9可知由C2设计的模型工况作用在其结构表面的载荷特性较原型输入载荷特性发生变化,且模型试验结构上的应力与原型试验的应力状态不同。图10为结构的无量纲挠度、速度和应力变化曲线。从图10(a)无量纲挠度曲线可知,三种冲击因子对应模型试验的变形挠度曲线趋势与原型试验的大致相同,但曲线峰值和平稳后的数值不同,由冲击因子C3设计的模型试验的塑性变形挠度与原型试验误差最小,约为3%;从图10(b)无量纲速度曲线和图10(c)无量纲应力曲线可知,冲击因子C2设计的模型试验速度和应力曲线变化趋势与原型试验一致性较差,而C3设计的模型试验速度和应力变化趋势与原型试验保持一致,误差较小。

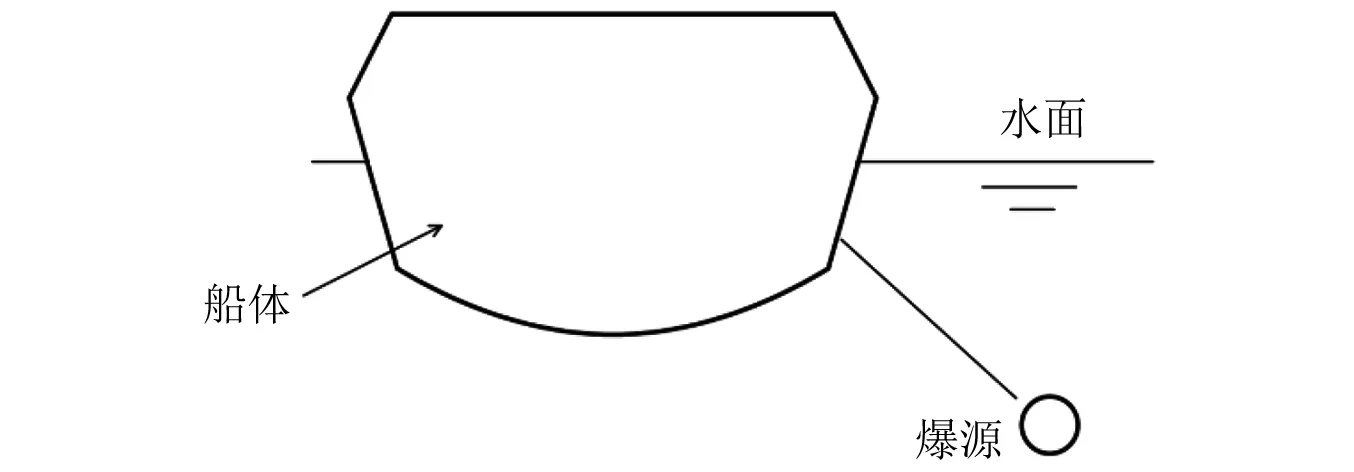
图1 爆源与船体相对位置示意图Fig.1 Schematic diagram of the relative position of the explosion source and the hull

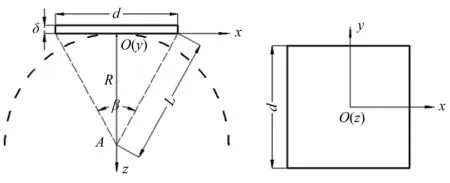
图2 平面波效应推导几何简图Fig.2 Plane wave effect derivation geometry diagram

图3 α值对相对误差值ε的影响Fig.3 The influence of the value of α on the relative error value ε

图4 平板原型结构图(mm)Fig.4 Schematic diagram of flat model (mm)

图5 板架原型结构图(mm)Fig.5 Schematic diagram of plate frame model (mm)

图6 某型舰船舱段(横剖/纵剖)模型结构图(m)Fig.6 Model structure diagram of a certain type of ship cabin (Side view/half section) (m)

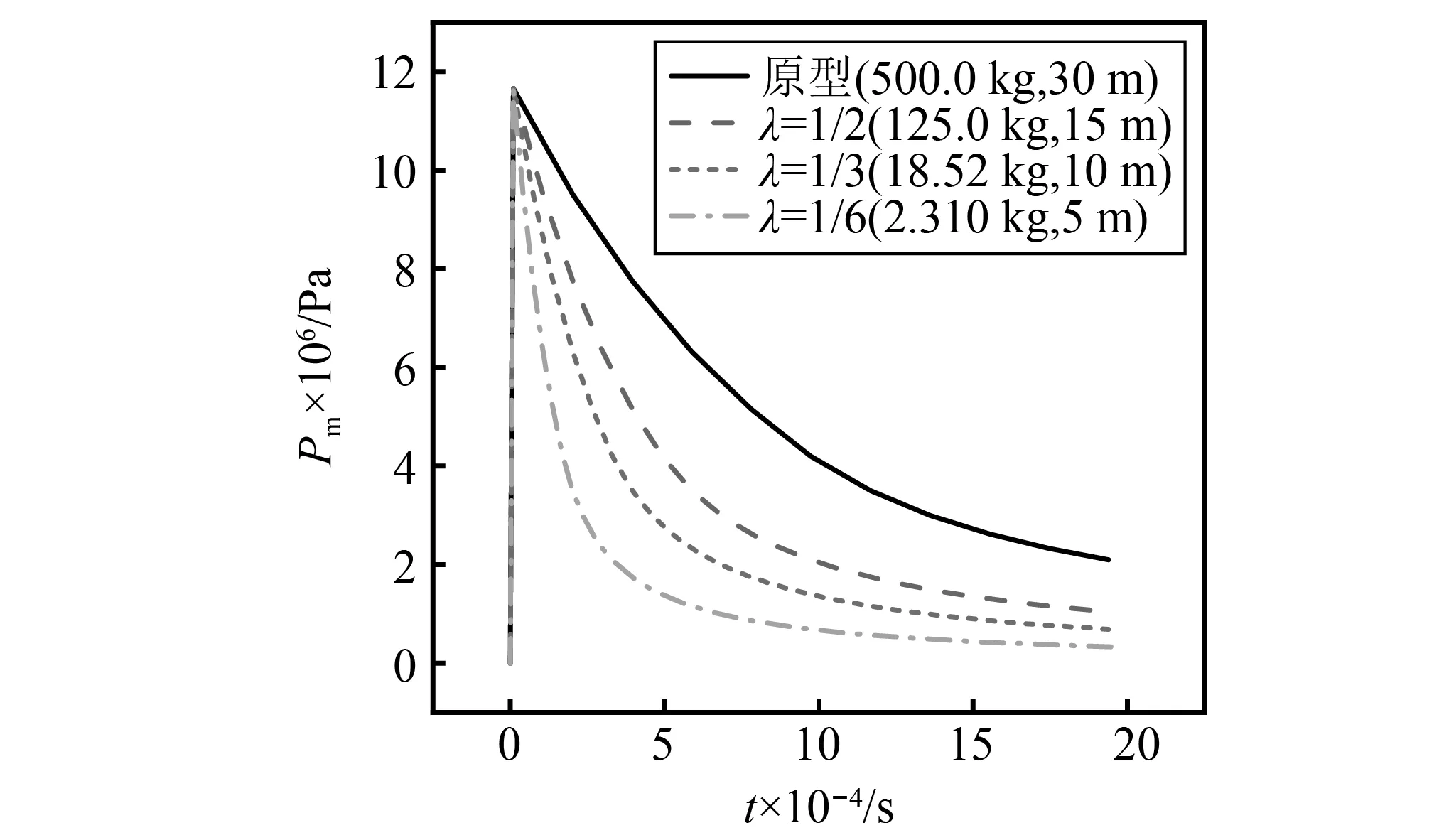
图7 原型载荷与C1(或C3)对应工况载荷对比图Fig.7 Load comparison diagram of prototype load and C1 (or C3) corresponding working conditions

图8 原型载荷与C2对应工况载荷对比图Fig.8 Comparison chart of prototype load and C2 corresponding working condition load

图9 当λ=1/2时,平板结构应力云图Fig.9 When λ=1/2, the stress cloud diagram of the flat structure

图10 当λ=1/2时,平板结构中心点的挠度、速度和应力曲线Fig.10 When λ=1/2, the deflection, velocity and stress curve of the center point of the flat structure

第3.3.1节通过对比原型试验与缩比模型试验的应力云图、无量纲挠度曲线、无量纲速度曲线和无量纲应力曲线,从数据图形的角度描述了原型试验毁伤效果与缩比模型试验毁伤效果的差异性,得到了在相同缩尺比情况下依据冲击因子C3设计的试验工况毁伤效果与原型工况毁伤效果一致性精度高,验证了冲击因子C3的可靠性。

数据图形可以直观地反映缩比模型和原型之间的相似程度,但对于缩比模型试验数据与原型试验数据的内在相关性和规律性揭示不足,因此,下面采用数学统计的方法对原型试验与缩比模型试验的无量纲挠度、速度和应力曲线数据进行相关系数分析。首先给出区间数和Spearman秩相关系数的概念,在此基础上给出区间数的Spearman秩相关系数的表示形式,然后通过计算不同模型试验与原型试验数据Spearman秩相关系数的大小得到冲击因子的优序排列[12]。

(32)

式中,若aL=aU时,则该区间退化为实数。

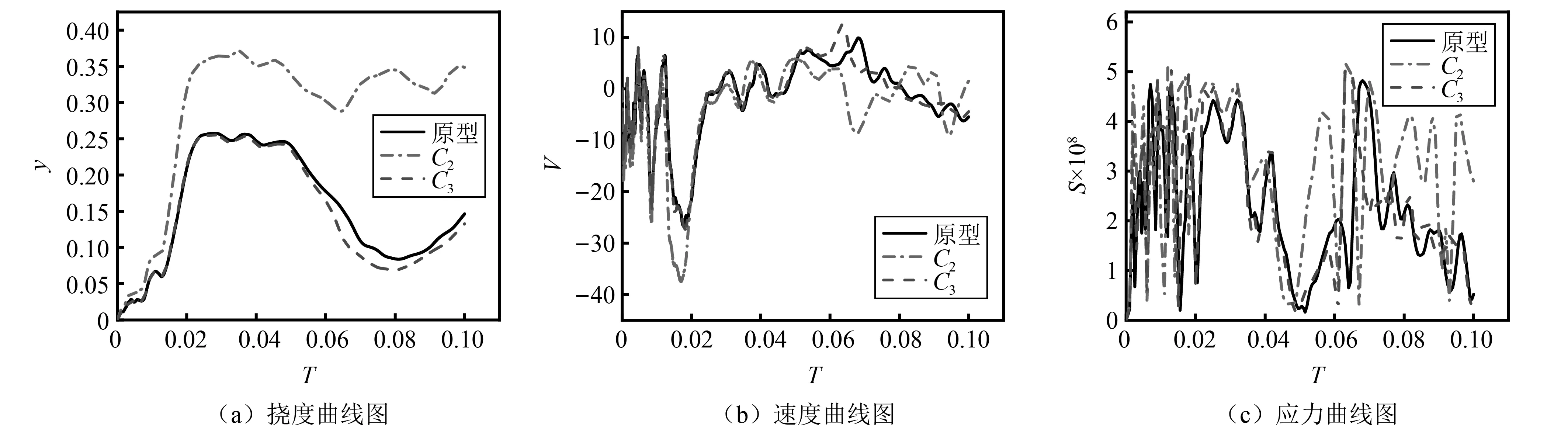
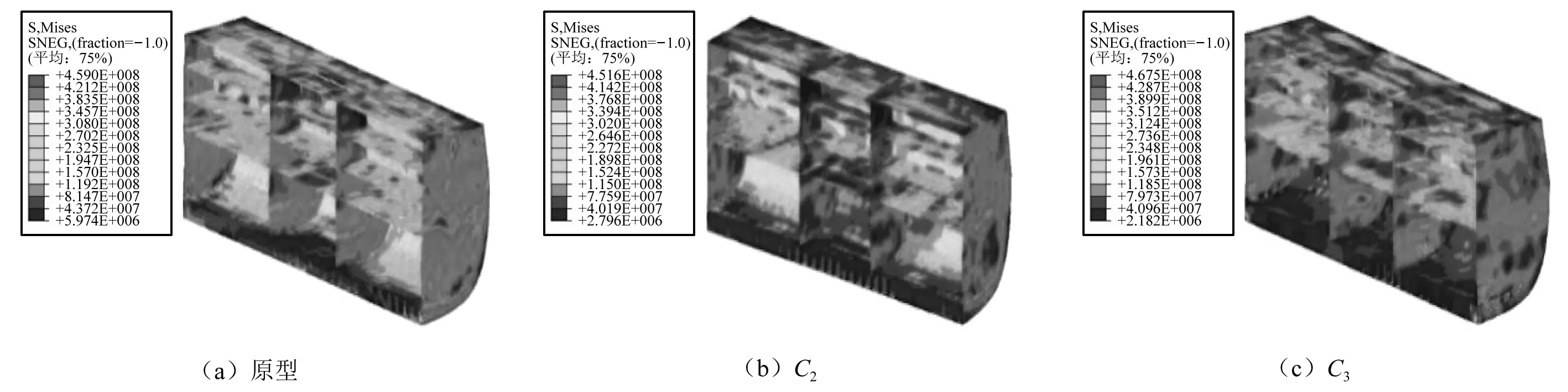
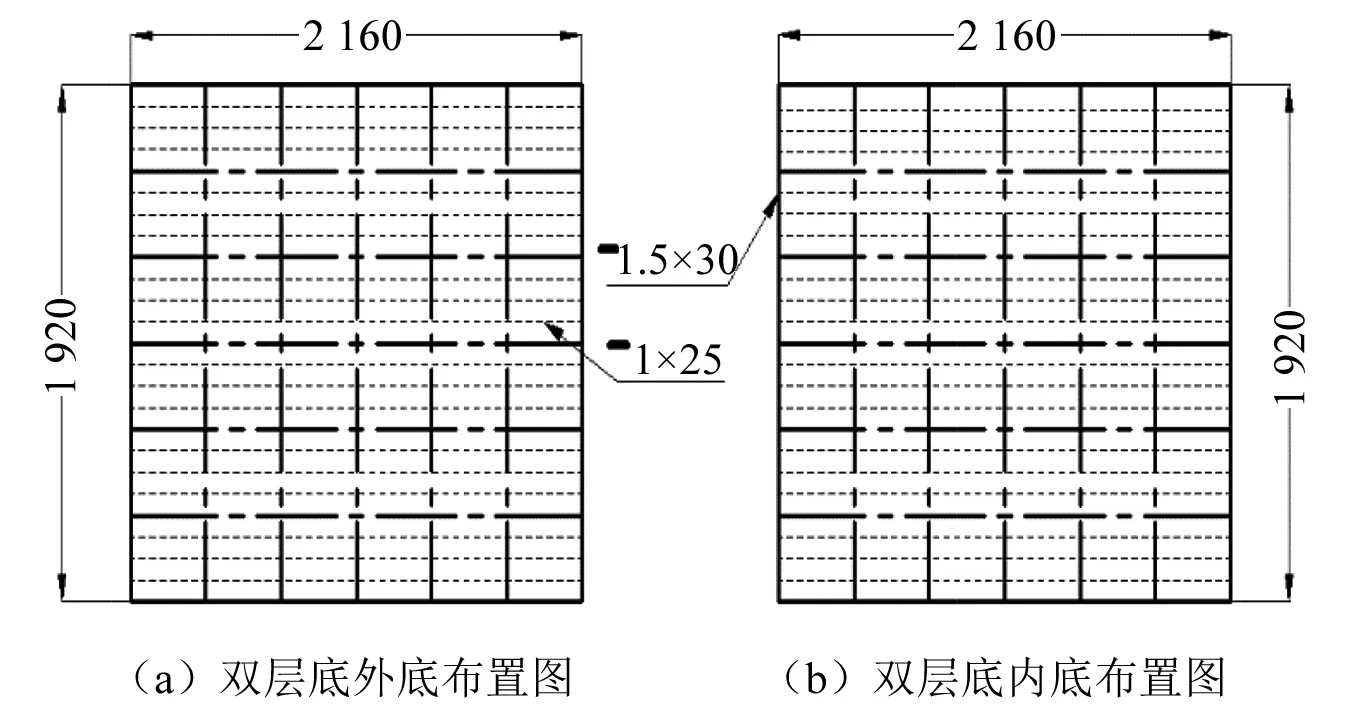
设(x1,x2,…,xn)为来自总体X的样本,将xi(i=1,2,…,n)从小到大进行排列得到x(1)

设(x1,y1),…,(xn,yn)是来自变量X和Y的随机样本,将x1,x2,…,xn和y1,y2,…,yn按从小到大排序,则Spearman秩相关系数为

(33)

式中,di=R(xi)-R(yi),i=1,2,…,n,R(xi)和R(yi)分别为xi和yi的秩。

式(33)中并不要求变量X和变量Y中任意两个值的秩相同,只要满足任意值的秩小于观测值的个数n即可。显然,Spearman秩相关系数具有以下性质:r(A,B)=r(B,A);如果A=B,则r(A,B)=1;r(A,B)的绝对值小于等于1。

根据式(33)得到相应的相关系数,其与变量之间的相关性强弱关系如表5所示。

表5 相关性与相关性系数Tab.5 Correlation and correlation coefficient

表5给出了当相关系数0

表6 当λ=1/2时,平板模型试验与原型数据的秩相关系数

如表6所示,当缩尺比λ=1/2时,依据C3设计的缩比模型试验在无量纲挠度、无量纲速度和无量纲应力曲线的相关系数最大,表明依据冲击因子C3设计的缩比模型试验可以很好的评估原型试验的毁伤效果,从统计学的角度进一步验证了冲击因子C3的可靠性。对于平板模型,当缩尺比λ=1/2时,依据冲击因子C3设计的模型试验能很好地转换到原型试验。

(2) 当λ=1/3时,平板模型数值试验结果分析

当缩尺比λ=1/3时,分别依据冲击因子C2和C3设计的工况5和工况6在同时刻的应力云图如图11所示。图12为结构的无量纲挠度、速度和应力变化曲线。从图12(a)无量纲挠度曲线可知,由冲击因子C3设计的模型试验的塑性变形挠度与原型试验误差最小,误差最大处出现在曲线的后半段,为4.3%;从图12(b)无量纲速度曲线和图12(c)无量纲应力曲线可知,两种冲击因子对应试验模型的速度曲线和应力曲线只有依据冲击因子C3设计的试验模型的曲线趋势与原型工况保持一致,依据冲击因子C2设计的模型试验速度和应力曲线趋势与原型一致性较差,这是因为其试验载荷特性与原型存在一定差异造成的。

图11 当λ=1/3时,平板结构应力云图Fig.11 When λ=1/3, the stress cloud diagram of the flat structure

将图12中原型与模型的挠度、速度和应力曲线数据根据式(33)进行计算得到关于曲线在统计区间内的Spearman秩相关系数,如表7所示。表7中,ry,rV和rS分别表示无量纲挠度、速度和应力曲线的相关系数。

表7 当λ=1/3时,平板模型试验与原型数据的秩相关系数

由表7可知,当缩尺比λ=1/3时,依据C3设计的缩比模型试验在无量纲挠度、速度和应力曲线的相关系数最大,表明依据冲击因子C3设计的缩比模型试验可以很好的评估原型试验的毁伤效果,从统计学的角度进一步验证了冲击因子C3的可靠性。对于平板模型,当缩尺比λ=1/3时,依据冲击因子C3设计的模型试验能很好地转换到原型试验。

(3) 当λ=1/6时,平板模型数值试验结果分析

当缩尺比λ=1/6时,分别依据冲击因子C2和C3设计的工况8和工况9在同时刻的应力云图如图13所示。图14为结构的无量纲挠度、速度和应力变化曲线。从图14(a)无量纲挠度曲线可知,由冲击因子C3设计的模型试验的塑性变形挠度与原型试验误差最小,误差最大处出现在曲线的后半段,为5.9%;从图14(b)无量纲速度曲线和图14(c)无量纲应力曲线可知,两种冲击因子对应工况的速度和应力曲线只有依据冲击因子C3设计的模型试验曲线趋势与原型试验一致,依据冲击因子C2设计的模型试验速度和应力曲线趋势与原型一致性较差,这是因为其的试验载荷特性与原型存在一定差异造成的。

图13 当λ=1/6时,平板结构应力云图Fig.13 When λ=1/6 the stress cloud diagram of the flat structure

图14 当λ=1/6时,平板结构中心点的挠度、速度和应力曲线Fig.14 When λ=1/6, the deflection, velocity and stress curve of the center point of the flat structure

将图14中原型与模型的挠度、速度和应力曲线数据根据式(33)进行计算得到关于曲线在统计区间内的Spearman秩相关系数,如表8所示。表8中,ry,rV和rS分别表示无量纲挠度、速度和应力曲线的相关系数。

表8 当λ=1/6时,平板模型试验与原型数据的秩相关系数

表8给出了,当缩尺比λ=1/6时,依据C3设计的缩比模型试验在无量纲挠度、速度和应力曲线的相关系数最大,表明依据冲击因子C3设计的缩比模型试验可以很好的评估原型试验的毁伤效果,从统计学的角度进一步验证了冲击因子C3的可靠性。对于平板模型,当缩尺比λ=1/6时,依据冲击因子C3设计的模型试验能很好地转换到原型试验。

3.3.2 板架模型数值试验结果分析

通过3.3.1节中对平板模型试验数据的处理,发现根据不同缩尺比设计的试验数据相似,板架模型试验数据也存在这样的相似性,故下面将只对缩尺比λ=1/2时各试验工况的试验结果进行详细分析。

分别依据冲击因子C2和C3设计的工况12和工况13在同时刻的应力云图如图15所示,当冲击波作用在结构上时,依据冲击因子C3设计的模型试验应力分布与原型相似。图16为结构的无量纲挠度、速度和应力变化曲线。从图16(a)无量纲挠度曲线可知,由冲击因子C2对应模型试验的变形挠度曲线趋势与原型试验的差异性较大。由冲击因子C3设计的模型试验的变形挠度曲线趋势与原型试验的,同时其塑性变形挠度与原型试验误差最小,为5%;从图16(b)无量纲速度曲线和图16(c)无量纲应力曲线可知,三种冲击因子对应工况的速度和应力曲线只有依据C3设计的模型试验曲线趋势与原型一致,依据冲击因子C2设计的模型试验的速度曲线和应力曲线趋势与原型一致性较差。依据冲击因子C3设计的模型试验的板架中心点挠度、速度变和应力的变化过程与原型变化趋势相同,在曲线后半段均出现偏差,误差在工程应用允许范围内。

图15 当λ=1/2时,板架结构应力云图Fig.15 When λ=1/2, the stress cloud diagram of the plate frame structure

图16 当λ=1/2时,板架结构中心点的挠度、速度和应力曲线Fig.16 When λ=1/2, the deflection, velocity and stress curve of the center point of the flat structure

将图16中原型与模型的挠度、速度和应力曲线数据根据式(33)进行计算得到关于曲线在统计区间内的Spearman秩相关系数,如表9所示。表9中,ry,rV和rS分别表示无量纲挠度、速度和应力曲线的相关系数。

表9 当λ=1/2时,板架模型试验与原型数据的秩相关系数

由表9可知,当缩尺比λ=1/2时,依据C3设计的缩比模型试验在无量纲挠度、无量纲速度和无量纲应力曲线的相关系数最大,表明依据冲击因子C3设计的缩比模型试验可以很好的评估原型试验的毁伤效果,从统计学的角度进一步验证了冲击因子C3的可靠性。

3.3.3 舱段模型数值试验结果分析

通过3.3.1节和3.3.2节中对平板和板架模型试验数据的处理发现,根据不同缩尺比设计的试验数据相似,舱段模型试验数据也存在这样的相似性,故下面将只对缩尺比λ=1/2时各试验工况的试验结果进行详细分析。

分别依据冲击因子C2和C3设计的工况22和工况23在同时刻的应力云图如图17所示,当冲击波作用在结构上时,依据冲击因子C3设计的工况应力分布与原型工况相似。舱段结构整体尺寸较大,冲击响应范围也较大,但舱段结构整体响应较小,故取舱段结构临近中心点的板格变形挠度数据,取爆心与舱段外底最短连线测点的变形速度和应力数据,按照式(30)、式(31)处理后得到图18为结构的无量纲挠度、速度和应力变化曲线。从图18(a)无量纲挠度曲线可知,依据式(26)表示的冲击因子C3设计的模型试验的塑性变形挠度数据与原型工况误差最小,为5%,且挠度曲线变化趋势相同;从图18(b)无量纲速度曲线和图18(c)无量纲应力曲线可知,两种冲击因子对应模型试验的速度和应力曲线只有依据冲击因子C3设计的模型试验曲线趋势与原型保持一致,依据冲击因子C2设计的模型试验速度曲线和应力曲线趋势与原型试验一致性较差。依据冲击因子C3设计的模型试验的板架中心点挠度、速度和应力的变化过程与原型试验数据变化趋势相同,误差在工程应用允许范围内。

图17 当λ=1/2时,舱段结构应力云图Fig.17 When λ=1/2, the structural stress cloud diagram of the cabin section

图18 当λ=1/2时,舱段结构中心点的挠度、速度和应力曲线Fig.18 When λ=1/2, the deflection, velocity and stress curve of the center point of the cabin structure

将图18中原型与模型的挠度、速度和应力曲线数据根据式(33)进行计算得到关于曲线在统计区间内的Spearman秩相关系数,如表10所示。表10中,ry,rV和rS分别表示无量纲挠度、速度和应力曲线的相关系数。

表10 当λ=1/2时,舱段模型试验与原型数据的秩相关系数

如表10所示,当缩尺比λ=1/2时,依据冲击因子C3设计的工况在无量纲挠度、速度和应力曲线的相关系数最大,表明冲击因子C3对原型工况的毁伤效果评估精度较高,从统计学的角度进一步验证了冲击因子C3的可靠性。

3.3.4 数值试验结果小结

通过对比板、板架、舱段模型在不同缩尺比情况下结构响应中的无量纲挠度、速度、应力分析以及数学统计相关性分析,依据冲击因子C3设计的模型试验结果可以很好地转换到原型试验,相较于C2设计的模型试验预报精度更高。随着缩尺比的增大,两种冲击因子的模型试验与原型试验的毁伤数据一致性精度都存在下降的趋势,依据冲击因子C3设计的缩比模型试验精度变化较小,依据冲击因子C2设计的模型试验精度下降的更显著,从而验证了冲击因子C3的有效性和较传统冲击因子的优越性。这是因为由式(13)可知传统冲击因子C2定义式中没有关于目标结构特性的物理量,在缩比模型试验中没有对目标结构尺寸(依据式(29))进行几何缩比处理,而C3定义中考虑了当缩比试验模型设计中同时考虑爆源相似性和目标结构特性。

4 舰船典型局部结构试验验证

为了验证依据新型冲击因子C3设计舰船结构模型在水下非接触爆炸条件下是否可以很好的预报原型试验,本文根据某型舰船的双层底板架结构和船舯部的舱段结构,设计了双层底板架试验模型和舱段试验模型进行水下爆炸冲击毁伤试验,使用数值与试验相结合的验证方法,分别依据式(12)、式(13)和式(26)表示的冲击因子C1,C2和C3设计了不同缩尺比下的模型试验。

4.1 双层底板架结构缩比模型试验

4.1.1 双层底板架结构缩比模型试验方案设计

根据某型舰舱段结构尺寸,选取舰船中部的双层底结构设计板架结构模型,结构尺寸分别为:外底2.16 m×1.92 m×0.003 m,内底2.16 m×1.92 m×0.002 m,内、外底之间纵横两个方向上各均布6个肋板,将内、外底分别格成6×6的36个小板格,每个小板格的长宽为0.36 m×0.32 m,主肋板厚为0.002 m,纵向肋板厚为0.003 m,双层底高为0.2 m,内外底板在纵向方向上均布18根小加强筋,加强筋采用扁钢。试验采用球形装药(TNT),装药布置在模型中心纵桁与肋板相交处的正下方,装药质量(Wp)为2 kg,爆距(Rp)为1.5 m。

依据冲击因子定义,设计缩比模型试验,具体模型试验数据如表11所示。表11中:δm5和δm6表示双层底内、外底厚度;Dm3和Dm4分别表示内外底上的型材尺寸;Wm和Rm分别表示试验模型的装药(TNT)质量和爆距,同时Wm和Rm以及模型尺寸依据式(29)设计得到,模型试验中结构采用将内、外底的边界条件为四周简支,双层底模型结构布置图如图19所示。

表11 双层底板架结构缩比模型试验工况表Tab.11 Working condition table of scaled-down test of double-layer floor frame structure model

图19 双层底板架结构示意图(mm)Fig.19 The structure diagram of the double-layer floor frame structure model (mm)

4.1.2 双层底板架模型试验结果分析

如图20所示,双层底试验模型由于试验场地的限制在试验水池中无法固定,且其质量不大,无法模拟预设的边界条件。为此,在在双层底试验模型的上方0.4 m处设置一个平台,然后在平台上方建立水密舱室结构。另外在双层底模型外底两侧设置翼板是为了增大模型的附加阻尼,减小双层底模型刚体运动。双层底试验模型在原型载荷作用下产生塑性大变形,原型试验得到双层底模型外底中心点的变形挠度为0.136 m,原型试验毁伤变形如图21所示。

图20 试验人员吊装模型Fig.20 The experimenter hoisted the model

图21 双层底板架外底变形图Fig.21 Experimental Deformation Diagram of Outsole of Double Floor Frame

第3章通过数值验证时发现,根据不同缩尺比设计的试验数据相似,双层底模型试验数据也存在相似性,故下面将只对缩尺比λ=1/2时各试验工况的试验结果进行详细分析。取双层底外底中心点的变形挠度、变形速度和应力数据,按照式(30)、式(31)进行无量纲化处理后,得到无量纲挠度、速度和应力曲线,如图22所示。

图22 当λ=1/2时,板架结构中心点的挠度、速度和应力曲线Fig.22 When λ=1/2, the deflection, velocity and stress curve of the center point of the plate frame structure

从图22(a)无量纲挠度曲线可知,当缩尺比λ=1/2时,分别依据冲击因子C2和C3设计的模型试验塑性变形挠度与试验数据的误差分别为73.5%和7.6%。从图22(b)无量纲速度曲线和图22(c)无量纲应力曲线可知,两种冲击因子对应工况的速度和应力曲线只有依据C3设计的模型试验曲线趋势与原型保持大致一致,模型试验与原型试验存在一定的误差。产生误差的主要原因是由于数值试验中的边界条件为理想边界条件,试验中难以实现,同时在结构缩比过程中结构等效强度发生变化,所以模型试验结果与原型试验结果存在一定的误差。除了上述原因外,本试验的爆心与结构中心点和边缘点(短边中点)的夹角为35°,由式(15)可知此时水下爆炸冲击波并不能很好的近似为平面波。从数学图形的角度分析,依据新型冲击因子C3设计的模型试验与原型试验在结构动响应方面的误差在工程应用允许范围内,模型试验仍可以较好的评估原型试验的毁伤结果。

将图22中原型与模型的挠度、速度和应力曲线数据根据式(33)进行计算得到关于曲线在统计区间内的Spearman秩相关系数,如表12所示。表12中,ry,rV和rS分别表示无量纲挠度、速度和应力曲线的相关系数。

表12 当λ=1/2时,双层底板架模型试验与原型数据的 秩相关系数

如表12所示,当缩尺比λ=1/2时,依据C3设计的缩比模型试验在无量纲挠度、无量纲速度和曲线的相关系数最大,表明依据冲击因子C3设计的缩比模型试验依旧可以较好地评估原型试验的毁伤效果,从统计学的角度进一步验证了冲击因子C3的可靠性。

4.2 舱段模型试验

4.2.1 舱段模型试验方案设计

为了进一步验证新型冲击因子对于复杂舰船结构在水下爆炸缩比模型试验中的正确性,依据某型船设计了1∶1舱段试验模型,模拟水面舰船在非接触爆炸作用下的毁伤效果。模型沿船长方向取5倍肋距、沿船宽方向取船宽的一半。模型高为3.85 m,型宽为8.2 m,长为7.5 m,底部板架结构是典型的纵向式结构,其中横向构件与纵向构件的强度相同,由五根纵向构件和五根横向构件均布构成,纵向构件间距是1.6 m,横向构件间距是1.5 m,如图23、图24所示。

图23 舱段原型结构正视图(m)Fig.23 Front view of cabin model structure (m)

图24 舱段原型结构侧视图(m)Fig.24 Side view of cabin model structure (m)

为研究典型舱段结构水下非接触爆炸的冲击毁伤特性,试验采用球形装药(TNT),当量(Wp)为8 kg,装药布置在舱段结构中间实肋板正下方,爆距(Rp)为5.9 m。基于冲击因子定义对试验模型进行缩比仿真试验,具体试验工况如表13所示。表13中,Wm和Rm分别表示试验模型的装药(TNT)质量和爆距,同时Wm和Rm以及模型尺寸依据式(29)设计得到,模型试验中结构采用将上板架的边界条件为四周简支。

4.2.2 舱段模型试验结果分析

基于分析冲击范围内板与实肋变形的差异性和试验数据采集的便捷性,将舱段双层底结构从中内龙骨至舭部分划分成16个板格区域,如图25所示。舱段试验模型在原型载荷作用下产生塑性变形,试验得到舱段模型外底板上6号板格中心点的变形挠度为0.016 3 m,原型试验毁伤变形如图26所示。

图25 外底板各板格标号Fig.25 Marking of each panel of the outer bottom plate

图26 舱段双层底外底变形图Fig.26 Experimental deformation diagram of double bottom outsole at the bottom of the cabin

第3.3.3节通过试验验证时发现,根据不同缩尺比设计的试验数据相似,舱段模型试验数据也存在同样的情况,故下面将只对缩尺比λ=1/2时各试验工况的试验结果进行详细分析。原型试验爆心位置即在6号板格中心点的正下方,故提取该点的变形挠度、变形速度和应力数据,按照式(30)、式(31)进行无量纲化处理后,得到无量纲挠度、速度和应力曲线,如图27所示。

图27 当λ=1/2时,舱段6号板格中心点的挠度、速度和应力曲线Fig.27 When λ=1/2, the curve of deflection, velocity and stress at the center point of compartment panel 6

从图27(a)无量纲挠度曲线可知,当缩尺比λ=1/2时,分别依据冲击因子C2和C3设计的模型试验6号板格中心点的塑性变形挠度值与试验数据的误差分别是72.7%和16.7%。从图27(b)无量纲速度曲线和图27(c)无量纲应力曲线可知,依据冲击因子C3设计的模型试验与原型误差最小,产生误差的主要原因:仿真计算模型边界条件为简支,与试验实际边界条件不太符合;缩比模型梁的截面尺寸也依据式(29)采用完全几何缩比,缩比后梁的截面特性发生变化,结构等效强度发生变化,从缩比试验得到的挠度曲线峰值(弹塑性变形峰值)较试验结果误差较大,也能反映出模型与原型的结构等效强度不同。虽然缩比试验结果与试验结果存在一定误差,通过对比依据冲击因子C2和C3设计的模型试验6号板格中心点变形挠度、速度和应力曲线与原型试验结果的差异性,发现依据冲击因子C3设计的试验模型试验结果数值误差较小,同时曲线变化趋势与原型保持一致,表明依据冲击因子C3设计的缩比模型试验中可以很好地评估原型试验,具有较好的工程应用价值。

将图27中原型与模型的挠度、速度和应力曲线数据根据式(33)进行计算得到关于曲线在统计区间内的Spearman秩相关系数,如表14所示。表14中,ry,rV和rS分别表示无量纲挠度、速度和应力曲线的相关系数。

表14 当λ=1/2时,实船舱段模型试验与原型数据的 秩相关系数

如表14所示,当缩尺比λ=1/2时,依据式(26)表示的冲击因子C3设计的工况在无量纲挠度、无量纲速度和无量纲应力曲线的相关系数最大,表明冲击因子C3对原型工况的毁伤效果评估精度较高,从统计学的角度进一步验证了冲击因子C3的可靠性。

综上,通过对双层底板架结构和舱段模型在不同缩尺比条件下的无量纲挠度、速度和应力分析以及数学统计相关分析,与数值验证的结论一致:依据C3设计的缩比模型在预报原型结果的精度比传统冲击因子C2预报的精度更高,适用性更好,进一步验证了本文提出的考虑目标结构特性的新型冲击因子C3较传统冲击因子具有优越性。

5 结 论

本文结合数学几何条件和结构表面整体冲量对比法提出了当冲击波达到结构中心点与结构边缘点的相对时间差值系数α=0.1(如式(17))时可以更好地表征水下爆炸冲击波的平面波效应。通过结合单值物理量相似和冲击波输入特征,基于多个单值物理量的量纲分析提出了一种新型冲击因子C3。依据传统冲击因子C1,C2和新型冲击因子C3设计模型试验,以结构变形挠度、变形速度和测点应力为考察量,对多种缩尺比情况下模型试验与原型试验塑性大变形范围内的毁伤相似性进行验证和讨论,得到了以下结论:

(1) 本文结合数学几何理论和结构表面整体冲量作用提出了α=0.1时可以更好地表征水下爆炸冲击波的平面波效应。

(2) 传统冲击因子C1和C2定义中没有考虑单值物理量相似,不满足单值条件中的几何条件和边界条件,试验模型冲击波输入特征与原型不同,预报原型毁伤效果存在一定的局限性。冲击因子C1是基于超压峰值相等,没有考虑爆炸冲击波能量的影响,当目标结构满足相似要求时,此时冲击因子C1形式与C3相同,而冲击因子C2是基于冲量相等,没有考虑超压峰值的影响,只有当冲击波满足平面波效应时,结构变形挠度峰值 的预报误差在10%以内。

(3) 根据本文提出的水下爆炸平面波效应条件,结合单值物理量相似和冲击波输入特征推导的新型冲击因子C3, 通过数值试验和模型试验分析讨论,表明依据C3设计的缩比模型试验能够较好的转换到原型试验。