间谐波激励下铁心振动噪声特性研究

2023-12-01李金博

振动与冲击 2023年22期

邢琳, 张帅, 李燕, 吴鹏, 甘浩, 李金博

(1. 国网河北省电力有限公司经济技术研究院,石家庄 050023;2. 华北电力大学河北省输变电设备安全防御重点实验室,保定 071066)

近年来随着大量电力电子装置接入到电网之中,导致电网中的电压或电流中存在基波非整数倍的频率分量,也即间谐波[1-2],间谐波的存在使得铁心快速饱和,同时励磁电流大幅畸变,进而导致设备使用寿命减少,噪声增大[3],严重影响居民的身心健康,危害到电网的安全运行稳定。

目前,国内外专家学者对变压器振动噪声问题开展了广泛的研究,杜海泉[4]测量了不同谐波激励下变压器铁心振动特性,结果发现铁心振幅对三次谐波更为敏感。赵莉华等[5]通过改变变压器负载的谐波畸变率研究了谐波对变压器振动特性的影响。吴晓文等[6]搭建了位于半消声室内的变压器噪声试验平台,并测量了施加谐波激励的铁心噪声信号,研究得到噪声水平随着负载谐波含量的提高而增大。李慧奇等[7]研究了间谐波激励对变压器铁心励磁特性影响。赵锦涛[8]对不同间谐波源进行了建模,同时对间谐波激励下铁心励磁性能进行了研究,发现低频间谐波对变压器铁心励磁性能影响更大。上述文献主要进行了谐波激励下铁心振动噪声试验及间谐波激励下的励磁试验,关于含低频低含量间谐波激励对变压器铁心振动噪声特性的影响研究较少。

本文针对间谐波激励下变压器的振动与噪声问题,首先搭建了含任意间谐波铁心振动和噪声试验平台,并建立了磁-结构力场-声场多物理耦合有限元三维模型,对试验结果与计算结果进行对比分析,总结低频低含量间谐波对变压器铁心噪声值的影响规律,本文研究可为铁心制作提供依据。

1 变压器铁心振动-噪声特性试验

1.1 试验电路图及激励施加方法

搭建了产生任意间谐波激励变压器振动噪声试验平台,试验设备图如图1所示,基于电工钢片制作而成的叠片铁心进行变压器振动噪声试验,研究铁心在含工频及不同间谐波激励下的振动噪声特性。试验电路图如图2所示。

图1 试验设备图Fig.1 Experimental equipment

图2 试验电路图Fig.2 Experimental circuit diagram

本次试验施加含量在5%,频率为2 Hz,5 Hz,10 Hz等次谐波激励,研究间谐波的频率f2和在基波中的含量m对变压器铁心模型的影响,通过编辑信号发生器,对变压器铁心励磁线圈施加含间谐波的电压激励,如式(1)所示

v(t)=V1[sin(2πf1t)+msin(2πf2t)]

(1)

式中:V1为基波电压幅值;f1为基频频率50 Hz;f2为间谐波频率;m为间谐波幅值与基波幅值的比值。

1.2 间谐波分量成因分析

基于搭建的试验平台进行铁心振动试验,使用高分辨率的LV-S01单点激光测振仪和DH-5902数据记录分析系统测量铁心的振动位移,当铁心模型施加激励后产生磁场,铁心由于磁致伸缩效应等原因会产生振动,选择铁心铁轭上表面的中心点和侧点进行测量,振动试验现场图及测点分布如图3所示。

图3 振动试验现场及测点分布图Fig.3 Vibration experiment site and measuring point distribution map

对测量得到的速度信号进行频谱分析发现:单含有单一间谐波频率的电压激励下,频谱中含有大量间谐波分量,分布在基波的各次谐波附近且成对出现。为进一步研究间谐波激励下铁心振动频谱中间谐波分量的产生规律,对其进行了定量分析,考虑铁心磁通-应变特性的解析模型,结合磁致伸缩特性曲线[9]式(2)与磁通密度式(1)得到关于铁心振动与激励频率关系式(4),同时忽略方向影响。

(2)

(3)

(4)

考虑铁心振动只与角频率ω1和ω2有关,忽略其他参数影响,可以发现振动量关于变量的幂次数为偶数。对与频率相关的角频率ω1和ω2进行分析,对通项分析可得

(5)

对第一项通过三角函数降幂公式分析

(6)

可以看出在振动频谱中会存在基波ω1的偶次谐波(2n)频率,同理对等式第n项分析也可得存在间谐波频率ω2的偶次谐波频率,如图4中存在的100 Hz,200 Hz等频率。

图4 间谐波激励下振动频谱分析Fig.4 Vibration spectrum analysis under interharmonic excitation

对第二项分析

(7)

结果存在(2m-1)ω1±ω2项,所以在含间谐波激励下铁心振动频谱中存在(2m-1)f1±f2项,即奇次谐波相减或相加所加间谐波频率,如图4(a)中48 Hz,52 Hz,图4(b)中43 Hz,57 Hz等频率。同理对i=3项进行分析时还会出现(2m-1)f1±3f2, 即与奇次谐波相减或相加奇数次间谐波频率,如图4(a)中44 Hz,56 Hz等频率。

对第三项进行分析

(8)

结果项中存在2mω1±2ω2,因此铁心振动频谱中存在2mf1±2f2项,即偶次谐波相减或相加两倍间谐波频率,如图4(a)中96 Hz,104 Hz,图4(b)中86 Hz,114 Hz等频率。同理对i=4项进行分析时还会出现2mf1±4f2,即与偶次谐波相减或相加偶数次间谐波频率,如图4(a)中92 Hz,108 Hz等频率。

综上所述,含间谐波激励下振动频谱中间谐波分量频率与激励所含间谐波频率关系总结如下

(9)

式中:fj为变压器励磁电流主要间谐波的频率;f1为基波50 Hz;f2为激励所含间谐波频率。

由于环境中干扰信号的叠加以及电工钢片非线性特征导致存在小于50 Hz的低频干扰分量[10]。测量设备中的高通滤波器将低频干扰信号进行滤除,所以低频部分间谐波的分布规律不明显,但是不影响50 Hz附近及以上频率的分析。间谐波分量分布规律如图4所示,从图4(a)可看出含2 Hz激励下在基波、三次和五次谐波附近的间谐波与谐波相差2 Hz,6 Hz等频率,在二次、四次、六次谐波附近的间谐波与谐波相差4 Hz,8 Hz等频率。

1.3 噪声结果分析

变压器铁心由于自身振动进而产生噪声,为了研究含间谐波激励下变压器铁心的噪声特性,在试验室环境中对铁心噪声进行了测量。声级计探头测点选取参考标准GB/T 1094.10—2003中的变压器声级测定部分,按要求测量的轮廓线距离基准面为0.3 m,每个测点的测量时间不低于30 s。为了排除环境噪声对测量结果的干扰,将铁心单独放置于具有隔声性能的试验室中进行测量。最后根据声级计算公式获得不同激励下变压器的噪声水平,噪声测点分布图如图5所示。

图5 噪声测点分布图Fig.5 Distribution of noise measuring points

图6展示了不同激励下围绕变压器测量轮廓线不同位置处测点得到的A计权声压级,可以看出在测量点5处得到的声压级大于其他测点,这是由于铁心上轭处振动较为剧烈引起的。其他不同测点处的声压级差异较小,基本在某一固定值上下波动。铁心运行过程所测得噪声均大于背景噪声,但由于两者声级值之差小于10 dB,测量结果会受到背景噪声的干扰而无法准确得到变压器铁心的噪声值。因此需要对被测声源运行状态下的总体噪声测量结果进行修正[11],首先将不同位置的测量点所得的A计权声压结果代入式(10),可以分别计算出环境背景噪声及设备运行时噪声的平均A计权声压级LPA[12]。

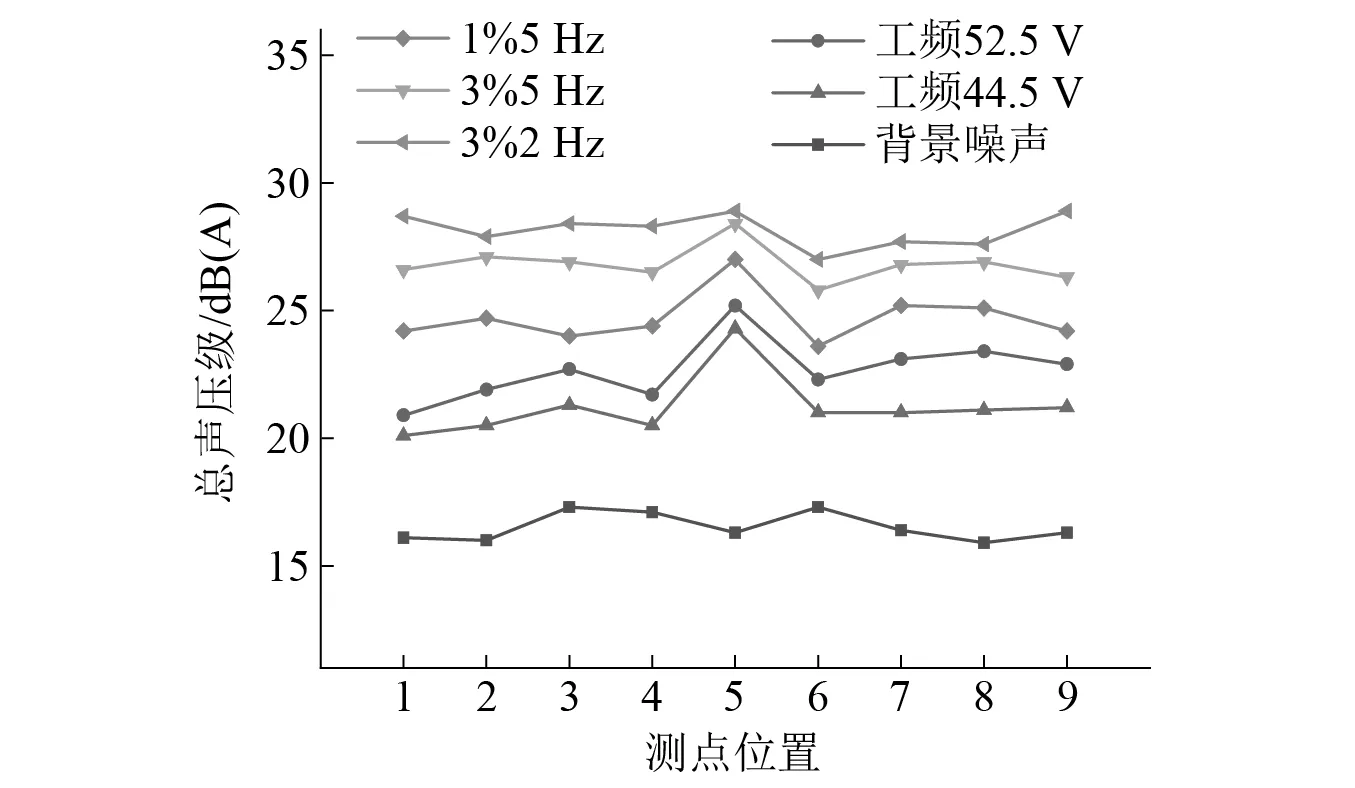
图6 不同测点位置噪声分布Fig.6 Noise distribution of different measuring points

(10)

式中:n为测量点个数;i为测点序号;LAi为对应位置处测点上所得的A计权声压级。

根据式(11)来修正背景噪声对所测结果的影响。

LPB=10lg(100.1LPA-100.1LBA)-K

(11)

式中:LPA和LBA分别为试验中求得的设备和背景噪声的平均A声级;K与材料吸声系数与测量场地面积有关,由于实验室中的吸波材料具有吸声性能,因此K对结果的影响可以忽略。

根据式(10)和式(11)计算后得到的随间谐波频率变化的变压器噪声修正值,如图7所示。由图7可知,在基波为60.5 V时,无间谐波激励下变压器铁心A计权噪声级为24.2 dB,随着间谐波频率的降低,噪声A声级逐渐增加,当间谐波频率为2 Hz时,变压器铁心A声级达到34.5 dB,增加了10.3 dB。随着电压降低,声压级下降,但其变化规律基本一致。从两条曲线可以观察出在频率较低的情况下噪声增长率较快。

图7 修正后含间谐波激励下噪声随频率变化Fig.7 Noise variation with frequency under excitation with interharmonics after correction

在对噪声测量评价中,常使用1/3倍频程将音频分成不同频段来反映噪声源的频谱特性,根据国家标准HJ 706—2014环境噪声监测中的噪声测量值修正部分,可先得到测量背景噪声的各个倍频带的声压级,再根据式(11)对每个倍频带测量值进行修正。如图8所示为测点5位置处,基波52.5 V 下无间谐波和含3%5 Hz 间谐波的频谱分布。

图8 不同激励下噪声1/3倍频程频谱对比Fig.8 Comparison of noise 1/3 octave frequency spectrum under different excitations

从图8可以看出,不同激励下变压器铁心噪声声压级随频率的变化规律相似,都以100 Hz,200 Hz,300 Hz倍频带为主要峰值,超过500 Hz部分的频率分量较小,明显表现出低频频谱特征。在含间谐波激励下,主要频率对应的声压级都有所降低,但主要还是集中在要集中在100～500 Hz频率之间。

2 模型建立及计算结果分析

2.1 仿真模型建立

通过COMSOL有限元软件对变压器铁心进行仿真分析,建立三维模型。铁心底部施加固定约束,在磁场部分于铁心处设置电工钢材料交流磁化特性单值曲线,如图9所示;设置磁致伸缩特性曲线,如图10所示。铁心外部为空气域,为了优化计算速度将铁心模型简化为整体结构,同时忽略硅钢铁心的涡流效应,将线圈视为整体进行均匀化处理。空气域部分采用较粗化的四面体网络,外围采用多层网络吸收传播声波以抑制外部声场边界产生的反射,模型网络剖分图如图11所示。

图9 磁化曲线Fig.9 Netization curve

图10 磁致伸缩曲线Fig.10 Magnetostriction curve

图11 网络剖分图Fig.11 Network breakdown

铁心计算模型参数如表1所示。

表1 计算模型参数Tab.1 Calculation model parameters

2.2 噪声仿真结果与分析

基于计算模型电磁场与振动的分析基础,将铁心的振动位移数据加载到声场模型当中,计算得到变压器铁心近场的相邻步长(0.5 ms)声压分布,如图12所示。从图12中可以看出,声压的扩散分布关于变压器的轴方向对称,从铁心表面产生后向四周均匀扩散且逐渐减小,符合声波在空气介质中传播的趋势。

图12 相邻步长近场区域声压分布Fig.12 Sound pressure distribution in the near-field region at different times

工频及含间谐波激励下变压器模型的声压级分布如图13所示。从图13中可以看出,在底部固定约束情况下声压级在铁心上方位置处数值较大,噪声向上铁轭方向传播,下铁轭方向的噪声则相对较小;水平方向上的声压级相较于竖直方向上的声压级数值较小,随着声波传播声压减小声压级也随之降低。相比于工频激励,含间谐波激励下铁心由于振动加剧,产生的噪声也随之增加。

为分析不同激励下变压器铁心的噪声特性,对计算模型得到的声学时域信号进行快速傅里叶变换分解,得到在相同激励下铁心上方测点5处的100～500 Hz之间的等效A计权声压级倍频带,如图14所示。从图14中可以看出,计算得到的A计权声压级在低频段随频率的分布规律与试验测量结果大致相同;计算结果在80～160 Hz部分大于实际测量结果,在200～500 Hz倍频带部分小于实际测量结果,这是因为变压器铁心在实际运行状态下,各次谐波互相影响,声波中的频率成分可能与变压器结构发生了共振;此外,铁心材料磁致伸缩特性模型非线性的影响也是计算中产生误差的原因。

图14 不同激励下噪声频谱计算结果对比Fig.14 Comparison of noise spectrum calculation results under different excitations

不同激励及不同测点位置处的实测噪声与计算结果数据,如表2所示。从表2中可以看出,计算结果与实测值基本吻合,验证了计算模型的有效性。在噪声计算中造成误差的原因有:在对振动计算中简化了变压器模型实际结构,将铁心视为整体没有考虑叠片之间振动对噪声的影响等。经过声场分析计算可将变压器周围声压级的大小分布进行可视化,并分析铁心产生的噪声频带特性,可以在设计阶段预测变压器产品的噪声特性,有利于缩短设计制造周期,降低模型试验成本。