基于Stacking模型融合的高性能混凝土强度预测方法

2023-12-01胡以婵谢灿荣解威威翁贻令罗雪霜

硅酸盐通报 2023年11期

胡以婵,梁铭,谢灿荣,解威威,翁贻令,池浩,彭浩,罗雪霜

(广西路桥工程集团有限公司,南宁 530011)

0 引言

混凝土是一种使用广泛的建筑材料,其性能直接影响建筑物的结构安全、使用寿命和维护成本等关键指标。其中,混凝土强度是最重要的指标之一,直接影响建筑物的承载能力和稳定性[1-2]。传统确定混凝土强度的方法通常是基于基准混凝土配合比,通过保持水胶比或砂率不变,不断调整胶凝材料和骨料的组合,这种方法不仅耗费大量原材料,浪费大量的人力和时间,且存在偏差大、效率低的问题[3-4],难以对混凝土的强度进行快速准确的评估。由此可见,实现迅速且准确的混凝土抗压强度预测尤为重要[5-6]。

近年来,国内外研究人员在混凝土抗压强度预测领域积极探索,许多学者已开始使用机器学习的方法来研究混凝土抗压强度与相关因素之间的关系[7-11]。对于再生骨料混凝土,Yuan等[12]采用了梯度提升(gradient boosting, GB)和随机森林(random forest, RF)算法,结果表明RF具有较好的预测效果;而Shang等[13]采用了决策树(decision tree, DT)和自适应增强(adaptive boosting, AdaBoost)算法对混凝土强度进行预测,其中AdaBoost模型具有更高的预测精度。关于稻壳灰混凝土,Iftikhar等[14]采用遗传算法(genetic algorithm, GA)和RF进行混凝土强度预测,结果表明GA具有更高的预测精度。针对高性能混凝土,Feng等[15]采用AdaBoost集成学习方法进行强度预测,并采用一组新的数据集来验证该模型的泛化性能,结果表明该模型具有较高的精度和良好的泛化性能;Asteris等[16]采用人工神经网络(artificial neural network, ANN)、线性和非线性多元自适应回归样条(linear multivariate adaptive regression splines, MARS-L; nonlinear multivariate adaptive regression splines, MARS-C)、高斯过程回归(gaussian process regression, GPR)和极大极小概率机回归(minimax probability machine regression, MPMR)四种传统机器学习(conventional machine learning, CML)模型,将CML模型的预测结果输出并进行组合,再利用人工神经网络(artificial neural network, ANN)进行训练,构建混合集成模型(hybrid ensemble model, HENSM),结果表明HENSM具有更高的预测精度。Farooq等[17]采用个体学习器和集成学习器,总体上RF和DT模型在拟合数据时表现出较高的鲁棒性,并且误差较小。在钢纤维增强混凝土方面,Kang等[18]采用11种算法进行强度预测,并通过K-fold验证,防止模型过拟合,结果表明极端梯度提算法(extreme gradient boosting, XGBoost)的预测精度最高;而马高等[19]采用反向传播神经网络(back propagation neural network, BPNN)对纤维增强混凝土进行强度预测,结果表明BPNN能够很好地挖掘输入输出参数的数据信息,得到高精度的预测模型。在其他类型的混凝土强度预测方面,国内外学者也运用机器学习的方法进行了一系列研究,并在预测效果上取得一定的成果。其中,Nguyen等[20]采用深层神经网络(deep neural network, DNN)和深残余网络(residual network, ResNet)预测粉煤灰地质聚合物混凝土的抗压强度;韩建军等[21]等采用BPNN对垃圾飞灰混凝土进行抗压强度预测模型;徐潇航等[22]采用多层感知机回归(multi-layer perceptron, MLP)模型、支持向量机(support vector machine, SVR)模型与RF模型对三峡大坝混凝土强度进行预测;梁宁慧等[23]采用回归树算法(regression tree, RT)、SVR和ANN对经高温后的聚丙烯纤维混凝土进行强度预测。韩斌等[24]采用粒子群算法(particle swarm optimization, PSO)对ANN进行优化,实现对湿喷混凝土强度的高精度预测;汪声瑞等[25]等通过天牛须搜寻算法(beetle antennae search, BAS)训练MLP,并与混合复杂进化方法(shuffled complex evolution, SCE)、多元宇宙优化算法(multi-verse optimizer, MVO)两种MLP耦合算法开展混凝土强度预测;李杨等[26]则提出了一种基于分类与回归树(classification and regression tree, CART)算法优化SVR回归算法的预测方法,用于提高混凝土抗压强度的预测精度。

综上可知,国内外学者针对不同类型的混凝土已开展了大量的强度预测模型研究。其中,高性能混凝土因优良的耐久性、工作性、力学性能、适用性、体积稳定性和经济合理性具有广阔的应用前景[27],目前在公路[28]、铁路[29]、房屋建筑[30-31]及水运工程[32-33]等领域得到了广泛应用。然而,在已有研究中主要关注单个学习器对高性能混凝土性能的预测情况,在综合考虑多种模型的集成上少有研究,如何充分利用单个学习器的优势,提高模型的预测精度和泛化性能,成为建筑行业混凝土高质量发展的重点。

本研究将人工智能技术XGBoost算法、CatBoost算法、MLP算法、RF算法与集成学习方式有效结合,提出一种基于Stacking模型融合的高性能混凝土强度预测方法。首先,对收集到的1 030组高性能混凝土抗压强度数据开展数据预处理,研究单一机器学习算法对强度的预测精度;其次,在Stacking集成框架下,建立了多种差异化模型融合的强度预测模型并采用新的103组高性能混凝土数据集来验证该模型的泛化性能;最后,采用SHAP值(shapely value)对模型进行可解释性分析。结果表明:选用XGBoost和RF融合的stacking集成模型预测精度和泛化性能较好,可解释分析显示最重要的输入特征变量是龄期和水泥,说明模型内在的预测逻辑与工程实践的经验较吻合,具有较高的合理性与可靠度。

1 算法原理介绍

1.1 Stacking集成学习算法方法

Stacking是一种集成学习(ensemble learning)的机器学习方法,最早由Wolpert[34]于1992年提出。该方法通常采用两层结构,如图1所示。首先,在第1层利用原始数据集训练多个基学习器,得到多个预测结果;然后将第1层的预测结果作为输入,训练第2层的元学习器,以获得最终的预测结果。这种层级结构有助于提高模型的准确度,并降低泛化误差。

基于Stacking集成学习算法的混凝土强度预测流程,即单个初级学习器5倍交叉验证过程如图2所示。

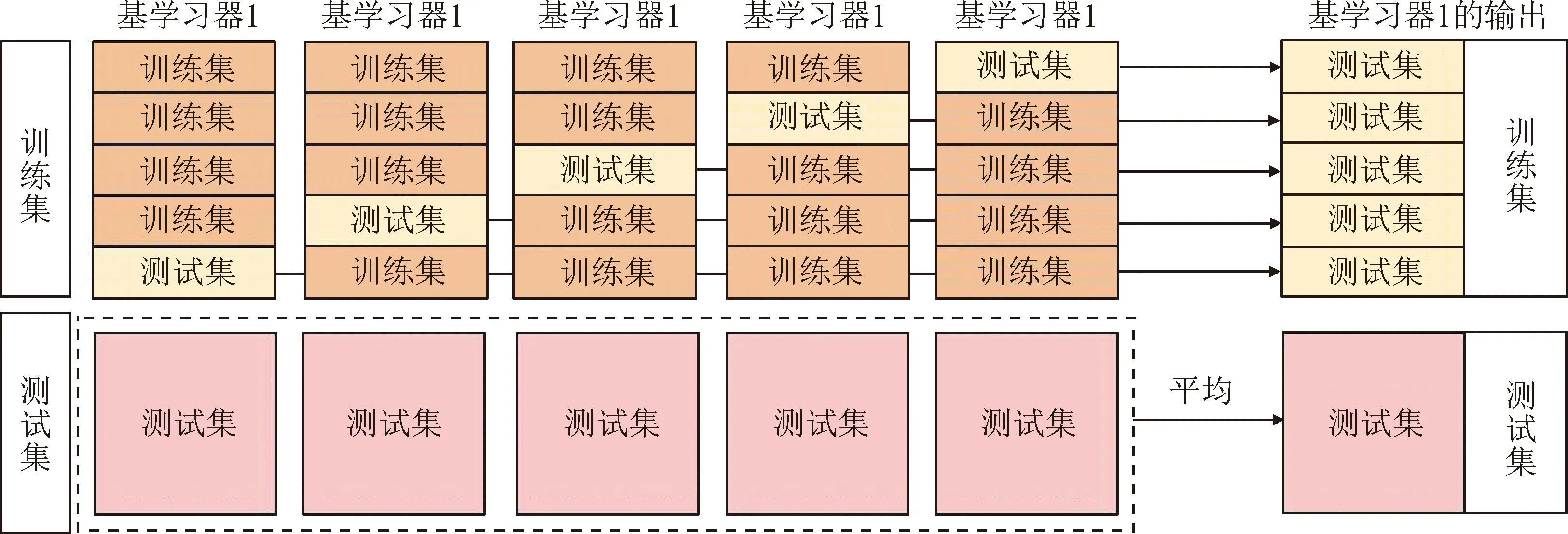
图2 单个初级学习器5倍交叉验证过程Fig.2 5-fold cross validation process for a single beginner learner

1)划分训练集。根据交叉验证的思想,把训练集随机划分为5个相同数量且互不重叠的子数据集。

2)训练基学习器。首先,对于基学习器1,在训练集中随机选择4个子数据集作为训练集,剩余子数据集作为测试集,根据5倍交叉验证的思想,基学习器1得到的输出如图2所示,在原始数据测试集上得到的5个测试结果取平均,最终得到第1个基模型对训练数据的一个Stacking转换。其他基学习器重复上述步骤,可以完成第1层模型训练。

3)训练元学习器。通过利用第1层基学习器产生的混凝土强度预测值构建新的训练集,用于训练第二层预测模型,从而获得最终的混凝土强度预测值。

1.2 Stacking基学习器

在Stacking中,学习能力越强且关联程度越低的基学习器,其模型融合的预测效果就越好。本研究选择XGBoost、CatBoost、MLP、RF基学习器作为Stacking集成模型第1层预测算法。在第2层预测模型中,为了避免过拟合,选择结构简单且泛化能力强的线性回归(linear regression, LR)算法作为元学习器。

1.2.1 XGBoost

XGBoost是由Chen等[35]在2016年提出的一种基于决策树的集成学习算法,采用了GB的思想,通过不断地添加基学习器,每次训练一个新的决策树,从而尽可能地纠正之前模型的误差。具体来说,每次训练新的决策树时,XGBoost会根据之前模型的残差来更新样本权重,并根据新的样本权重训练出一个新的决策树。XGBoost在传统梯度提升算法的基础上,通过引入正则化和树剪枝等技术,可以有效避免过拟合现象,并提高模型的泛化能力。

1.2.2 CatBoost

CatBoost是由Prokhorenkova等[36]于2017年首次提出的一种基于梯度提升决策树的算法框架。CatBoost在每一步决策树运算过程中,根据上一个决策树的残差调整权重,确保本次计算沿着上一次计算的最小残差方向进行。这一策略有效地减少了条件偏移和梯度偏差的影响,从而使得该算法能够实现高精度预测,并具备较强的泛化能力。

1.2.3 Random forest

随机森林是一种基于装袋的集成学习算法,最早由Breiman[37]在2001年提出。在RF中,首先通过采用自助抽样方法对原始数据进行有放回采样,生成多个样本;然后再为每个bootstrap样本构建分类树,将分类树的预测组合在一起后通过投票方式组合在一起,得到最终的预测结果。该模型能够有效处理高维度的数据,且无需进行特征选择,具有优良的泛化能力、快速的收敛速度以及较少的调节参数等优点。

1.2.4 MLP

多层感知器(multilayer perceptron, MLP)是一种常见的前馈神经网络模型[38]。它由多个神经元组成,每个神经元分为输入层、隐含层和输出层。输入层中包含一个权值矩阵,用来描述输入与输出数据之间的关联;隐含层根据权值矩阵的设置确定网络结构及隐层节点数;输出层中采用MLP神经算法实现运算,最终得到预测结果,对非线性问题有很好的表现能力和泛化能力。

1.2.5 SHAP 值算法

SHAP 算法基于 SHAP值进行模型可解释性,这一概念来自博弈论[39],其核心思想是利用加性模型G(x)来逼近已训练好的分类器F(x),具体如式(1)所示。

(1)

式中:φ0为模型对任一样本预测结果的期望,即所有样本标签的均值;φj是n维样本x的第j个特征的SHAP值。

每个样本x的任一特征xj在不同特征子集中的边际贡献的均值,即定义为该特征的 SHAP 值φj,具体计算方式如式(2)所示。

(2)

式中: {x1,x2,……,xn}为全体输入特征的集合,S为不包含特征xj的特征子集。

2 数据预处理、模型构建和评估

2.1 数据描述

数据集的数量、质量和多样性对于模型的预测能力和泛化能力具有至关重要的作用。本研究采用YEH[40]收集到的1 030组混凝土数据,均属于高性能混凝土(high-performance concrete, HPC),数据集涵盖了1 030×9组数据,其中前7组数据表示每立方混凝土水泥、高炉矿渣粉、粉煤灰、水、减水剂、粗骨料和细骨料的用量,第8组表示混凝土养护时间,第9组表示混凝土抗压强度。每组数据的名称、总数、最大值、最小值、平均值和标准差等信息如表1所示,为了更全面了解数据的分布情况,绘制了每组数据的统计分布直方图,如图3所示。

表1 1 030组数据集的描述性统计Table 1 Descriptive statistics of 1 030 group dataset

图3 数据的统计分布直方图Fig.3 Statistical distribution histogram of data

2.2 数据预处理

2.2.1 异常值处理

模型构建过程中的极端异常值严重影响模型的预测效果。根据表1可以看出,对于龄期特征,其值在1～365 d,其中75%在56 d及以内,结合图3可知龄期数据集属于右偏态分布。为提供可靠且高质量的数据,本研究对初始样本中的部分异常值和离群点进行处理,以3倍标准差为阈值,剔除绝对值大于该阈值的数据,最后剩余981组数据。剔除异常值后各组的数据如表2所示。

表2 剔除异常值后各组的数据Table 2 Data of each group after eliminating outliers

2.2.2 归一化处理

为消除各输入参数间量纲对结果带来的影响,本研究对数据集进行了归一化处理,通过缩放将每一个特征的取值范围归一化到[0, 1],对于所有输入特征采用式(3)进行计算。

(3)

式中:xmin为某一个特征的最小值,xmax为对应特征的最大值。

2.3 模型构建和评估

数据集分为训练集和测试集,训练集是用来训练模型,而测试集来评估建立模型的性能。本研究中,训练集和测试集分别按照70%和30%进行划分。

采用均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)和决定系数(R-square,R2)作为预测指标。其中,RMSE和MAE衡量预测结果的全局和局部绝对误差,两者的值越小表示模型的预测精度越高;R2衡量预测整体效果,其值越大表示模型的拟合效果越好,具体计算如式(4)～(6)所示。

(4)

(5)

(6)

3 结果与讨论

3.1 基学习器超参数选择及预测结果

为保证Stacking模型性能趋于最优,需要对各基学习器的学习能力与模型组合对比进行分析。首先,使用经过预处理的数据集训练各基学习器,然后使用基于概率模型的贝叶斯优化确定各模型的最优超参数组合。各单算法模型的超参数及预测误差如表3所示。由表3可知:从决定系数R2来看,XGBoost在测试集上的拟合效果最好,Catboost次之,RF排第三,MLP最差;结合计算得到的RMSE值,XGBoost的训练误差为3.807,均小于Catboost、MLP和RF的训练误差(分别为4.006,9.492和5.007);另外,MAE也说明了XGBoost具有较好的预测精度。各基学习器的预测结果如图4所示,图中横坐标为高性能混凝土强度(HPCCS)的试验数据,纵坐标为各基学习器计算得到的强度值,红色实线为等值线(表示试验值和模型值相等的情况),数据点越靠近实线表明模型的拟合优度越好,结果表明,XGBoost与Catboost具有较好的预测精度,这是因为XGBoost对损失函数进行了二阶泰勒展开,优化过程使用了一阶和二阶导数信息进行更新迭代,使得模型训练更充分;Catboost是基于梯度提升决策树的算法框架,可以有效避免条件偏移和梯度偏差,预测性能也较优。

表3 基学习器超参数组合及预测误差Table 3 Base learner hyperparameter combinations and prediction errors

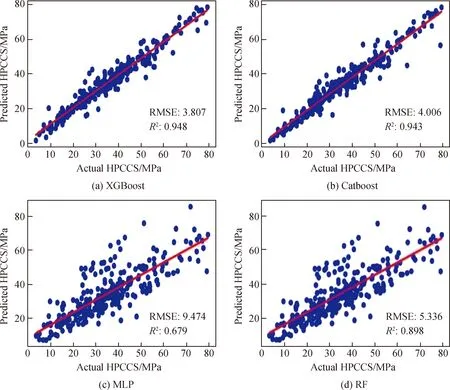
图4 各基学习器的预测结果Fig.4 Prediction results of each base learner

在测试集上,以混凝土预测值和实际值之间的差值作为误差。图5为各基学习器的误差直方图,图中横坐标为基学习器预测的误差值,纵坐标为误差值对应的频率,从图5中可以看出,XGBoost和Catboost模型大约80%的预测值误差小于5 MPa,再次说明了XGBoost对高性能混凝土强度具有较高的预测精度。

3.2 Stacking集成模型预测性能分析

由于XGBoost和Catboost都属于Boosting的一种集成学习方法,均采用梯度提升树算法作为基础模型。因此,考虑到基学习器的差异性,本研究选择XGBoost和Catboost分别与MLP、RF进行融合作为Stacking模型的基学习器。不同基学习器组合的Stacking集成模型预测结果如表4和图6所示。其中,图6(a)、(c)、(e)、(g)横坐标为高性能混凝土强度的试验数据,纵坐标为各Stacking模型计算得到的强度值, 图6(b)、(d)、(f)、(h)横坐标为数据集数量,纵坐标为各Stacking模型预测值与试验值的偏差值。

表4 基学习器组合的stacking集成模型预测结果Table 4 Prediction results of stacking ensemble model with combination of base learners

预测结果显示,综合R2、RMSE、MAE三个方面,基学习器组合XGBoost和RF相对于其他组合方式建立的Stacking集成学习模型具有更高预测精度和更稳定的预测结果,模型预测指标R2、RMSE、MAE的值分别为0.949、3.776、2.605。集成Catboost、MLP与RF和集成XGBoost与RF模型的结果优于每个基学习器,这表明Stacking模型中元学习器纠正了基学习器预测错误的样本,并融合多个基学习器的优点,从而提高了模型的预测精度;而集成XGBoost、MLP与RF和Catboost与RF模型的预测结果分别低于基学习器XGBoost和Catboost的结果,说明集成学习需要合理地选择基学习器,并针对具体问题进行调整和优化,如果组合不当,可能出现集成模型表现不如单个基学习器的情况。

4 模型的验证和可解释分析

4.1 模型的验证

为了验证基于XGBoost和RF模型融合的Stacking集成学习模型的泛化性能,本研究从Yeh[41]中收集103组高性能混凝土数据开展验证工作,数据集包括水泥、水、粗骨料、细骨料、减水剂、矿渣、粉煤灰,以及龄期(28 d)和抗压强度。试验值与模型值的验证结果如图7所示。在图7中,横坐标为高性能混凝土强度的试验数据,纵坐标为Stacking集成学习模型计算得到的强度值,红色实线为等值线(表示试验值和模型值相等的情况),数据点越靠近实线表明模型的拟合优度越好。由图7可知,试验值和模型值之间的关系非常接近,决定系数R2=0.947,均方根误差RMSE=3.840,说明本研究建立的基于XGBoost+RF模型融合的Stacking集成学习模型能较好地反映各因素与混凝土强度之间的关系,具有较高的预测精度和良好的泛化性能。

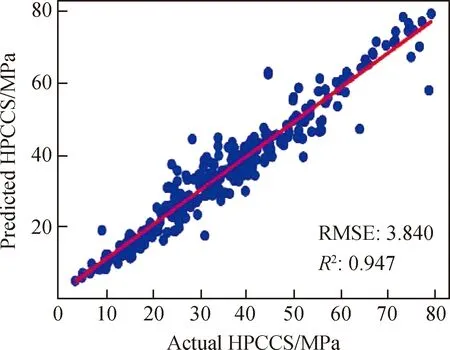
图7 验证模型预测结果Fig.7 Prediction result of validate the model

4.2 可解释分析

本文研究了配合比参数对高性能混凝土强度的影响,并采用基于SHAP值进行模型可解释分析。本节对整体表现较好的基学习器XGBoost模型进行输入变量的特征重要性分析。

SHAP值是一种定量化的模型可解释性工具,有以下两点规律:一是特征对总体模型的重要性,即某一特征的总SHAP值越大,该特征对于模型的重要度越高;二是特征对预测标签的重要性,即就某一特征对应各分类标签而言,SHAP值越大,说明该特征对该标签的预测越重要,同时也使得该标签更容易被正确预测。各项特征的重要性分析如图8和图9所示,从图中可以看出,最重要的输入特征变量是龄期和水泥,而相对次要的输入特征参数是水含量、细骨料和减水剂。在两个最重要的输入特征变量中,龄期对高性能混凝土的抗压强度具有最重要的影响。这是因为随着龄期的增加,水泥继续水化,从而提高高性能混凝土的抗压强度。水泥是影响抗压强度的另一个重要因素,因为水泥通过胶结将混凝土构件黏结在一起,黏结力越大,高性能混凝土的抗压强度越强。