振捣作用下新拌混凝土流变性和气泡结构研究

金 阳,潘俊铮,仲 亮,韩咏书,周光照,高小建

(1.中国建筑第七工程局有限公司,郑州 450004;2.哈尔滨工业大学土木工程学院,哈尔滨 150090)

0 引 言

(1)

Herschel-Bulkley模型是描述非牛顿流体中出现剪切稀化和剪切稠化最常用的流变模型[6],如式(2)所示。

(2)

式中:m表示黏度系数,n表示剪切指数。

Tattersall等[4]发明两点测试法,标志着流变学原理正式应用于混凝土材料。自20世纪70年代以来,旋转流变仪逐渐发展为水泥基材料流变性测试的主要工具,包括平行板类、同轴圆筒类和叶片类等流变仪,如BTRHEOM、BML和ICA流变仪等[7]。然而,新拌混凝土的流变性在受振状态下与静态下不同,且在不同的振动形式下也存在差异[8]。国内外许多学者采用旋转流变仪将样品容器固定在振动台上的方式测量了表面振动下新拌砂浆或混凝土的流变性[9-12],但在振捣作用下,旋转流变仪并不适用。

基于斯托克斯定律的落球法是最基本的液体黏度测量方法[13]。由于水泥基材料不透明,无法直接观测球体的沉降速度,因此目前已有相关研究的难点为如何改进测试方法获得球体的沉降速度。Petrou等[14]利用同位素标记法追踪了振捣作用下新拌砂浆中不同密度的球体的沉降过程;Koch等[15]采用玻璃微珠和硅油制成与砂浆流变性相近的透明流体,研究了振捣作用下流变性、气泡和球体颗粒的运动规律;Pichler等[16]改进了斯托克斯型黏度计,研究了振捣作用下新拌砂浆近振源处的幂律流体特性。此外,Li等[8]和Banfill等[17]通过沿径向等距布置的加速度传感器获得振捣波传播信息,预测了振捣作用半径范围。然而,上述研究中所包括的振捣作用下流变性测试方法仍存在精确度不足、试验环境要求苛刻以及测试过程烦琐等问题。

本文自主开发了基于斯托克斯定律、适用于振捣作用下新拌混凝土流变性的测试和评价方法——拉球法。拉球法是将球体从待测浆体中匀速拉出,并实时监测在不同速率下球体拉出过程中所受到的黏性阻力,再根据所测黏性阻力与拉出速率的关系计算浆体的流变参数。与落球法不同的是,拉球法使球体颗粒始终保持力平衡状态,将需要监测的物理量由沉降速度转化为黏性阻力,更直接且精确。本文还采用气孔分析仪(air void analyzer, AVA)测试新拌混凝土的气泡结构,研究了振捣对新拌混凝土流变性和气泡结构的影响规律。

1 实 验

1.1 原材料与配合比

胶凝材料包括P·O 42.5普通硅酸盐水泥、硅灰和高钙粉煤灰,其主要化学组成和物理性能分别如表1和表2所示。细骨料为天然河砂,细度模数为2.7,粗骨料为碎石,骨料的颗粒级配如表3所示。减水剂为聚羧酸类高效减水剂(superplasticizer, SP),固含量约为40%,减水率为35%。引气剂(air-entrained agent, AEA)的主要成分为天然三萜皂苷。

表1 胶凝材料的主要化学组成Table 1 Main chemical composition of cementitious materials

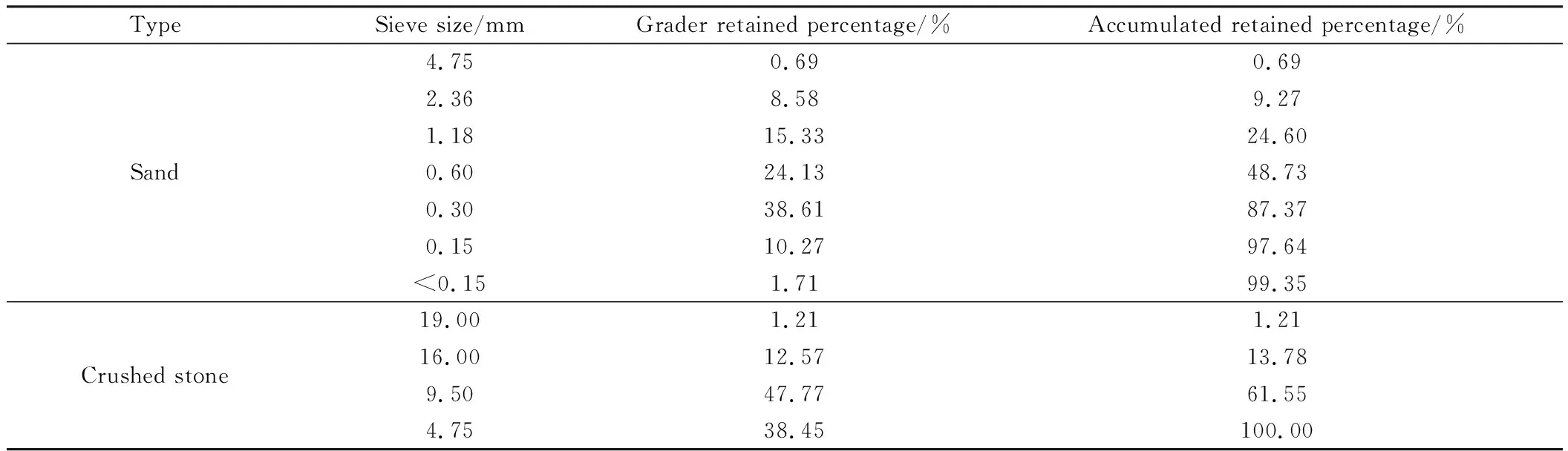
表3 骨料的颗粒级配Table 3 Particle size grading of aggregates

试验分为静置试验(编号为S)和振动试验(编号为D),配合比如表4所示。设计静置试验的目的是分析拉球法与流变仪所测流变参数的相关性,论证拉球法的可靠性。静置试验中掺加硅灰或粉煤灰的目的是增加原材料体系,扩大流变参数变化范围。静置试验砂浆胶砂质量比固定为1∶2。振动试验混凝土设计强度等级为C40,各原材料质量比为m(水泥)∶m(砂)∶m(碎石)∶m(水)=1∶1.25∶2.77∶0.4,减水剂掺量为0.3%(质量分数)。试验环境温度始终保持在(20±2) ℃。

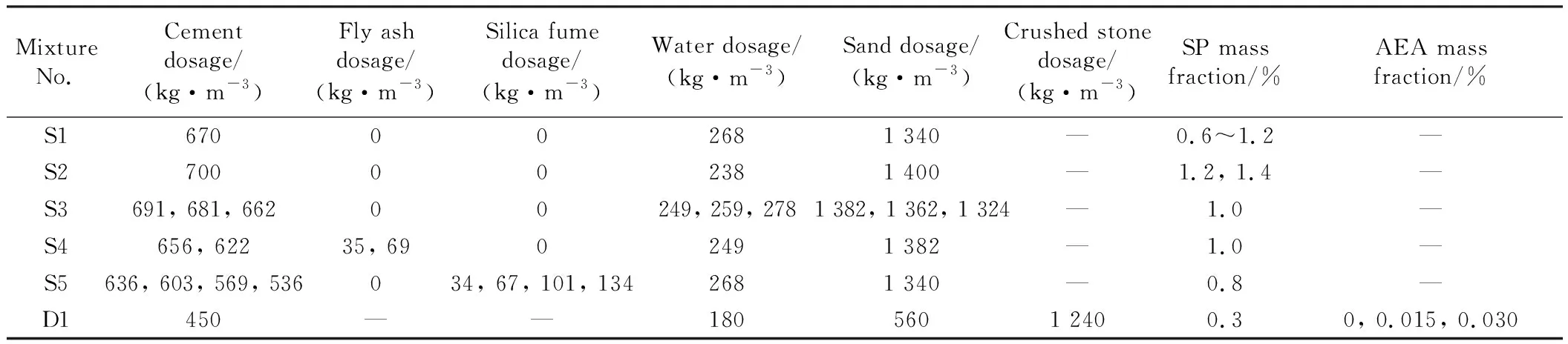
表4 静置试验和振动试验的砂浆和混凝土配合比Table 4 Mix proportion of mortar and concrete in static experiments and vibration experiments

1.2 测试原理

对落球法和拉球法中的球体颗粒进行受力分析,分别如图1(a)和(b)所示。在图1(a)中,球体颗粒以最终恒定速度Vs沉降时,重力M与浮力Fb的合力等于黏性阻力Fs;在图1(b)中,球体颗粒通过细线以恒定速度V拉出时,黏性阻力Fs可以由式(3)进行计算。

图1 刚性球体在新拌砂浆中运动的受力分析Fig.1 Force analysis of a solid sphere particle motion in fresh cement mortar

Fs=Fe-(M-Fb)

(3)

式中:Fe表示作用在细线上的拉力,N。

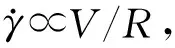
对于Bingham流体而言,由于屈服应力的存在,球体颗粒在沉降过程中周围的流体并非全部为液相,存在具有固体性质的未屈服区。Beris等[19]、Wünsch[20]引入了斯托克斯阻力系数(Stokes drag coefficient,Cs),如式(4)所示。

(4)

式中:F表示作用于球体颗粒沉降外力之和。

无量纲的宾汉姆数(Bingham number,Bn)描述了屈服应力和塑性黏度的相对关系,如式(5)所示。

(5)

根据式(4),Bingham流体的黏性阻力Fs=6πRμpVsCs。Blackery等[22]、Pichler等[16]将Cs表示成Bn的函数形式:

Cs=Cs,N+a(Bn)b

(6)

式中:Cs,N表示牛顿流体的斯托克斯阻力系数,a和b均为常数。

球体在充满Bingham流体的管状容器中发生沉降运动时,Cs,N、a和b的取值均和容器半径Rc与球体颗粒半径R的比值(Rc/R)有关,如图2和表5所示[22]。将式(5)和(6)代入式(4)中可得

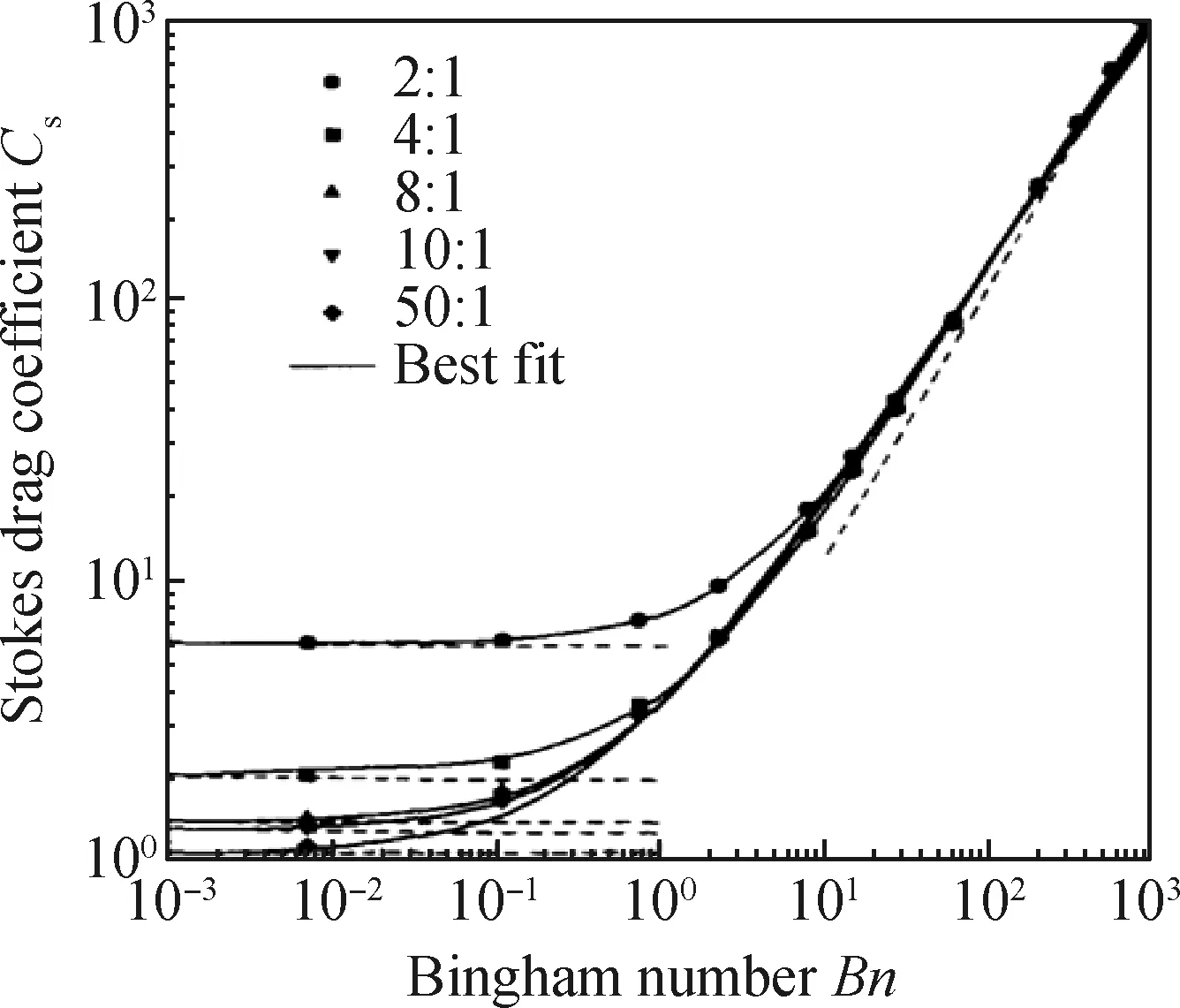
图2 斯托克斯阻力系数Cs与宾汉姆数Bn的关系[22]Fig.2 Correlation between Stokes drag coefficient Cs and Bingham number Bn[22]

表5 从Bingham流体斯托克斯阻力系数的最佳拟合结果中得到的常数(0≤Bn<1 000)[22]Table 5 Constants obtained from best fit of Stokes drag coefficient results for Bingham fluids (0≤Bn<1 000)[22]

(7)

综上所述,采用拉球法测定Bingham流体的流变参数时,已知钢球的密度ρs和半径R,待测浆体的密度ρf,采用确定的管状容器与球体颗粒(Rc/R确定),根据表5中的拟合结果得到相应的常系数Cs,N、a和b,通过测定以不同恒定速度V拉出球体颗粒的绳端拉力Fe,根据式(3)计算得到钢球所受到的黏性阻力Fs。利用数组(V,Fs)绘制Fs/R2-V/R的流变曲线,最后根据式(7)拟合得到流变参数τ0和μp。

1.3 试验方法

拉球法试验装置如图3所示。静置试验所使用的模具为圆柱筒,测试时仅启用单个滑轮,不使用插入式振捣棒;振捣试验所使用的模具为长方体容器,测试时同时启用4个滑轮,且在模具一端使用插入式振捣棒。试验步骤如下:

①开启电源,初始时使钢球在空气中自然静止,对所测力值清零;

②将待测的新拌混凝土砂浆组分均匀地装入长500 mm、宽120 mm、高500 mm的长方体容器(静置试验容器为内径80 mm、高400 mm的圆柱筒),将直径为20 mm的钢球垂直落入其中,调整移动底座位置使钢球始终处于容器的中轴线上,制动移动底座固定位置,待细线在铅锤方向且钢球稳定后,此时所测得的力值为F1;

③调节控制箱上的变速器至初始转速挡位;

④开启插入式振捣棒(仅振捣试验),同时按下上升按钮,使钢球匀速上升,此时所测得的力值为F2;

⑤当将钢球拉出新拌混凝土上表面后立即停止振捣(仅振捣试验)并按下暂停按钮,计算机记录和保存整个拉出过程中拉力传感器所测力值变化;

⑥按下下降按钮,使钢球下降至初始位置,调节控制箱变速器至下一个转速挡位;

⑦重复步骤④至步骤⑥,直到完成所有设置的转速挡位测试;

⑧同一转速下,黏性阻力Fs=(F2-F1)/2,再根据1.2节内容进行计算。

为验证拉球法测量流变参数的准确性,采用法国恺德仪器生产的RheoCAD流变仪对相同配合比的新拌砂浆进行流变参数测定。采用AVA-3000分别测量与振源距离100、400 mm处的新拌砂浆气泡结构。

2 结果与讨论

2.1 拉球法与流变仪所测流变参数相关性

S1与S2组的变量为减水剂掺量。其中S1组水胶比为0.40,减水剂掺量分别为0.6%、0.8%、1.0%和1.2%;S2组水胶比为0.34,减水剂掺量分别为1.2%和1.4%。拉球法和流变仪所测流变曲线如图4所示。由图4可知:在相同水胶比的情况下,随着减水剂掺量的增大,流变曲线斜率变化不明显,表明减水剂掺量对浆体的塑性黏度影响较小;截距在S1-0.6%SP组和S1-0.8%SP组之间大幅减小,表明当减水剂掺量在0.6%～0.8%的范围内增加时,浆体的屈服应力会迅速降低。对比水胶比不同的S1组和S2组,流变曲线斜率有较大变化,低水胶比的浆体塑性黏度更高。

S3组的变量为水胶比,水胶比分别为0.36、0.38、0.40和0.42,减水剂掺量固定为1.0%。拉球法和流变仪所测流变曲线如图5所示。由图5可知:在减水剂掺量不变条件下,水胶比增大使浆体的塑性黏度和屈服应力降低;当水胶比大于0.4时,浆体的塑性黏度较低,屈服应力趋近于零,继续增大水胶比影响不再显著。

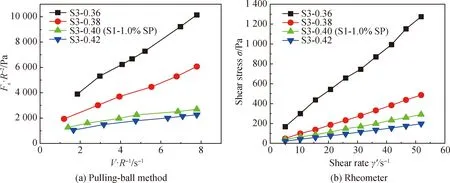
图5 不同水胶比下砂浆的流变曲线Fig.5 Rheological curves of mortar with different water-binder ratios

S4组的变量为粉煤灰掺量,粉煤灰掺量分别为0%、5%和10%,水胶比固定为0.36,减水剂掺量固定为1.0%。拉球法和流变仪所测流变曲线如图6所示。由图6可知,在水胶比和减水剂掺量不变条件下,粉煤灰掺量增大使浆体的塑性黏度和屈服应力逐渐降低。

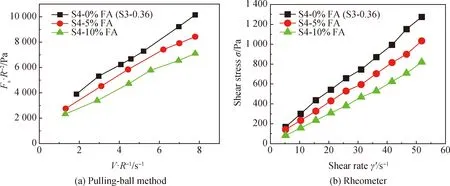
图6 不同粉煤灰掺量下砂浆的流变曲线Fig.6 Rheological curves of mortar with different dosages of fly ash

S5组的变量为硅灰掺量,硅灰掺量分别为0%、5%、10%、15%和20%,水胶比固定为0.40,减水剂掺量固定为0.8%。拉球法和流变仪所测流变曲线如图7所示。由图7可知,在水胶比和减水剂掺量不变条件下,随着硅灰掺量的增大,流变曲线截距逐渐增加,而斜率变化并不明显。这表明硅灰掺量增大使屈服应力增大,对塑性黏度的影响较小。

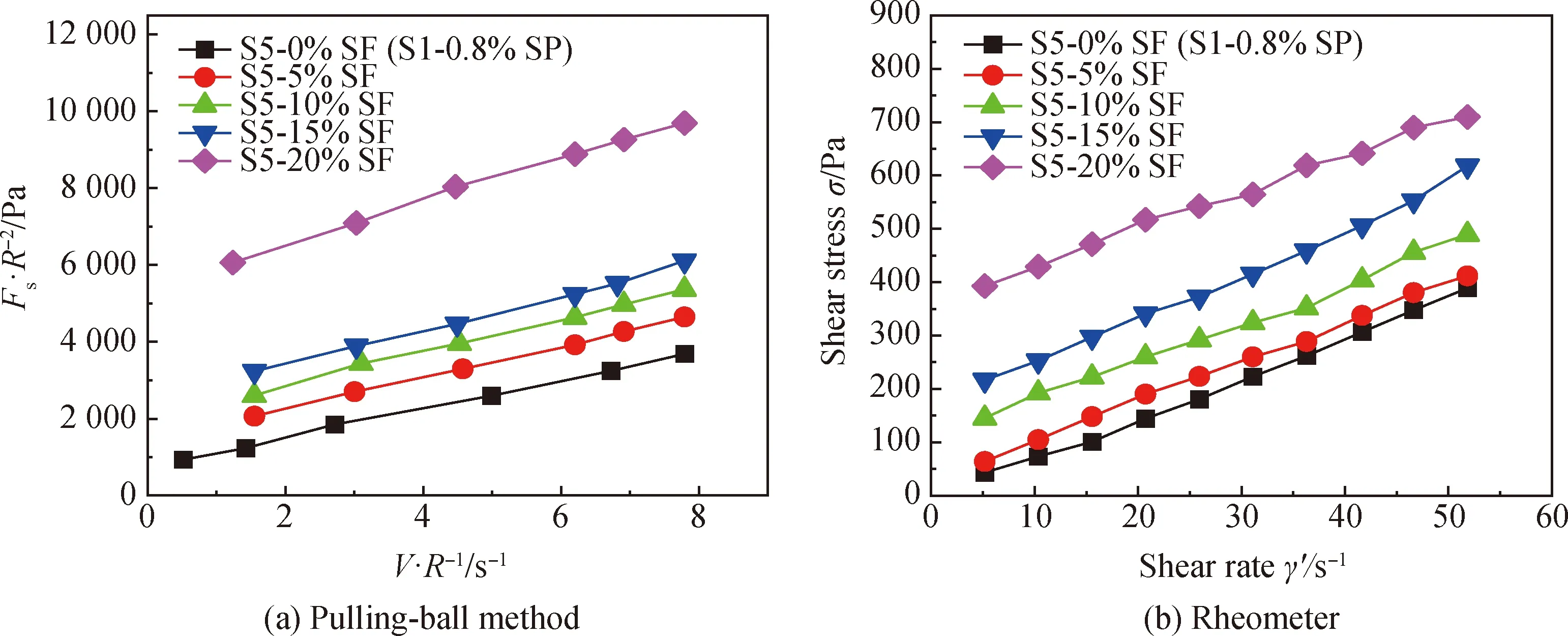
图7 不同硅灰掺量下砂浆的流变曲线Fig.7 Rheological curves of mortar with different dosages of silica fume

从流变学角度出发,水泥、砂浆和混凝土等水泥基材料拌合物通常被视为一种颗粒悬浮液。在不考虑水化作用情况下,固相颗粒经过拌和均匀分散在液相中。颗粒悬浮液存在屈服应力的本质是颗粒间存在摩擦力以及一定的接触角,会阻碍剪切变形;而塑性黏度主要来源于产生剪切变形时流动较慢的液层阻滞较快液层流动的阻力。在上述原材料体系变化中,增大减水剂掺量或水胶比会使固相颗粒之间的摩擦力显著降低,因此宏观上拌合物的屈服应力和塑性黏度显著降低。掺入矿物掺合料主要影响了胶凝材料浆体的流变行为。已有研究表明,粉煤灰微珠效应对浆体流变性能的改善作用显著,能够有效降低胶凝材料浆体的屈服应力和塑性黏度,减少水的吸附量[23]。硅灰颗粒的比表面积较大,表面润湿需水量多,且会吸附一定量的减水剂,降低减水剂整体的分散效果,宏观上表现为屈服应力随硅灰掺量增大而增大[24]。

对上述各试验组的流变曲线进行拟合。其中,通过拉球法所得流变曲线根据式(7)进行非线性拟合,通过流变仪所得流变曲线根据式(1)进行线性拟合。最终通过拟合获得的屈服应力和塑性黏度汇总如表6所示。分别对表6中的塑性黏度和屈服应力进行相关性分析,绘制μp,2-μp,1和τ0,2-τ0,1曲线,如图8所示。

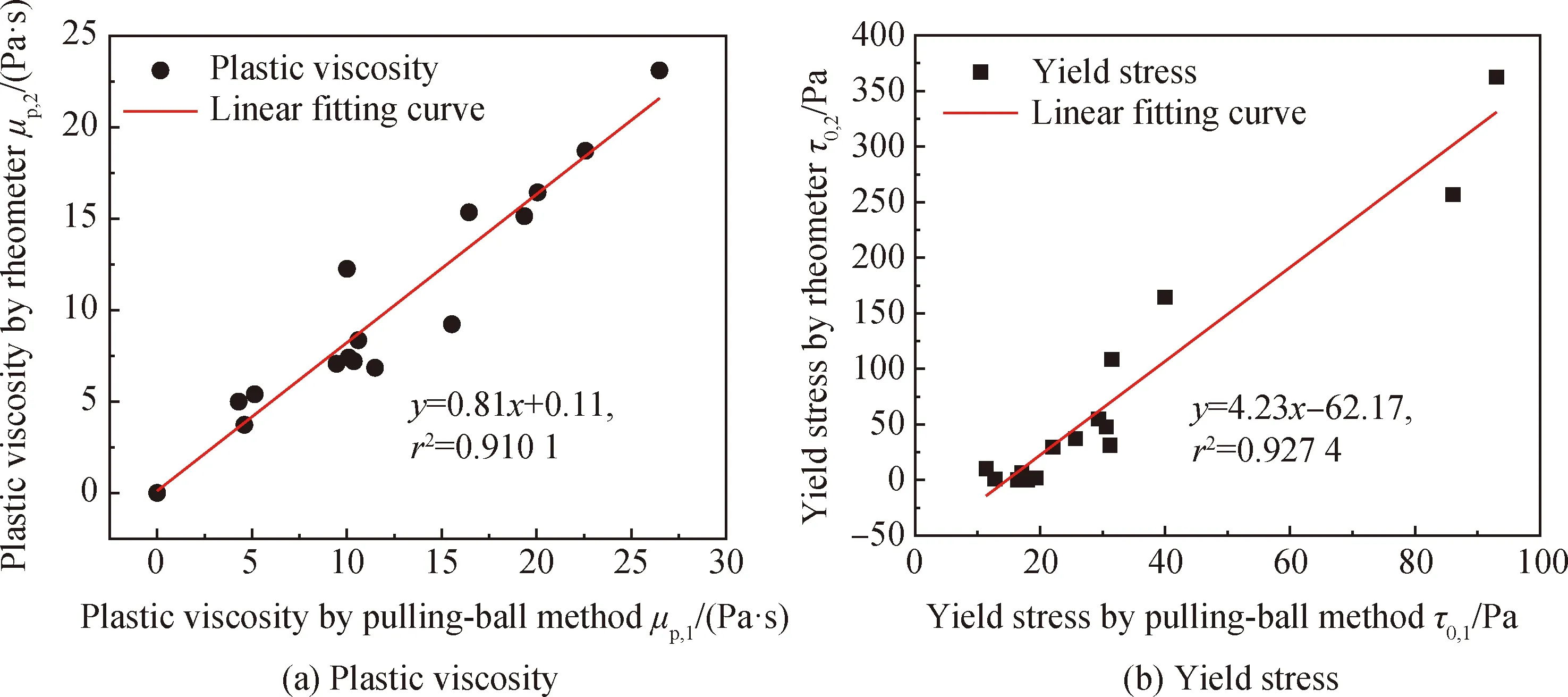
图8 拉球法与流变仪所得流变参数的相关性Fig.8 Correlations between rheological parameters obtained by pulling-ball method and rheometer

表6 砂浆流动度与流变参数Table 6 Slump flow and rheological parameters of mortar

由图8(a)可知,拉球法与流变仪所得塑性黏度之间满足关系:μp,2=0.81μp,1+0.11,相关系数为0.910 1;由图8(b)可知,拉球法与流变仪所得屈服应力之间满足关系:τ0,2=4.23τ0,1-62.17,相关系数为0.927 4。结果表明,拉球法与流变仪所得塑性黏度和屈服应力存在良好的线性相关性,利用拉球法测试新拌混凝土流变性具有可靠性。需要说明的是,屈服应力的拟合方程存在τ0,2<0的可能。出现该情况与拉球法流变曲线采用非线性拟合有关。如表6中的S3-2和S3-3组,流变仪所得屈服应力趋近于零,而拉球法所得屈服应力τ0,1范围为12.7～18.0 Pa,存在通过计算所得τ0,2<0的情况。当出现该情况且τ0,2的计算值接近于零时,则表明待测浆体的屈服应力极低。两种方法所得屈服应力的线性关系系数为4.23,出现该情况可能有以下原因:1)待测浆体的屈服应力过低,通过流变曲线Bingham拟合所得屈服应力存在误差;2)拉球法在高速拉出时匀速阶段过短,造成所测平均黏性阻力出现误差;3)平均黏性阻力在计算时忽略了滑轮的转动惯量,以及在理想化过程中产生的其他误差。

2.2 静态下新拌混凝土流变性与气泡结构

静态下D1试验组流变曲线、含气量和气泡间距系数如图9所示,AVA所得气泡结构如图10所示。其中,AVA测试将样品保存在5 ℃环境中是为了尽可能减少浆体在上一组测试过程中的气泡结构变化。结果表明,AEA对新拌砂浆的塑性黏度影响较小,而屈服应力随AEA掺量的增大而降低。

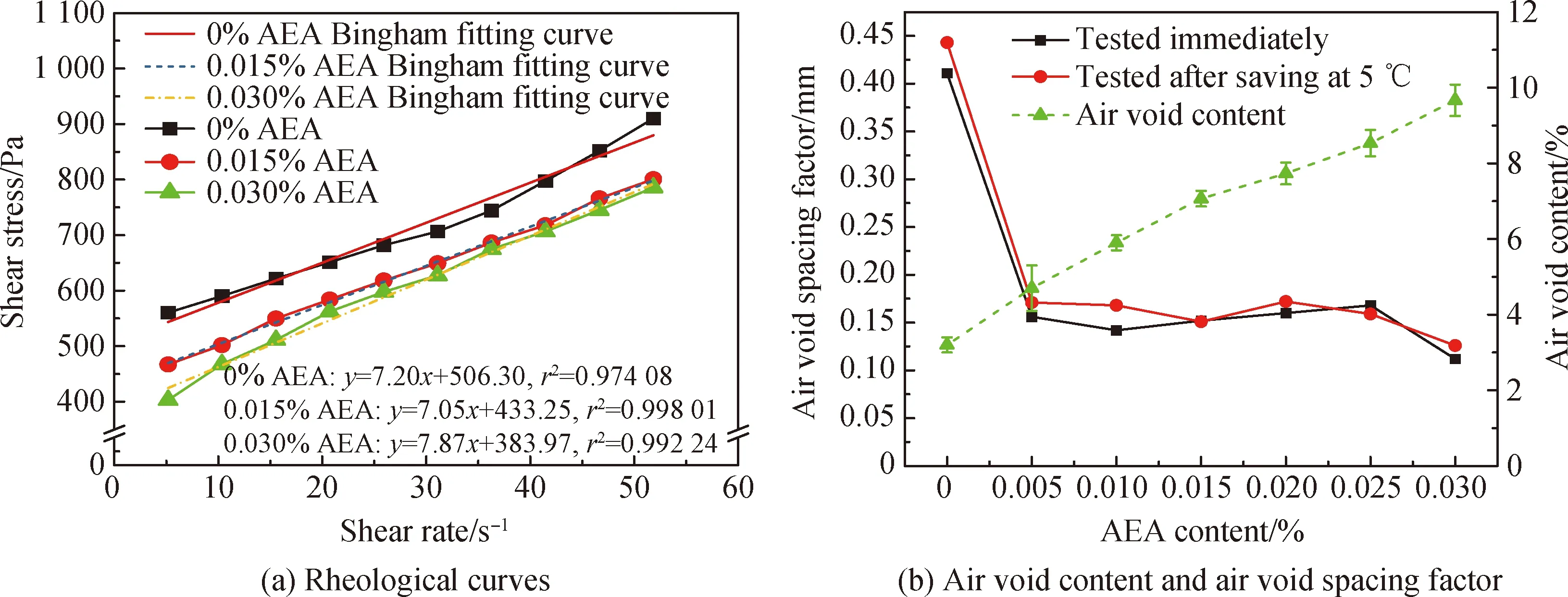
图9 不同AEA掺量下新拌砂浆流变曲线、含气量与气泡间距系数Fig.9 Rheological curves, air void content and air void spacing factor of fresh mortar with different dosages of AEA

已有研究[25-26]表明,随着AEA掺量的提高,新拌砂浆塑性黏度增大,屈服应力先增大后减小。而Struble等[27]发现,在不含减水剂的水泥浆体中,随着含气量增大,新拌浆体的屈服应力增大而塑性黏度降低。Zhang等[28]和Chia等[29]持不同观点,引气混凝土的屈服应力和塑性黏度低于非引气新拌混凝土,含气量增大会使塑性黏度降低而屈服应力基本保持不变。上述研究表明,AEA引入微小气泡对新拌浆体流变性的影响较为复杂。一方面,微小气泡对水泥颗粒产生吸附-桥接作用,形成“气泡桥”,增大新拌浆体的屈服应力;另一方面,在拌合物流动过程中气泡可以产生变形从而降低新拌浆体整体的塑性黏度[27]。

2.3 振捣作用下新拌混凝土流变性与气孔结构

在振捣试验中,不同AEA掺量下钢球所受平均黏性阻力随振源距离变化如图11所示。结果表明:振捣会极大幅度降低近振源处(与振源距离小于200 mm)的黏性阻力,且不同AEA掺量下,近振源处的黏性阻力降低程度相近;当与振源距离大于200 mm后,黏性阻力随与振源距离的增加而增大。当未掺入AEA时,振捣使近振源处黏性阻力分别降低了93.9%和93.7%,使远振源处(与振源距离大于300 mm)黏性阻力分别降低了55.0%和49.0%;当AEA掺量为0.015%时,振捣使近振源处黏性阻力分别降低了92.5%和93.7%,使远振源处黏性阻力分别降低了54.5%和50.6%;当AEA掺量为0.030%时,振捣使近振源处黏性阻力分别降低了92.0%和91.0%,使远振源处黏性阻力分别降低了47.5%和41.9%。因此,随着AEA掺量增加,远振源处黏性阻力降低幅度逐渐减小。

经压力法含气量测定,当AEA掺量为0%、0.015%和0.030%时,静置试验新拌浆体含气量分别为3.2%、7.1%和9.7%,振捣试验新拌浆体含气量分别为4.6%、7.6%和9.7%。经AVA测定,不同AEA掺量下砂浆组分的气泡孔径分布与累积曲线如图12所示,总含气量与气泡间距系数如表7所示。结果表明,振捣可有效排出新拌砂浆中的较大气泡(孔径大于500 μm)而保留微小气泡(孔径小于200 μm)。振捣对高AEA掺量下新拌砂浆排出较大气泡的作用效果更强。当未掺入AEA时,由于整体含气量较低,振捣作用下浆体气孔结构和气泡间距系数变化较小;相较于静置试验,当AEA掺量为0.015%时,振捣使孔径在[500,1 000) μm的气泡含量降低了31.0%,使孔径在[1 000,2 000) μm 的气泡含量降低了10.3%,含气量变化较小,气泡间距系数降低;当AEA掺量为0.030%时,振捣使孔径在[500,1 000) μm的气泡含量降低了84.8%,使孔径在[1 000,2 000) μm 的气泡含量降低了36.4%,总含气量在近振源和远振源处分别下降了1.5%和0.9%,气泡间距系数无明显变化。

表7 不同AEA掺量下砂浆含气量与气泡间距系数Table 7 Air void content and air void spacing factor of mortar with different dosages of AEA

平均黏性阻力反映了球体颗粒在新拌砂浆中竖直方向运动时受到的阻力大小。上述研究表明,振捣使近振源处浆体的平均黏性阻力降低90%以上。因此适宜的振捣作用使得混凝土近振源处粗骨料沉降、气泡发生融合和逸出,使混凝土达到最密实状态。平均黏性阻力结合气泡结构分析能够客观评价新拌混凝土所受到的振捣影响范围和程度。混凝土在静态下的屈服应力和塑性黏度对振捣作用范围有显著影响,在实际工程中安排合理的振捣时间和振捣间距具有重要意义,有待后续进一步研究。

3 结 论

1)对于不同体系、不同配合比的砂浆,拉球法与流变仪所测得的流变曲线规律一致,且所测得的塑性黏度和屈服应力具有良好的线性相关性,表明拉球法测试新拌混凝土流变性具备可靠性。

2)振捣使距离振源200 mm范围内砂浆组分的黏性阻力降低90%以上。不同AEA掺量下距离振源200 mm范围内黏性阻力的降低幅度相近,且随着AEA掺量增加,远振源处(与振源距离大于300 mm)黏性阻力降低幅度逐渐减小。

3)振捣可有效排出新拌砂浆中的较大气泡(孔径大于500 μm),而保留微小气泡(孔径小于200 μm)。

4)振捣对高AEA掺量下新拌砂浆排出较大气泡的作用效果更强。当未掺入AEA时,振捣对浆体气孔结构和气泡间距系数影响较小;当AEA掺量由0.015%增大至0.030%时,振捣使孔径在[500,1 000) μm的气泡含量降幅由31.0%增大至84.8%,使孔径在[1 000,2 000) μm 的气泡含量降幅由10.3%增大至36.4%。