基于KJHH模型的基坑开挖概率反分析方法
2023-11-30张军波周张见虞梦菲
张军波,费 杰,周张见,汪 轮,虞梦菲
(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;2.浙江华东工程咨询有限公司,浙江 杭州 311122; 3.浙江省岱山经济开发区环城投资集团有限公司,浙江 舟山 316212;4.浙江工业大学 土木工程学院,浙江 杭州 310023)
随着我国现代化城市建设的不断推进,为了缓解土地资源紧缺的问题,最有效和直接的方式是充分利用垂直空间发展高层建筑和地下空间建设。同时,这些工程的基坑深度也在不断加深,为基坑工程的安全施工带来了极大的挑战。在开挖基坑的过程中,会引起周边地表沉降和围护结构侧移。过大的基坑变形,不仅会造成邻近建(构)筑物开裂、地下管线破裂以及周边道路不均匀沉降等结构破坏,还会对人民的生命和财产安全造成极大的破坏。因此,在基坑开挖的过程中需要提前预测基坑变形,关注最大变形,严格把控基坑变形,减少基坑事故的发生。目前基坑开挖变形预测研究,主要采用的是数值分析方法[1]和经验公式法[2-4],其中经验公式因其计算简便,而在工程实际中被广泛应用。如Peck等[2]基于芝加哥和奥斯陆的基坑开挖案例,最早提出预测基坑开挖地表沉降预测的经验模型,建立不同土体类型的地表沉降预测曲线;Kung等[3]基于大量的开挖工程案例和有限元模拟经过回归拟合提出KJHH模型,可以用来预测软黏土基坑开挖最大墙体侧移和地表沉降;Ou等[4]基于台北大量的基坑开挖案例,考虑了开挖深度对墙体最大侧移的影响,建立了台北墙体最大侧向位移和开挖深度的关系曲线。然而,由于土体是一种天然材料,具有各向异性和不规则性,土体参数难以确定[5],经验公式对基坑开挖变形的预测往往和现场观测值存在较大的差异。针对这个问题,通过概率反分析方法,利用观测数据更新土体参数[6-9],提高基坑变形预测的准确性,在一定程度上弥补了经验公式预测结果不准确的缺陷。
笔者提出一种基于KJHH模型,以最大地表沉降和最大墙体侧移为观测信息,采用多重数据同化集合平滑器(ES-MDA)算法对土体参数进行更新的概率反分析方法。以台北TNEC基坑开挖工程为例,通过笔者方法对基坑的最大地表沉降和最大墙体侧移进行预测,并与现场观测值进行对比研究,验证了笔者方法的有效性。
1 基坑开挖的概率反分析方法
根据KJHH模型建立基坑变形和土性参数之间的关系,基于ES-MDA算法融合观测数据,对模型参数进行更新,利用更新后的模型参数,预测基坑开挖的最大墙体侧移和最大地表沉降。对KJHH模型和ES-MDA算法进行介绍。
1.1 KJHH模型

根据KJHH模型,首先计算最大墙体侧移δhm,计算式为
δhm=a0+a1X1+a2X2+a3X3+a4X4+a5X5+a6X1X2+a7X1X3+a8X1X5
(1)
(2)

表1 转换系数
然后计算变形率R(最大地表沉降δvm和最大墙体侧移δhm的比值),计算式为
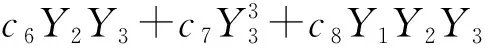
(3)
式中:Y1=∑Hclay/Hwall,其中∑Hclay为墙体深度范围内所有黏土层厚度的总和,Hwall为墙体长度;Y2=su/σ′v;Y3=Ei/1 000σ′v;常系数ci(i=0,1,…,8)由最小二乘法得到,c0=4.556 2,c1=-3.401 51,c2=-7.376 97,c3=-4.994 07,c4=7.141 06,c5=4.600 55,c6=8.748 63,c7=0.380 92,c8=-10.589 58。
最后计算最大地表沉降δvm,计算式为
δvm=Rδhm
(4)
1.2 多重数据同化集合平滑器(ES-MDA)
贝叶斯方法可以利用实时获得的观测值对模型参数进行更新,对于基坑开挖的多阶段观测数据处理一般有两种方式:第一种是依次融合各阶段监测值,更新土体参数,即分步更新。具体而言,利用第i阶段的观测数据对土体参数进行更新,获得土体参数的后验分布,并假设后验分布类型,将其作为第i+1阶段的先验分布进行下一阶段的土体参数更新;第二种是将多阶段的观测值作为整体,一次性使用所有阶段的观测值更新土体参数,即整体更新。具体而言,利用i阶段及之前所有阶段的观测值对土体参数进行更新,利用更新后的土体参数预测后续开挖阶段的基坑开挖变形[11-12]。与分步更新相比,整体更新的集合不假设后验分布类型,减少了更新结果的误差。集合平滑器(ES)算法[13]及其迭代算法(ES-MDA)[14]可以有效实现贝叶斯整体更新,ES-MDA算法的计算步骤如下:
1) 给定迭代次数Na,并针对每次迭代确定对应的膨胀系数αi(i=1,2,…,Na),αi需要满足
(5)
2) 从模型参数的先验分布中随机生成Ne个样本,构成初始样本集合M1=[m1,1,m2,1,…,mNe,1],下标的第1个数字表示样本号,第2个数字表示在集合中的迭代步。
3) 在第i次迭代中,对样本集合Mi=[m1,i,m2,i,…,mNe,i]中的每一个样本通过正向模型进行计算,获得预测值dj,i,计算式为
dj,i=f(mj,i)j=1,2,…,Ne
(6)
4) 利用已有的所有观测值对初始(上一时刻)的样本进行更新,计算式为
mj,i+1=mj,i+CMD(CDD+R)-1(dobsj-dj,i)
(7)
dobsj=dobs+R1/2zd
(8)
式中:CMD为模型参数mi和预测值di的协方差矩阵;CDD为预测值di的自协方差矩阵;R为观测误差的协方差矩阵;dobsj为观测值加入随机扰动后的样本,假设现场观测值是相互独立的,且zd服从高斯分布,zd~N(0,I),I为单位矩阵。
5) 重复步骤(3,4),直到完成Na次迭代。
2 台北TNEC基坑算例分析
2.1 算例介绍
以台北TNEC基坑开挖为例[4,15-16],验证笔者方法预测基坑变形的有效性。该工程的开挖宽度B=41.2 m,挡土墙厚度t=0.9 m,挡土墙长度Hwall=35 m,黏土名义厚度∑Hclay/Hwall=0.87,采用明挖法自上而下进行施工,开挖过程分为7个阶段[17],工程概况、场地所涉及的土层剖面和开挖顺序如图1所示,各阶段的开挖深度、系统刚度如表2所示。
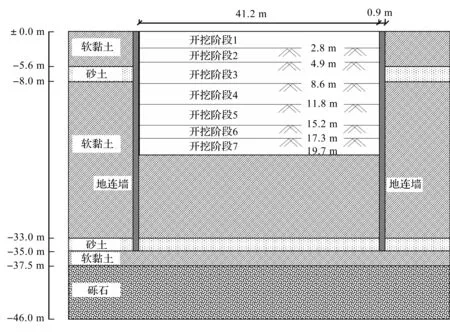
图1 项目概况、土体剖面和开挖顺序示意图Fig.1 Project overview, soil profile and excavation sequence diagram
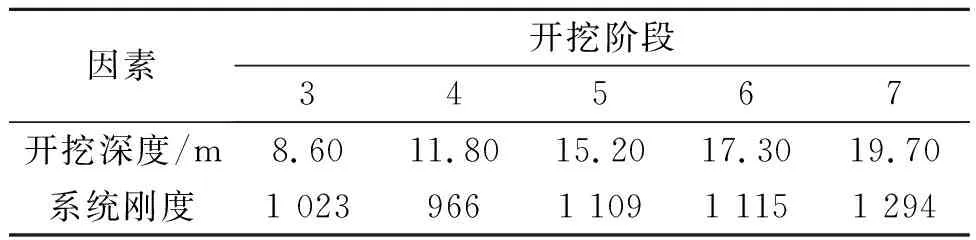
表2 各阶段开挖深度和系统刚度
根据KJHH模型,最大墙体侧移和最大地表沉降受开挖深度影响,前两个开挖阶段的变形模式与后续阶段不同,结合这两个阶段观测值更新土体参数(su/σ′v和Ei/σ′v)的效果欠佳[18],从第3阶段开始进行概率反分析,假设土体参数su/σ′v和Ei/σ′v的先验分布服从对数正态分布,使其转换为正态分布后的均值分别为0.25和500,变异系数为0.16[18]。基于ES-MDA算法,融合各开挖阶段现场观测数据,更新土体参数,并利用更新后的土体参数进行基坑变形预测。具体而言,当第3阶段开挖结束后,利用第3阶段的最大墙体侧移和最大地表沉降观测值通过式(7,8)进行土体参数更新,利用更新后的土体参数预测第3~7阶段的基坑变形;当第4阶段开挖结束后,利用第3,4阶段的最大墙体侧移和最大地表沉降观测值对土体参数进行更新,并预测第4~7阶段的基坑变形;以此类推,获得各阶段的基坑开挖变形预测。
2.2 基坑开挖变形预测结果
在ES-MDA算法中,迭代次数、膨胀系数取值:Na=8,αi=[2 000,1 000,500,42.50,13.68,5,5,2],样本量为500。图2显示了融合不同开挖阶段监测数据的基坑各阶段变形预测。图2中:第3阶段表示融合第3阶段观测值,第4阶段表示融合第3,4阶段观测值,以此类推。由图2可以看出:虽然各阶段预测结果低估了基坑开挖的变形,但是随着融合的不同开挖阶段观测数据的增加,预测的均值逐渐向现场观测值靠拢,预测结果的置信区间逐渐变窄,预测的基坑最大墙体侧移和最大地表沉降的准确性在整体趋势上逐渐提高。
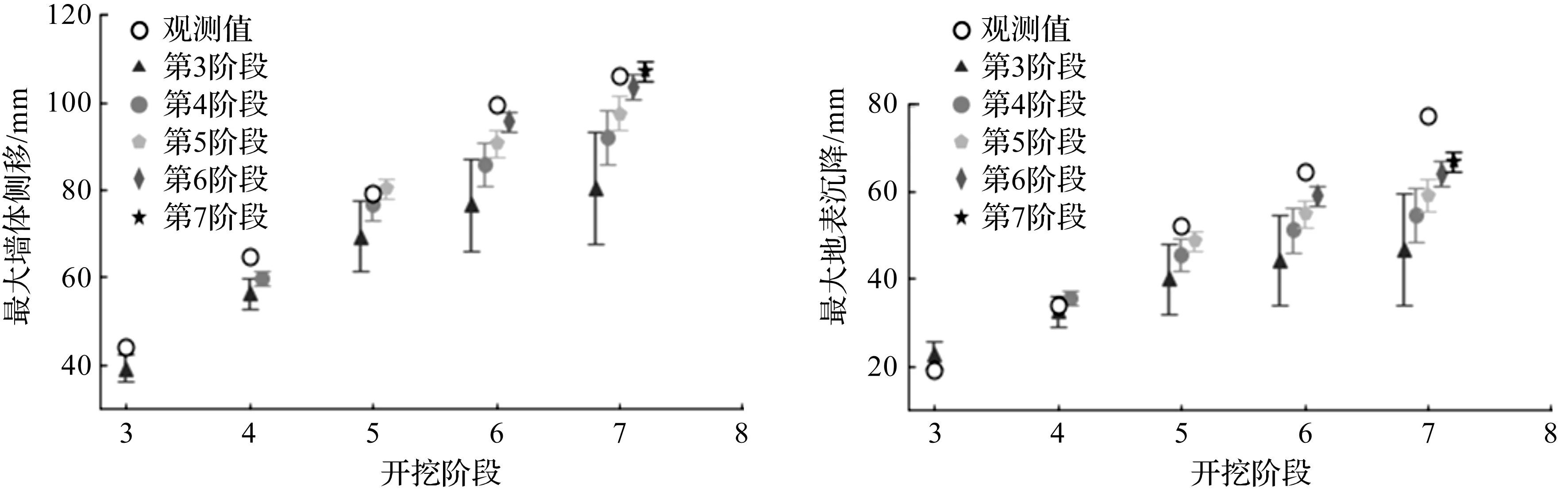
图2 开挖变形预测Fig.2 Excavation deformation prediction
2.3 先验分布类型对预测结果的影响
在概率反分析方法中首先需要假设土体参数的先验分布,先验信息会直接影响土体参数更新及基坑开挖变形预测。为了研究先验分布的统计特征对TNEC工程基坑开挖最大地表沉降和最大墙体侧移的影响,基于土体参数先验分布服从正态分布(先验分布Ⅰ)和均匀分布(先验分布Ⅱ)进行基坑开挖变形响应预测。先验分布Ⅱ的上下限取自小应变三轴试验中17组数据[19]的最大最小值,土体参数先验分布统计特征[18-19]如表3所示。

表3 先验分布
从第3阶段开始,利用监测数据分别对先验分布Ⅰ和先验分布Ⅱ的土体参数进行更新,得到各阶段更新后的土体参数后验样本。图3给出了结合不同开挖阶段观测数据的土体参数后验分布概率密度函数,图3(a,b)为基于先验分布Ⅰ的后验分布,图3(c,d)为基于先验分布Ⅱ的后验分布。图3中:第3阶段表示结合第3阶段监测数据对土体参数先验分布进行更新后的土体参数后验分布,第4阶段表示结合第3,4阶段监测数据对先验分布进行更新后的土体参数后验分布,以此类推。由图3可以看出:不同先验分布第3,4阶段的后验分布存在显著差异,随着融合监测数据的增多,后续开挖阶段的土体参数后验分布虽然逐渐接近,但仍存在一定的差异。
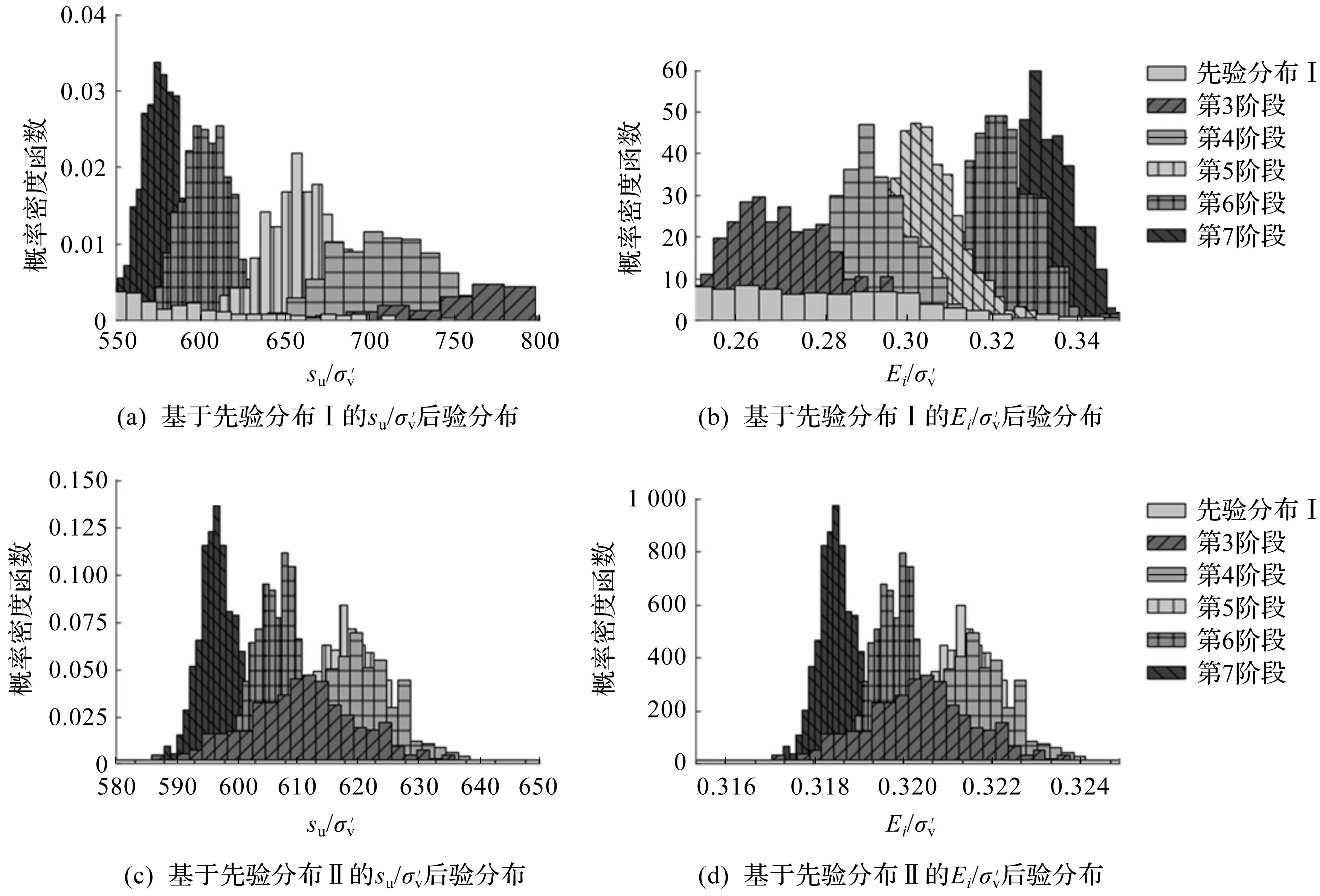
图3 土体参数的先验和后验分布Fig.3 Prioriand Posterioridistributionsofsoilparameters
图4基于不同的先验分布预测了基坑开挖各阶段的最大墙体侧移和最大地表沉降。图4中:三角形、正方形表示不同的先验分布;圆点表示现场观测值;初始、第3阶段、第5阶段分别表示基于先验分布、融合第3阶段观测值、融合第5阶段及之前开挖阶段的观测值,对当前及后续开挖阶段进行变形预测结果的均值。由图4可以看出:基于不同先验分布的初始变形预测略微高估了各阶段的开挖变形,先验分布Ⅰ的预测结果略大于先验分布Ⅱ的预测结果,且不同先验分布之间的差异较大。虽然融合第3阶段观测值的预测结果逐渐靠拢,但仍存在一定的差异。融合第5阶段及之前开挖阶段观测值的预测结果趋于一致,且非常接近现场观测值。
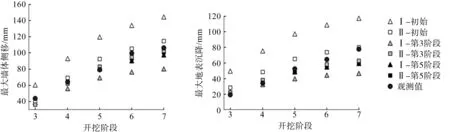
图4 基于先验分布的开挖变形预测Fig.4 Excavation deformation prediction of excavation deformation based on priori distributions
综上,先验分布的选择对基坑开挖变形预测有较大的影响,虽然先验分布的影响会随着融合观测数据的增多而降低,但是在工程实际中,先验信息和现场监测数据都是有限的,因此需要谨慎选择先验分布类型。
2.4 迭代次数对预测结果的影响
图5显示的是使用迭代次数Na分别为1,2,4,8时,结合所有开挖阶段的观测值更新土体参数,基于更新后的土体参数预测第7阶段的最大墙体侧移。箱形图中心实线和三角形分别代表中位数和平均值,箱体底部和顶部对应25和75百分位,上下边缘线表示95%置信区间范围。由图5可以看出:当迭代次数为1时,预测结果与其他迭代次数的预测结果相差较大,随着迭代次数的增加,结果逐渐趋于一致,且预测准确性逐渐提高,预测的95%置信区间逐渐覆盖现场观测值。当迭代次数大于4时,预测均值基本相同,迭代次数对预测结果的影响较小。
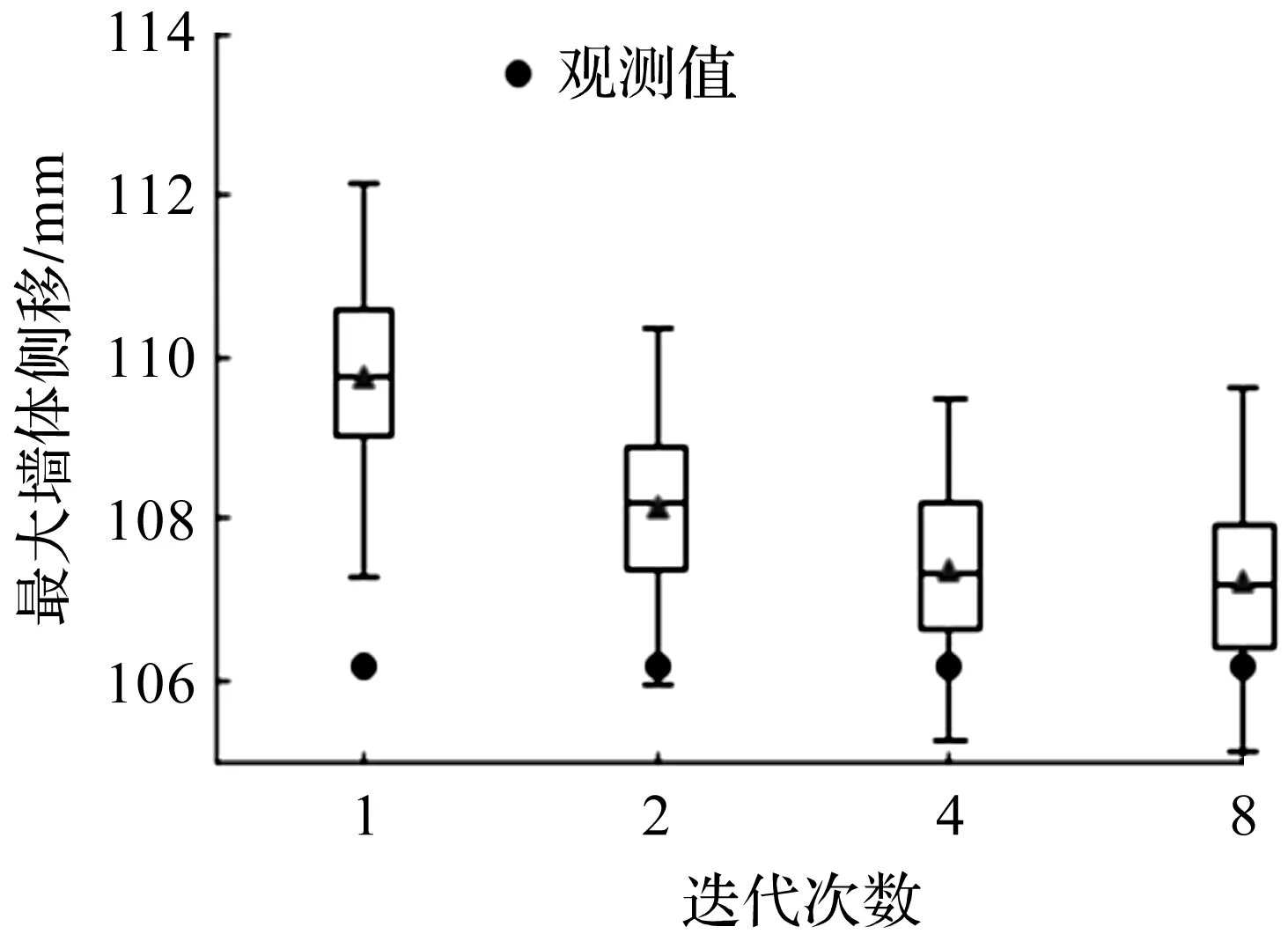
图5 不同迭代次数的最大墙体侧移预测Fig.5 Prediction of maximum wall lateral movementfor different iterations
2.5 样本量对预测结果的影响
在样本量不同的情况下,结合第3阶段观测值进行土体参数更新后,对第7阶段的基坑开挖最大墙体侧移进行预测。样本量分别设置为10,50,100,500,1 000个,每个样本量进行了20次不同的运算,取每次运算的均值绘制误差棒图,三角形表示均值,误差条表示两倍标准差。不同样本量的最大墙体侧移预测如图6所示。由图6可以看出:当样本量为10个时,预测均值和现场观测值偏差较大,且20次运算结果的标准差较大。当样本量逐渐增加,预测均值向现场观测值靠拢,且当样本量大于50个时,样本量对预测均值的影响较小。对于TNEC工程的基坑开挖变形预测,当样本量大于500个时,持续增加样本量对预测均值和置信区间影响较弱,因此,样本量为500个是较为适合该工程的值。
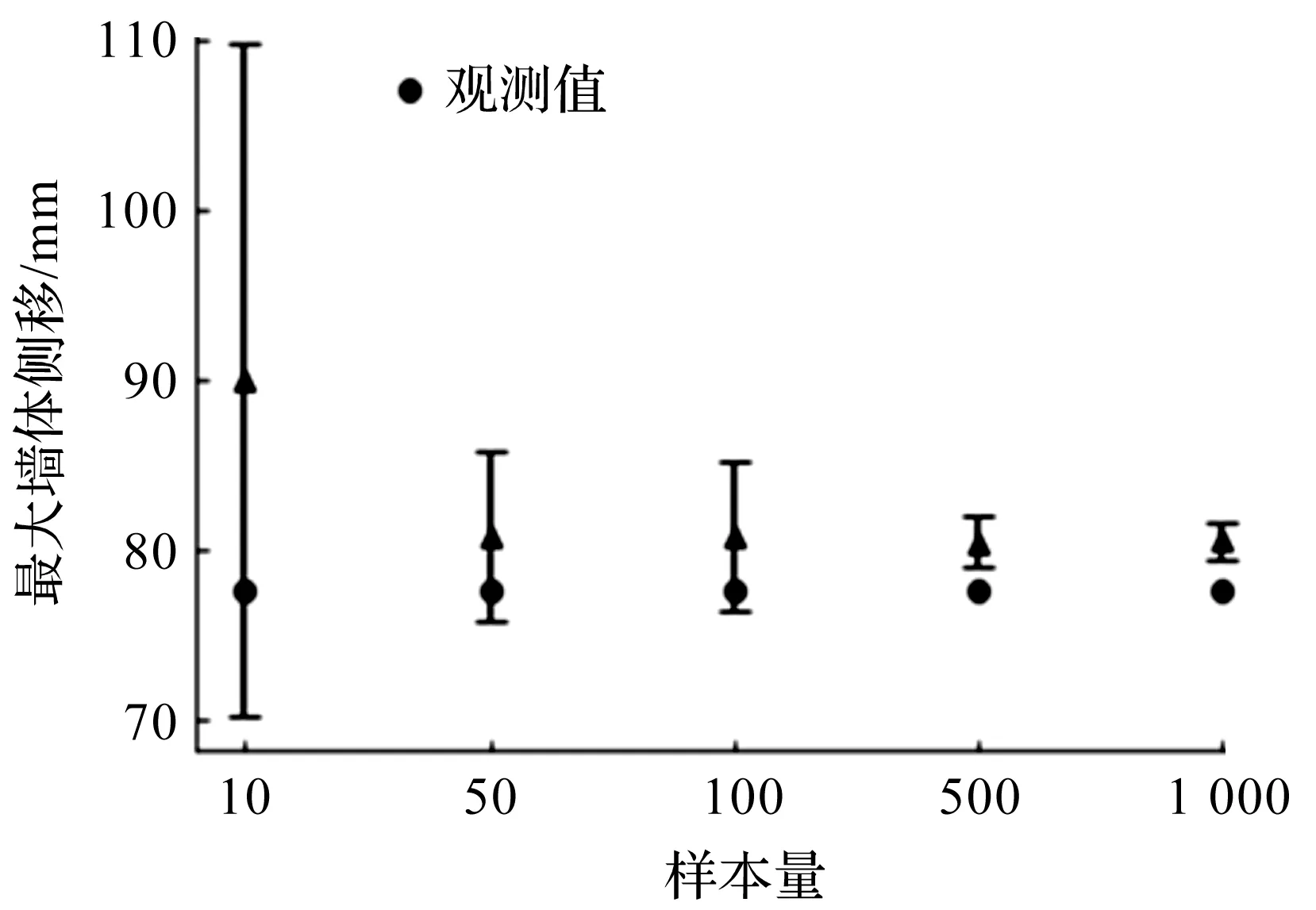
图6 不同样本量的最大墙体侧移预测Fig.6 Prediction of maximum wall lateral movementwith different sample sizes
3 结 论
笔者提出一种同时预测基坑开挖最大墙体侧移和最大地表沉降的概率反分析方法,将其应用于台北TNEC基坑开挖工程,说明了笔者方法的有效性,并研究了先验分布类型、融合不同开挖阶段的观测数据、迭代次数以及样本量对预测结果的影响。结果表明:假设先验分布服从对数正态分布得到的TNEC开挖变形预测结果略大于采用均匀分布时的预测结果;融合更多不同开挖阶段的观测数据,可以有效提高预测的准确性;随着迭代次数的增加,虽然预测准确性逐渐提高,但当迭代次数大于4时,迭代次数对预测结果的准确性影响较小;随着样本量的增加,预测结果的准确性在整体趋势上不断提高;虽然当样本量从10增加到50时,预测结果的准确性显著提高,但是当样本量大于500时,持续增加样本量对预测结果的影响较弱。
