基于循环神经网络的盾构姿态及掘进参数预测
2023-11-30曾志全张亚鹏杨长松曾少翔
吴 坚,曾志全,张亚鹏,刘 龙,杨长松,曾少翔
(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;2.浙江工业大学 土木工程学院,浙江 杭州 310023)
随着城市的发展,隧道建设工程增多,盾构法因不影响地面交通、机械化程度高等优点而得到广泛运用。盾构姿态是盾构施工过程中需要严格控制的参数。盾构姿态控制不良将导致过大的地表沉陷、管片开裂、铺设轨道和隧道贯通困难等问题。目前盾构姿态的预测和控制缺乏系统完善的理论支持,主要依赖于经验关系,尤其对于复杂地质条件下的盾构姿态预测是比较困难的[1]。复杂的地质施工条件会引起土体应力状态变化,从而导致盾构偏离设计轴线,因此复杂地质条件下盾构姿态的预测成为盾构掘进控制的核心问题。为了解决盾构姿态精准预测问题,国内外部分学者从理论公式、运动学原理方向对盾构姿态预测进行探究。沈翔等[2]建立用于预测盾构机掘进过程中俯仰角的理论公式。Sramoon等[3]为了模拟开挖过程中的盾构姿态的变化,建立了盾构姿态动力学模型。然而,上述方法由于不同环境工况的限制,需要做出大量的假设,无法对未来发生的工程风险进行防控。近年来,随着计算机技术的飞速发展,机器学习、深度学习在各个领域得到广泛应用,许多学者开始将机器学习算法应用于盾构姿态的预测。张爱军[4]基于BP神经网络模型,对上软下硬复杂地层下的盾构姿态进行预测。Wang等[5]基于XGBoost预测模型,实现硬岩地层条件下轴姿态预测。吴惠明等[6]基于支持向量机算法,提出了一种预测盾构姿态偏移与优化施工参数的方法。李增良[7]提出了基于LSTM-SVM的深度组合预测模型,证明了其对盾构俯仰角的预测优于传统方法。以上研究大多侧重于对盾构竖直方向进行预测,对水平方向的偏移量研究较少。此外,盾构总推进力是决定盾构机工作效率的一个重要参数,对于盾构机的运行成本和安全性有重大意义。盾构姿态偏差过大,将导致总推进力变大,需要调节总推进力和各类参数来达到减小姿态偏差的目的。Gao等[8]利用LSTM预测盾构机稳定运行阶段的刀盘扭矩和总推力。Chen等[9]开发了一个基于粒子群优化(PSO)和门控递归单元(GRU)神经网络的混合模型来预测和分析盾构刀盘扭矩。一些学者在智能算法方面研究了重要的施工参数。然而,这些研究很少考虑同时预测盾构机姿态和施工参数。鉴于此,提出了基于两种循环神经网络(LSTM和GRU)同时预测盾构水平姿态和总推进力的方法,具体研究内容包括数据清洗与降噪、地层参数重构、超参数优化以及两种预测模型的对比。
1 机器学习模型
1.1 长短期记忆神经网络
长短期记忆网络(LSTM)可以解决传统循环神经网络因信息传播距离过远而导致的梯度爆炸或消失问题。LSTM通过“门”来控制取舍信息,以实现遗忘或记忆的功能。一个LSTM单元有3个门,分别为遗忘门、输入门和输出门[10]。

图1 长短期记忆网络示意图Fig.1 Structure of long short-term memory network
遗忘门:因为遗忘门会为每一项产生一个0~1的值(0代表遗忘,1代表记忆),所以其可以决定上一状态的遗忘程度。计算式为
ft=σ(wf·[ht-1,xt]+bf)
(1)
式中:t为时间;σ为sigmoid函数;wf,bf分别为遗忘门中的权重和偏置。
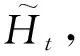
it=σ(wi·[ht-1,xt]+bi)
(2)
(3)
式中:wi,bi分别为输入门中的权重和偏置;wc,bc分别为记忆细胞中的权重和偏置。
输出门:输出门同样会为每一项产生一个0~1的值,用于过滤信息。计算式为
ot=σ(wo·[ht-1,xt]+bo)
(4)
ht=ot·tanh(Ht)
(5)
式中wo,bo分别为输出门中的权重和偏置。
综上,LSTM的3个门是通过3个0~1的数值来有选择地过滤保留旧的信息、新加入的信息和当前单元状态的全部信息的操作。
1.2 门控循环单元
门控循环单元(GRU)是LSTM模型的一种变体,它将遗忘门和输入门合并成更新门,同时将记忆单元与隐藏层合并成了重置门,不仅让整个结构运算变得更加简化,而且降低了过拟合的风险[11]。
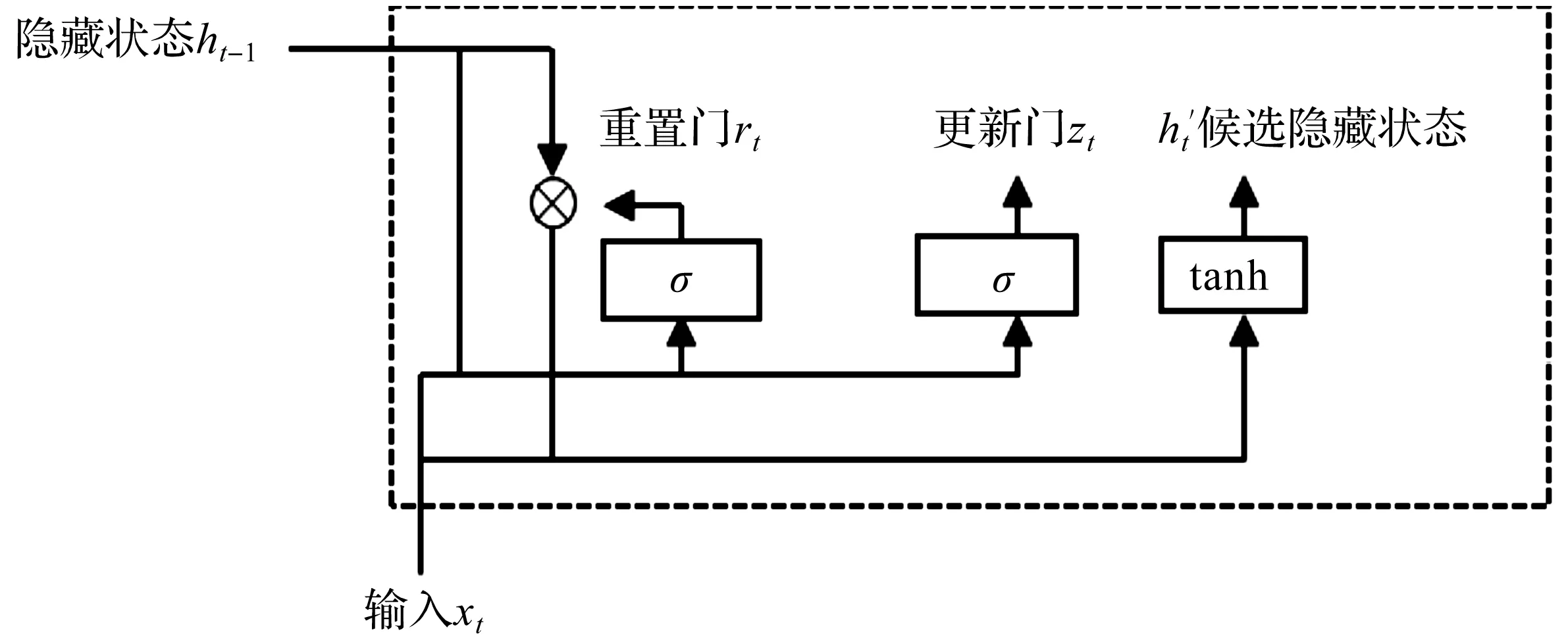
图2 门控循环单元示意图Fig.2 Structure of gated recurrent unit networks
更新门:主要决定保留多少信息。计算式为
zt=σ(W(z)xt+U(z)ht-1)
(6)
式中:W为与输入数据相乘的权重矩阵;U为与隐藏状态相乘的权重矩阵。
重置门:主要决定需要被遗忘信息的数量。计算式为
rt=σ(W(r)xt+U(r)ht-1)
(7)
当前记忆内容:新的记忆内容使用重置门,用于存储相关的信息。计算式为
h′t=tanh(Wxt+rt·Uht-1)
(8)
当前时间步的最终记忆:zt与ht-1对应元素的乘积(表示前一时间步保留到最终记忆的信息)加上最终记忆信息。计算式为
ht=zt·ht-1+(1-zt)·h′t
(9)
2 数据库建立
2.1 工程实例
本工程西起之浦路以西,东至复兴路,全长约6.3 km。西段项目部施工范围为K0K2+805,西起梅灵南路,东至3#工作井(浙江大学之江校区足球场)。其中盾构隧道长度约2.65 km,隧道开挖直径15.03 m,管片外径为14.5 m,管片内径为13.3 m,管片厚度0.6 m。隧道最大纵坡1.75%,最小转弯半径750 m,最小覆土8.40 m,最大覆土21.88 m,隧道双线全长2 652 m。
盾构段分南北线,南线盾构自2#工作井始发,至3#工作井接收,起始里程为K1+544,终点里程为K2+776,单线隧道长1 232 m,共617环。北线隧道自1#工作井始发,至3#工作井接收,起始里程为K1+358,终点里程为K2+776,单线隧道长1 418 m,共709环。
2.2 数据选取
对盾构姿态及盾构总推进力的预测属于有监督学习[12],有监督学习的每个样本包含输入参数和输出参数(标签)[13]。输入参数包括施工参数和地层参数,输出参数包括盾构水平姿态和盾构总推进力。此外,盾构施工是一个连续的过程,此刻的盾构姿态和总推进力也会受到上一时刻的影响,因此将上一时刻的水平姿态和总推进力作为下一时刻的输入参数。数据来源于杭州市某道路提升工程,选取盾构掘进西段南线第3环到453环作为预测模型数据。选取盾构隧道的刀盘水平偏移、盾尾水平偏移以及盾构总推进力作为输出参数(表1),掘进速度、扭矩以及总推进力等20个参数作为施工输入参数(表2),同时根据地质勘探报告选取地层输入参数。
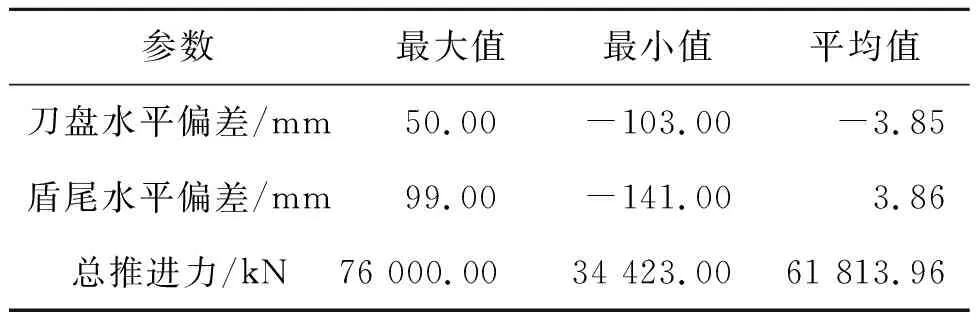
表1 输出参数

表2 输入参数
3 数据重构与预处理
3.1 地层参数重构
在选取的数据中盾构机穿越了不同的地层,如图3所示。
图3 研究项目的典型地质剖面图Fig.3 Typical geological profifiles of the studied project

(10)
式中:aω为相应地质参数测量值的加权平均值;k为隧道开挖断面内地层层数;ϑ为集合中的一个元素;ti为相应岩层的厚度。根据从地质调查报告中收集到的数据,有5个主要的地层参数:单位重度γ、黏聚力c、压缩模量ES1-2、天然含水量w和内摩擦角φ。地层参数示意图如图4所示。
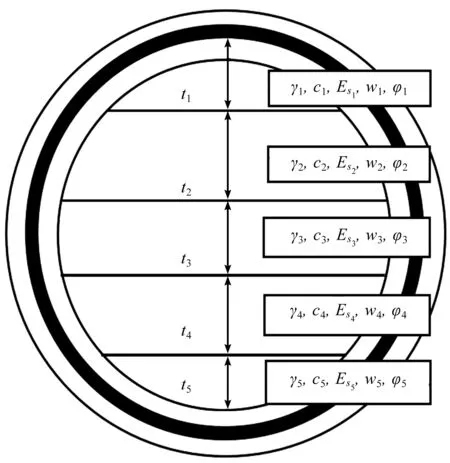
图4 地层参数示意图Fig.4 Soil profile of a tunnel section
3.2 数据预处理
不同地层的物理力学性质会对盾构总推进力和盾构姿态的预测准确性造成很大的影响,同时数据统计过程中有人为记录数据,不可避免地存在误差。利用箱型分析法处理盾构水平姿态和盾构总推进力数据,将离散的异常值进行剔除(图5)。箱型图的中心实线代表中位数,箱体底部和顶部分别对应下四分位(实测数据中有四分之一的数据比它小)和上四分位(实测数据中有四分之一的数据比它大),上下界分别表示极大极小值。箱型分析结果显示盾构刀盘水平偏移量、盾尾水平偏移量、盾构总推进力的异常点数量分别为40,26,12,与数据总数相比,异常数据占比较大,因此不应直接将异常值剔除。这种情况下可以考虑利用随机森林填补法[17]对数据进行补全,然而此类方法适用于数据量较大的情况,笔者研究的数据量较小不宜采用该方法。经过对比各种处理方法的优劣,根据异常值邻近数据的线性关系对其进行补全[7]。
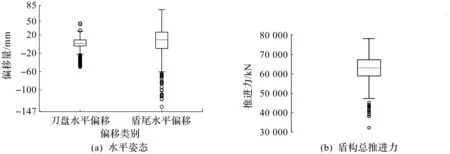
图5 基于箱型分析法的输出参数处理Fig.5 Output parameter processing based on the box analysis method
在箱型分析处理异常点后,因为笔者选取每环数据作为代表值,时间间隔长,数据波动大,所以采用多贝西小波对数据进行重构降噪[18],以达到提高准确率的目的。具体步骤:首先用小波变换对箱型分析处理过的数据进行多频带分解;然后对各频带系数进行去噪处理;最后利用小波变换重构信号得到纯净信号。预处理流程图如图6所示。降噪后的数据如图7所示。
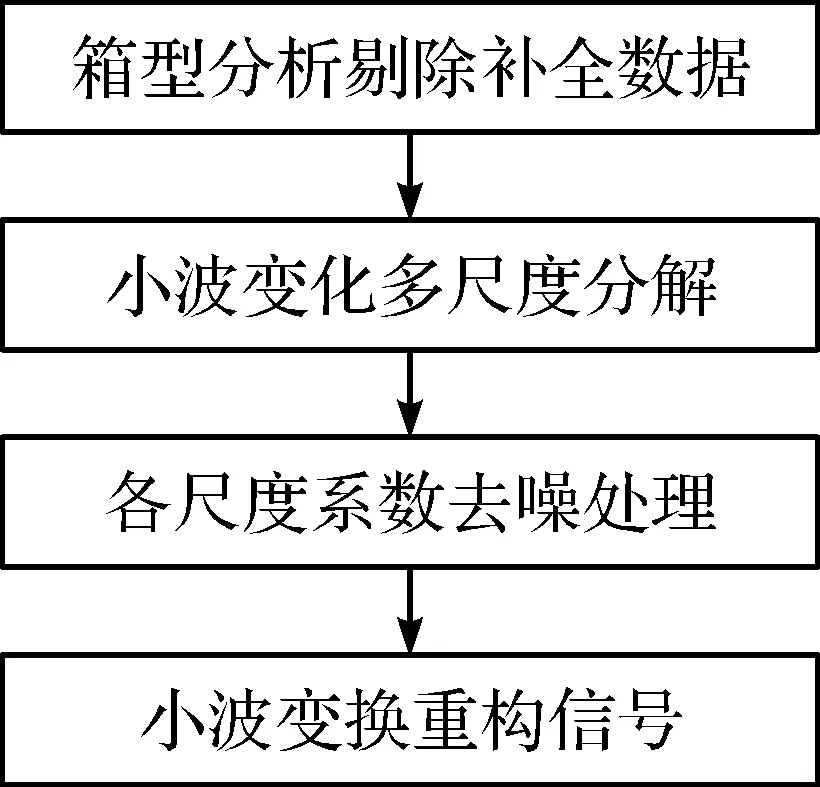
图6 数据预处理流程图Fig.6 Flow chart of data preprocessing
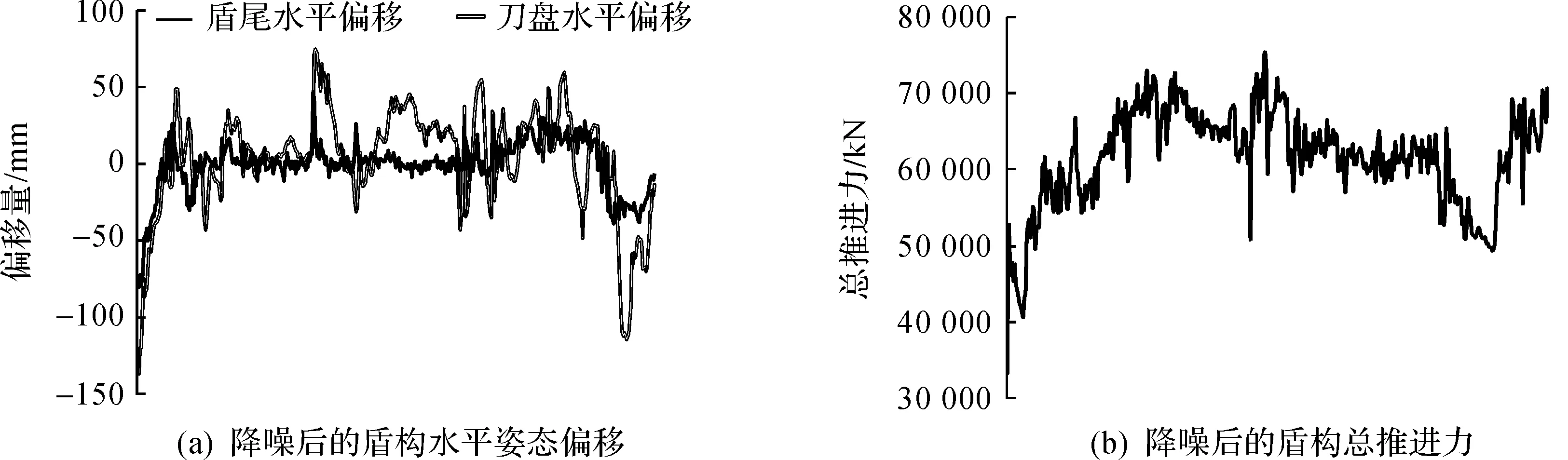
图7 降噪重构后的输出参数Fig.7 Output parameters after noise reduction and reconstruction
因为盾构总推进力的数量级比盾构水平姿态偏移大100倍,计算盾构总推进力的变化时会掩盖掉盾构水平姿态偏移的变化,所以对数据进行归一化以提高模型预测的准确度[13],计算式为
(11)
4 模型建立与结果分析
4.1 模型建立
模型选取西段南线第3环到第363环用于训练,第363到第453环用于测试,即训练集和测试集的占比分别为80%和20%。样本参数为30种,且进行多次验证复核,当设置神经网络实现算法Dropout为0.1时,可以有效防止过拟合;当时间步为3、学习率为0.001时,预测结果最佳。
4.2 模型评价指标
盾构机掘进过程中会遇到各种问题,如复杂的地质地形、地面隆起或沉降变形。当前工程允许对盾构参数的预测有一定的偏差,选取了3个容许等级:=10%,=15%,=25%,如果真实值v和预测值vp满足计算式为
v(1-)≤vp≤v(1+)
(12)
则认为模型在此样本上预测结果准确。评价模型的性能的指标分别为准确率和拟合优度[6],表达式分别为
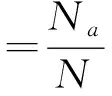
(13)
式中:Na为式(12)中满足容许等级的预测值个数;N为测试集样本总数。
(14)
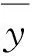
4.3 结果分析
LSTM模型性能如图8所示。图8(a)柱状图表示在容许误差分别为10%,15%,25%的情况下盾构姿态和总推进力预测结果的准确率。由图8(a)可以看出:在25%的容许误差下,LSTM模型对后续90环内的刀盘水平偏移、盾尾水平偏移、总推进力的预测准确率分别为84.2%,72.1%,94.3%,3种盾构输出参数平均预测准确率达到了83.5%,表明建立的LSTM模型预测结果可以有效解决盾构水平姿态控制滞后和盾构掘进效率评估的问题,工程师可以根据预测结果及时调整施工参数。图8(b)柱状图表示数据清洗、数据降噪、数据清洗降噪对LSTM模型预测的效果。由图8(b)可以看出:数据清洗降噪后的模型平均拟合优度最高,达到了0.819,表明对数据进行清洗与降噪能显著提高模型准确预测的能力。
图9对比了基于LSTM模型3种盾构输出参数的预测值和真实值。图9中:R2和A分别表示评价指标拟合优度和25%容许误差下的预测准确率,横、纵坐标分别代表盾构参数真实值和盾构参数预测值。当图9中散点越接近对角线时,表明该散点对应数据的预测值和真实值越接近。图9中3种盾构输出参数的散点均较接近于对角线,因此LSTM模型是一种预测盾构参数的可靠方法,能够较准确地对3种盾构输出参数进行预测。此外,图9(a)散点数据集中于-50~25 mm,图9(b)集中于-100~50 mm,图9(b)相较于图9(a)散点跨越纵坐标值较大。由此可知:盾构机在该施工段掘进过程中,盾尾水平偏移的幅度要大于刀盘水平偏移,因此该施工路段盾尾处更容易出现因盾构姿态偏移带来的一系列危害,工程师在施工时应重点关注该问题。
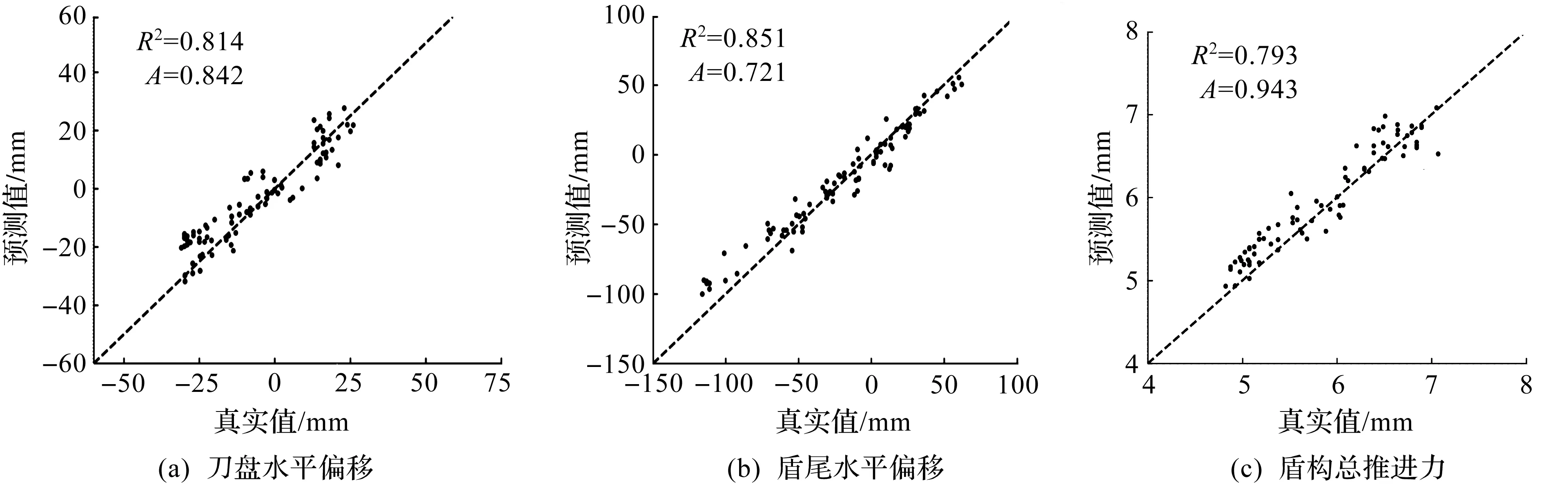
图9 LSTM模型预测值与真实值对比Fig.9 Comparison of the actual value and the prediction of LSTM
LSTM模型与GRU模型预测值对比如图10所示。实线、虚线和点线折线分别表示LSTM对盾构参数的预测值、GRU对盾构参数的预测值以及盾构参数的实测值。由图10可以看出:LSTM模型和GRU模型预测得到的盾构姿态及总推进力曲线和实测曲线整体上基本一致。LSTM模型在刀盘水平偏移、盾尾水平偏移和总推进力上取得的R2均略高于GRU模型,总体来看,LSTM模型在此问题中的预测效果优于GRU模型。此外从第411环到第427环数据可以发现:当盾构姿态偏移增大时,盾构总推进力迅速上升,这表明盾构姿态偏移和盾构总推进力之间存在一定程度上的正相关关系。对盾构水平姿态和总推进力同时预测,如果发现总推进力和盾构姿态偏移同时增大,考虑是由于盾构总推进力增大造成的盾构姿态偏差,此时通过减少总推进力和合理分配左右顶推进力来调整盾构水平姿态;如果预测总推进力在正常范围内,则可能由于推力中心位置不合适造成姿态偏差,此时需要根据工程实际进行检测与调整。
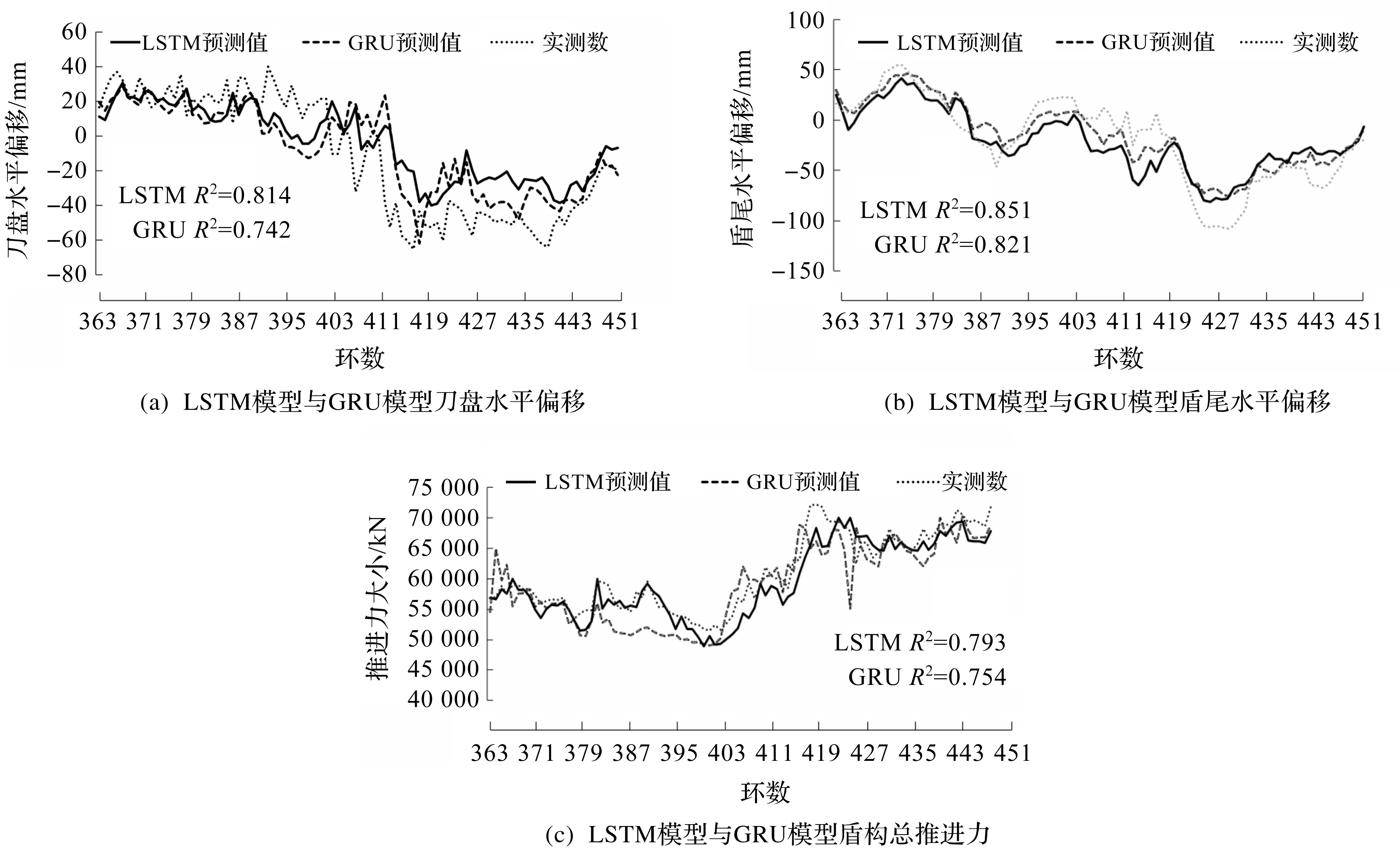
图10 LSTM模型和GRU模型预测对比Fig.10 Comparison of prediction between LSTM model and GRU model
5 结 论
依托杭州某道路提升工程,提出了基于循环神经网络的盾构水平姿态和总推进力预测方法。首先采用箱型分析法清洗原始数据;然后利用多贝西小波变换进行数据降噪;最后以准确率和拟合优度作为评价指标,评估了LSTM和GRU模型在盾构水平姿态和总推力预测的性能。结果表明:采用箱型分析法和小波变换进行数据预处理可有效提高后续建立的模型的预测准确性,相较于GRU模型,LSTM模型预测能力更优,平均准确率为83.5%,平均拟合度为0.819,表明了笔者所提基于循环神经网络的盾构水平姿态和总推进力预测方法的有效性。
