考虑邻跨混凝土徐变收缩差异的连续组合梁次内力分析

韩 春 秀

( 云南民族大学 物理与土木工程系, 云南 昆明 650504 )

0 引 言

混凝土徐变收缩特性对结构长期服役过程产生的影响较显著,尤其是对挠度要求严格的轨道交通梁．作为超静定结构的连续钢-混凝土组合梁,其耦合了截面内外应力重分布现象,使结构内力具有复杂的时间依从性[1-5]．受混凝土浇筑时间差异等因素影响,几乎所有分节段施工的相邻两跨混凝土都存在徐变收缩特性差异的特点,如连续梁不等跨、邻跨混凝土材料特性差异、加载方式不同等,均会导致混凝土与钢梁之间以及组合梁整体与支座之间产生制约性改变,引起支座内力变化．即便是一次成形的连续组合梁,两跨混凝土徐变特性、跨度和荷载差异均会对支座次内力产生不同影响．而徐变收缩通常会降低组合结构刚度,带来约束力降低,这种降低有的有利,有的有害[6]．分析组合梁的徐变收缩次内力效应是为了揭示结构内力变化特征和时间演化规律,预估其对结构可能存在的危害,在设计和使用过程中提供趋利避害的指导．

国内外学者开展了一系列关于混凝土结构徐变收缩的时程效应研究[6-23]．Haensel[7]早在20世纪70年代就系统地建立了组合梁截面内部应力重分布的计算方法体系．周履等[6]在我国较早且较全面地研究了混凝土徐变的结构效应问题,并采用逐步计算法求解了分段悬臂施工合龙成连续梁的徐变内力．樊健生等[8]建立了考虑混凝土收缩、徐变及开裂影响的组合梁长期效应计算模型,并采用逐步计算法进行求解．王文炜等[9]采用随时间变化的换算弹性模量法建立了组合梁增量微分模型,并得到各项力学指标的闭合解．Gattesco等[10]通过有限元模型对连续组合梁进行了长期力学分析．现有计算方法比较有代表性的是增量法、逐步计算法和有限元法[6-10],主要涉及含混凝土的组合结构内部应力、含混凝土单一材料结构的外部内力等单一效应边界条件,较少涉及结构内外耦合的双重力学关系[16-23]．从组合梁徐变收缩效应的耦合力学关系可知,复杂应力产生的核心原因是组合梁内部的变形增量受到外部的约束作用,求解徐变收缩次内力是解决连续组合梁徐变收缩问题的关键．然而,目前国内外针对该问题尚未形成统一计算公式,各国规范也鲜有涉及．本课题组进行了分段施工中发生结构体系变换以及支座沉降引起的徐变次内力计算[11-12],本文在此基础上,对连续组合梁不同跨徐变收缩特性差异引起的力学变化进行分析．

1 连续组合梁的徐变收缩次内力特性

超静定结构受强迫的变形约束影响,会引起结构附加内力,即次内力．考虑徐变收缩效应的连续组合梁的支座内力是一种时变函数(图1),其中,有一部分力为常数,包括弹性内力(弯矩、轴力等)和弹性次内力,弹性内力在组合梁截面形心处不随时间改变,但截面内部分配到混凝土和钢梁各自截面的应力受徐变收缩影响[11,13],则徐变收缩次内力改变进而导致内部应力改变,这部分截面应力重分布可按静定结构的内力分配法求解．支座内力随时间变化的原因是次内力受徐变收缩影响,产生徐变收缩次内力随时间演变(图1)．因此,要使连续组合梁内外复杂的耦合关系得到逐一求解,徐变收缩次内力是突破口．

(a) 连续组合梁受力特征

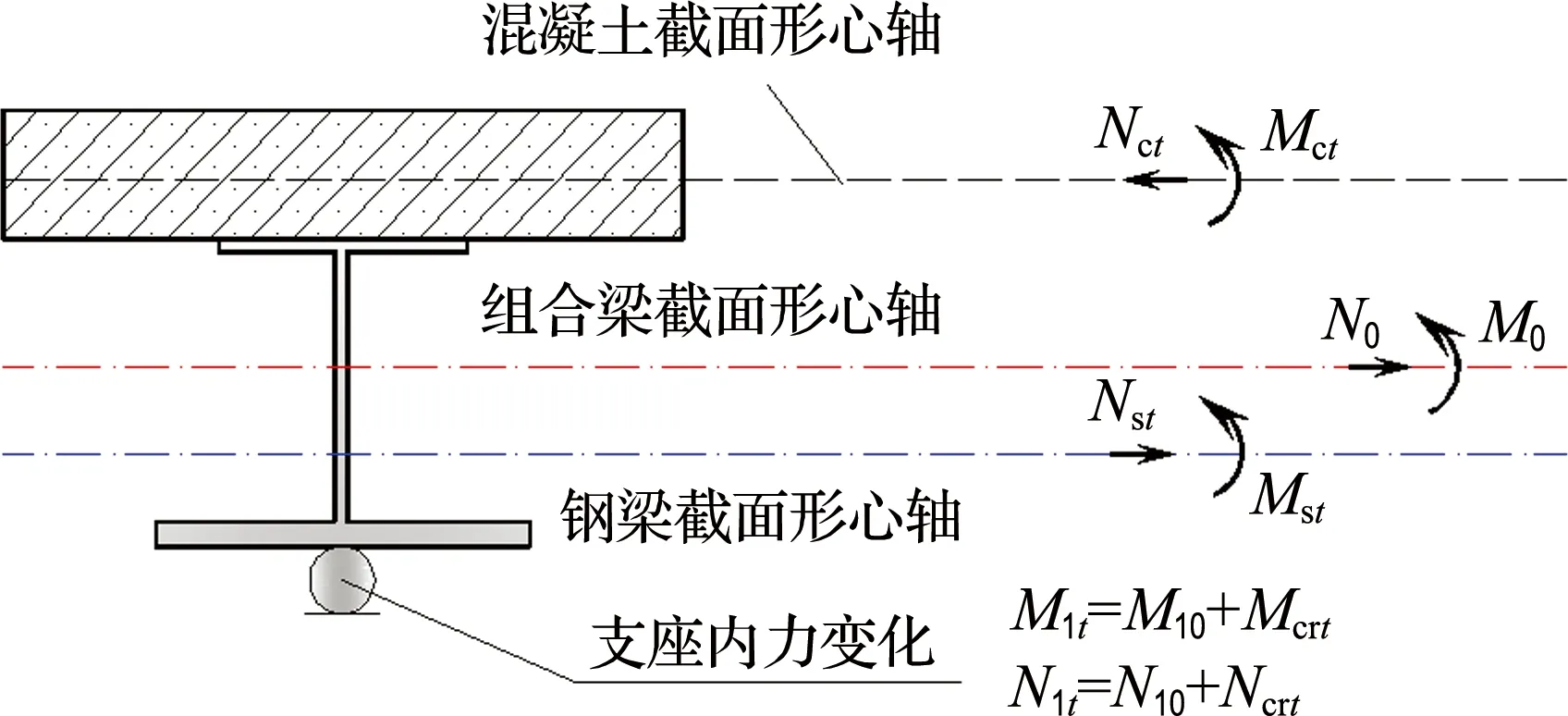
(b) 1-1截面

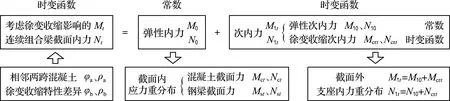
(c) 内力分解

2 邻跨混凝土特性互异的连续组合梁徐变收缩次弯矩推导

2.1 基本体系方程

以两跨连续组合梁为例(多跨情况类似),如图2所示,a、b相邻两跨连续组合梁的混凝土特性不同,即特性互异．跨度分别为la、lb,徐变系数和老化系数分别为φa、ρa和φb、ρb,假设收缩进程与徐变同步[6-7],收缩特性也由徐变特性反映,中间支座两侧转角分别为θa、θb,受自重和荷载g+q作用,下文对中间支座徐变收缩次弯矩进行推导[13]．

在自重和荷载(g+q)、未知力X1作用下连续组合梁的基本体系如图3所示．

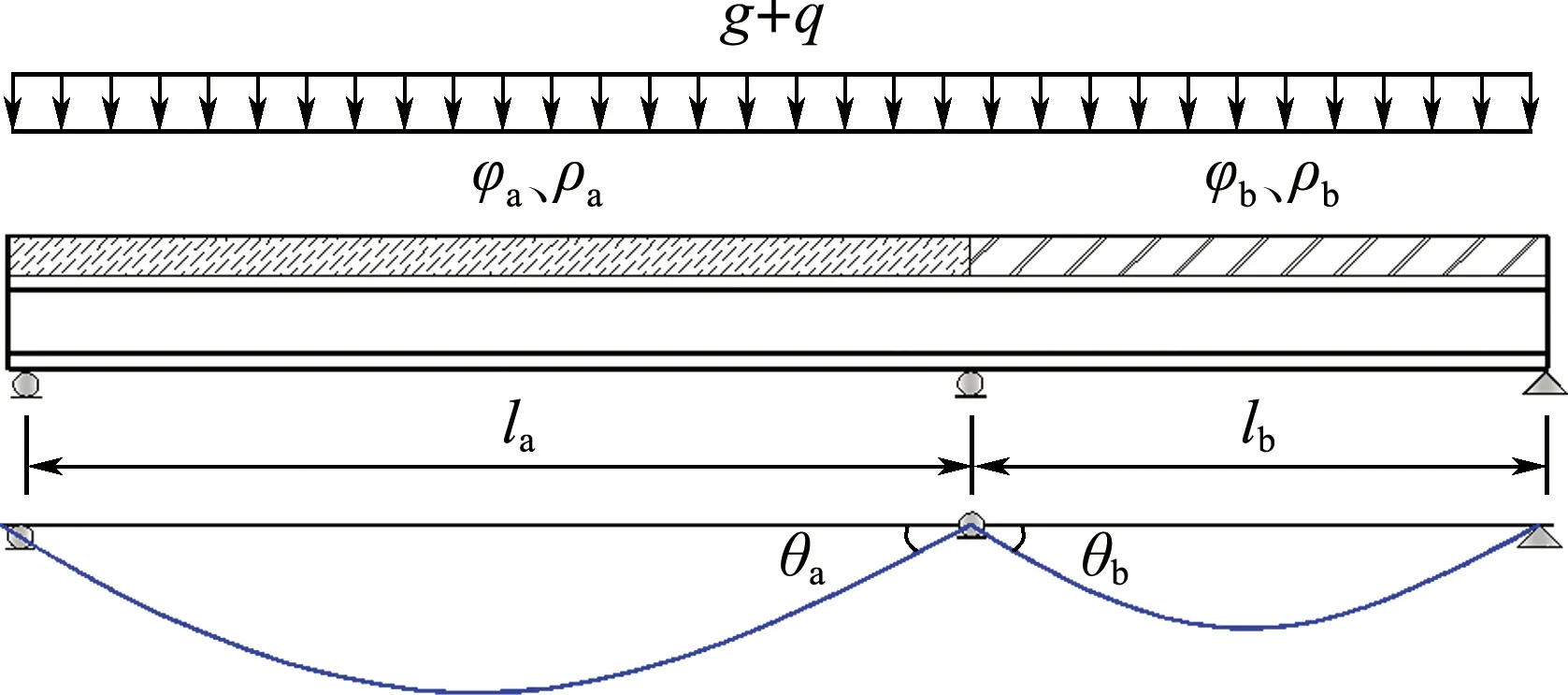
图2 特性互异的两跨连续组合梁

(1)当t=0时,施加荷载,变形条件为

(1)

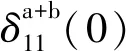
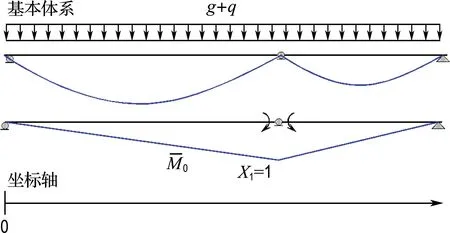
图3 特性互异的两跨连续组合梁基本体系

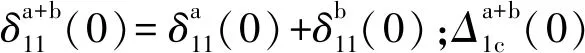
(2)任意t时刻,式(1)转化为

(2)

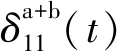
随着组合梁服役时间增加,徐变收缩次弯矩不再是常数,而是时变函数．在任意t时刻,总的次弯矩由常量弹性次弯矩和时变量徐变收缩次弯矩组成,即X1(t)=X1(0)+Xcr(t),则式(2)变为

(3)

2.2 相对转角的徐变收缩特性

本课题组在文献[11]中推导了施工过程因结构体系变换即分段浇筑的简支梁合并成连续梁的徐变次内力,与本文有以下共同点:采用基本假定相同;采用徐变本构方程相同;材料组成相同(图4);截面应力重分布计算模型相同(图5)．因此,本文相对转角计算引入文献[11]中式(32)的计算公式．不同点在于:文献[11]重点解决了前期结构遗留的徐变变形增量受后期结构连续约束后引起的支座内力变化,本文拟重点解决的是相邻两跨梁之间徐变收缩特性不同引起的变形差异导致的支座内力变化．在文献[11]式(32)基础上建立能反映相邻两跨梁因徐变收缩特性差异引起的计算参数,见式(4)～(11)．

图4 组合梁截面材料组成和力学关系

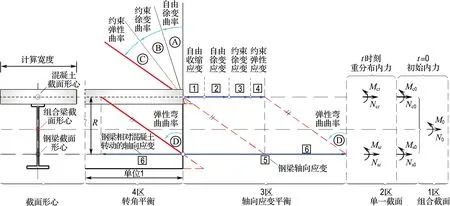
图5 组合梁徐变应力重分布力学计算模型

2.3 相对转角计算

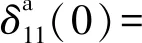
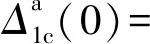
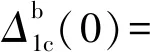
(4)

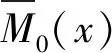
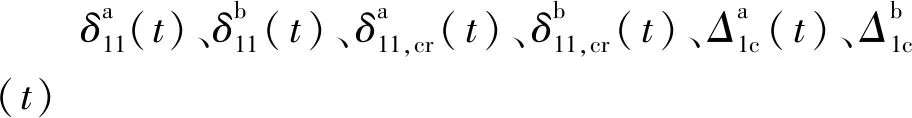
根据文献[11],对于等跨组合梁,对应式(3)相对转角的曲率kt和徐变增量曲率kt,cr为

(5)

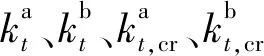
(6)

式(6)中参数的表达式为

(7)

则相对转角为

(8)

2.4 徐变收缩次弯矩计算

将式(8)代入式(3)得

(9)

整理式(9)得

(10)

则徐变收缩次弯矩Mcrt计算为[13]

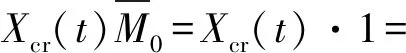
M1t=M10+Mcrt

(11)

式中:Mcrt为t时刻组合梁的徐变收缩次弯矩;M10为初始组合梁的弹性次弯矩;M1t为t时刻组合梁的总次弯矩,以上符号可结合图1进行理解．式(11)中受徐变影响的项与α、αcr相关,受收缩影响的项与β、βcr相关,相应参数表达式见式(5)．

3 邻跨混凝土特性互异的连续组合梁特征分析

3.1 理论分析

(1)类型1:连续组合梁相邻两跨混凝土的徐变收缩特性相同,跨度不等．

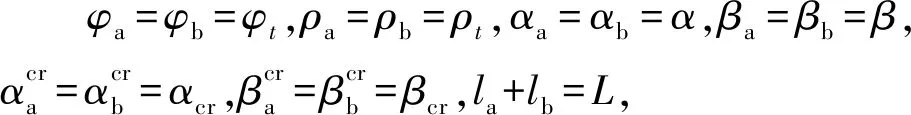
(12)

由式(12)可看出:从结构外部看,连续梁不产生徐变次弯矩,即式(12)第一项为零(这一结论与文献[6]吻合),只产生收缩次弯矩且受系数αcr、βcr和β影响;从截面内部看,同时存在截面徐变和收缩应力重分布且受混凝土徐变系数φt、老化系数ρt、截面内部应力重分布系数ηM和ηN控制,同时影响组合梁应力重分布演化规律．

(2)类型2:连续组合梁相邻两跨的跨度相等,徐变收缩特性不同．

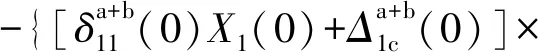
(αa+αb)+[1+X1(0)]L(βa+βb)}/

(13)

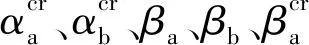
(3)类型3:连续组合梁相邻两跨混凝土的徐变收缩特性不同,跨度也不等．

由式(11)可看出:当连续组合梁相邻两跨混凝土徐变收缩特性互异且跨度不等时,将在支座产生结构外部徐变、收缩次弯矩,次弯矩受徐变次弯矩系数α、收缩次弯矩系数β、考虑老化的徐变次弯矩系数αcr和考虑老化的收缩次弯矩系数βcr影响;同时截面内部发生应力重分布,受系数φt、ρt、ηM和ηN控制,通过式(11)可对任意时刻连续组合梁截面双重力学耦合的情况进行解析计算,进一步获得组合梁受徐变收缩影响下随时间变化的力学演化规律．

(4)类型4:连续组合梁相邻两跨混凝土的徐变收缩特性不同,荷载也不同．

由式(11)可看出:当连续组合梁相邻两跨混凝土徐变收缩特性互异且荷载不同时,将在中间支座产生结构外部徐变、收缩次弯矩,次弯矩特性以及截面应力分布特性与类型3相似．

3.2 算例分析

如图6所示,某连续组合梁有4种工况类型．假设t0=28 d,截面参数如下:Ec=34 500 MPa,Es=210 000 MPa,Ic=101.25×108mm4,Is=486×106mm4,Ihf=2 197.67×108mm4,不考虑收缩,分别计算各组合梁中间支座的徐变次弯矩．

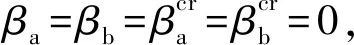
(a) 类型1:不等跨,徐变特性相同

(b) 类型2:等跨,徐变特性不同

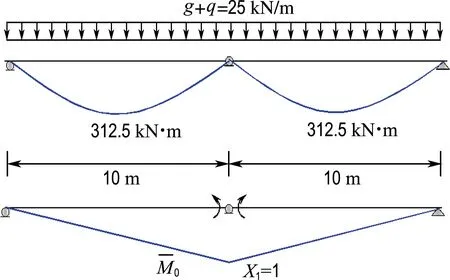
(c) 类型3:不等跨,徐变特性不同

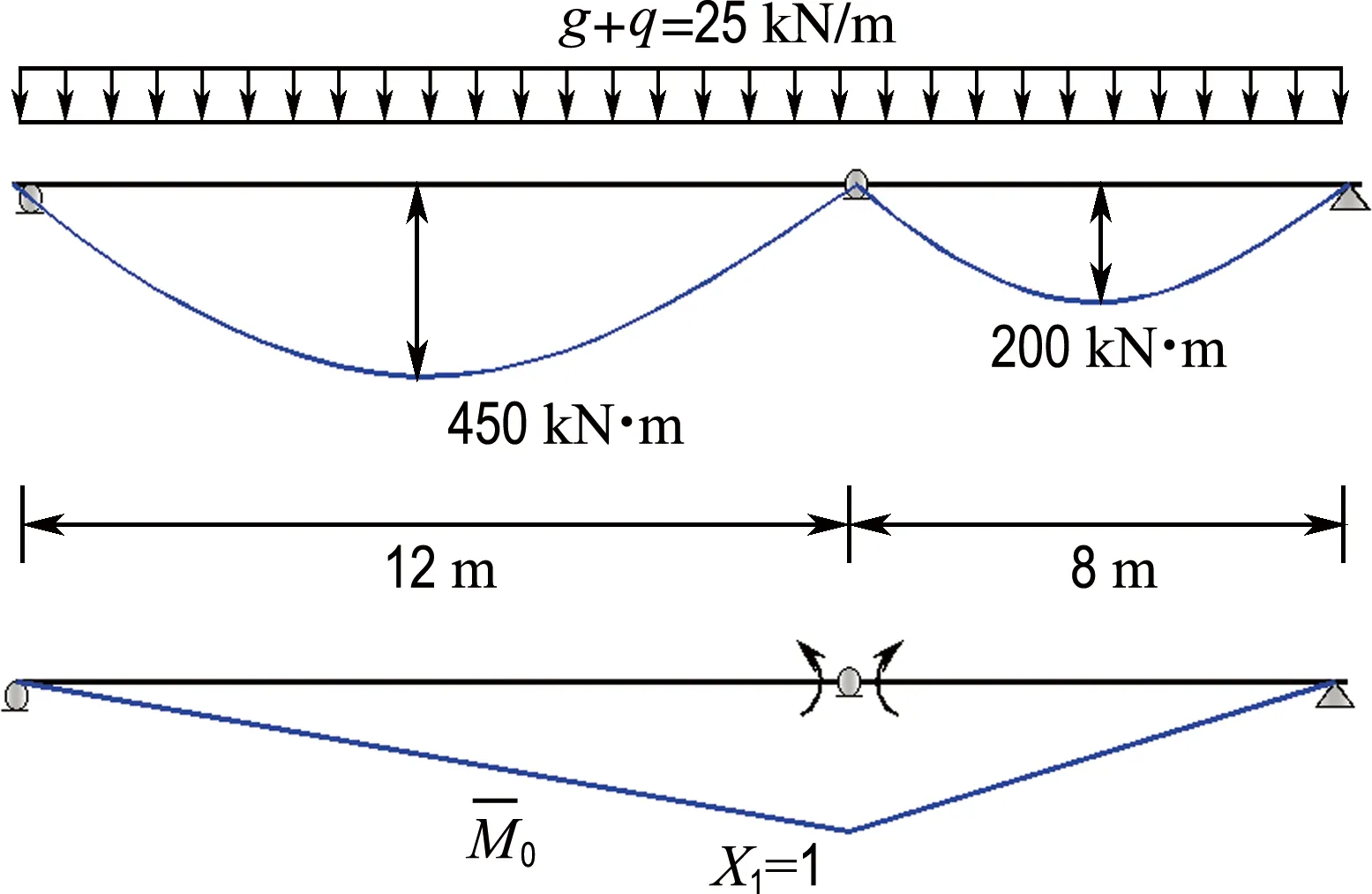
(d) 类型4:荷载不同,徐变特性不同

从表中的算例结果可知[13]:

(1)类型1,两跨连续组合梁邻跨混凝土徐变特性相同,跨度不等,中间支座的徐变次弯矩为零．

(2)类型2,两跨连续组合梁邻跨有相等跨度,混凝土徐变特性不同,中间支座的徐变次弯矩为零．

(3)类型3,两跨连续组合梁邻跨有不等跨度和徐变特性差异,中间支座产生随时间变化的徐变次弯矩Mcrt,支座负弯矩从-350.00 kN·m变化到-364.66 kN·m,变化量为4.2%．徐变次弯矩的变化程度与两跨的跨度差(la-lb)、徐变系数差(φa-φb)、老化系数差(ρa-ρb)等因素有关,内力的重分布从两跨中徐变大的一侧向徐变小的一侧转移,两跨的徐变特性差异越大,重分布值越高,徐变次弯矩越大;反之越小,当两跨的徐变特性相同时,支座徐变次内力为零,即类型1．

(4)类型4,两跨连续组合梁邻跨的荷载和徐变特性均不同,中间支座出现随时间变化的徐变次弯矩Mcrt,支座负弯矩从-156.25 kN·m变化到-175.97 kN·m,变化量为12.6%．徐变次内力的变化程度与两跨的荷载差(ga+qa-gb-qb)、徐变系数差(φa-φb)、老化系数差(ρa-ρb)3个因素有关,内力调整规律同类型3．

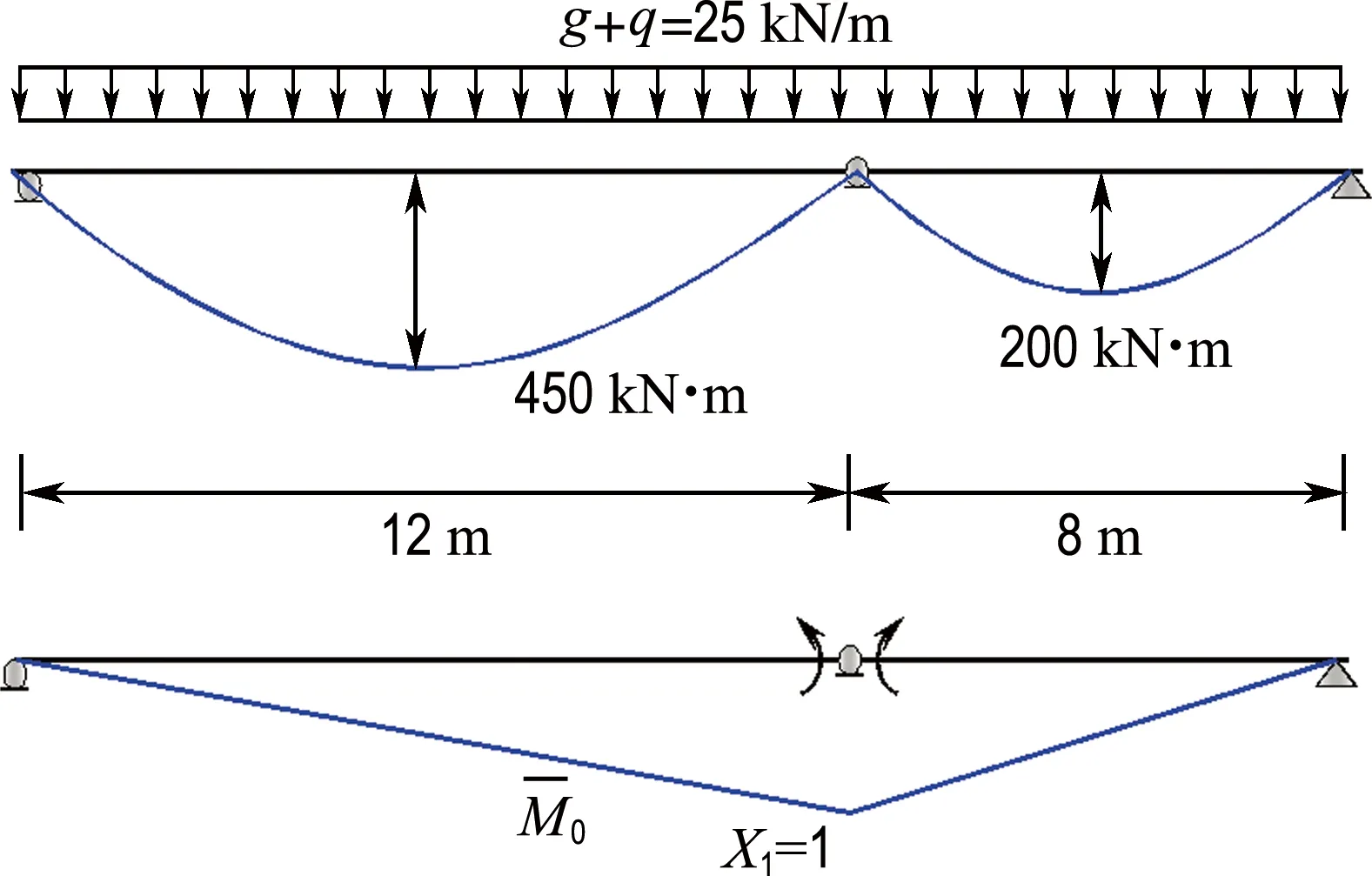
(a) 类型1

(b) 类型2

(c) 类型3

(d) 类型4

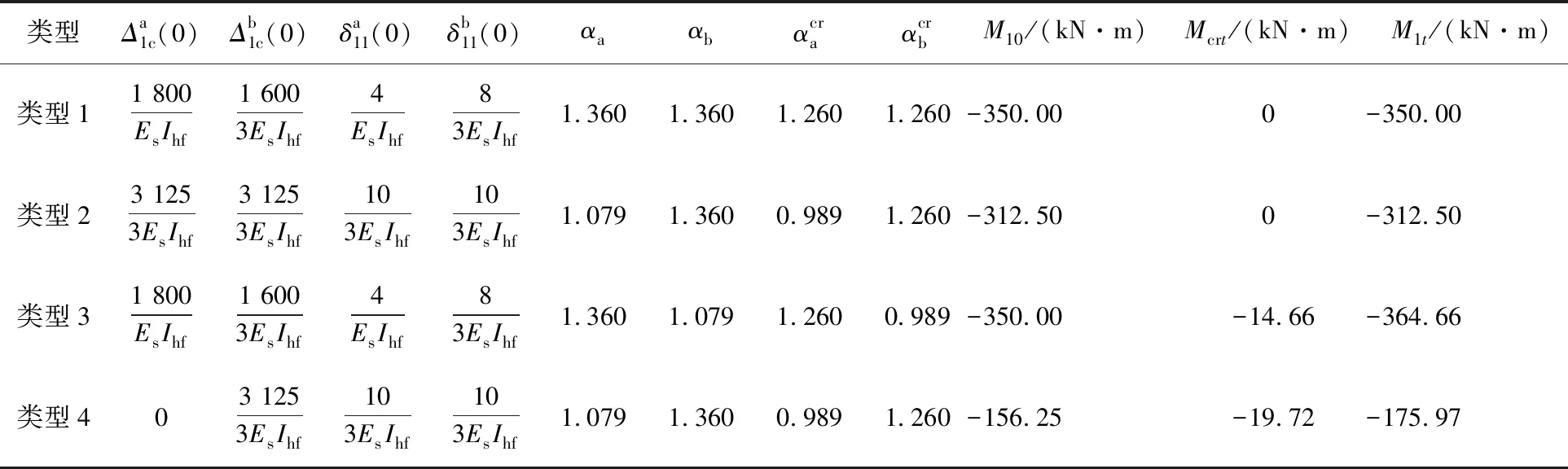
表1 不同工况下组合梁徐变次弯矩计算

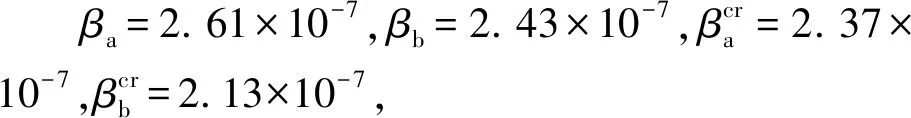
4 结 论

(1)不考虑收缩影响,两跨连续组合梁邻跨混凝土徐变特性或跨度相同,中间支座徐变次弯矩为零;邻跨徐变特性和跨度均不同,或邻跨徐变特性和加载方式均不同,中间支座出现随时间变化的徐变次弯矩．考虑收缩影响,所有特性互异情况均产生收缩次弯矩．

(2)支座次弯矩的变化程度与两跨的徐变系数差、老化系数差、跨度差、荷载差等因素相关,内力的重分布从两跨中徐变大的一侧向徐变小的一侧转移,两跨的徐变特性差异越大,重分布值越高,徐变次弯矩越大;反之越小,当两跨的徐变特性相同时,支座徐变次内力为零．支座次弯矩大小受截面内部应力重分布影响,不仅与混凝土徐变系数、老化系数有关,还受重分配系数影响．

(3)采用本文方法对连续组合梁受截面内和结构外双重耦合的内力进行解析,可获得支座次内力的时程演化规律,公式的参数可编制成表格,便于工程应用．