超深硬岩地层井壁失稳的动力学分析模型：本征频率和高应力的影响1)

2023-11-29卢运虎朱婧宇

力学与实践 2023年5期

卢运虎金衍夏阳朱婧宇

*(中国石油大学（北京）油气资源与工程全国重点实验室，北京 102249)

†(中国石油大学（北京）石油工程学院，北京 102249)

塔里木盆地油气埋深普遍超过6000 m，是超深油气勘探开发的重要领域，具有地层埋藏深、高温、高应力、高孔隙压力、岩石单轴抗压强度大于120 MPa 等特点，属于典型的硬岩地层。钻井过程中，起下钻、钻柱由静止到旋转等操作导致井筒压力发生波动，井壁围岩易发生坍塌掉块，呈现突发与频发等特征，严重制约了超深硬岩地层安全钻井[1]。

前人在井壁稳定模型方面开展了大量的研究工作，为常规地层控制井壁失稳的钻井液密度与性能设计提供了重要依据，主要体现为两方面[2-3]：（1）弹塑性力学模型，仅考虑平面应变以及各向同性介质的应变问题[4]，建立了井眼钻开后长时间尺度下井壁围岩应力分布公式，结合岩石破坏准则，分析井壁围岩稳定性，属于静力学范畴；（2）孔隙弹性力学模型，建立了井眼钻开后小时间尺度下流体与固体耦合引起的井壁围岩孔隙压力与应力动态演化公式，并未对应变和位移进行计算，偏重钻井流体传质过程中拟稳态受力分析。上述两类主流模型应用较广，能在一般地层中获得相对精确的计算结果。后人在此基础上，根据地层的特殊情况对模型做出相应的改进，使其能较好地应用于超深复杂地层。文献[5-7]针对深部地层高温现象引起的热传递、热对流效应的影响，在弹性力学模型基础上建立了温度场–孔隙弹性模型；文献[8-12]针对水化膨胀严重的深部地层，以孔隙弹性力学理论为基础，建立了钻井液化学–孔隙弹性力学模型。这些模型可以使得特殊地层的井壁稳定性分析结果更精准，针对性更强，但仍然属于静力学范畴。然而，超深地层井筒压力波动诱发的井壁失稳问题是短时间的应力扰动问题，属于动力学范畴[13-15]，上述基于弹塑性、孔隙弹性理论以及针对深部特殊地层的井壁稳定模型并不能描述流体与固体的惯性效应，无法给出井筒压力波动条件下井壁围岩应力波传播及其对井周应力分布的规律[16]，考虑流体与固体的惯性效应的动力学模型才能反应超深部地层井壁稳定性的本质。

近年来，国内外学者考虑流体与固体的惯性效应，建立了孔隙弹性动力学的井壁稳定力学模型。滕学清等[17]和Xia 等[18]在Biot 孔隙弹性力学理论基础上，建立了孔隙弹性动力学模型，研究了应力场分布不均匀的地层钻开后各应力随时间变化的分布状态。夏阳等[19]着重研究了卸载过程井壁围岩应力分布公式，Meng 等[20]研究了应力状态、破坏准则、井筒渗透性等因素对井壁围岩坍塌压力的影响规律，进而分析井壁围岩稳定性。上述研究为井壁稳定动力学失稳提供了理论基础，但是对于高应力与井壁围岩力学属性影响井壁坍塌掉块的本质研究较少，井壁围岩力学性质与井底压力波动频率的内在机制不清楚，不能解释井筒压力波动下超深硬岩井壁围岩突发性失稳的力学本质。本文主要研究塔里木盆地超深致密砂岩地层岩石力学变形破坏特征，基于Biot 饱和多孔介质弹性动力学理论[21-22]，在考虑孔隙流体和硬岩的压缩性、惯性及黏滞耦合作用的同时，建立井筒压力波动条件下井周应力分布公式，提出井壁围岩坍塌指数的孔隙弹性动力学预测方法，分析地层本征频率与高应力对井壁失稳的影响规律，揭示超深硬岩地层井壁失稳动力学本质，为钻井过程中井筒压力控制参数调整提供科学依据。

1 工程地质力学特征

塔里木盆地某井6000 m 以深地层发育褐红色致密砂岩，局部发育裂缝，属于低孔低渗地层，见图1。通过井下取芯（6691.6～6691.8 m），参考国际岩石力学学会推荐实验标准，开展了室内单轴和三轴条件下岩石强度实验，获得岩石变形破坏特征及力学参数，如表1 所示。实验研究发现，随着围压的增大，致密砂岩岩石抗压强度逐渐增大，弹性模量逐渐增大，泊松比先逐渐增大再逐渐减小。根据实验结果绘制岩石应力–应变曲线，如图2 所示。实验结果表明：岩石强度高，在单轴强度188.4 MPa，围压80 MPa 条件下岩石强度高达748.5 MPa。观察单轴实验曲线发现，岩石呈现脆性，塑性阶段不明显；随着围压的增大，岩石在弹性极限之后需经历更长阶段的塑性变形达到峰值强度；观察应力–应变全曲线发现，在致密砂岩破裂之后，曲线趋于平稳并获得致密砂岩残余强度，且在较低围压范围（10～60 MPa）内，围压越大，残余强度越大。

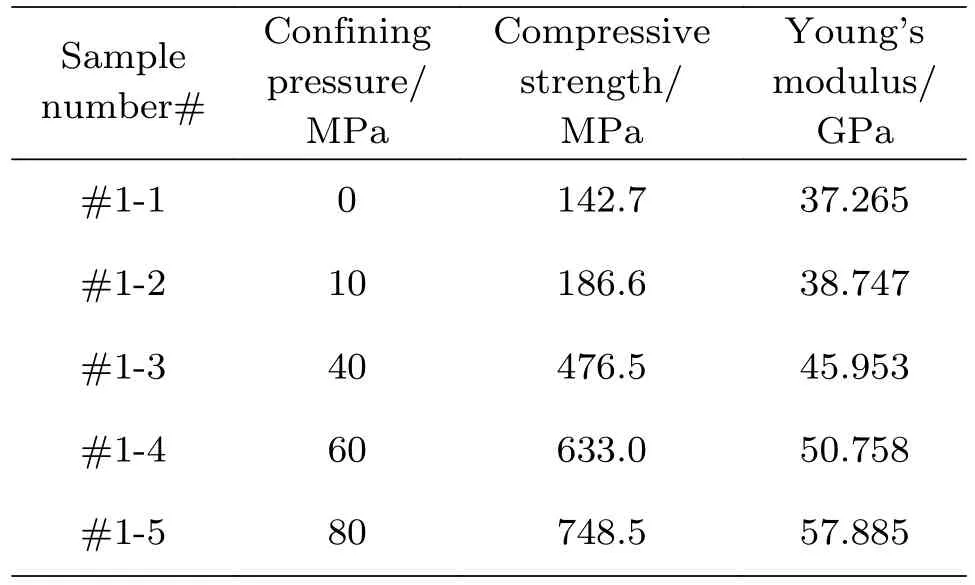
表1 KES2-2-1 井6691.6～6691.8 m 致密砂岩三轴实验数据Table 1 KES2-2-1 Well 6691.6～6691.8m tight sandstone triaxial experimental data

图1 KES2-2-1 井6691.6～6691.8 m 致密砂岩地层成像测井及全尺寸致密砂岩岩心图片Fig.1 KES2-2-1 Well 6691.6～6691.8 m dense sandstone formation imaging logging and full size dense sandstone core images

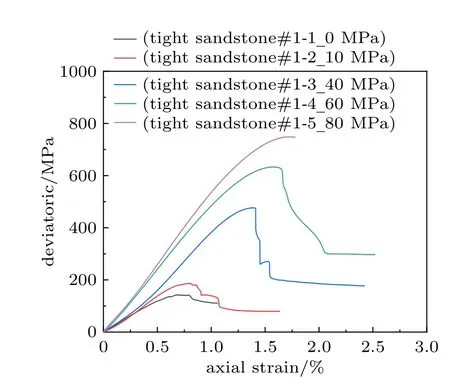
图2 6691.6～6691.8 m 致密砂岩地层三轴应力应变曲线Fig.2 Triaxial stress-strain curve of 6691.6～6691.8 m tight sandstone formation

地层岩石本身亲水，毛细管力作用阻碍油基钻井液流入地层，假设油基钻井液完全不进入地层基质。对于岩石基质内部流体，认为地层渗透率各向同性，孔隙内地层流体饱和。打开井壁瞬间，地层内部流体与固体之间发生强烈的流体–固体相互作用，因此采用横观各向同性流固耦合模型。

式中，ε 表示应变量，u表示固体的位移矢量，下标r，θ 和z分别用来表示径向、切向和垂向3个方向。

为了得到井筒总应力分布，应采用合理的边

2 模型与方法

2.1 模型假设与边界

为了得到动态载荷作用下井筒周围应力分布的控制方程，应当使用孔隙弹性力学方面的基本知识。通常的方法是将应变–位移变化关系，多孔弹性介质中的运动方程、连续性方程以及胡克定律等结合起来，从而生成孔隙弹性动力学模型的控制方程[23]。

本文的主要假设如下：（1）岩石是均匀的、连续的，且力学性质各向同性。该假设可以把力学量表示为固体点的坐标的连续函数，应用一般的数学分析方法；（2）井周岩石只发生小变形且井筒直径远小于施工井段长度。该假设不考虑井眼轴线方向的应变，可将该问题简化为垂直于井筒轴线的平面应变问题；（3）井筒视为规则的圆柱体，应力作用于圆柱面上。该假设可简化分析，便于模型求解。在孔隙弹性地层中钻得的垂直井眼，特征为非流体静力学水平原位应力场，如图3 所示。所以，可将该问题看作是极坐标系下的非对称平面应变问题[24]，用于描述孔隙弹性地层的瞬态位移矢量为：u=（ur，uθ）和w=（wr，wθ），u和w分别是固体和流体的位移，下标r和θ 分别指径向和切向分量。

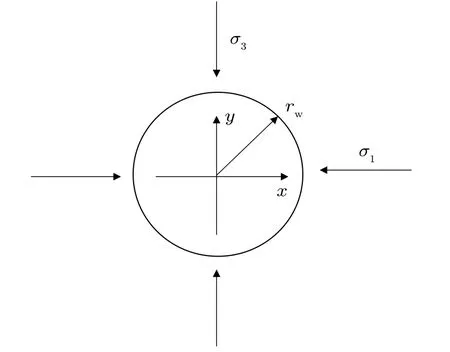
图3 应力作用简图Fig.3 Stress action diagram

相关应变–位移关系式为界条件。底层内边界，即井周边界各应力和孔隙压力条件为

2.2 基本控制方程

在Biot 理论中，单位体积的孔隙流体增量定义为

其中，w表示液体的位移矢量。

相关的岩石应力张量以及孔隙压力的本构方程为

式中，σ 表示地层的应力张量，ε 表示地层的应变张量，μ为泊松比，λ 为拉梅常数，α 和R是Biot 模量系数（其中α 满足，其值的大小表征地层岩石的可压缩程度，α=1 对应地层岩石完全不可压缩，R是表征地层流体量的数值，R=0 对应完全干燥地层），pf是孔隙流体压力。式中的参数α 和R可通过式（7）和式（8）从微观力学模型中计算得出

将式（7）代入式（6）可将R表达式变形为

式中，K，Ks，Kf，Ku分别表示排水孔隙弹性介质、固体颗粒、流体、流体不排水孔隙弹性介质的体积模量，φ为孔隙弹性介质的孔隙度。

在没有计算体积力作用的情况下，岩石和流体运动方程为

其中，ρf和ρ 是流体和孔隙弹性介质的密度，且ρ=(1-φ)ρs+φρf，ρs为固体颗粒的质量密度；qf为流体的流动单位向量；k为孔隙弹性介质的渗透率；η 为流体的黏度；a是表征流体附加质量的一个无量纲系数。

通过对物理量进行无量纲化，代入体积力方程，可以得到耦合后的岩石和流体的控制方程分别为

2.3 井周应力分布特征

与轴对称地层一般解的推导相似，可以对位移变量根据时间变量进行一系列的拉普拉斯–傅里叶转换[25]。拉普拉斯–傅里叶转换变换和逆变化公式为

其中，上标～表示拉普拉斯–傅里叶变换解，γ 足够大，即为大于f的关于s的所有奇点的实数部分。

由此，拉普拉斯–傅里叶变换中非对称平面应变变形的内部多孔弹性介质的一般解可以表示为

各项应力以及孔隙压力的拉普拉斯–傅立叶变换解为

其中，urn()，uθn()，wrn()，wθn() 为拉普拉斯–傅里叶变换后的地层固体和流体的径向、切向位移；σrn()，σθn()，σrθn()，pfn分别为拉普拉斯–傅里叶变换后的地层径向应力、切向应力、剪应力以及孔隙压力；Kn为第二类修正贝塞尔函数；An，Bn，Cn为由边界条件决定的常数，对于下标n，位移和应力的解中只存在n=0 和n=2 这两种情况，分别对应平均应力和偏应力作用结果，两者结合即为非均匀地层解，式中其他符号的替换方程为

令

2.4 破坏准则

通过模型得到地层的各应力分布后，为了直观地看出井壁稳定性的变化，本文通过摩尔–库伦破坏准则对模型进行转换，分析地层的坍塌趋势，建立了井壁失稳预测模型[26-27]。

摩尔–库伦破坏准则为

式中，τ和σ分别为岩石内部某一平面上的切向应力和垂向应力，S和φ是与岩石种类相关的物理量常数，φ表示岩石的内摩擦角，S表示岩石的聚合强度，也称为内聚力[28]。

摩尔–库伦准则在主应力空间的表现形式为

在孔隙弹性动力学模型中σ1和σ3表达式为

将主应力代入破坏准则，并定义M为坍塌指数，即

当M＞0，井壁围岩发生破坏，反之，井壁稳定。

2.5 模型参数设置

为比较分析模型结果，根据文章第1 部分室内单轴和三轴等实验结果，确定致密地层各项参数范围，然后计算模型所需的参数，并换算为无量纲参数，代入模型求出地层孔隙压力及各项应力的平面分布图解。

为方便后续对比，地层各项参数取值如表2所示。

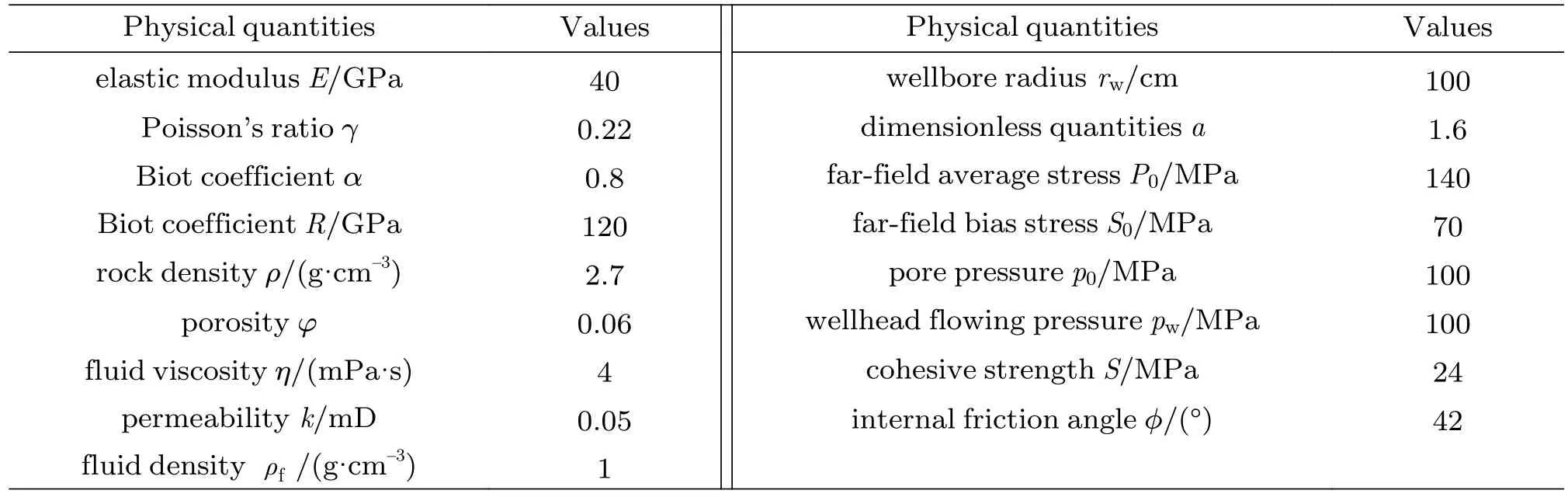
表2 地层各项参数取值Table 2 Values of various parameters of strata

根据地层参数值，对模型所需参数进行简单地计算。本文为研究岩石本征频率对模型坍塌指数的影响，引入饱和岩石本征频率的计算公式对其进行计算。

饱和岩石的本征频率为

式中，s是岩石迂曲度，可通过Yu 等[29]推导出的多孔介质迂曲度模型计算，模型中s仅与孔隙度φ有关，迂曲度计算模型为

由公式可知地层本征频率主要受两方面因素影响：①地层因素：孔隙度和渗透率；②流体因素：黏度和密度。其中本征频率与地层孔隙度、流体黏度成正比，与地层渗透率、流体密度成反比。本文所研究的深部致密地层属于低渗低孔隙度地层，其中地层因素较为稳定，地层孔隙度φ为5%～7%，地层渗透率k为0.1～0.01 mD，变化幅度小，地层流体密度也变化不大；而由于干湿气层或水层的矿化度不同等原因，会导致流体组分比例以及流体黏度发生变化，其中流体黏度变化较大，所以流体黏度的不同是岩石本征频率不同的主要影响因素。

拉梅常数λ 和剪切模量μ可通过公式由弹性模量E和泊松比γ 计算得出，即

模型所需参数如表3 所示。

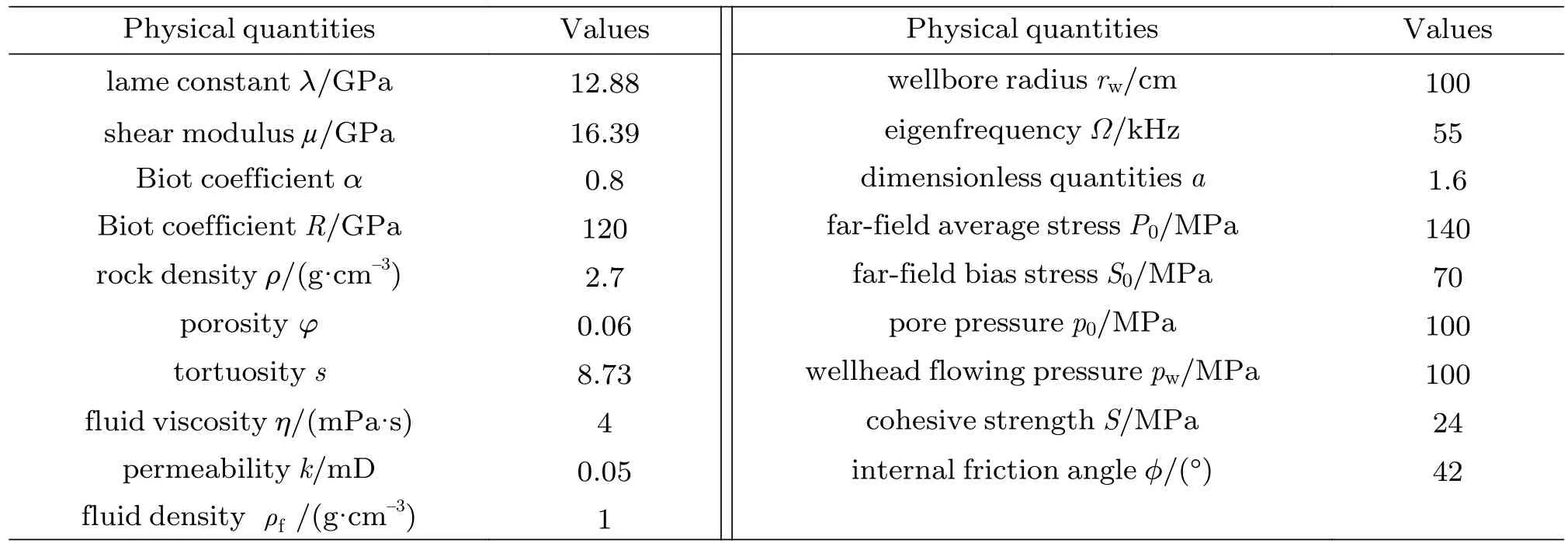
表3 模型所需参数取值Table 3 The values of the parameters required by the model

将表3 中参数依据式（15）中无量纲量的换算公式换算为模型所用无量纲数值，换算结果如表4。

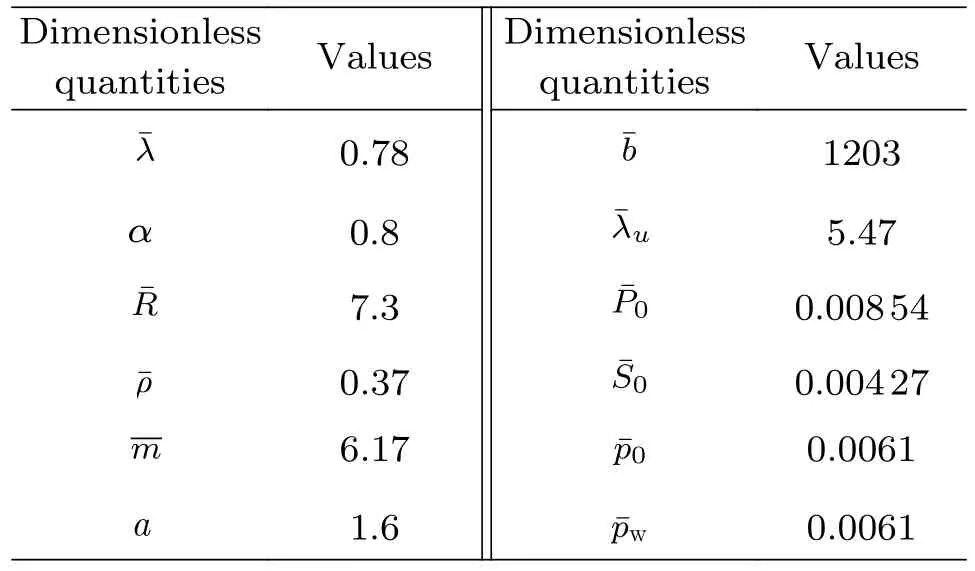
表4 模型所用无量纲参数值Table 4 The dimensionless parameter values used by the model

3 结果与讨论

3.1 本征频率的影响

图4 是在只改变岩石本征频率的情况下不同无因次时间的地层坍塌指数分布图[30]。由图可知，随着岩石本征频率的增加，地层坍塌趋势整体都呈现出上升趋势，地层也更易坍塌；随着无因次时间的增加，地层坍塌指数会先快速增加至一个峰值，再逐渐降低至一个不再变化的状态，相当于地层在打开之后其坍塌指数分布会发生一个较大的扰动。

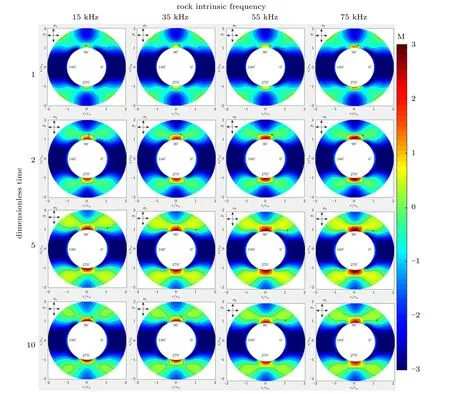
图4 岩石本征频率对坍塌指数影响Fig.4 Effect of rock intrinsic frequency on collapse index

图4 中，沿纵向排列的是时间变化对地层坍塌指数的影响。当本征频率维持不变时，地层高坍塌指数区域（沿最小主应力方向，井眼附近的两块月牙形红色区）的范围和大小随时间增加，先快速增长，再逐渐降低至不变。以未改变原始参数（Ω=55 kHz）情况为例，在=1 时刻，地层高坍塌指数区域刚刚发育成形，宽度只有0.15，坍塌指数也只有中心值部分达到了1，其他部分都在0～1 之间；=1 时刻到=5 时刻，是应力扰动导致井周稳定性越来越差的过程，在这一过程中，高坍塌指数区的范围迅速扩大，宽度变成0.3，区域内坍塌指数上升到2 以上，总体的增幅几近100%，到达地层最易破坏状态（峰值）；=5 之后，指数值逐渐降低，最终=10之后，地层坍塌指数分布不再变化，高坍塌指数区宽度恢复到0.2，区域内指数均值也降到了2（这一时刻后的状态与未考虑动力学效应的传统静力学模型相同）。由结果可知，在动态模型中，井眼打开之后，随着时间的推移，地层井壁稳定状态也有着动态的变化，且变化较大，传统模型未给出这一动态变化的过程，动态模型相较之能更好地反映地层失稳的本质。

图4 中，沿横向是本征频率变化对地层坍塌指数的影响。在一定的时间条件下，随着岩石本征频率的增加，井周高坍塌指数区域范围越来越大、中心值越来越高，地层也越容易失稳。以=5 时刻为例，在图中可以发现，岩石本征频率为15 kHz 时，高坍塌指数区域宽度为0.2，区域平均值为2；在岩石本征频率达到75 kHz 时，这一区域宽度达到0.，为Ω=15 kHz 时的2 倍，整个区域平均值达到了3。由此可见，岩石本征频率的变化对地层失稳有着较大影响。而对于传统模型预测结果，由于未对岩石本征频率的影响进行考虑，或只是单单考虑地层孔隙度、渗透率等的影响，本征频率从15 kHz 变化到75 kHz，高坍塌指数区域范围只增加了50%，均值几乎无变化。预测结果表明，在动力学范畴，除了一些地层的静态参数之外，地层应力波动频率与地层本征频率接近而导致的共振，也是特殊地层井壁坍塌问题所需考虑的重要影响因素。相比于传统模型而言，考虑到岩石本征频率影响的动力学模型在这方面得到的结果更加准确。

3.2 地应力的影响

图5 是固定岩石本征频率及其他变量，在最小水平地应力为100 MPa 的条件下，最大水平地应力分别取120 MPa，140 MPa，160 MPa，180 MPa 时，不同无因次时刻的地层坍塌指数分布图。由图可知，最大水平地应力增大，会使地层坍塌趋势大幅提升，地层失稳也更严重。

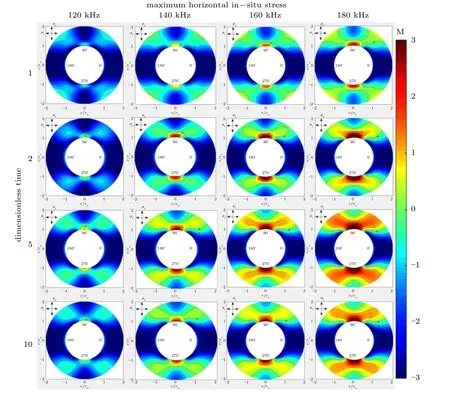
图5 最大水平地应力对坍塌指数影响Fig.5 Effect of maximum horizontal in-situ stress on collapse index

在最大水平地应力固定时，地层高坍塌指数区域的范围和大小随时间的变化规律与本文3.1 节所描述的相同，在此不再赘述。

在一定时间条件下，随着岩石最大水平地应力的增加，地层高坍塌指数区域范围越来越大、中心值越来越高，整体指数值也越来越大。以=5 时刻为例，在最大水平地应力为120 MPa 时，高坍塌指数区域宽度为0.，整体平均值为1；最大水平地应力为140 MPa 时，这一区域的宽度扩大到0.25；最大水平地应力达到180 MPa时，地应力增加了60 MPa，而这一区域宽度达到0.45，为最大水平地应力为120 MPa 时的3 倍，整体平均值也达到了3。以上分析可知，随着最大水平地应力的增大，每增大25%区域的面积都扩大了30%，整体的平均值也是成倍数增长。井周出现大面积的易失稳危险区域。结果表明，在该模型下，最大水平地应力的变化对地层整体的稳定性有着很大影响。在这一结果中，高坍塌指数区域的平均值和范围随最大水平地应力的变化都比传统模型的变化更大。因为在传统模型中，水平地应力的变化只作为改变地层应力状态分布的条件。而在高应力地层中，高的水平地应力会导致地层打开的动态瞬间应力平衡的破坏无法有效快速地恢复，这增加了地层失稳的可能性，而这一动态过程在动态模型中有所考虑，故模型中最大水平地应力对井壁稳定的影响也更大。