弹性模量的发现历程1)

张伟伟 马宏伟 武 静

(东莞理工学院机械工程学院，广东东莞 523808)

弹性模量也被称为杨氏模量，是固体力学中用于表征材料弹性变形的基本量，一般认为英国著名的博物学家、力学家托马斯·杨（Thomas Young,1773—1829）于1807 年首次提出了弹性模量的概念。其定义为在弹性范围内，应力σ与应变ε之比。不过，弹性模量的发现并非由托马斯·杨一人独立完成的。早在17 世纪末，雅各布·伯努利（Jacob Bernoulli，1655—1705）在研究梁的挠曲线时就涉及到了弹性模量。1696 年，欧拉利用变分法推导梁挠曲线时，认为梁弯矩与挠曲线曲率成正比，并将比例常数称为“绝对弹性”(absolute elasticity)。托马斯·杨于1807 年提出了弹性模量（the modulus of the elastic）的概念，并给出了“模重”和“模高”两类弹性指标描述材料的弹性模量。今天弹性模量的定义是纳维（Claude-Louis Navier，1785—1836）提出的。1826 年，纳维在分析梁变形及其强度时，区分了弹性模量（E）和截面惯性矩（I），从而将弹性模量从材料参数和结构参数的混合体中解放出来，使得弹性模量真正成为描述材料性能的力学指标。本文希望通过梳理弹性模量的发现历程，探索力学概念在其发展过程中的内在逻辑性。

1 托马斯·杨之前弹性模量的研究

众所周知，1676 年，胡克（Robert Hooke，1635—1703）给出了弹簧变形与力之间的关系，即胡克定律[1]

这里，F表示力，x表示弹簧变形量。k是表征弹簧弹性变形能力的常数，称为劲度系数或弹性系数。由式（1）可知，k可以通过力F与弹簧变形x的比值求得。胡克发现弹簧的弹性性质之后，就将这一性质推广到了固体材料中，他指出，具有弹性性质的各类构件都满足式（1）的公式。但胡克并没有对弹性模量这一概念进行深究，首先涉及到弹性模量的是瑞士数学力学家雅各布·伯努利（Jacob Bernoulli，1654—1705），他在讨论梁的弯曲变形中不自觉地用到了弹性模量。

17 世纪末期，莱布尼兹（Gottfried Wilhelm Leibnitz,1646—1716）提出微积分后迅速在欧洲大陆产生了广泛的影响，为了扩展微积分的应用范围，许多科学家提出各种各样的问题来扩展微积分的应用领域。雅各布·伯努利（Jacob Bernoulli，1654-1705）提出了一个微积分应用的力学问题，他很可能是第一位涉及到弹性模量的数学力学家。题目如下[2]：如图1(a)所示的悬臂梁，在其自由端作用一集中载荷P，求梁的挠曲线。

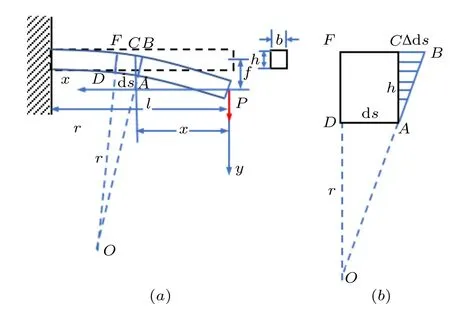
图1 雅各布·伯努利的梁弯曲变形

雅各布错误地以梁最下一层纤维变形作为梁的挠曲线进行求解，这来自于马略特对梁截面应力分布的一种误解。在雅各布之前的梁理论主要为伽利略（Galileo Galilei,1564—1642）和马略特（Edme Mariotte,1620—1684）梁理论，但他们主要研究了梁的强度理论。在讨论梁的破坏形式上，伽利略认为梁截面上的力是均匀分布的，说明伽利略对于梁的认识还没有中性层的概念，而马略特认为梁截面上的力沿着梁高度方向线性分布，他认为梁的最上面纤维所受的力最大，最下面一层纤维所受的力为0，相当于认为中性层位于梁的最下面一层[3]。雅各布采用了马略特的梁理论，他认为梁在变形中，最下面一层纤维保持不变，向上各层纤维的变形量线性增加，最上面一层纤维变形量最大，如图1(b)所示，设为[2]

雅各布认为每一层的变形量乘以弹性系数m，可得到每一层纤维的受力，这些力也沿梁高线性分布，这样可以求得梁截面上的合力为

雅各布认为截面上的合力的作用中心在距离梁最下面2h/3 处，因此，合力对截面最下面产生的弯矩等于外力P在该截面产生的力偶矩，因此有

假定梁在变形过程中，平截面假设成立，参考微段ACFD变形后变为ABFD，如图1(b)所示，显然，ΔBCA～ΔADO，因此有

将式（5）代入式（4），可得

现在，由《材料力学》知识可知[4-5]，梁弯曲时的曲率和弯矩满足关系

其中，I为截面惯性矩，对于矩形截面有I=bh3/12，将其代入式（7），得

比较式（6）和式（8）可知，m就相当于弹性模量，只不过雅各布以悬臂梁最下一层纤维为中性层，因此与弹性模量相差4 倍。雅各布也没有对弹性模量进行深入的讨论，他更关心梁的变形，得到了梁变形与弯矩之间的关系为：弯矩与梁变形曲线的曲率成正比。

1696 年，雅各布·伯努利的弟弟，约翰·伯努利（Johann Bernoulli，1667—1748）以公开信的方式，向全欧数学家提出了著名的“最速降线问题”，促成了一个新的学科-变分法的诞生。约翰的儿子，丹尼尔·伯努利（Daniel Bernoulli，1700—1782）建议欧拉（Leonhard Euler，1707—1783）（他是约翰的学生）采用变分法求解雅各布提出的梁变形问题，他在给欧拉的一封信里说道[2]：

由于欧拉没有考虑小变形，因此分母上的y′消不掉，致使方程（9）非常复杂。欧拉采用级数积分求解，得到当挠度很小的时候，C可通过式（10）求解

式中，yl是悬臂梁的最大挠度。如果考虑梁为小变形，忽略分子中的 3yl，可以得到梁的最大挠度为，《材料力学》教材[4-5]给出的结果为，可见欧拉的结果中，系数C就是抗弯刚度EI，欧拉把C称为“绝对弹性”，认为它是与材料的弹性性能以及梁截面形状有关的量。这里可以看出，当我们希望测试得到某种材料的弹性模量时，由于所制备的试样一定具有某种几何特征，如果不能剥离试样的几何特征，就永远不可能得到材料的弹性模量，这是提出弹性模量概念的主要困难。

除了研究梁变形中涉及到弹性模量外，在物体振动中，许多科学家也涉及到了弹性模量。1748 年，意大利科学家里卡蒂(Giordano Riccati,1709—1790)认为[6]：物体的弹性可以从它的振动频率推导出来。1782 年，他利用弯曲振动测定了钢相对于黄铜的弹性模量，这被认为是测定弹性模量的第一个实验，他得到的结果为[7-8]

相对弹性模量巧妙地避免了试样几何特征的影响，从而得到了材料的弹性属性。不过里卡蒂仍然没有给出弹性模量的概念，只是将其称为弹性性能（elasticities）。也有文献提到，欧拉在1727 年的一篇文章中，给出了应力与应变之间的线性关系[1]，其形式为σ=Eε，但缺少进一步的详细说明，仍需要做进一步的考证。

2 托马斯·杨的工作

托马斯·杨（Thomas Young，1773—1829）是英国著名的博物学家和科学家，21 岁就被选为皇家学会会员。他在光学（双缝干涉）、工程学（弹性模量）、生理学（视觉）、埃及学（破译罗塞塔石碑和象形文字）等多个领域做出了开创性的贡献，被当代英国传记作家安德鲁·罗宾逊（Andrew Robinson，1957—）称为世界上最后一个无所不知的人。1801 年，他被任命为皇家学院的自然哲学教授，1801—1802 两年时间内，杨共开设了91 场讲座，几乎涵盖了当时所有的已知学科，他的讲稿于1807 年被整理为《自然哲学和机械艺术讲座》（A Course of Lectures on Natural Philosophy and the Mechanical Arts），杨氏模量的提出也被包含在其中。他这样给出弹性模量的概念[9]：

“我们可以用同一物质的某一列的重量来表示任何物质的弹性，可以将其命名为其弹性模量(modulus of elasticity)，其重量是这样的，任何物质的增加都会使它以同样的比例增加，因为增加的重量会使相同直径的物质的一部分因压力而缩短。（We may express the elasticity of any substance by the weight of a certain column of the same substance,which may be denominated the modulus of its elasticity,and of which the weight is such,that any addition to it would increase it in the same proportion,as the weight added would shorten,by its pressure,a portion of the substance of equal diameter.）”

托马斯·杨提供了两种描述材料弹性模量的方法[10]。第一种描述是弹性模量的重量（the weight of modulus of elascity），假如有100 英寸长的杆被重1000 镑的重物压缩时缩短1 英寸，则称该杆弹性模量的重量为100 000 镑。如果用今天的语言来说，100 英寸的杆缩短1 英寸，相当于应变为0.01，如果1000 镑表示重力，可见模量的重量可由重力除以应变得到，即

在上述定义中，他所说的“某一列的重量”应该类似于如今我们称的材料中的“纤维”，这样就消除了利用压缩试样确定弹性模量时试样面积的影响。现在弹性模量的单位“帕斯卡”是1971年第14 届国际计量大会通过的，因此弹性模量的重量实际上并不是重量，它的单位是“镑/平方英寸”，这在英国工程师Thomas Tredgold（1788—1829）所著的A Practical Essay on the Strength of Cast Iron,etc中也可以看到。另一种描述为弹性模量的高度（the height of modulus of elasticity），并给出了一系列加载条件下的弹性模量高度的计算方法[11]。

可以看出，在应力、应变等基本概念还不十分清晰时，托马斯·杨定义的弹性模量在今天理解起来相当晦涩。正如另一位托马斯·杨的传记作者亚历克斯·伍德(Alex Wood,1879—1950)指出的那样：“这个定义是晦涩难懂的”。瑞利勋爵(Lord Rayleigh,1842—1919)是19 世纪物理学的巨人之一，他经常在他的科学论文中向杨致敬，同时也批评他的作品过于简洁而晦涩[9]。但托马斯·杨清晰地给出了弹性模量的概念，并指出这是一种不依赖于试样几何尺寸的固有性质，这与之前工程师们利用胡克定律把结构刚度与弹性模量混为一谈有着本质的区别，因此，人们也把弹性模量称为杨氏模量（Young’s modulus），以纪念他在物体弹性变形方面的贡献。此外，托马斯·杨还指出了这一模量既适用于棒的压缩也适用于杆的延伸，并且还适用于液体。他还特别强调了以下事实：胡克定律仅在物体保持弹性变形时适用，此后发生塑性变形就不再适用了。不过，我们今天所学的弹性模量的概念并不是托马斯·杨给出的，而是由法国力学家纳维（Claude-Louis Navier，1785—1836）于1826 年提出的。

3 纳维的工作

纳维完善弹性模量的概念，得益于19 世纪人们对应力、应变概念的认知成熟，以及材料测试实验力学的充分发展。早在1705 年，雅克布·伯努利给出了材料纤维在拉伸作用下的变形描述，即每单位面积上的力（应力）是每单位长度变形量（应变）的函数。欧拉于1752 年借用流体压强的概念来理解固体材料内部压力，法国数学家帕朗（Antoine Parent，1666—1716）于1713 年提出了剪应力的概念[1]。1822 年，柯西（Augustin Cauchy，1789—1857）在给法国科学院的一篇论文中首次以概括的形式提出了材料内部某一点的弹性条件，本质上就是应力和应变的关系。柯西认为，应力不仅可以用来预测材料的断裂强度，同时还可以用于描述固体内部任何一点的状态（一点处的应力状态），换句话说，固体中的“压力”很像液体或气体中的“压力”。它可以衡量构成材料的原子和分子在外力作用下被挤在一起或被拉开的程度[12]。柯西将一点处的应力属性由一组3×3 的数组组成，可转换为张量，并发展了各向同性固体的线弹性响应理论。作为他在这一领域工作的一部分，柯西还引入了用位移导数表示应变分量（3 个拉伸分量和3 个剪切分量）的几何方程，由此明确了应力和应变的概念。

在19 世纪的前几十年，大量的工程应用论文得到了广泛的传播。德国实验力学家Franz Joseph Ritter von Gerstner（1756—1832）设计出了可同时测定力与变形曲线的实验装置[13]，并对琴弦在受拉状态下的“力–变形”曲线进行了研究，如图2 所示（该图由Kurrer 依据Gerstner 的结果绘制），该结果说明Gerstner 测定的轧制钢的弹性模量为（换算为国际单位制）

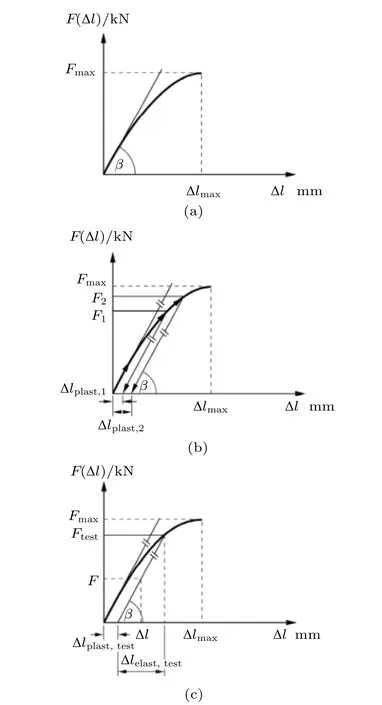
图2 铸铁拉伸时的力–变形曲线[14]

Gerstner 采用的单位为“Lower Austrian pounds per square inch”，换算成国际单位制，需要乘以系数0.0081，最终得到结果约为195 GPa，我们现在一般用210 GPa，大约小了7%。不过Gerstner 自己称弹性模量为弹性力比率（elastic force ratio）。

这一时期，人们对应力、应变的概念逐渐清晰，相关实验成果也日益丰富，即将揭开弹性模量的面纱，而完成这一工作的正是法国著名力学家纳维。1826 年，纳维在分析梁变形及其强度时，区分了弹性模量（E）和截面惯性矩（I），对于矩形截面梁给出了抗弯刚度（纳维用ε表示抗弯刚度）[15]

这里，纳维采用u,v表示x,y轴，b和c分别表示矩形梁截面的宽度和高度。式（12）所描述的结果就是现在材料力学中讲解的结果。其中，E为弹性模量，为矩形截面梁的截面惯性矩。要特别强调的是，纳维将弹性模量E视为物质常数，仅与材料有关而与结构的几何形状无关（几何部分用截面惯性矩来体现），同时纳维还给出了弹性模量的现代定义，即

在纳维的结构理论中，弹性模量占有极为重要的地位，可依据弹性模量来概括材料的力学性能实验。例如纳维改变了实验测试方案，经过大量的锻造铁实验，采用平均值作为材料的弹性模量，得到弹性模量为200 GPa 的结果。弹性模量终于走出了重重雾霾，在力学研究以及各种工程建设中发挥出重要作用。