WSN 中角度和距离结合的无信标节点定位算法的设计∗

张 拓，蒋 健，姚海峰，钱升港，毛科技，何文秀，赵永标∗

(1.浙江工业大学计算机科学与技术学院，浙江 杭州 310023；2.浙江省信息安全标准化技术委员会，浙江 杭州 310000；3.绍兴市越城区消防救援大队，浙江 绍兴 312000；4.浙江工业大学之江学院，浙江 绍兴 312030)

无线传感器网络(Wireless Sensor Networks，WSN)中节点的部署通常随机性较强且数量庞大，较难实现精准的节点定位[1]。然而在现实应用场景下，节点感知到的数据若缺失了位置信息，其利用价值会大幅降低。只有明确节点所在位置，才能将感知数据与位置信息关联，实现高效的感知[2]。因此，节点定位是无线传感网络的重要的支撑技术之一。由于节点所在位置的随机性以及其位置信息的重要性，实现节点的精准定位是无线传感器网络部署落地的关键。例如实际应用中节点需要通过飞行设备直接抛散在特定区域，其位置分布随机性较强且无法预先获取[3－4]。又如当节点部署的区域危险性较大，人类无法进入，或是敌对区域[5－6]。此外，在许多应用中，位置信息对传感器的监测工作非常重要，如火灾、地质勘测等等。因此，在现实场景中获取节点位置信息实现定位对WSN 具有重要意义[7－8]。

WSN 的定位方式可以分为有信标节点的定位方式和无信标节点的定位方式[9－10]。有信标节点的定位方式，即在WSN 中必须存在有一些节点通过某种方式，已经知道其具体坐标，例如利用全球定位系统。利用已知实际坐标位置的节点，其他节点就可以根据这些已知信标节点，进而估算出其他节点的坐标。无信标节点的定位方式，所得到的坐标系统可能仅为一相对于该WSN 之间的相对坐标系的位置与方位，然而这样的相对位置信息，足以吻合对象监测、同步、乃至信号传递等无线传感器的应用项目上，进一步，如果能够在这样的网络环境中获取到3组以上的真实坐标系中的位置信息，可轻易将该网络定位系统转换为实体坐标系统。

无信标节点的定位方式，在近几年逐渐受到重视，正如前所述，虽然由此算法所估测出的节点坐标并非处于绝对坐标系统之上，然而透过某些已知绝对位置的节点坐标，即可轻易将其转换为绝对坐标系统，即可大幅度提升在应用上的弹性。在以往所提出的有关于此类算法中，大多是以测量距离的方式，以进行定位的动作。虽然量测距离的装置成本较为低廉，然而由于量测装置本身的先天性因素，距离量测一般具有较大的测量误差，因此将影响到最后的定位结果。

因此，本文提出一种结合角度和距离测量的方法，在无需额外的信标节点存在之下，利用分布式定位方式，以逐步逼近式的方式来实现节点定位，同时对于同步中的节点进行比例式的调整，如此可缩小最后的定位误差范围，避免因少部分可能出现的较大测量误差而影响到整体的定位结果。实验结果表明，该方式在估算坐标误差上，可大幅优于其他同类型之不使用信标节点作为参考的定位方式。

1 相关研究

近几年以来陆续有人提出数种无信标节点定位算法，例如文献[11]提出的节点分布式定位算法，通过特定算法选取了5 个基准节点作为信标构建了一个新的坐标系，在新的坐标系中定位其他未知节点，在较低成本情况下实现了大规模的节点定位。文献[12]提出了一种虚拟信标节点定位算法，在普通节点中选取5 个虚拟信标构建坐标系，利用三边测量法进一步确定未知节点位置。文献[13]在聚类基础上提出一种无信标节点定位算法，该方法通过创建聚类，将节点的能量、连接程度以及三角不等式的几何极限定理这三个要素进行融合，减小了无信标定位中经常出现的累计误差，在能耗与定位精度上取得了较好的平衡。

文献[14]的定位方式是将所有的节点都利用监测其与周围节点的位置关系，分别建立出属于该节点的坐标系统。之后再结合每一个节点之坐标系统，逐步将所有节点的坐标系统合并，以建构一个总体之坐标系。还有很多相关的研究成果如文献[15－18]等。总的来讲，在以往所提出的有关于此类之算法中，大多是以测量距离的方式，以进行定位的动作。虽然测量距离的装置成本较为低廉，然而由于测量装置本身的先天性因素，距离测量一般具有较大的误差，因此影响到最后的定位精度。

2 算法设计

2.1 基本思想

本文提出一种结合角度以及距离量测的方式，在无信标节点存在之环境下，对无线传感器网络进行定位的算法。该定位方式可以将之区分为两个阶段:

第一个阶段在所需定位的WSN 中，确定某一些节点作为信标节点，并利用树的生成方式，分别以这些信标节点以作为树的起点，各自向周边延伸使节点之间以树状形态相互连结。

第二个阶段树的合并阶段，将所生成的树进行合并，以生成一个统一的树结构，在树的合并过程中，以树的高度为基础，当节点监测到其他非属于和自身同一树中的其他节点之时，则该两个节点在取得沟通之后，会根据所设定的加权值，决定两个节点之间的合并方向，直到所有的树都合并。

在角度同步当中，首先统一所有节点的坐标轴方位，然后利用坐标轴方位，以进行距离同步作业，最后决定节点之间的相对应位置。由于同时利用方位与距离检测，在节点定位时仅需检测到一个已知坐标节点，即可完成定位，有效增加可被定位节点比率，比聚类SPA 算法的定位精度要高。

2.2 算法实现

在进行算法同步作业前，首先将对节点进行树的形式建构，主要是增加同步的效率，使所有同步作业能够确保同步的效率，避免有绕远路径同步的情形产生。具体步骤如下:

2.2.1 信标节点的选择

待定位的WSN 系统中，为了要将节点之间以多个树状结构进行连结，首先选定数个节点作为信标节点，作为所生成树的树根节点。选择方式为监测网络中所有的节点，若该节点相对于周围的邻居节点，拥有较高的连结度，即将该节点选定为信标节点，如图1 所示。

图1 选定节点A 为信标节点

2.2.2 树的构建

选定了信标节点后，将以这些信标节点作为树的根节点，各自向外将其他的节点纳入，连结形成一棵树。树的产生方式由每个信标节点各自生成，当一个节点被纳入某一棵树中并成为其中的一个节点时，即成为该树的一部分，并以此节点继续扩展连结其他未被该树合并的节点，此树的扩展动作一直持续到没有其他的未被连结的节点存在于此树任何节点的监测范围。由于每棵树未必同时生成，因此最后所产生的每棵树的大小、节点数量未必一致，每棵树之间无需沟通协调，可节省能耗。

2.2.3 树的合并

若有一个节点中存在于多棵树的通讯范围以内，称该节点为“边界节点”，当两棵树要进行合并时，利用这些边界节点进行互相沟通。一棵树的合并扩展停止后，开始对其他树进行合并，每个边界节点，都试图去搜寻其他边界节点，当其搜寻到其他边界节点且又不属于同一树时，这两个节点会进行同步的准备动作，令此两节点分别为A与B。此两节点会根据其在该树中的高度值，以及其被该树合并至今所经历过的时间，演算出加权值，如式(1)所示:

式中:L(A)为节点A位于该树中的高度值，tNow与tA分别为合并请求的发生时间以及节点A初始生成的时间，α为预先估测之系数。W(A)为A节点此时所计算出之权重，加权值可模拟该树生成所经过的时间。两个节点之间会根据此加权值的大小以决定合并的方向，加权值较小的节点将会被加权值较大的节点合并后成为其子节点，同时也将脱离原先所隶属之树而加入较大加权值之树中。

2.2.4 方位的同步

假设在WSN 开始部署时，每个节点预先载入一个坐标轴系统，这样每个节点都拥有一个自识别的正北方向，该正北方向与实际之坐标系统存在有一偏差夹角，称之为“航位方向”。方位同步的目的，是采用渐进式逐步调整的方式，逐渐逼近所有节点之间的坐标轴方位，最终所有的节点都有一个统一的坐标系统与方位。然后该网络中任何节点取得了实际环境之坐标轴方位，即可调整航位方向，轻易地将坐标轴归正为实际坐标轴方位。

在方位同步的操作中，由每一个被推举出来的信标节点为起点，发起方位同步操作。若某一信标节点A拥有一子节点B，则该信标节点即可利用角度监测的方式，检测出子节点B其相对于该自身坐标的角度。同时，子节点B也得同时测量其与父节点A之间的相对角度。

如图2 所示，若存在有某一节点A为信标节点，节点A有一子节点B。若节点A监测到与节点B之相对方向角为θAB，而节点B监测得节点A之相对方向角为θBA，则父节点A的调整方式为式(2):

图2 节点A 与节点B 进行位置同步

式中:NA为节点A在进行方位调整前的方向角度，而－NA为同步时节点B调整的逆时针角度，θAB与θBA之范围为0～2π，分别为节点A所监测节点B相对于其所存在的方位角度以及节点B所监测出之节点A相对它的方位角度，其分别有一个可能的角度量测误差，分别为εAB与εBA，故经由节点所实际测量出来的角度量分别为εABθAB以及εBAθBA。SAB为该父节点同步操作下的调整比例，其值之设定为:

为节点A所拥有的子节点数量。同理，子节点B的调整方式为式(3):

此处的SBA＝1－SAB，其中，NB为方位调整前节点A的方向角度，而N′B－NB即为节点B在本次同步操作时所需调整的逆时针角度量，SBA为该子节点于此次同步操作下的调整比例，其值设定为:SBA＝1/(k×mi)，mi为父节点A所拥有的子节点数量，而k则为一常数值。

按这种方式，即可将节点A与B的方位角调整为图3 所示，在节点A获得定位结果之后，可继续向其子节点(如节点B)，进行同步操作，方向同步的操作是连续的，即同步动作会一直持续，直到定位完成为止。

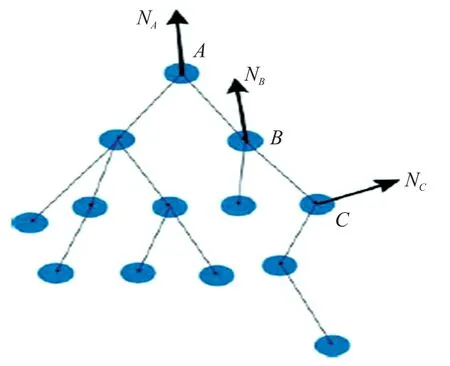
图3 节点A 与节点B 角同步

2.2.5 距离同步

在父节点A监测其某一子节点B之相对之存在方位之后，则该两个节点之间即可进行距离同步的测量与定位工作。距离同步无需和角度同步测量同时进行，即当节点A得知节点B之相对存在角度后，可将该相对方位信息储存于该节点内的数据结构中，然后可协助进行距离同步时协助节点进行定位。

距离调整比例设定:在距离的调整定位上，也采用同步的概念，渐进式地调整所有节点的相对坐标位置，假设有一父节点A以及其子节点B存在于某一树状结构当中，令A:(xA，yA)、B:(xB，yB)为该两节点在实际环境中坐标，而A′:(xA1，yA1)、B′:(xB1，yB1)则分别为该两节点的坐标，则在父节点A当中，定义:fA，B＝vA，B(dA，B－rA，B)，其中:vA，B为父节点A于先前处理方位同步时所测量出相对于节点B所形成的方向单位向量，为先前经由角度测量暂存在节点A中，dA，B为节点A与节点B之间的距离，根据两个节点个别的认知坐标所求出的距离值，故该值与实际该两个节点之间存在测量误差，即:dist(A，B)＋ε，其中ε为节点A测量其与子节点B之间的测量距离误差，rA，B为节点A所监测到之两点间之距离亦即为:dist(A，B)。

若节点A同时拥有数个子节点{B｜B∈child nodes ofA}，则父节点A利用上述方式，据以求出F＝∑(fA，B)。此F值即为该父节点相对于其各子节点之测量位置与原先估测距离的差距，由于考虑到避免一次完全的移动可能造成节点位置调整过于剧烈，因此以渐进式调整的方式，逐步调整节点的坐标位置。调整系数值k，配合该节点所拥有的子节点数mA，且令x′、y′ 分别为节点A原来自己的X轴与Y轴坐标，即得:

则:fAB＝(x″－x′，y″－y′)

则对于所有的子节点B:{B｜B∈child nodes ofA}，可以得到Total Force:F＝∑(fA，B)，根据此F向量值，可得出该次同步作业后节点A的坐标位置:

其中角度ϕ为F相对于WSN 由角度同步所形成坐标系统的方向角，mA为节点A所连结的子节点个数。则最后更新后的节点A坐标A′:(x‴，y‴)。而对于所有的子节点B，可以由其与父节点之同步过程当中所得:

式中:ε为父节点A所监测出节点A与节点B之间距离测量误差值，此ε值可调整比例值k一并由父节点A传给它。得到更新后的子节点坐标B′:(x‴，y‴)。在某一子节点完成该节点坐标位置更新后，该节点即可继续向其子节点进行坐标更新。

3 实验与分析

本文实验仅考虑在二维环境仿真，通过MATLAB实现仿真内容。仿真实验基于以下假设:

①在每次仿真前，根据参数(节点密度、距离测量误差、角度测量误差、通信半径)随机生成一个网络拓扑，节点的位置随机生成，服从随机分布；

②节点具备距离测量和角度测量能力，每次运行，所有的测试都随机运行30 次取均值，以选取较为平均的结果；

③节点收发消息正常，但是存在由MAC 层引起的消息冲突和消息重传，节点之间无障碍物，其通信模型采用自由空间电波传播模型，即各节点具有同样通信半径R，且通信范呈理想圆形，在此有效距离内，两个节点之间即可互相监测和通信。使用均匀的随机分布方式，所有的节点，随机分布于某一固定区域内。而每一个节点的有效监测范围为R，在此有效距离之内，两个节点之间可互相监测并通讯。

3.1 参数选择

首先假设一个450×450 的二维环境当中，以随机的方式均匀放置250 个传感器于其内，每一个节点的有效通信半径均为50。图4 为节点分布图，角度测量误差固定在正负五度的范围之内，距离测量误差则是以变动标准差的方式，其误差范围为0～8，分别皆以标准差的方式呈现。由于同步调整比例是以｜Ft｜/kmt的方式，动态调整父节点之同步比例，因此，在此实验当中，以不同的k值，有可能会分别找出其与测量误差之间的关系，比较不同的k值和最后定位结果的关系。节点部署完毕，首先是进入树的形成阶段。图5 为树形成阶段完成后树的分布仿真图。

图4 节点分布图

图5 节点树形成阶段分布图

树形成阶段过后便真正开始节点定位，先局部后全局，直到所有节点都获得一个全局坐标系中的唯一坐标值。首先分析不同的参数选择对定位误差率的影响，以便确定参数的选择。

3.2 距离测量误差与定位误差

首先，比较不同的距离测量误差与定位误差的关系。假设角度测量误差的标准差μ2固定在5%。距离测量误差则以变动标准差的方式，其误差范围为0～10。从图6 中可以得出:随着距离测量误差的增大，定位误差率也逐渐增大。变化不算明显，0～10 内都可以满足定位精度要求。

图6 定位误差率与测距误差率的关联

3.3 定位误差率的比较

对本方法的定位误差率进行实验，距离测量误差、角度测量误差以及算法计算误差是造成定位误差的主要因素。从图7 可得:①算法定位误差随节点节点密度增大而增加；②本方法相较于聚类SPA[19]在定位精度上有一定的提升。聚类SPA 算法与本方法对比精度提升更明显，坡度更陡。二者在节点密度为0.8 至1.0 之间曲线相交，之后本方法的定位误差率小于聚类SPA 算法，差距也慢慢明显。在节点密度较小的时候，聚类SPA 算法的定位误差率要小于本方法，主要原因是聚类SPA 算法定位节点少，且大部分围绕在中心树周边，产生的误差较小；随着节点密度的增加，本方法的定位误差率大幅度小于聚类SPA。

图7 不同节点密度时定位误差率比较

定位误差产生的主要原因包括距离测量和角度测量误差、坐标计算误差、节点节点坐标更新过程误差。定位误差率与节点密度呈正相关，主要是由同步阶段的误差累加。若要减小此类误差，通常需要减少更新迭代次数，即减少坐标节点数量计算的迭代次数，这正是本方法比聚类SPA 算法更有优势的地方，从而有效地降低定位误差率。

4 总结

节点定位技术是无线传感器网络中的研究热点之一，也是无线传感器网络实际应用中重要的支撑技术之一。大多数的定位算法都是依赖少数信标节点来确定其他多数一般节点的位置，而信标节点的坐标信息，基本上是由全球卫星定位系统来提供。这种借助信标节点来定位的方法至少存在以下问题:一是信标节点不可能很多，支撑数量较大的节点部署情况下的定位较为困难；二是信标节点由于人为或环境因素，常常出现位置漂移，造成其他节点难以精确定位；三是当环境位于室内或是具有某种干扰时，信标节点本身运作就会发生困难，当然其他节点也就难以定位。所以本文提出了一种角度和距离结合的无信标节点WSN 定位算法。在无信标结点存在的情况下，利用树结构分类及合并的思想，结合角度与距离的测量，进一步更新节点方位与坐标，从而实现节点在坐标系统中的精确定位。最后通过仿真实验表明，在节点随机分布并在一定的密度比例下，本文提出的算法在定位精度比聚类SPA 算法有明显的提高。