基于多特征融合与GSA-SVM 的滚动轴承故障诊断∗
2023-11-29李长杰谭玉涛
刘 杰,李长杰,赵 昕,谭玉涛
(沈阳工业大学机械工程学院,辽宁 沈阳 110870)
滚动轴承由于所处工作环境较为复杂,采集到的信号数据不仅包括了其相对应状态的特征,还包括了背景噪音等复杂环境噪声。在滚动轴承的故障诊断过程中,特征的提取与选择成为影响诊断准确率的重要指标。随着信息处理技术的发展,对滚动轴承的信号特征提取也从单一特征转换为多源域特征的提取。随着特征维度的增加,后续故障诊断的计算量也随冗余特征增加而增长。因此需要剔除无效特征和冗余特征,以此提升滚动轴承故障诊断准确率。特征融合是采用降维方法结合相关分析法对冗余特征进行筛选、剔除,降低特征维数,保留有效特征,降低后续诊断成本。
文武等[1]采用萤火虫算法改进信息增益的方法,将提取到的特征进行增益排序,并对排序后的特征进行最优子集筛选。范雪莉等[2]利用互信息计算变量之间的关联度,再结合所提的改进主成分分析方法,提取出主成分作为优化指标。姚登举等[3]采用随机森林并结合诊断准确率作为特征筛选融合的依据。欧阳武等[4]采用熵权模糊综合评价法构建多维专家偏好系数模型,实现主观和客观两方面评价水润滑尾轴承的优劣程度评估。齐咏生等[5]提出改进自适应变分模态分解法结合主成分分析(Principal Component Analysis,PCA)降维去噪构造故障诊断模型库,实现对监测信号的实时检测。Yang 等[6]通过多种聚类分析结合相关分析的方法实现对轴承数据特征的降维及故障分类。Wang等[7]提取故障诊断中常用指标如峭度、熵等的数学关系,并将相关指标通过计算平方包络权重得到标准化后的融合特征。Wei 等[8]提出了一种自适应特征筛选方法,通过所提方法实现对冗余特征的有效筛选,降低了故障诊断分类的计算成本。
本文通过提取时域、频域、能量及熵多维故障特征,实现对故障信号特征的充分表征。采用LLEEWM 对所提取信号进行多特征融合,筛选出有效特征集。最后采用GSA 改进SVM 的分类方法对融合特征集进行分类诊断,通过凯斯西储大学轴承数据集以及实测信号两类数据集的案例分析,验证本文方法的有效性及准确性。
1 振动信号的特征提取融合相关理论
1.1 时域及频域特征提取
由于时域分析的简单性和直接性,广泛地应用于各类滚动轴承在线检测系统之中。通过计算信号的简单统计特征来分析信号,然后选择适当的特征参数来准确地分类不同类型的故障,其中统计参数主要分为两类:有量纲特征、无量纲特征。如表1 所示,其中t1-t8为有量纲特征,t9-t14为无量纲特征。

表1 时域、频域特征及对应公式
对故障轴承的频域分析有助于监测其工作状态及发现振源的具体位置,故障在频域中会对应产生相应的故障分量。故障分量的振幅变化和是否有新的振动频率的生成,也是故障诊断过程中判断轴承的工作状态和劣化程度的依据。基于频域的分析方法可以平滑非平稳信号并反映信号中的特征信息[9]。本文所采用的频域特征包括重心频率、均方频率、均方根频率、频率方差、频率标准差、幅值谱和功率谱等。其中部分公式如表1 所示。
1.2 能量及熵特征提取
1.2.1 小波分解
对信号通过小波分解及不同频带的能量可以反映故障类型的深层信息。在小波分解过程中,会将信号分解为高频和低频两部分,其中低频系数之间的损失特征可以由高频表示出来。因此对信号高频部分的分解过程中不会产生遗漏特征的问题,也不会产生特征的冗余,可以实现信号的局部详尽分析[10]。对信号进行小波包分解:
式中:ε(t)为正交尺度函数;φ(t)为正交小波函数;h(n)和l(n)为滤波器系数。则小波包系数的递推公式为:
则得到重构公式为:
1.2.2 EEMD 分解
EEMD 集合经验模态分解是由经验模式分解(EMD)发展而来。EMD 是对时间序列信号进行分解得到多个相对简单的固有模态函数IMF 分量,由于其具有较强的自适应性,因此适用于对非线性非平稳信号的分析[11]。EEMD 则在EMD 的基础上避免了模式混合的问题,EEMD 的分解结果如式(4)所示:
式中:x(t)为原始信号;ui(t)为第i次实验分解得到的IMF 分量;r(t)为残差。
1.2.3 熵特征
信息熵是用来度量信号的不确定性和复杂程度的特征,即给定变量a,a可能出现的值a∈{a1,a2,…,an},和每个值出现的概率σ,σ∈{σ1,σ2,…,σn}且=1,则变量a所包含的信息熵为:
信息熵描述的是信号的复杂程度,当复杂程度高,其值就越大。当变量对应的概率值σ相等时,信息熵达到最大[12]。
模糊熵是当时间序列变化时,生成新的故障类型的可能性概率,其值随着序列复杂度的升高而增加[13]。模糊熵的表达式如下式所示:
当N的长度有限时,代入式中可得:
式中:m为嵌入维数参数;n为边界梯度;r为相似容忍限度。
1.3 LLE 降维与熵权评估
局部线性嵌入算法是对每个数据点度量与其临近点的局部关系,并对临近点计算重构权重,以此实现最大程度低维表示[14]。具体计算过程如下:
①对样本点的邻近局部关系线性重构并计算权重:
式中:n为样本总数;样本x(i)的邻近样本量为ι;为样本x(i)与邻近样本之间的权重系数;wi,j为样本与第j个邻近样本之间的权重系数。
②保持样本点的邻近局部关系,进行降维:
式中:Z为维度低于原始特征的降维后特征;z(i)为第i个样本降维后的特征。
熵权法是一种较为客观的计算权重的方法,其值越大说明该数据中所包含的信息越多,具体步骤为:
①确定评价对象,构造评价矩阵(Rij)mn,i=1,…,m;j=1,…,n,其中m为评价对象个数,n为评价指标个数;
②标准化评价矩阵:
③计算对应熵值:
1.4 GSA 改进SVM 原理
支持向量机通过将样本投射至高维空间中,在高维空间中采用最佳决策边界分离数据的间距,从而找到分离数据类型的最佳超平面[15]。解决非线性情况下的公式为:
式中:ω为超平面权重向量;ξi为松弛变量;xi为需分类样本;yi为样本对应类别;b为训练阈值;C为惩罚函数。惩罚函数是对错分样本的惩罚率,它用于最大化分类范围和最小化误分类样本数折衷,是一个对SVM 分类性能有重要影响的参数。
通过引入拉格朗日函数和核函数来解决式(10)中凸二次规划问题,并对ω、b求偏导并将偏导数等于0,得到如下公式:
式中:αi为拉格朗日算子;kernal(xi,xj)为核函数,本文选用径向基函数作为核函数,其优点是泛化性能良好,其表达式如下:
式中:支持向量机的分类能力受到C、g参数的影响。且SVM 本自身的C、g取值常需要依赖经验法设定,因此本文引入引力搜索算法对SVM 中的C、g两个参数进行寻优。
引力搜索算法是一种基于牛顿引力定律和粒子间相互作用的智能优化算法[16]。首先设定参数C、g的搜索范围及粒子种群大小,设置GSA 随机搜索初始位置,通过对粒子位置及运动速度迭代,在达到最大迭代次数时,输出最佳C、g参数值。
本文所采用的基于LLE-EWM 结合GSA-SVM的故障诊断流程如图1 所示。

图1 多特征融合故障诊断流程图
2 凯斯西储大学轴承实验案例分析
2.1 数据描述
采用凯斯西储大学轴承实验数据[17]验证所提特征融合方法的有效性,其中试验台由三相异步电动机、扭矩编码器、振动加速度传感器等部分组成,如图2 所示。

图2 凯斯西储大学试验台图示
试验中所采用的SKF6205 型号轴承,根据不同的故障深度将故障分为轻度故障,中度故障和重度故障,共10 类轴承运行状态。每类样本采集到120 000 个数据点,取1 200 为故障的一个样本,每类故障得到100 个样本。具体参数如表2 所示。
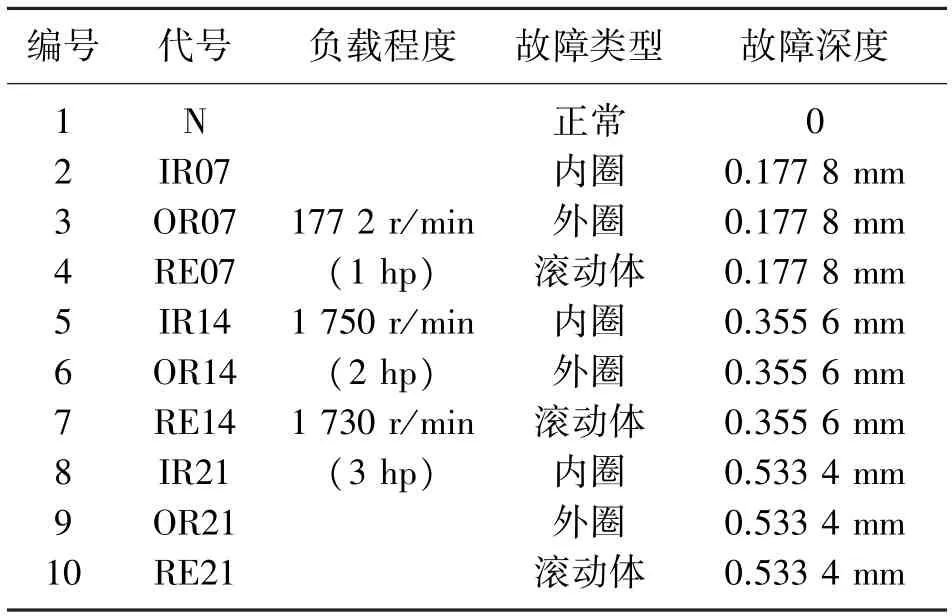
表2 凯斯西储大学轴承数据具体参数
其中以负载条件3 hp,故障深度为0.533 4 mm及正常运行状态下的的轴承振动信号为例,轴承振动信号的振动特征如图3 所示。
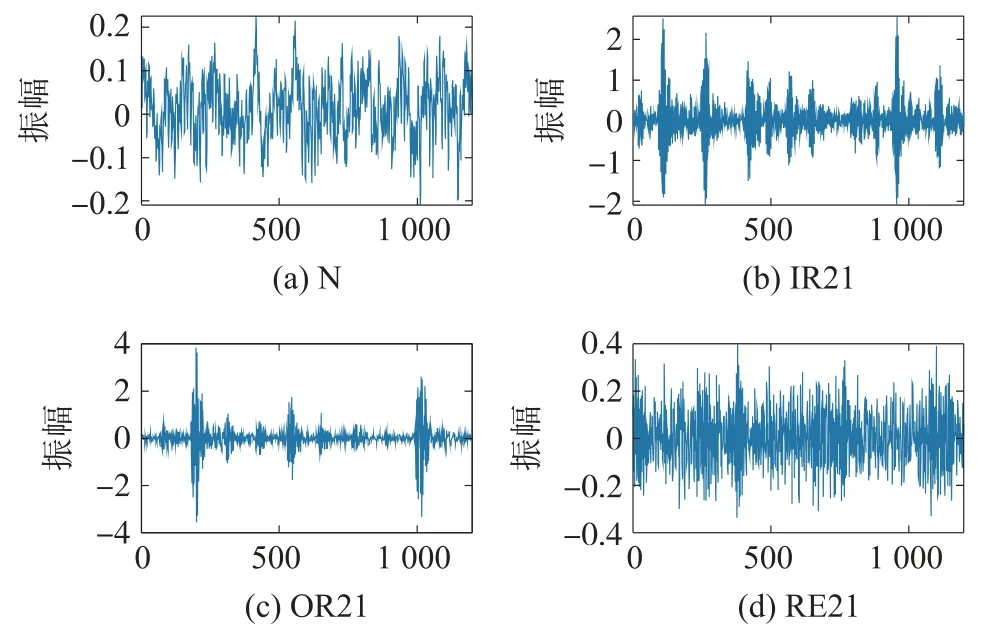
图3 滚动轴承故障深度0.533 4 mm 振动信号
2.2 滚动轴承多源域特征提取
首先对滚动轴承原始信号进行第一节所提到的时域、频域、能量及熵特征的提取,并设置时域特征为T=[t1,t2,…,t14],频域特征为P=[p1,p2,…,p7]。其中能量特征包含小波分解的6 维特征,EEMD 分解得到的14 个IMF 特征,构成的能量特征为E=[e1,e2,e3,…,e19,e20]。熵特征由信息熵和模糊熵构成χ=[χ1,χ2,χ3,χ4,χ5,χ6,χ7]。得到含有48个特征的滚动轴承特征数据集Q1。每类故障特征选出一个绘制特征图示,如图4 所示。

图4 多源域提取特征图示
2.3 多源域的特征筛选及融合
提取到的48 个信号特征会导致诊断过程中的计算量过大,从而降低对滚动轴承的诊断效率。首先采用SVM 对48 类信号特征进行第一轮的筛选。通过对单一特征进行诊断得到相应的诊断准确率,如图5 所示。

图5 48 个特征筛选
由图5 所示,其中柱状图高度为单特征由SVM诊断的准确率,其中1~14 代表时域特征;15~21 代表频域特征;22~41 代表能量特征;42~48 代表熵特征。以阈值50%为例,保留大于50%的特征为有效特征。50%阈值筛选得到有效特征为38 个,60%阈值筛选得到有效特征为28 个。
计算筛选得到的特征之间的皮尔逊相关系数,得到相关系数最大的特征,如表3 所示。

表3 阈值50%筛选最大相关系数及对应特征
由表3 可得,通过计算38 个筛选特征和对应特征的相关系数,得到38×38 的系数矩阵,筛选得到每个特征对应的相关性最大特征。筛选后得到时域特征8 个;频域特征1 个;能量特征10 个;熵特征1 个。
对剩余的时域特征和能量特征采用LLE-EWM方法进行处理。采用LLE 算法对时域特征和能量特征进行降维处理,设置算法临近点数为20,维数为2,得到7 维敏感特征及对应的权重,分别为:0.181 0、0.135 6、0.161 8、0.117 0、0.158 6、0.099 4、0.146 6。采用相同方法对阈值60%特征进行计算,如表4 所示。

表4 阈值60%筛选最大相关系数及对应特征
经过相关系数筛选后得到:时域特征7 个、频域特征1 个、能量特征7 个、熵特征1 个。采用LLEEWM 计算主成分及权重,得到7 维敏感特征及对应的权重,分别为:0.126 9、0.122 3、0.171 8、0.118 1、0.197 4、0.144 5、0.119 0。图6 为筛选后的7 个特征权重图示。
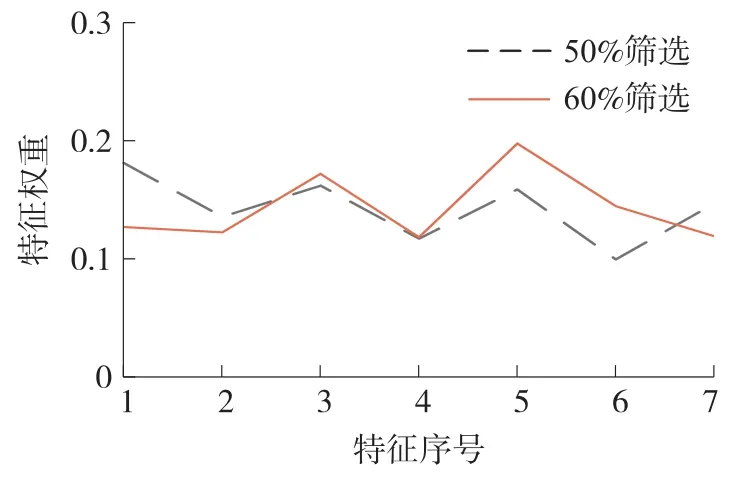
图6 筛选特征的权重
2.4 基于GSA-SVM 多特征融合故障诊断
将50%及60%筛选后的特征数据集输入GSASVM 分类模型中,在模型训练之前对信号特征进行归一化,并将计算得到的特征对应权重与归一化的特征相乘。将处理过的特征输入模型,得到GSA 对SVM 的寻优曲线及诊断结果。将50%准确率筛选的轴承故障信号特征,按照70%训练、30%测试的比例输入GSA-SVM 中,通过GSA 对SVM 进行参数寻优。迭代过程及诊断结果如图7 所示。
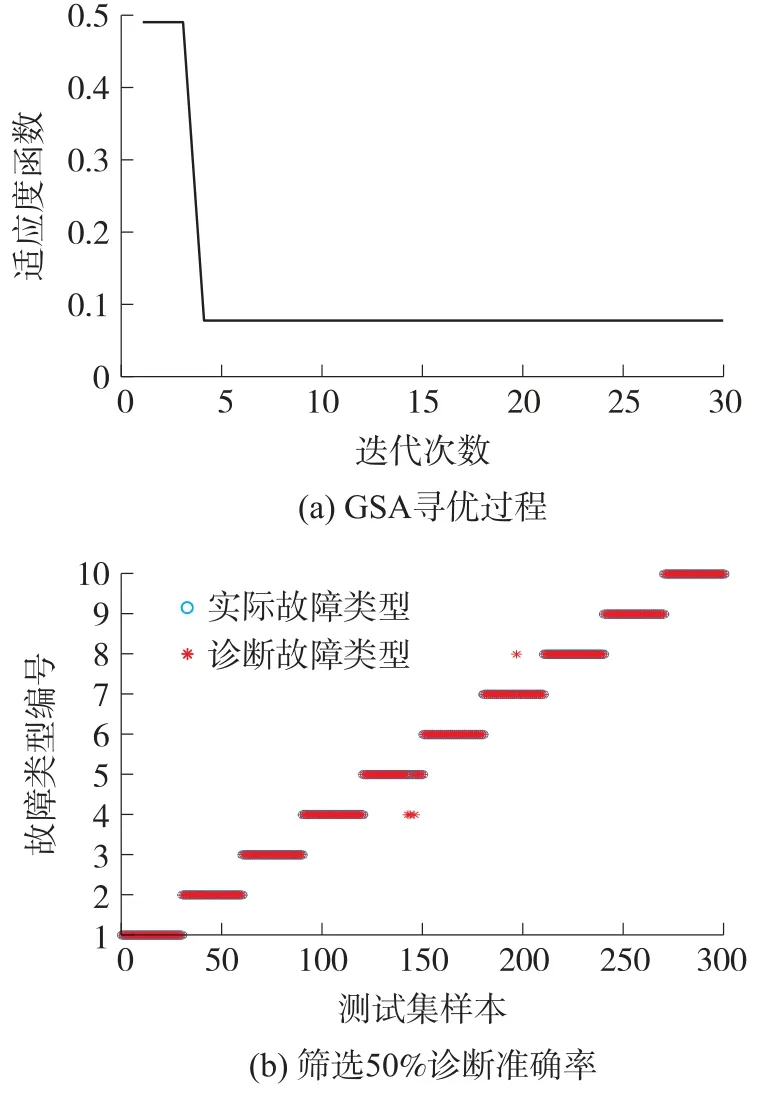
图7 融合特征集诊断结果(50%准确率)
经过30 次迭代后得到最终的诊断结果为98.7%,相较于单一故障的故障诊断,所提多故障特征融合方法的诊断结果具有更高的准确率。
将60%准确率筛选的轴承故障信号特征,按照与上文相同的划分方法输入SVM 模型进行寻优。迭代过程及诊断结果如图8 所示。

图8 融合特征集诊断结果(60%准确率)
经过30 次迭代后得到最终的诊断结果为99.7%,相较于按照50%划分的故障诊断结果,60%划分方法的特征具有更高的诊断精度,说明相对较高的筛选要求能够有效地提升诊断准确率和效率。
3 对比实验
为了验证GSA-SVM 对滚动轴承故障诊断的能力,将所提方法与GridSearch-SVM、PSO-SVM 以及GA-SVM 对50%和60%阈值融合特征进行故障诊断。通过不同的模型对SVM 的寻优对比,验证本文所提方法的诊断精度,同时验证不同筛选比例对诊断结果的影响。得到相应的对比结果如表5 所示。
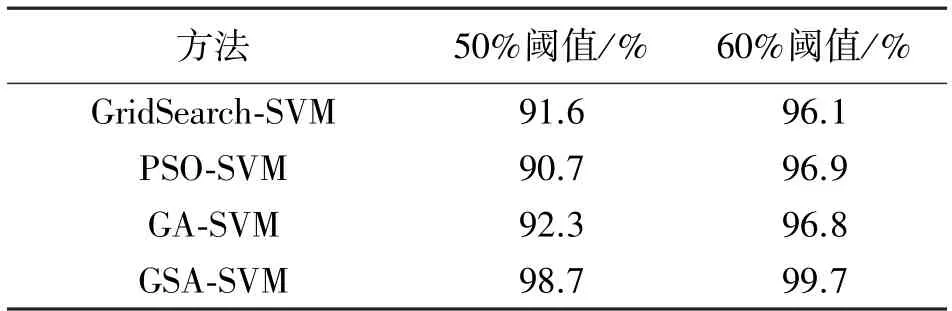
表5 不同方法诊断结果
表5 所示的结果表明,在阈值的选择过程中,选择50%阈值融合特征在不同寻优模型的诊断准确率,均明显低于60%阈值特征融合。同时对比其他方法,本文所提方法在不同条件下的故障诊断结果均可获得更高的滚动轴承故障诊断精度。
4 结论
本文提出了一种基于LLE-EWM 的滚动轴承多特征融合方法并结合GSA-SVM 实现轴承的故障诊断。通过实例验证,可以得出以下结论:
①提取滚动轴承48 维特征信号集,并结合皮尔逊相关分析以及LLE-EWM 进行故障特征的融合。从而实现对故障信号所包含的信息进行综合提取。
②对多特征融合的故障特征输入GSA-SVM 模型中进行诊断,通过设定不同筛选阈值以及对比不同的SVM 寻优模型。实现特征融合的阈值选择,验证了所提方法具有较高的故障诊断精度。
结果表明所提方法具有较高的故障诊断能力,能够较为充分地提取出故障信号中所包含的特征信息,在故障诊断过程中也能较为准确地诊断出滚动轴承的故障种类及程度。
