一种基于EWT-ICEEMDAN 的单通道脑电信号眼电伪迹去除算法∗

宋 婷，舒智林，孙玉波，韩建达，于宁波∗

(1.南开大学人工智能学院，天津 300350；2.南开大学天津市智能机器人技术重点实验室，天津 300350)

脑电图(Electroencephalogram，EEG)是大脑神经细胞群活动在大脑皮层的综合反映，是头皮表面记录到的大脑神经元产生的电活动，用于量化大脑电活动状态，广泛应用于脑机接口和疾病诊断等[1－4]。随着技术的发展，脑电信号采集设备更加便携，通道数目也在不断减少，甚至为单通道，研究单通道脑电信号伪迹去除算法对于准确有效地分析大脑活动是至关重要的[5－6]。

在脑电信号采集过程中，位于额叶区域的脑电通道极易受到眼电伪迹(Electrooculogram，EOG)的干扰[7－8]。眼电信号的幅值远高于脑电信号，且频谱与脑电信号的δ频段重叠[9]。针对上述问题，研究者们已经提出了从脑电信号中去除眼电伪迹的各种方法，包括回归方法、盲源分离(Blind Source Separation，BSS)、小波变换(Wavelet Transform，WT)和经验模态分解(Empirical Mode Decomposition，EMD)等[10－11]。回归方法是单通道脑电信号中去除眼电伪迹最直接的方法，需要同时采集脑电和眼电信号，增加了硬件复杂度，且存在脑电和眼电双向污染的问题[12]。盲源分离是将不同来源的多通道信号分解为多个独立分量，去除伪迹相关的独立分量。该算法对于多通道脑电信号具有较好的效果，但由于其要求通道的数量必须大于等于源的数量，所以对于单通道脑电信号并不适用[13]。小波变换是脑电信号中伪迹分离的重要方法，但是存在母波选择、分解层数设置以及在频谱重叠情况下去噪效果不佳的问题[14－15]。经验模态分解是将脑电信号分解为有限个不同时间尺度的本征模态函数(Instrinsic Mode Functions，IMFs)，去除以眼电伪迹成分为主的IMFs。该算法可以在无任何先验知识的情况下对信号进行自适应分解，对于脑电等非平稳信号的处理具有突出优势，但是对噪声比较敏感，容易造成模态混叠的问题[16]。

针对单一方法的优缺点，研究人员开发了结合两种或多种方法的算法。Maddirala 等[17]将奇异谱分析(Singular Spectrum Analysis，SSA)得到的参考信号用于眼电伪迹的自适应噪声去除(Adaptive Noise Cancellation，ANC)，用于解决单通道脑电信号眼电伪迹去除问题。该算法存在模态混叠及嵌入维度等参数选择的问题。罗志增等[18]提出了一种将自适应完备经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN) 和独立成分分析 (Independent Component Analysis，ICA)相结合的算法，用于单通道脑电信号中眼电伪迹的去除。虽然CEEMDAN 将单通道信号分解为多维数据，满足了BSS 的先验条件，但是脑电和眼电信号存在频谱混叠，会将脑电和眼电信号分解到同一个IMF，直接去除IMF 会导致脑电信号失真。张锐等[19]结合小波变换和集合经验模态分解(Ensemble EMD，EEMD)两种方法自动去除单通道脑电信号中的眼电伪迹。虽然算法复杂度低，但是没有给出含眼电伪迹的小波成分选择标准，且EEMD 算法会存在噪声残留的问题。

为此，本文针对脑电信号和眼电伪迹存在频谱混叠的问题，创新性地提出一种单通道脑电信号中眼电伪迹自动去除算法。采用经验小波变换(Empirical Wavelet Transform，EWT)[20]将单通道脑电信号分解为δ频段和高频段信号，采用改进的自适应噪声完备经验模态分解(Improved CEEMDAN，ICEEMDAN)[21]将得到的δ频段脑电信号分解为多维本征模态函数IMFs，设置样本熵阈值自动去除以眼电伪迹成分为主的IMFs，最后重构得到滤波后的脑电信号，使用半模拟脑电数据和真实的脑电数据对算法进行验证，并与其他方法对比。

1 方法

本文提出的单通道脑电信号眼电伪迹去除算法EWT-ICEEMDAN 的流程如图1 所示。该算法首先采用EWT 算法将含眼电伪迹的单通道脑电信号分解为δ频段和高频段信号，然后采用ICEEMDAN 算法将δ频段信号分解为有限个IMFs，进一步设置样本熵阈值去除含眼电伪迹的IMFs，最后重构得到去除眼电伪迹的单通道脑电信号。

图1 单通道脑电信号眼电伪迹去除算法流程图

1.1 基于经验小波变换的脑电信号分解

EWT 通过生成自适应滤波器组来提取输入非平稳信号的模态分量，不仅能克服EMD 噪声残留的问题，还能根据信号频谱的不同调整滤波器组的带宽，克服离散小波变换(Discrete Wavelet Transform，DWT)分解信号滤波器组恒定的问题[20]。研究显示眼电伪迹主要影响脑电信号的δ频段，当脑电信号中存在眼电伪迹时，δ频段的功率谱密度较高[17]。因此，本文采用EWT 提取脑电信号的δ频段和高频段信号。EWT 分解过程如下:

首先，对于给定信号f(t)通过傅里叶变换得到傅里叶频谱，假设将傅里叶支撑区间[0，π]分割成N个连续的区间，各个区间可表示为Λn＝[ωn－1，ωn]，其中，n＝1，2，…，N，并且满足＝[0，π]。以ωn为中心，定义过渡相Tn＝2τn，其中，τn＝γωn(0<γ<1)，γ满足式(1):

式中:β(x)的表达式为[22]:

最后，得到近似小波系数Wf(0，t)和细节小波系数Wf(n，t)，公式如下:

原始信号f(t)可被重构为:

EWT 通过对信号频谱进行显著的分割来创建自适应滤波器组，然后将单通道脑电信号的傅里叶频谱分割为δ频段和高频段，对应的频率范围分别为[0，4]Hz 和[4，40]Hz，最后得到δ频段信号fδ(t)和高频段信号fhigh(t)。

1.2 基于ICEEMDAN 的δ 频段脑电信号分解

ICEEMDAN 不仅能解决模态混叠的问题，还能解决CEEMDAN 中的残留噪声和伪模态问题[21]。本文采用ICEEMDAN 对δ频段的脑电信号fδ(t)进行分解。设Ek(•)为EMD 分解得到第k个IMF 分量的算子，w(t)(i)为服从N(0，1)的白噪声。ICEEMAN 算法的流程如图2 所示，对于δ频段的脑电信号分解过程如下:

图2 基于EMD 的ICEEMDAN 分解IMF迭代流程示意图

①在信号fδ(t)中添加噪声构成信号fδ(t)(i)＝fδ(t)＋ε0E1(w(t)(i))，i＝1，…，N。对每个fδ(t)(i)进行EMD 分解得到第一个余量信号:

②计算第一个IMF:

③在第一个余量信号中添加噪声构成信号r1(t)(i)＝r1(t)＋ε1E2[w(t)(i)]，估计第二个余量信号，得到第二个IMF:

④对于k＝3，…，K，在第k－1 个余量信号中添加噪声构成信号rk－1(t)(i)＝rk－1(t)＋εk－1Ek[w(t)(i)]，计算第k个余量信号:

⑤计算第k个IMF:

⑥重复步骤④～⑤，直到所获取的余量信号是一个单调函数或常量时，分解过程停止。此时，δ频段的脑电信号fδ(t)最终被分解为:

式中:εk－1为第k次分解中添加噪声的系数，通常取值范围为[0.1，0.3]。

1.3 基于样本熵的眼电分量识别

样本熵是一种衡量时间序列复杂度的方法[23－25]。脑电信号中包含大量的信息，复杂度高，样本熵值较高；而眼电信号频率低，复杂度低，样本熵值较低。本文通过设置样本熵阈值可实现脑电分量与眼电分量的判别。样本熵通常表示为SampEn(m，r，N)，其中m表示嵌入维数，r表示相似容限，N表示数据长度，其可以定义为:

式中:Am(r)和Bm(r)分别表示预处理后的信号与根据嵌入维度n＋1 和n构造成的新序列在相似容限r下匹配的概率。本文选取r＝0.2std[x(i)]，(std[x(i)]表示时间序列x(i)的标准差)，m＝2。

计算得到各个IMF 分量的样本熵值之后，需要设置阈值才能区分脑电和眼电伪迹成分。图3 所示为半模拟数据集中54 组FP1 通道纯净脑电信号及眼电信号的样本熵分布情况。从图中可以发现，纯净脑电信号的样本熵均在0.4 以上，因此将样本熵阈值设置为0.4，可以区分脑电分量和眼电分量。

图3 纯净脑电信号与眼电信号的样本熵分布曲线

2 试验

2.1 数据获取

为了验证本文提出的EWT-ICEEMDAN 算法的有效性，分别使用半模拟的脑电数据和真实脑电数据进行了评估。

半模拟数据集使用的是Klados 和Bamidis 于2016 年公开发表的数据集[26]。该数据集记录了27名健康受试者在闭眼期间的脑电数据，包括14 名男性(平均年龄:28.2±7.5 岁)和13 名女性(平均年龄:27.1±5.2 岁)。脑电电极按照国际标准10－20系统在头皮上放置，信号的采样频率为200 Hz，经过0.5 Hz～40 Hz 的带通滤波和50 Hz 的陷波滤波。本文做单通道脑电信号的眼电伪迹去除，选取距离眼睛最近受眼电影响较大的电极Fp1 进行眼电伪迹去除。从这27 例受试者中，总共采集54 组脑电数据，采集到的脑电数据不含眼电伪迹，可以作为纯净的脑电信号。此外，记录受试者在睁眼期间的眼电信号，分别为垂直眼电(Vertical EOG，VEOG)和水平眼电(Horizontal EOG，HEOG)信号，采样频率同样为200 Hz，经过0.5 Hz～5 Hz 的带通滤波。根据式(21)生成含眼电伪迹的半模拟脑电信号[27]。

式中:Scon表示含眼电伪迹的脑电信号，SEEG表示纯净的脑电信号，SVEOG和SHEOG分别表示垂直和水平眼电信号，a和b分别表示垂直和水平眼电的污染系数。

真实数据集采集12 名受试者(10 名男性，2 名女性，平均年龄:24.1±1.1 岁)在睁眼情况下FP1 电极的脑电信号，采样频率为2 000 Hz，降采样到200 Hz，再经过0.5 Hz～40 Hz 的带通滤波和50 Hz的陷波滤波，从每名受试者的数据中选取10 段含眼电伪迹的脑电信号，每段数据段长度为10 s，共得到120 段数据。

2.2 效果评价

在本文中分别从时域和频域两方面对EWTICEEMDAN 算法的性能进行评估。在时域方面，计算纯净的脑电信号SEEG和去除眼电伪迹后的脑电信号Sclean之间的相关系数(Correlation Coefficient，CC)和相对均方根误差(Relative Root-Mean-Squared Error，RRMSE)[28]。CC 的定义为:

RRMSE 的定义为:

式中:Cov(•)表示协方差，Var(•)表示方差，RMS(•)表示均方根。

相关系数评估两个信号之间的相关性，CC 值越大，表示二者的相关性越大，即去除眼电伪迹后的脑电信号信息保留越完整，失真越小。相对均方根误差评估信号的幅度失真情况，RRMSE 值越小，表示眼电伪迹去除越完全，与纯净的脑电信号越接近。

在频域方面，使用两个脑电信号质量指标来评估所提出算法的性能，分别为含眼电伪迹的脑电信号Scon和去除眼电伪迹后的脑电信号Sclean在δ频段能量比(Energy Ratio，ER)的变化以及在δ、θ、α、β频段的功率谱(Power Spectral Density，PSD)的平均绝对误差(Mean Absolute Error，MAE)[29]。Scon在δ频段的ER 定义为:

同样，Sclean在δ频段的ER 定义为:

进一步，计算含眼电伪迹的脑电信号Scon和去除眼电伪迹后的脑电信号Sclean在各个频段的功率谱的平均绝对误差，以α频段为例，的定义为:

对于真实的脑电信号，无法提取纯净的脑电信号，因此不能使用时域指标CC 和RRMSE 对眼电伪迹去除效果进行评价。在频域方面，计算眼电伪迹去除前后脑电信号在δ频段能量比的变化ΔERδ以及在各个频段的功率谱的平均绝对误差

为了进一步验证本文算法的有效性，本文对比了DWT、文献[19]提出的WT-EEMD 以及文献[29]提出的FBSE-EWT-LPATV 算法。所有的对比实验包括:

①DWT 算法:首先使用基函数将脑电信号分解成L 级系数，然后将高于阈值的每一级的系数设为零，最后用逆DWT 重构脑电信号。在文献[14]中研究了四个基函数:haar、coif3、sym3 和bior4.4 以及通用阈值和统计阈值。作者认为，基于统计阈值的bior4.4 基函数是去除眼电伪迹的最佳选择。

②WT-EEMD 算法:采用EEMD 算法将含眼电伪迹的小波成分分解为若干IMFs，通过设置自相关系数阈值去除含眼电伪迹的IMFs，最后重构得到去除眼电伪迹后的脑电信号[19]。

③FBSE-EWT-LPATV 算法:在文献[29]中首先基于傅里叶－贝塞尔级数展开的经验小波变换(Fourier-Bessel Series Expansion based Empirical Wavelet Transform，FBSE-EWT)将脑电信号分为δ频段，再基于局部多项式逼近的全变分算法(Local Polynomial Approximation based Total Variation，LPATV)去除δ频段的眼电伪迹，最后与其他频段信号线性重构得到去除眼电伪迹的脑电信号[29]。

3 结果和讨论

3.1 半模拟数据测试结果

在本文中，对半模拟数据使用本文算法进行眼电伪迹去除处理，并与DWT、WT-EEMD 和FBSEEWT-LPATV 三种算法进行对比。

图4 分别显示了含有眼电伪迹的脑电信号以及使用EWT 提取得到的δ频段和高频段信号。在δ频段信号中，眼电伪迹清晰可见。随后，采用ICEEMDAN 算法对δ频段脑电信号进行分解。图5所示为δ频段脑电信号经过ICEEMDAN 分解后的IMFs 结果及其对应的样本熵值。可以发现IMF4～IMF10 的样本熵值小于0.4，即为眼电伪迹，去除相应的IMF。最后重构得到去除眼电伪迹后的脑电信号，如图6 所示。

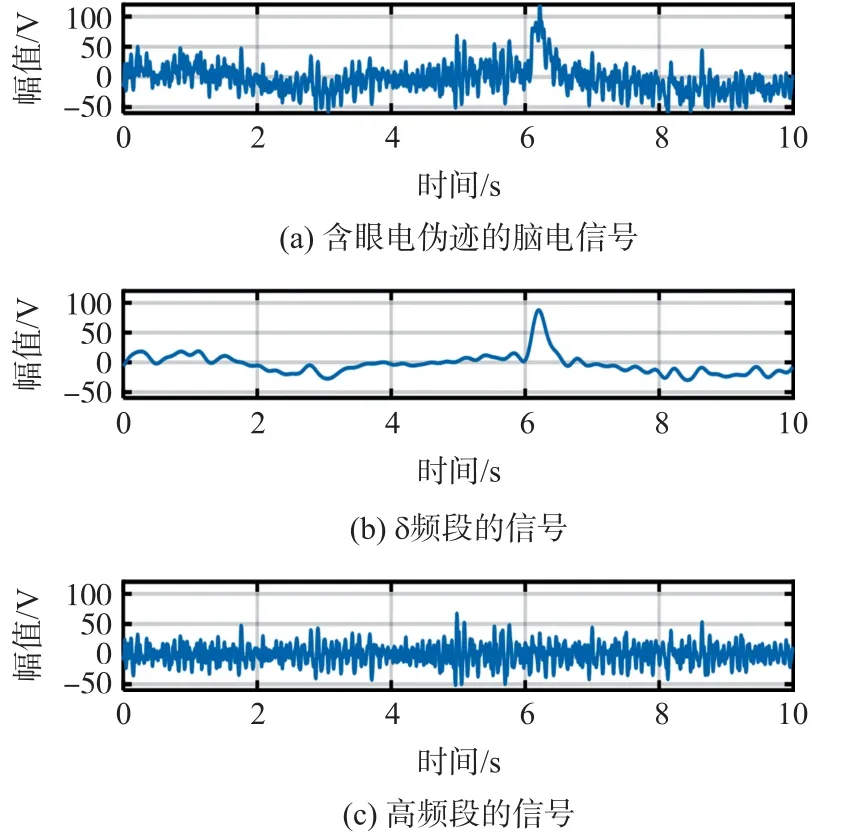
图4 含眼电伪迹的脑电信号及δ 频段和高频段信号

图5 δ 频段信号进行ICEEMDAN 得到IMFs 分量

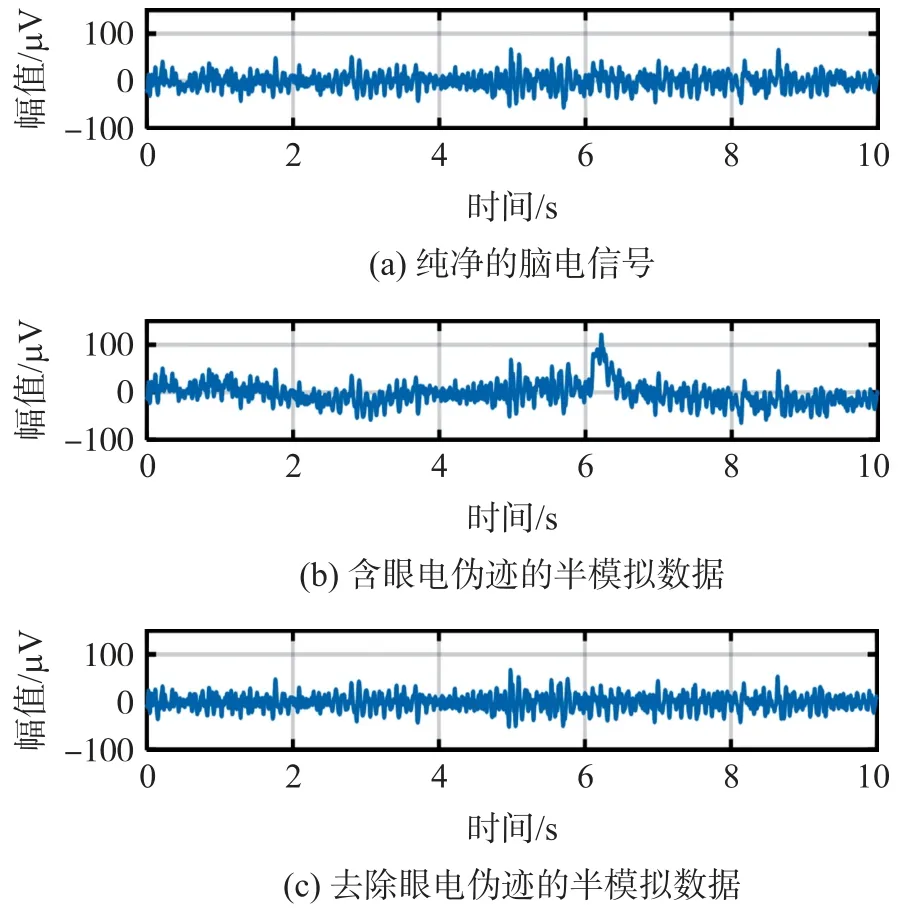
图6 本文算法对半模拟数据中眼电伪迹去除

在时域方面，计算纯净的脑电信号和去除眼电伪迹的脑电信号的CC 和RRMSE 的均值及标准差，评估不同算法对于相同脑电信号的眼电去除效果及算法的稳定性。表1 所示为本文算法、DWT 和WTEEMD 三种算法的CC 和RRMSE 结果对比。CC 值越大，表示眼电伪迹被去除的同时，脑电信号失真越小。可以看出，本文算法的CC 均值高于其他两种算法。RRMSE 值越小，表示眼电伪迹去除的越完全。本文算法的RRMSE 均值和标准差均低于另外两种算法。因此，本文算法去除眼电伪迹的同时，信号失真最小。在频域方面，计算眼电伪迹去除前后的脑电信号的ΔERδ以及在δ，θ，α，β频段的MAE均值及标准差，并与文献[29]中所提出的FBSEEWT-LPATV 算法结果对比，如表1 所示。可以看出，本文算法ΔERδ的均值在50%以上，说明该算法具有较好的去噪效果。对比四种算法，本文所提出的算法在θ，α，β频段功率谱的MAE 均值基本小于其他算法。因此，去除眼电伪迹后的脑电信号中保留了θ，α，β频段的信息。

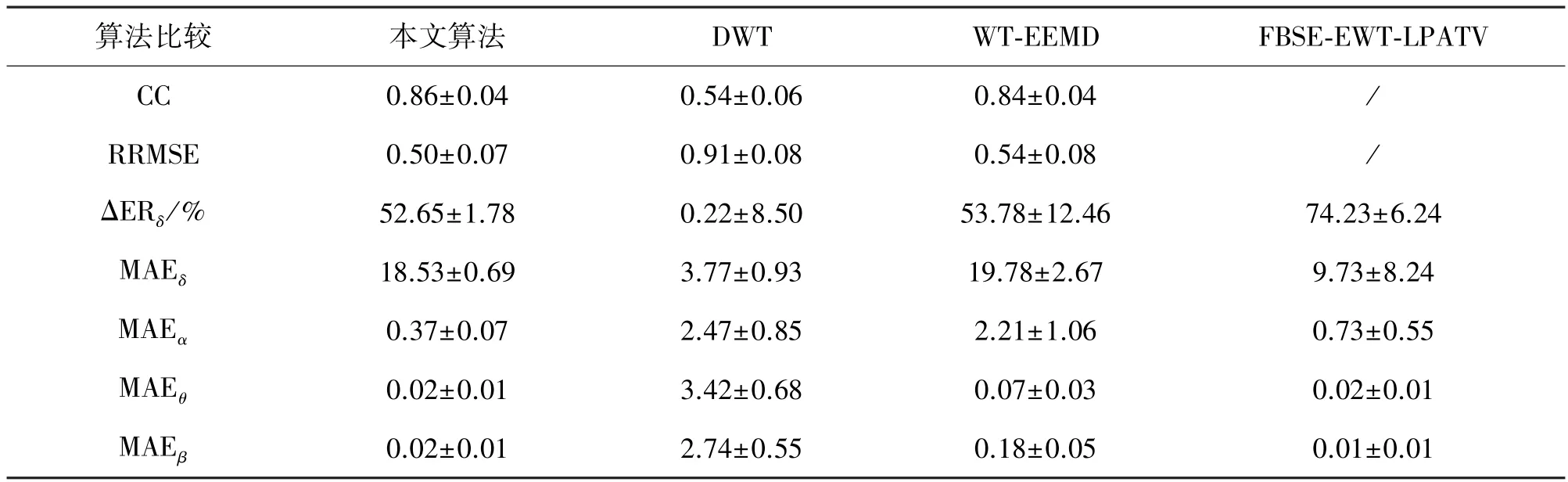
表1 四种算法的眼电伪迹去除效果评价结果(均值±标准差)

3.2 真实数据测试结果

图7 所示为本文算法、DWT 和WT-EEMD 三种算法对同一段真实脑电信号处理前后的时域波形对比。可以看出，本文算法在去除眼电伪迹后，在原眼电伪迹位置处不存在眼电波动，WT-EEMD 算法处理后存在较少波动，而DWT 算法处理后剩余较多波动。

图7 三种算法对同一段真实脑电数据的眼电伪迹去除效果

在本文中，对每名受试者的10 段含眼电伪迹的脑电数据都使用本文算法、WT-EEMD 和DWT 算法进行眼电伪迹去除处理，并计算δ，θ，α，β频段功率谱的平均绝对误差的均值及标准差，用于评价眼电伪迹去除算法对真实脑电数据进行处理的脑电数据失真情况。表2 为本文算法、WT-EEMD 和DWT 算法去除眼电伪迹后的δ频段的ΔERδ以及在δ，θ，α，β频段的功率失真情况。很明显，所有真实脑电信号的ΔERδ均值为71.20%。同样，θ，α，β频段功率谱的MAE 均值分别为0.52、0.07 和0.07。可以看出，本文算法在θ，α，β频段的失真情况均小于WTEEMD 和DWT 算法，且标准差最小，说明该算法对去除脑电信号中的眼电伪迹是有效的。

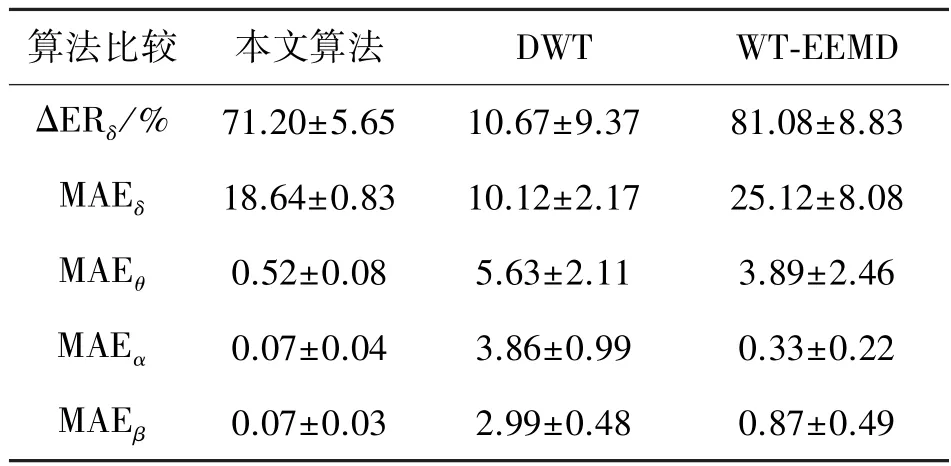
表2 三种算法的眼电伪迹去除效果评价结果(均值±标准差)

4 结论与展望

针对已有眼电伪迹去除算法存在脑电信息丢失的问题，本文提出一种基于经验小波变换－改进的自适应噪声完备经验模态分解算法(EWT-ICEEMDAN)，利用样本熵判别脑电和眼电分量，进行单通道脑电信号眼电伪迹去除。通过半模拟的脑电信号和真实脑电数据进行实验验证，相比于DWT、WTEEMD 和FBSE-EWT-LPATV 三种算法，本文提出的单通道脑电信号中眼电伪迹去除算法的效果更优，既能去除眼电伪迹，又能最大程度地保留脑电信息。在未来工作中，我们将考虑更多能够有效区分脑电分量和眼电分量的判别依据如模糊熵[18]，并且我们将进一步研究能够满足实时性的方法。