单端初级电感变换器的分数阶建模与仿真分析
2023-11-29谢玲玲蒙远杰
谢玲玲,蒙远杰
(广西大学 电气工程学院,广西 南宁 530004)
分数阶微积分是整数阶微积分的扩展,随着自然界中物体分数阶微积分特性的发现,利用分数阶微积分描述复杂系统越来越受到科研人员的关注。
近年的研究表明,实际的电感和电容具有分数阶微积分的特性,本质是属于分数阶的,用分数阶微积分理论对其进行描述更为准确。电感和电容作为DC-DC变换器主要组成部分,将分数阶微积分理论应用于变换器的建模,可以得到更准确灵活的分数阶模型。文献[1]分析了分数阶微积分不同定义的特点,搭建了R-L分数阶定义下buck变换器分数阶建模。在该分数阶定义下,分数阶阶数会对变换器的电压增益、电感电流、以及静态工作点产生影响;文献[2,3]以boost变换器作为研究对象,对电流连续模式和电流断续模式下的分数阶模型进行了研究,推导了电流连续和断续的条件,表明电感和电容阶数会对系统的工作状态造成影响,并且通过仿真试验验证了正确性;文献[4]以分数阶boost变换器为控制对象,采用分数阶PID进行控制,实现了全分数阶闭环控制,试验结果表明分数阶闭环系统具有更好的性能;文献[5]采用等效小参量法和状态空间平均法,推导了Buck-Boost变换器的分数阶模型,得到了分数阶阶数对状态变量谐波特性的影响规律;文献[6]对断续模式下buck-boost变换器的分数阶建模问题进行了研究;文献[7]基于Caputo分数阶微积分的定义建立了反激变换器分数阶模型,推导了分数阶互感的等效电路模型,分析了分数阶阶数对系统传递函数和输出的影响。目前对DC-DC变换器分数阶建模的研究,主要集中在Buck、Boost、Buck-Boost、flyback等低阶变换器,而对SEPIC、Cuk、Zeta等高阶变换器的分数阶建模的研究较少。单端初级电感变换器(Single ended primary inductor converter,SEPIC)可以实现升压和降压,且存在输出与输入电压同相、输出纹波小、效率高等优点,广泛应用于电动汽车供电系统[8,9]、光伏发电系统[10,11],建立更准确的分数阶模型,可以为变换器参数设计和闭环系统优化提供更多的选择。
本文以SEPIC作为研究对象,推导了变换器的分数阶数学模型,搭建了电路模型并与整数阶模型进行对比研究。
1 分数阶微积分与Oustaloup算法
1.1 Caputo分数阶微积分的定义
分数阶微积分理论在数百年的发展过程中,形成了几种公认的定义:Cauchy积分公式、G-L定义、R-L定义及Caputo定义[12]等。在这几种分数阶微积分定义中,Caputo定义对常数的微分等于零,和整数阶微分对常数的微分结果相同,对于解决实际工程中的零初值问题比较适用;R-L定义考虑了分数阶微积分对常数导数不为零的情况,用于建模虽然相对更准确,但模型的复杂度会大大增加,且提升程度比较有限,对于高阶的SEPIC变换器而言,不是非常适用。
(1)
Caputo分数阶微分定义为
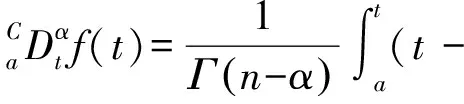
(2)

当变量处于零初始状态时,其分数阶微分的拉普拉斯变换可以表示为
(3)
1.2 Oustaloup算法
Oustaloup算法[13]是一种有理逼近算法,在指定的频率范围内,可以有效地对分数阶微分算子sα的幅频特性和相频特性进行拟合,是实现微积分算子的重要方法之一。Oustaloup算法的计算公式如下
(4)

2 SEPIC变换器分数阶数学模型
分数阶电感、分数阶电容的数学模型[4]与整数阶类似,都是表征它们电流和电压的关系,不同的是它们的关系以分数阶微积分进行表示,表达式如下
(5)
式中:α表示分数阶电感的阶数,β表示分数阶电容的阶数,取值范围为[0,1]。


图1 分数阶SEPIC变换器拓扑结构图
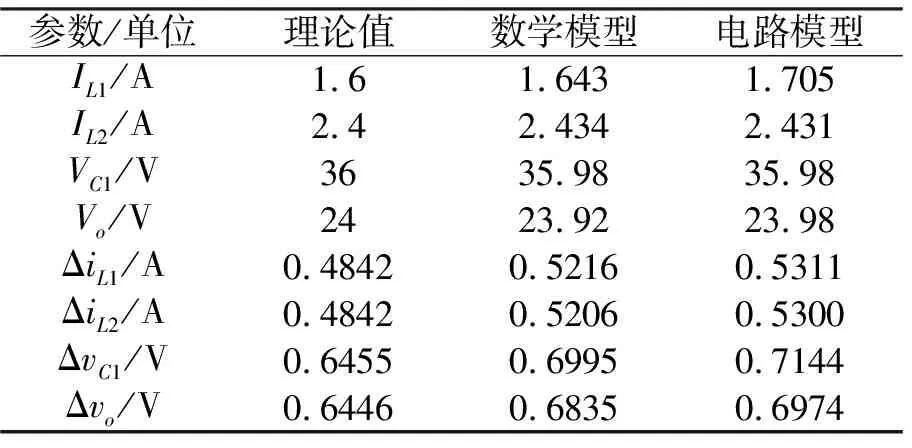
工作模态1(0 (6) 工作模态2(dt (7) 状态空间平均法[14]是DC-DC变换器常用的建模方法,其主要原理是在一个开关周期内对系统的变量求平均。根据分数阶微积分理论,分数阶微积分和整数阶微积分具有相似的运算规则,因此状态空间平均法同样适用于分数阶变换器的建模。对分数阶SEPIC的变量求平均值后,可以得到分数阶状态平均模型 (8) 式中:〈iL1〉、〈iL2〉、〈vC1〉、〈vo〉和〈vg〉分别为对应变量的开关周期平均值,d是开关管的占空比,d′=1-d。对开关周期平均变量进行分解,得到不变的直流部分以及小信号扰动部分,分解结果如下 (9) (10) 式(10)忽略高阶小量并化简后,分解得到的直流分量表达式 (11) 式中:D′=1-D。由Caputo分数阶微分的定义可知,常数的分数阶微分等于零,式(11)等号左边变为0,化简后得到变换器的静态工作点的表达式 (12) 结合式(6)和式(12)进行计算,得到分数阶电感L1和L2在(0,dT)区间内的电流纹波ΔiL1和ΔiL2,进行化简之后,得到它们的纹波的表达式 (13) 又有VC1=Vg,故当取L=L1=L2、α=α1=α2时,可以统一表示为 (14) 式(14)表明,电感L1和L2在满足数值大小和阶数相同的条件时,纹波的大小也将相同,且电感的阶数α会影响电流纹波ΔiL的幅值。利用MATLAB软件绘制得到电流纹波ΔiL随阶数α变化的曲线,如图2所示。可以得出如下的结果:阶数α的减少,会导致电感电流纹波ΔiL急剧增大,0.7阶时的纹波幅值远远大于1阶时的纹波幅值,阶数降低容易使变换器进入电流断续运行模式。 图2 电感电流纹波与电感阶数的关系 根据式(6)和式(12),还可以得到分数阶电容C1和C2在电压纹波ΔvC1和Δvo计算公式,化简之后表示如下 (15) 式中:Eβ(·)为Mittag-Leffler函数[2]。从式(15)可以看出,电容电压纹波大小也与它的阶数有关,二者关系如图3所示。由图3可知,电容C1和C2的阶数为0.75至1阶时,两者电压纹波幅值基本相同,阶数小于0.75阶时才开始出现比较明显的区别。此外,与电感电流随阶数变化的结果相似,电容电压纹波也是随着电容阶数的减少而急剧增大的。因此,当实际电感和电容阶数较低时,采用整数阶模型得出的结果是不够准确的,此时应该考虑使用分数阶模型进行分析。 图3 电容电压纹波与电容阶数的关系 式(10)忽略高阶小量和化简后,得到交流小信号部分表达式为 (16) 将式(16)进行分数阶拉普拉斯变换,结果如下所示 (17) 对频域下的分数阶微分方程组式(17)求解,得到输入到输出、占空比到输出的分数阶传递函数Gog(s)和God(s) (18) (19) 式中: b0=(VC1+Vo)D′ b1=-DL1(IL1+IL2) b21=L2C1(VC1+Vo)D′ b11=L1C1(VC1+Vo)D′ b3=-(IL1+IL2)L1L2C1 a0=D′2 a1=(L1D2)/R a2=(L2D′2)/R a11=L1C1D′2 a12=L1C2D2 a21=L2C1D′2 a22=L2C2D′2 a3=L1L2C1/R a4=L1L2C1C2 对式(18)和式(19)进行分析可知,输入到输出、控制到输出分数阶传递函数与电感、电容的分数阶阶数均有关系。电感和电容分数阶阶数的改变,会导致系统的传递函数发生变化,也意味着变换器的动态特性的改变。当α1=α2=β1=β2=1时,分数阶模型的传递函数与计算得出的整数阶模型相同。 根据Oustaloup算法,可以得到SEPIC的分数阶数学模型,如图4所示。 图4 SEPIC变换器分数阶数学模型 Fractional Int s^{-0.9}为分数阶积分算子,是将Oustaloup算法计算的传递函数,在Simulink下进行子系统封装后得到的,其内部结构如图5所示。Oustaloup算法存在拟合频率和拟合阶数的选择问题,拟合频率的范围越大,拟合阶数越高,对各种频率信号的响应越准确。当选择拟合频率为ωb=1×10-4rad/s、ωh=1×107rad/s,阶数N=10时,具有比较高的拟合精度,也不会导致电路实现困难。 分数阶电感和分数阶电容是通过分抗电路进行等效实现的,其结构如图6和图7所示。将变换器拓扑中的整数阶电感和电容分别用等效电路进行替换,构成SEPIC的分数阶电路模型,如图8所示。 图5 分数阶微分算子结构 图6 分数阶电感等效电路模型 图7 分数阶电容等效电路模型 图8 分数阶SEPIC电路模型 在频域下,分数阶电感和电容可表示为:Lsα,1/Cs-β,本质是分数阶微积分算子乘上一个系数,基于Oustaloup算法得到拟合传递函数并进行部分分式分解,与分抗电路传递函数比较即可获得相应电路元件参数。当分数阶电感和电容的阶数均取0.9阶时,可得分抗电路元件的参数如表1所示。 在MATLAB/Simulink仿真平台搭建分数阶数学模型与电路模型,将电路模型的开关管S和二极管D设为理想元件进行仿真,得到仿真结果如图9所示。由式(12)~(14)计算出分数阶SEPIC变换器静态工作点和纹波的理论值,与图9所得到的试验结果进行比较,绘制在表2上。由图9和表2可以看出:分数阶数学模型与电路模型所得结果误差极小,基本一致;仿真结果与理论值虽然存在一定的误差,但误差也比较小,考虑到计算与仿真过程存在近似环节,这样的误差是可以接受的。经过对仿真结果的分析,验证了SEPIC分数阶模型的正确性。 表1 α1=α2=β1=β2=0.9时分抗电路参数 表2 分数阶数学模型与电路模型仿真结果对比 根据对小信号传递函数的分析,分数阶模型受到电感和电容分数阶阶数的影响,动态特性随着阶数发生变化。为了验证理论分析的准确性以及研究分数阶阶数对变换器的影响,将分数阶积分模块用Simulink软件给出的整数阶积分模块进行替换,得到整数阶数学模型,如图10所示。在相同条件下进行仿真,仿真结果如图11所示。 由图11测得整数阶模型的试验数据:IL1=1.607 A,IL2=2.409 A,VC1=35.99 V,Vo=23.99 V,ΔiL1=0.144 0 A,ΔiL1=0.144 0 A,ΔvC1=0.192 0 V,Δvo=0.192 0 V。由此可知,分数阶模型静态工作点与整数阶模型基本相同,但分数阶模型稳态时纹波则远大于整数阶模型。从两个模型的输出响应曲线可以看出,分数阶模型输出电压的响应速度更快,超调量更小,达到稳态的时间更短,具有更好的动态响应性能。 图10 SEPIC整数阶数学模型 图11 整数阶模型与分数阶模型仿真结果对比 本文基于电感和电容属于分数阶的事实,采用状态空间平均建模方法和分数阶微积分理论,推导了SEPIC的静态工作点、电感电流纹波、电容电压纹波和分数阶小信号传递函数,搭建了SEPIC的分数阶数学模型、分数阶电路模型和整数阶模型,对比分析了不同模型的仿真结果,得出了以下的结论: (1)电感和电容的分数阶阶数,对变换器的静态工作点基本没有影响,但会影响电感电流和电容电压的纹波,而且纹波幅值随着分数阶阶数的降低而逐渐增大。 (2)电感和电容的分数阶阶数会影响SEPIC的动态特性,且随着阶数的降低,表现出更好的动态性能:响应速度更快、超调量更小、到达稳定的时间更短。 (3)SEPIC的整数阶模型是分数阶模型的一个特例。在实际应用中,通过测量实际电感和电容的分数阶阶数,利用分数阶模型进行分析,可以使分析结果更准确;同时,也可以利用分数阶模型,构造特定阶数的分数阶电感和分数阶电容,设计动态性能更好的分数阶变换器。 在MATLAB/Simulink平台进行了仿真试验,仿真结果和理论分析一致,验证了SEPIC分数阶模型的正确性。3 SEPIC变换器分数阶建模与特性分析
3.1 分数阶状态平均模型建模
3.2 静态工作点与电流、电压纹波


3.3 小信号模型
4 仿真验证
4.1 分数阶数学模型

4.2 分数阶电路模型

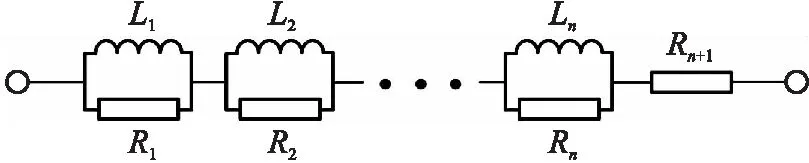
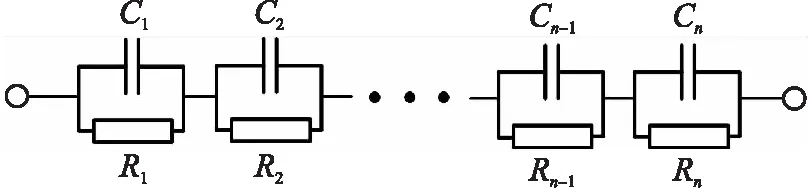
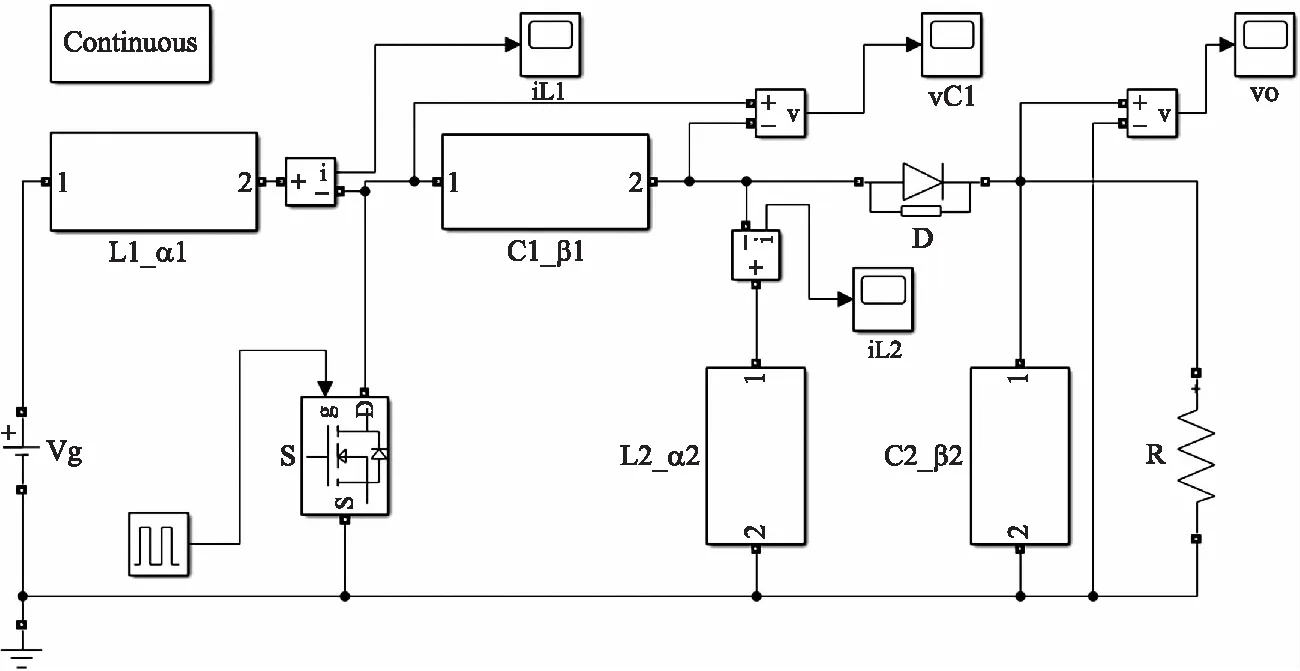



5 结论
