融合景点季节演变信息的旅游推荐算法

黄士新,左华煜,李 慧,於跃成

(江苏科技大学 计算机学院,江苏 镇江 212100)

大量用户在访问包括大众点评、Foursquare或Yelp等社交网络(Location-based social networks,LBSN)平台时,除了浏览信息外,还会对自己体验过的旅游兴趣点进行评论和打分[1]。这些在LBSN平台中积累的大量与旅游相关的信息为改善旅游用户数据稀疏,设计新的旅游景点推荐算法提供了有效保障[2]。

当前,基于协同过滤的推荐算法仍是旅游兴趣点推荐的主流方法之一[3,4]。然而,现有的这些方法往往只是采用了用户的历史签到数据,并需要通过相似性扩展来改善数据稀疏与冷启动现象[5]。近年来出现的社交推荐算法表明,利用社交网络中的用户数据可以显著改善上述问题[6]。为此,对于旅游景点推荐来说[7],一方面可以利用用户签到等多媒体数据来学习用户偏好[8],另一方面还可设计考虑景点位置[2,9]、景点类别、景点知名度[10]、旅行代价及用户对旅游景点的情感因素[11,12]等旅游景点本身固有特性的旅游推荐算法。LSBN平台上的信息往往隐含了用户与旅游景点之间存在的各种关联[13]。近年来,基于协同过滤的旅游景点推荐算法更多的是利用了LSBN平台中隐含的地理位置信息[14,15],并综合运用社交媒体和近邻朋友等社交关系[16-18],以提升旅游推荐算法的性能。

上述方法在学习用户行为与景点之间的关联时,通常将景点的所有特性视作一个整体,并未考虑不同特性在影响不同用户的行为时存在的差异性。事实上,设计旅游推荐算法时应该考虑旅游景点的地理位置、景点知名度和景点类别等不同的方面对用户决策时的不同影响程度[19,20]。此外,LSBN平台的用户签到数据中还隐含了用户行为与旅游景点在时间上的关联,而时间因素也是设计旅游景点推荐算法时需要考虑的重要因素之一[21]。事实上,对于同一个旅游景点来说,旅游景点在不同季节的游玩项目和景观特征对不同群体的用户有着不同的吸引。

直觉上,大众群体和用户个体对旅游景点的评分存在偏置,地理位置、景点类别、知名度等景点本身固有的特性也会对用户评分产生偏置。旅游景点的游玩特性和观赏效果与季节变换之间存在的固有关联也必然会对景点的人流量和到访用户的评分产生影响。换句话说,同一个旅游景点在不同季节呈现出的景观存在差异性,景点在不同时期的景观特色对不同群体的用户的吸引力也不尽相同。基于上述考虑,本文在设计旅游推荐算法时,将旅游景点的地理位置和类别等不会随着季节演变而发生变化的属性视为景点静态方面的特性,而将到访游客数量以及与之有着密切关联的景点知名度等随着季节演变而发生变化的属性视为景点动态方面的特性。为此,本文提出了一种融合景点季节演变信息的旅游推荐算法(Tour recommendation algorithm integrating seasonal evolution information of scenic spots,TRAISEI)。这方法以奇异值矩阵分解方法为基础,设计定量刻画旅游景点中静态方面和动态方面属性的偏置函数,并将其作为新的偏置项融入Bias SVD模型,以提高用户评分的预测精度,提升个性化旅游推荐算法的性能。

1 相关方法

在现实生活中,不同用户有着自身的评分习惯,不同的项目也有着自身独有的特性。类似地,特定项目获得的评分也会受到项目自身固有属性的影响,从而造成不同项目在评分时的偏差。基于上述观察,如式(1)所示,BiasSVD模型在评分预测函数中引入了用户偏置项和项目偏置项[22]

(1)

(2)

式中:目标函数的第1项为真实评分和预测评分之间的误差平方和,第2项为正则化项,λ为正则化系数。

2 融合景点季节演变信息的旅游推 荐算法

传统的BiasSVD模型将用户评分习惯和项目自身属性视为影响用户评分预测的因素,在用户评分预测函数中增加了用户偏置项和项目偏置项[22]。而Sentiment Utility Logistic Model(SULM)模型则在扩展BiasSVD模型的基础上进一步细化了兴趣点的不同方面对用户情感的影响[19]。受此启发,考虑到旅游景点的固有属性和用户选择旅游景点时的实际情况,本文将静态方面的特性在项目推荐时产生的偏置称之为静态偏置。静态偏置类似于传统BiasSVD模型中的项目偏置,本文仍然以符号bj表示。相应地,本文定义与时间相关的动态偏置,以准确刻画景点的动态方面的特性对用户决策的影响程度。

2.1 景点动态偏置

对于旅游景点而言,有些旅游景点的观赏效果和旅游体验与一年之中的季节变换关系紧密,这必然会导致同一旅游景点在不同时段的人流量和用户评分出现一定程度的差异。换句话说,在旅游景点的众多属性中,人流量以及与之紧密关联的景点知名度所产生的动态偏置会随着时间的演变而产生动态的变化。设p(j,t)为景点j在t时段的景点热度,则景点热度p(j,t)可以按照式(3)来计算

(3)

式中:Njt表示在t时段内景点j中的签到用户数量,t∈[1,12]对应于一年中的12个月,C表示景点j所在城市里全部景点的集合。由此可见,景点热度p(j,t)实际描述了t时段内景点j的签到人数在其所在城市的所有景点的签到人数中的占比。

如前所述,相比于传统BiasSVD模型中的项目偏置,景点项目的偏置包含了静态偏置和动态偏置两个部分。静态偏置bj的处理方法与BiasSVD相同,动态偏置函数bjt的定义如式(4)所示

(4)

这样,景点j在t时段的中的项目偏置bj(t)可以式(5)表示

(5)

2.2 TRAISEI模型

类似于式(1),TRAISEI的评分预测函数中同样包含了全局层面的用户平均评分、用户个体的偏置和项目个体的偏置。然而不同于传统的BiasSVD,在定义项目偏置时,TRAISEI模型考虑了景点季节变换对景点的到访人群数量、景点热度和用户评分所产生的影响。为此,TRAISEI模型的预测评分函数可以式(6)表示

(6)

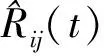
TRAISEI模型的目标函数中仍然采用误差平方和作为度量准则,以最小化预测评分和真实评分之间的误差,并通过正则化项来防止过拟合。但是不同于BiasSVD及SULM,TRAISEI模型中将景点属性中与时间关联的属性视为动态方面,预测评分时按照景点季节的不同时段来分别处理。结合式(5)和(6),TRAISEI模型的目标函数可以式(7)表示

(7)

式中:Rij(t)为t时段用户i对景点j的真实评分,目标函数的第1项度量了t时段用户对景点的真实评分和预测评分之间的误差平方和,第2项为正则化项,λ为正则化系数。

2.3 TRAISEI算法设计

Ui←Ui+α(Eij(t)Vj-λUi)

(8)

Vj←Vj+α(Eij(t)Ui-λVj)

(9)

bi←bi+α(Eij(t)-λbi)

(10)

bj←bj+α(Eij(t)-λbj)

(11)

(12)

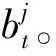
表1 TRAISEI旅游推荐算法

3 实验

为了验证本文算法的有效性,评估算法在旅游推荐时的性能,本文选用FunkSVD、PMF、BiasSVD和SVD++等模型作为对比模型,并在真实数据集上进行了模型参数选择和算法性能对比的实验。

本文实验采用3.60GHz Inter(R)Core(TM)i7-9700K处理器,16 GB内存和64位Windows 10操作系统。实验环境按照Python3.6版本配置,并使用PyCharm集成开发环境,涉及到的第三方类库主要包括metric、beautifulSoup、numpy和matplotlib。

3.1 实验数据集

本文采用的实验数据集为公开数据集yelp,数据集上包含有商家数据集、用户信息数据集及用户签到数据集等,其中商家数据集的大小为145 MB,包含有20多万个商家的信息。本文在实验时主要采用了Yelp数据集中的商家信息及用户的签信息。公开数据集Yelp中的商家数据集和签到数据集中不仅包含有与旅游景点相关的数据,还包含有酒店、餐馆等其它行业的数据。

为了验证算法在旅游推荐中的性能,本文仅采用Yelp网站上提供的与景点相关的标签。根据景点的商家编号,本文从约800万条用户签到数据集中筛选景点签到数据,共获得3 315个景点的123 467条景点签到数据。表2展示了签到数在不同数量级上所对应的景点数量。

表2 景点签到数量分布

3.2 实验结果及分析

为了衡量评分预测的准确度,采用均方根误差(Root mean square error,RSME)和平均绝对误差(Mean absolute error,MAE)作为模型推荐效果的评价指标。本文实验采用交叉验证方法,将3.1节中获取的景点数据集划分为5个子集,并以80%的数据作为训练集,20%的数据作为测试集。实验时采用梯度下降的方法进行优化迭代,每次设定的迭代次数均为100次,并以5次实验的均值作为RSME值和MAE值的最终结果。在以矩阵分解为基本方法的推荐模型中,隐变量维度k是一个可调参数,当参数k取不同的值时,模型的RSME值和MAE值往往也会发生变化。包括本文方法在内的5个模型在不同k值下RSME值和MAE值的对比情况分别如表3和表4所示。

表3 全数据集上的RSME值

表4 全数据集上的MAE值

表3和表4的实验结果表明,随着k值的增加,包括本文方法TRAISEI在内的5种方法的预测精度都会随之改善。然而,对于FunkSVD来说,k的值变化并不能明显改善该模型的预测效果,其根本原因在于FunkSVD模型并没有考虑用户和项目在个体特征方面存在的差异。此外,SVD++作为BiasSVD模型的扩展,既考虑了用户和项目偏置,又添加了用户评分的反馈信息。然而,从表6的实验结果来看,当k值较小时,SVD++模型的MSE值略小于BiasSVD,但随着k值的加大,SVD++模型的MAE值变得略大于BiasSVD。而从表3的实验结果来看,无论k的取值如何,SVD++模型的RSME值均大于BiasSVD。从景点签到数据集的特征来看,只有少量的用户到访过较多的景点,大多数用户到访的景点只有几个,甚至只有一个。因此,对于这种数据十分稀疏的景点数据,用户的反馈信息变得更加稀疏。这也导致了SVD++模型无法有效利用用户的反馈信息来改善预测精度,反而会因为这类信息过于稀疏而降低了模型的性能。

从表3和表4的实验结果来看,相比于其它4个模型,TRAISEI模型只是在k的值为10时,SVD++模型的预测性能与其较为接近。当k取其它值时,TRAISEI模型的MAE值和RSME值均要小于其它模型。这是因为用户在到访景点和对景点进行评分时往往与景点的观赏效果直接相关,而景点的观赏效果又与季节变化直接相关。而TRAISEI模型在处理各种偏置时,充分考虑了时间变化对用户到访数量和评分的影响,从而能够更好地学习用户偏好,更为准确地预测用户评分。

为了进一步验证本文算法在景点推荐上的有效性,将上述景点数据集中时间信息缺失的数据加以剔除,并在此包含丰富时间信息的景点签到数据集上重新运行了上述5种推荐模型。表5和表6分别记录了这5种模型在含丰富时间信息数据集上的RSME值和MAE值。

从表5和表6的实验结果来看,这个数据集由于包含了较为丰富的时间信息,游客的签到数据和评分数据更为客观地体现了游客对景点观赏效果的偏好,因此考虑了景点季节变换因素的TRAISEI模型的RSME值和MAE值均明显小于其它4种模型,取得了最佳的推荐效果。

表5 含丰富时间信息数据集上的RSME值

表6 含丰富时间信息数据集上的MAE值

4 结论

本文以带偏置的矩阵分解模型BiasSVD为基础,通过设计景点动态偏置函数来描述游客行为与景点季节变换在时间方面的关联,并将其引入目标函数。这样,TRAISEI模型既全面考虑了旅游景点的静态属性对用户行为的影响,又准确刻画了景点中随季节变换而动态演变的属性。真实数据集Yelp上的实验结果表明,本文算法在旅游景点上的推荐性能要优于FunkSVD、PMF、BiasSVD和SVD++等多种矩阵分解推荐算法。