短波通信的多进制LDPC 编码技术分析
2023-11-29海军潜艇学院李诠娜楚涓孙晓磊
海军潜艇学院 李诠娜 楚涓 孙晓磊
围绕短波通信编码问题展开分析,探究短波通信传输过程中适用的信道编码方法。基于此,本文首先简要分析了短波通信系统结构,结合短波通信系统展开多进制LDPC 编码仿真研究,经仿真对比后发现多进制LDPC 编码在稳定性、抗噪能力、传输速率以及误码率、噪声适应性方面存在显著优势,并进一步从高斯消元编码及系统形式编码两个角度探讨了短波通信系统多进制LDPC 编码技术,以供参考借鉴。
在无线通信系统中,短波通信属于重要组成部分,具备成本可控、灵活性高、结构简单的优势,故被广泛应用至现代通信领域中。为保障短波通信可靠性、稳定性及有效性,需灵活运用信道编码技术,而在整个信道编码技术中,最为常用的为LDPC 编码技术,即低密度奇偶校验码,而多进制低密度奇偶校验码因性能优异而备受业界关注,故本次围绕短波通信的多进制LDPC 编码技术展开研究是极具现实意义的。
1 短波通信系统结构分析
短波通信多借助电离层反射原理实现通信传输,其波长范围为10 ~100m,在具体通信传输期间,电波与地面、电离层反复反射,在反射过程中完成电波传输。在该短波通信结构下,需结合通信需求合理确定短波频率,在较小发射功率应用下完成信息通信,将信息传输至指定远距离节点[1]。但结合实际通信传输效果来看,短波通信受到电离层易受大气因素影响而出现传输不稳现象,具有时变特征,导致信息传输期间出现大量噪声,严重影响信息传输效果。
对数字短波通信系统结构进行总结,其结构框架如下:信源→信源编码→信道编码→数字调制→发射机→信道→接收机→数字解调→信道译码→信源译码→信宿,短波通信传输期间难以规避噪声问题,而一旦产生噪声则会大幅降低短波通信传输稳定性,导致通信发射端原始信息无法精准无误地被传输至接收端,由此形成误码,因此对于通信行业而言,短波通信噪声控制及技术稳定性始终属于热点问题,需通过提升信号传输可靠性而保障传输效率。
以往研究中对短波通信传输具有错误认知,认为信号传输可靠性与传播速率之间存在对立关系,信号传输速率与误码率之间成正比,即信号传输速率越高则误码率越高,在该错误认知下片面性认为短波通信无法实现无误码率。克劳德·香农经长期研究后提出了香农-哈特莱定理,明确了有扰信道性质,并指出可依托于信道编码消除信号传播速率与可靠性之间的对立关系。该信道编码定理中指出,若信道容量大小在离散无记忆信道中超出信号传输速率,当码长度足够时则可于符号集合中找到相对应的译码,此为香农第二定理。在此基础上,罗伯特·加拉格进一步提出低密度奇偶校验码(LDPC码)及其编码、译码方式。在短波通信实践中,低密度奇偶校验码(LDPC 码)表现出优异编码性能,成为短波通信系统常用编码技术[2]。
2 基于短波通信系统的多进制LDPC 编码仿真
2.1 LDPC 码
低密度奇偶校验码(LDPC 码)为线性分组码,将其码长、信息数据位长度分别设定为N、K,此时可用M=N-K 关系式确定低密度奇偶校验码(LDPC 码)长度,在此基础上运用R=K/N 关系式确定LDPC 码率,并生成校验矩阵H,大小为M×N。如图1 所示为LDPC码双向图结构,可运用该双向图表示低密度奇偶校验码矩阵,结合图1 来看,将低密度奇偶校验码划分为两组,将其中一组设定为N 个节点,用于代指N 个信息位,此时所设定的节点为信息节点,在该结构中,矩阵列与节点信息位相互对应。将另一组设定为M 个节点,用于代指M 个校验位,此时所设定的节点为校验节点在该结构中,矩阵行与节点校验位相互对应。在此基础上,连接各个校验节点,同时将连接而成的直线看作“边”,而“边”的数量则为校验节点,随机选取节点出发,经过多道“边”则能够再次回到出发节点,而此时的“边”则构成了完整环路[3]。在短波通道系统双向图中可清晰化了解LDPC 码具体传输情况,并可结合LDPC 码传输情况判断短波通道传递可靠性,同时可采用该方式检验得出LDPC 码误码率数据。在短波通信LDPC 码发展之初仅有二进制LDPC 码,而以二进制LDPC 码为基础逐渐延伸出多进制LDPC 码,与二进制LDPC 码相比较,多进制LDPC 码校正矩阵具有更多维度,而其同样可借助双向图进行表示。相较于二进制LPDC 码,在短波通信系统结构中,多进制LDPC 码因实现校正矩阵的拓展延伸,故在信息传递期间能够表现出更高抗噪性,可良好应对短波通道噪声问题。

图1 LDPC 码双向图结构Fig.1 LDPC code bidirectional graph structure
2.2 编码仿真
2.2.1 编码处理
在短波通信系统结构中,多进制LDPC 码能够采用不同方法进行构造,为验证不同编码构造效果而展开仿真分析,其中选取GF(4)、GF(8)两个有限域作为多进制LDPC 码,此外,于编码前,需对两个有限域进行编码设定。(1)GF(4)有限域原始码(K)被设定为3000,完成编码后其码长(N)为9000,在此情况下,所需校验方程码率(R)、数量位(M)分别为1/3、6000,最大列重、最大行重分别为3、4。(2)GF(8)有限域原始码(K)被设定为2000,完成编码后其码长(N)为6000,GF(8)有限域的校验方程码率、数量位及最大列重、最大行重均与GF(4)有限域一致。上述所构建的GF(4)、GF(8)两个有限域多进制LDPC 码校验矩阵较为稀疏,且码率相对较低,为了解多进制LDPC 码优势,同样对二进制LPDC 码进行仿真,于二进制LPDC 码编码之前,将其GF(2)原始码(K)设定为6000,完成编码处理后,其码长(N)则会转变为18000,在此情况下二进制LPDC 码的校验方程码率(R)、数量位(M)分别为1/3、12000,最大列重、最大行重分别为3、4。
2.2.2 仿真分析
将GF(4)、GF(8)及GF(2)三种编码仿真情况进行对比,其对比结果如图2 所示。结合图2 分析GF(2)、GF(4)、GF(4)之间的递进关系,不难看出,随着有限域的增加,LDPC 码符号可取值数量不断增加,编码性能逐渐提高,以10-5误码率标准来看,二进制LPDC 码信噪比高于四进制码,差值为0.2dB,而四进制LPDC 码信噪比又高于八进制LPDC 码,约高出0.1dB。步入衰减区阶段后,GF(4)、GF(8)及GF(2)三种编码均快速衰减,而其中二进制LPDC 码衰减最慢,从这一角度来看,LDPC码元素数量与衰减速度之间成正比,即元素越多则衰减越快,该特征同样可作为多进制LDPC 码优势性能。
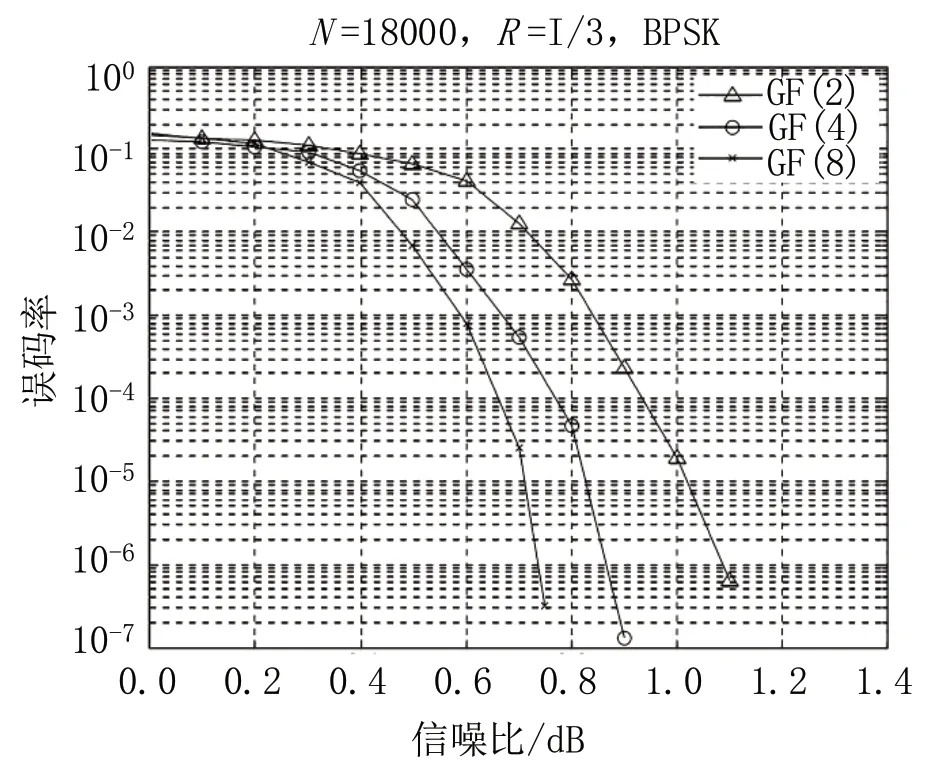
图2 GF(2)、GF(4)、GF(8)三种编码仿真结果Fig.2 Simulation results of GF (2), GF (4), and GF (8) encoding
2.2.3 误码率对比
为进一步了解多进制LDPC 码算法误码率,以GF(4)编码为实例展开仿真对比分析,将GF(4)编码进行设定,其码长由编码前的3000 转变为编码后的9000,对于该编码,其校验方程码率(R)、数量位(M)分别为1/3、6000,最大列重、最大行重分别为3、4。在多进制LDPC 码算法误码率仿真对比期间,所运用的译码算法分别为LLR-FFT-SPA、FFT-SPA,旨在通过对比两种译码算法而了解短波通信系统结构中多进制LDPC 码算法误码率。如图3 所示,LLR-FFT-SPA、FFT-SPA 两种译码算法在误码率方面较为相近,结合10-5误码率标准来看,两种译码算法信噪比性能仅相差0.01dB[4]。而经综合对比后可知,与FFT-SPA 译码算法相比,LLR-FFT-SPA 的硬件资源需求量较低、复杂程度较低,故所表现出的算法运算可靠性较高。若借助该算法进行多进制LDPC 码译码,则可有效精简算法结构,可在一定程度上降低短波通道系统结构复杂程度。经上述方针对比分析发现,多进制LDPC 编码技术在信噪比性能方面优于二进制,依托于短波通信方式传输信号时,可借助多进制LDPC 编码技术对信息传输期间的噪声加以控制,尽可能降低噪声对于短波通信信息传输的负面干扰。
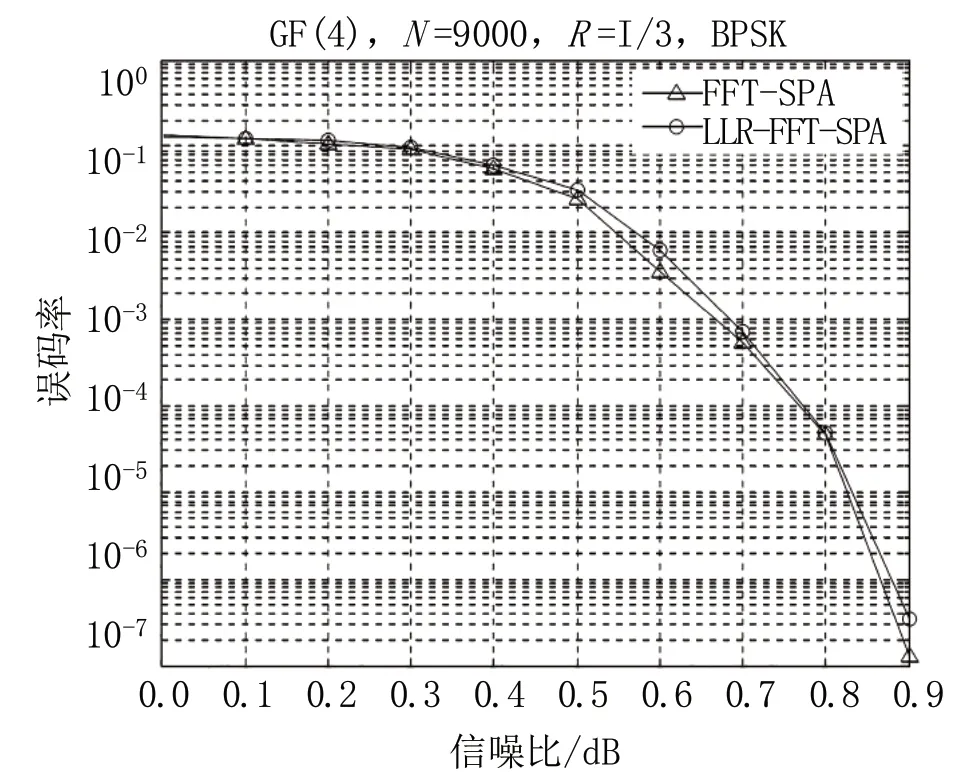
图3 FFT-SPA、LLR-FFT-SPA 译码仿真结果Fig.3 FFT-SPA and LLR-FFT-SPA decoding simulation results
3 基于短波通信系统的多进制LDPC 编码技术探讨
3.1 高斯消元编码
经上述仿真对比分析后发现,在短波通信系统内,多进制LDPC 编码技术的抗噪性能更为优异,能够有效控制信噪比,减少噪声对于信号传输过程的干扰。但结合短波通信系统结构分析可知,无论是二进制还是多进制LDPC 码,均面临编码复杂这一问题,若LDPC 码长度较大,则会接近香农极限,继而影响了LDPC 码在短波通信系统中的应用,与此同时,LDPC 码校验矩阵同样较大,给短波通信校验矩阵存储及编码、译码造成一定难度。针对该问题,需结合短波通信系统结构选择适宜的多进制,LDPC 编码技术,依托于简单编码算法而保障短波通信系统编码速度及信号传输稳定性。
应用高斯消元法时应注意,编码运算过程中涉及GF(q),运算期间所确定的校验矩阵虽较为稀疏,但经编码运算后,其所产生的生成矩阵通常较为复杂而不再稀疏。编码后的生成矩阵具有较大存储量,在此情况下,若将生成矩阵与信息序列相乘运算,所产生运算量较为庞大,且码长多为幂级数。因此,从短波通信系统结构角度来看,高斯消元编码技术虽较为简单,但该编码方式所产生的时间复杂度、空间复杂度均较高,故在短波通信系统结构中应谨慎应用。
3.2 系统形式编码
若将短波通信系统结构中的LDPC 码看作系统码,则在LDPC 编码期间,可将(N,K)编码序列中前K 个码字视为输入值,而后续(N-K)个码字则属于校验码字,在该情况下进行短波通信系统结构编码时,仅需对(N-K)校验码字进行运算即可。将系统形式编码技术应用到短波通信结构系统中时,可将校验矩阵划分两个矩阵,记为H1与H2,而H1与H2可分别记为K×K、K×(N-K),在该矩阵中,矩阵H1与H2分别为信息码字与校验码字。在此基础上对编码后序列进行拆分,确定单个信息码字长度及校验码字长度,在整个编码结构中,短波通信中的H1矩阵、H2矩阵均为H 矩阵的子矩阵,而H 矩阵属于稀疏矩阵,因此,所设定的信息码字矩阵H1与校验码字矩阵H2均呈现出稀疏特征。但在短波通信系统结构中,校验码字矩阵H2-1通常并不表现出稀疏特征,但受到信息码字矩阵H1的稀疏性影响,将矩阵H2-1与H1相乘时,无需全部计算得出矩阵内全部元素,此时按照短波通信系统信息传输需求完成特定元素的乘积运算即可。此外,在该情况下,多进制LDPC 编码H2矩阵的逆矩阵同样可基于短波通信系统信息传输需求,将相关矩阵算法结果实时存储至本地系统内,借助该方式消耗短波通信系统传输存储空间,起到控制多进制LDPC 编码算法运算量的作用。
总而言之,系统形式编码技术的应用有助于结合短波通信需求选择适宜的编码矩阵,在确定多进制LDPC编码数据量及码长基础上对矩阵复杂性进行控制,尽可能构建稀疏矩阵进行算法运算,在允许范围内降低矩阵算法运算量,把控短波通信系统结构码长线性程度。结合上述两种短波通信多进制LDPC 编码技术分析发现,选取多进制LDPC 编码技术时,需注意把控编码矩阵复杂程度,对时间复杂度、空间复杂度进行控制,不可仅关注编码方式本身的难易程度,应从多角度统筹分析,继而选取出最为符合短波通信系统结构的多进制LDPC编码技术。
4 结语
综上所述,与二进制相较,多进制LDPC 编码技术在短波通信系统结构中的应用性能更为优异,而为了了解多进制LDPC 编码技术性能,在明确短波通信系统结构基础上,采用仿真对比的方式进行二进制、多进制LDPC 编码分析,经对比确认了多进制LDPC 编码技术在信噪比性能方面的优势,并详细分析了短波通信系统结构的多进制LDPC 编码技术,即高斯消元编码及系统形式编码。
