关于加权Coxeter 群的胞腔理论的综述
2023-11-29时俭益
时俭益,黄 谦
(1.华东师范大学 数学科学学院,上海 200241;2.山西大学 数学科学学院,太原 030006)
0 引 言
记Z为整数集,N 为非负整数集,N+为正整数集,对于Z中任意的i≤j,记[i,j]为集合{i,i+1,···,j},简记集合[1,j]为[j].设W是Coxeter 群,S是其 Coxeter 生成元集合.设ℓ是长度函数,≤ 是群W上Bruhat-Chevalley 序.为了构造W及其Iwahori-Hecke 代数H(W)的表示,文献[1]介绍了某些等价类,称之为群W的左胞腔、右胞腔和双边胞腔,每个胞腔可以给出W和H(W)的某个表示.之后,文献[2]在(W,S)上定义了权函数L,并称(W,S,L)为加权Coxeter 群.文献[2]还定义了相应的Iwahori-Hecke 代数H(W,S,L),并把(W,S)上的左胞腔、右胞腔和双边胞腔的概念推广到(W,S,L)上,这也可以给出(W,S,L)和H(W,S,L)的某个表示.
文献[2]通过H(W,S,L)的结构系数定义了函数a和W上独异对合元集合D.随后就(W,S,L)的胞腔、a函数和D中元素等方面提出了15 个猜想.这些猜想将分裂情形下有限或仿射Coxeter 群胞腔方面的已知结果拓展到一般的加权Coxeter 群.
对于任意给定的加权Coxeter 群(W,S,L)(其中L可取W上任意权函数),清晰地刻画其胞腔是一个大工程,尤其对于那些权函数在S上不取常值的情形(此时称(W,S,L)为不等参数情形).当W是型Im(m是偶数或∞),F4,和时,分解工作已经完成[2-5],而W是型Bn,和,n >2,的分解工作已经部分完成[6-15].
本文给出了本研究团队在胞腔分解方面工作成果的一个综述.
第1 章是预备知识,罗列了加权Coxeter 群胞腔方面的一些概念和已知结果以备后用.第2—4 章详细描述了在拟分裂情形下仿射Weyl群的胞腔理论方面本研究团队所取得的成果.第5 章简要描述了拟分裂情形下仿射Weyl群中满足条件a(Γ)≤6 的胞腔Γ和一般情形下加权泛 C oxeter 群的胞腔分解.
1 预备知识
本章罗列了文献[2]中加权Coxeter 群胞腔方面的一些概念和已知结果以备后用.
设L:W →Z 是Coxeter 群(W,S)上函数,如果对于任意满足条件ℓ(wu)ℓ(w)+ℓ(u)的w,,有等式L(wu)L(w)+L(u),则称L为(W,S)上权函数,(W,S,L)为加权Coxeter 群.明显地,长度函数ℓ本身是权函数,称(W,S,ℓ)为分裂情形.
设Wα|α(w)w},这里α是W的满足条件α(S)S的群自同构.对于S中任意α-轨道J,如果W的由J生成的子群WJ是有限子群,则记wJ为WJ的最长元,它落在Wα里.设Sα是由元素wJ组成的集合,其中J取遍S的α-轨道.那么(Wα,Sα)是一个Coxeter 群,长度函数ℓ在Wα上的限制是Wα的权函数,加权Coxeter 群(Wα,Sα,ℓ)被称作拟分裂情形.
设AZ[v,v-1]是以v为变量的整系数Laurent 多项式环,根据定义,(Wα,Sα,ℓ)上的Iwahori-Hecke 代数H:H(Wα,Sα,ℓ)是A上结合代数,它有一组自由A-基{Tw|,满足:
对于任意x,,有等式cxcyz∈W hx,y,zcz,其中hx,y,z A.Lusztig[16]还定义了函数a:W →N,对任意z,满足: 对于任意x,,有关系va(z)hx,y,zZ[v]且对于某组x,,有关系va(z)-1hx,y,z/Z[v].
对于任意z,定义Δ(z)N 满足pe,znzv-Δ(z)+v的幂次严格低的项,这里nzZ{0},e是W的单位元.设D|a(z)Δ(z)}.那么当W是有限或者仿射Coxeter 群,并且(W,S,L)是在分裂或者拟分裂情形时,D是W中包含有限个对合元(对合元的意思是指阶数不超过 2 的元素)的集合.在这种情形,W的任意左胞腔L都恰包含D∩L中唯一一个元素(记为d),任意x都满足Laurent 多项式的次数关系hx-1,x,da(d)[2,17].
假定w,设R(w)|ws <w},记M(w)为包含满足如下条件的元素x的集合,即存在着W中一列元素x0w,x1,···,xrx,r≥0,并且对于每个i[r],都有xi-1,R(xi)与R(xi-1)互不包含.明显地,如此的一列元素x0w,x1,···,xrx整个都落在M(w)中,称它为M(w)中始于w的一条路.称w,有相同的广义τ-不变量,如果对于M(w)中任意始于w的一条路w1w,w2,···,wr,都存在M(y)中始于y的一条路y1y,y2,···,yr使得等式R(wi)R(yi)对于任意[r]都满足,而且交换w和y的位置该条件依然成立[9,18].
文献[2]就任意加权Coxeter 群(W,S,L)的胞腔、a函数和D中元素提出了15 个猜想.当这些猜想成立时,(W,S,L)的胞腔会具有一些好的结构性质.由文献[2]可知,如果(W,S)是有限或者仿射的Coxeter 群,并且(W,S,L)在分裂情形时,这些猜想是成立的.Lusztig[2]提出这些猜想就是为了能够将(W,S)上胞腔的一些结果由分裂情形推广到一般情形中.当(W,S,L)在拟分裂情形时,Lusztig[2]证明了这些猜想成立.
2 拟分裂情形下加权仿射Weyl 群(,S,)
对于tZ和i[0,m],任意的w可由(m+1)-元组((1)w,(2)w,···,(m+1)w)确定,如果对于j[m+1]有等式(j)wij,则可记w[[i1,i2,···,im+1]].
这里当m2n-1,2n}时,ϵm,n1 ;当m2n+1 时,ϵm,n0 .如果m2n-1,对于[n-1],令tisis2n-i,t0s0,tnsn;如果m2n,对于i[n-1],令tisis2n+1-i,t0s0,tnsnsn+1sn;如果m2n+1,对于i[n-1],令tisis2n+1-i,t0s0s1s0,tnsnsn+1sn(图1),这样就给出了的Coxeter 生成元集合.
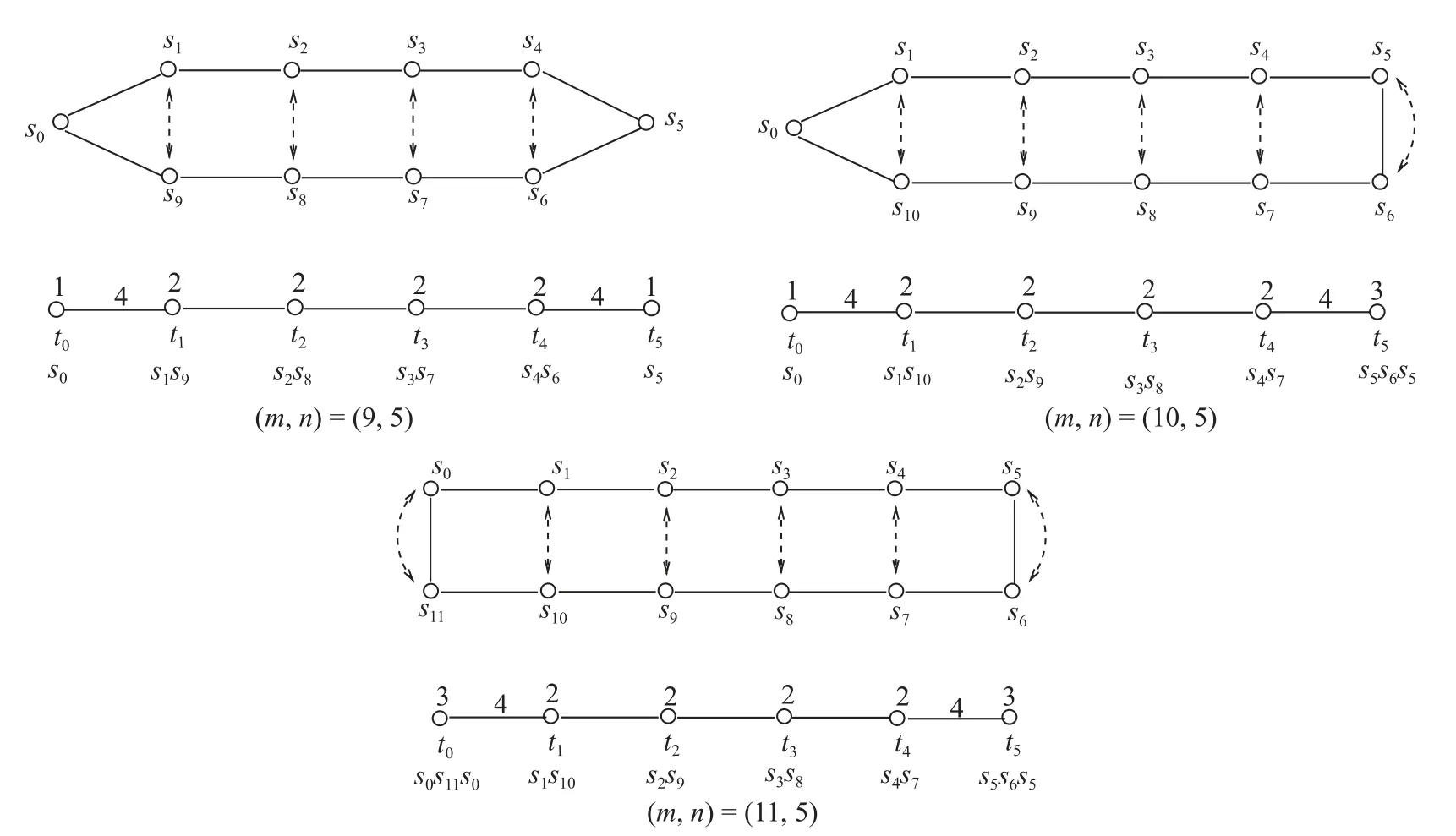
图1 αm,n在Γ()上的作用,(m,n)∈{(9,5),(10,5),(11,5)}Fig.1 The action of αm,n on Γ()with(m,n)∈{(9,5),(10,5),(11,5)}
固定w,对于[m+1]中任意i/j,如果存在某个p,Z 使得p(m+1)+i >q(m+1)+j和(p(m+1)+i)w <(q(m+1)+j)w成立,则记作i≺w j,这样就定义了集合[m+1]里的一个偏序.如果i ≺w j或者j≺w i,则称i/j为w可比较的,否则,称它为w-不可比较的.
如果集合[m+1]中的数列满足a1≺w a2≺w···≺w ar,称a1,a2,···,ar为w链.有时会将w链a1,a2,···,ar等同于相应的集合{a1,a2,···,ar}.对于任意k≥1,定义k-w-链族为[m+1]中k条w链X1,X2,···,Xk的无交并.对于任意k≥1,设dk是k-w-链族最大可能的基数.设λ1d1,λk+1dk+1-dk,对于k[r-1],那么根据文献[19]中一个结果可知λ1≥λ2≥···≥λr.因此通过wψ(w):(λ1,λ2,···,λr),定义了映射ψ:→Λm+1.
如果[m+1]的子集E中元素两两w-不可比较,则称集合E是w-反链.
例 1设w[[8,-6,5,-2,11,4,15,1]],那么图2 是文献[5]中定义的偏序关系的Hasse表.在文献[5]中,a当且仅当对于某个rN,存在一个数列x0a,x1,···,xrb使得对每个i[r],都有xi-1→xi.由图可知存在w-链{2,6,3,1},2-w-链族{2,6,5}∪{4,3,1}和3-w-链族{2,6,5}∪{8,3,1}∪{4,7},每一个都是相应情形的最大可能基数.
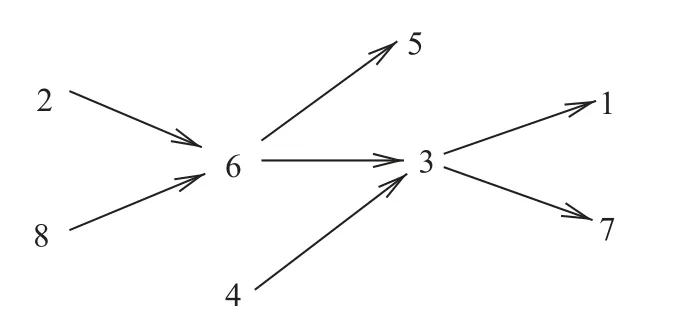
图2 偏序关系 w 的Hasse 表Fig.2 The Hasse diagram of the poset w
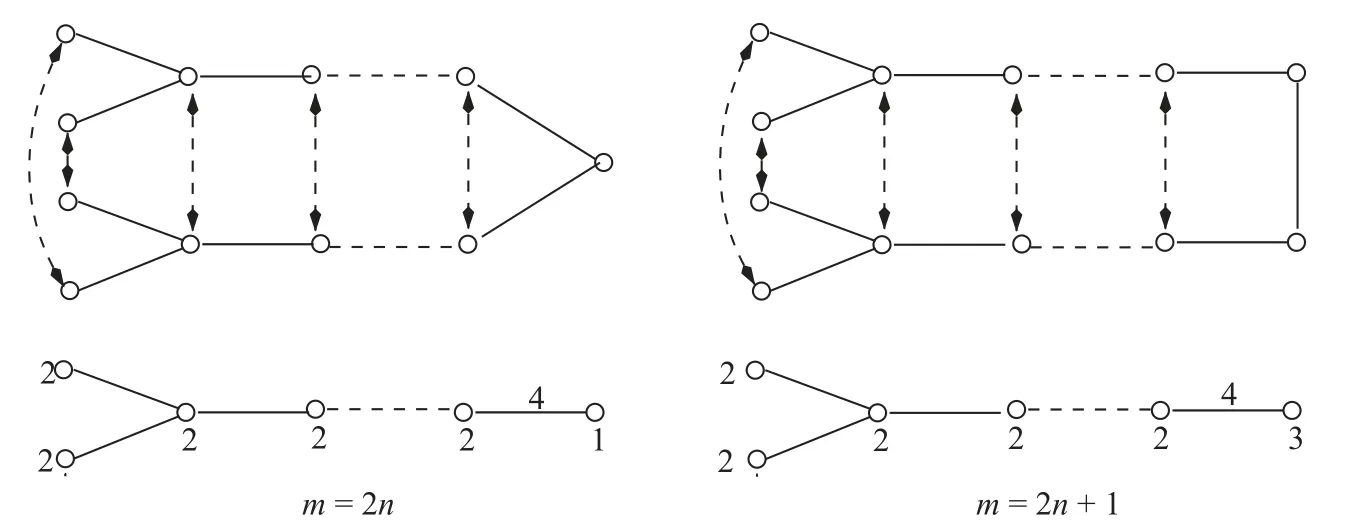
图3 αm,n在Γ()上的作用,其中m ∈{2n,2n+1}Fig.3 The action of αm,n on Γ()withm ∈{2n,2n+1}
对于任意iZ,定义 〈i〉[m+1]使满足条件 〈i〉≡i(模m+1).设 Ξ 是所有满足如下条件的元素的集合,即存在某个T(T1,T2,···,Tr)+1满足:
(i)在[r]中,如果i<j,那么对任意a,b,都有 〈(a)w-1〉≺w〈(b)w-1〉 ;
(ii)对于任意i[r],〈(Ti)w-1〉 是[m+1]中最长w-反链.
明显地,表T完全由wΞ 确定,记T为T(w).根据文献[18]可知,映射T:Ξ→Cm+1是满射.由Greene 在文献[19]中的一个结果可知,κ(T(w))ψ(w)∨.
例 2设w[[7,10,-8,1,11,5,14,-4]],那么wΞ,且T(w)({4,8},{1,5},{2,3,6,7})和ψ(w)(4,2,2)∨(3,3,1,1).
特别地,当 |Tj||Tj+1| 时,TT′.
对任意T,T′+1,如果Cm+1中存在T0T,T1,···,TrT′满足: 对于每个i[r],都存在某个整数hi,使得Ti可由Ti-1通过一个{hi,hi+1}-变换得到,则记为T≈T′.这就在集合Cm+1上定义了一个等价关系.
对于a(a1,a2,···,ar),记aop(ar,···,a2,a1),如果aopa,称a是对称的.
引理 3[15]设T,T′+1.
(3)如果T≈T′,那么T是(m,n)-自对偶的当且仅当T′也是.
由引理3(3)可知,如果等价类里某个(因此所有的)表是(m,n)-自对偶的,就称Cm+1中的≈-等价类是(m,n)-自对偶的.
3 借助于表来计算 中集合 Eλ 的左胞腔个数
对于r2 的情形,可给出一个精确公式.
命题 1[15]对于a(n+t,n-t),t[n-1],有
命题 2[15]对于a(n+1+t,n-t),t[0,n-1],有
命题 3[15]对于a(n+1+t,n+1-t),t[n],有
推论 1[15]符号如上所示,γm+1-2n(a)等于
注 1设a(r,s),其中r,N+且r+[m+1].由命题1—3 能得到γm+1-2n(a)的计算公式.注意到有r≤s的情形.如果rs,那么a是对称的,因此γm+1-2n(a)由定理2 可知;如果r<s,那么γm+1-2n(a)γm+1-2n(aop).
假设r+s <m+1,当m+1-20,2},有r+s2p和r-s2q,其中p,Z .如果r>s,那么分别替换n,t为p,q,根据式(6)可得到γ0((r,s))的个数,分别替换n,t为p-1,q,可得到γ2((r,s))的个数.当m+1-2n1,有r+s2p+1和r-s2q+1,其中p,Z .如果r>s,那么分别替换n,t为p,q,根据式(7),可得到γ0((r,s))的个数.
问题 1[15]对于满足条件a1>a2>···>ar和r≥3 的任意a(a1,a2,···,ar)m+1,能否找到关于γm+1-2n(a)的精确公式?
4 集合 Eλ 中的胞腔,其中λ Λm+1
文献[11-14]刻画了对应于某些划分λ+1的集合Eλ中的胞腔.
对于所有被研究的λ2n,已经证明了集合Eλ中的左(相应的,双边)胞腔都是左(相应的,双边)连通的(见定理4—12).时俭益猜想: 对于任意加权Coxeter 群的所有左胞腔和双边胞腔,连通性猜想也是正确的.
设η是的群自同构,由对于任意i[0,n]的等式η(ti)tn-i所确定.
(4)除了k2,3 之外,集合Ek212n-k-2对于任何其他的k都是无限的.
定理 6[13]对于k[n],设λ(2n-k,k).
(3)表 1 列出了对于任意λ6,n(λ)的值.

表1 λ ∈Λ6 时,n(λ)的值Tab.1 The value of n(λ)forλ ∈Λ6

表2 λ ∈Λ8 时,n(λ)的值Tab.2 The value of n(λ)forλ ∈Λ8
(5)表 3 对于所有λ7列出了n(λ)的值.
借助于右广义τ-不变量,通过逐个讨论,文献[25]证明了定理12.

表3 λ ∈Λ7 时,n(λ)的值Tab.3 The value of n(λ)forλ ∈Λ7
5 加权Coxeter 群的一些其他成果
定理 13[9]的满足条件a(Γ)≤6 的每个左胞腔Γ都左连通.

表4 n ≥3 ,k ∈[6]时,m2,1(n,k)的值Tab.4 The value of m2,1(n,k)for n ≥3 andk ∈[6]

表5 n ≥3 ,k ∈[6]时,m2,3(n,k)的值Tab.5 The value of m2,3(n,k)for n ≥3 andk ∈[6]
Lusztig 在文献[2]里曾猜想: 对于任意加权Coxeter 群(W,S,L),函数a:W-→N 有一个上界NmaxIL(wI),这里I取遍S中所有满足条件 |WI|<∞的子集.当(W,S,L)是有限或者仿射的加权Coxeter 群时,Lusztig[2]证明猜想成立.时俭益和杨高在文献[29]里首先对于任意加权泛Coxeter 群(W,S,L)(即等式o(st)∞对于S中任意s/t都成立)证实了该猜想,进而在文献[30]里对于Coxeter 图是完全图的任意加权Coxeter 群(W,S,L)(即对于S中任意s/t都满足关系o(st)>2)证实了该猜想.此后,时俭益和李艳在文献[31]里对于Coxeter 图的边标记都不等于3 的任意加权Coxeter 群(W,S,L)(即对于S中任意s/t都满足条件o(st)/3)证实了该猜想.
为了将加权Coxeter 群(W,S,L)在分裂情形下的一些结论推广到一般情形,Lusztig[2]提出了15 个猜想.当W是有限或者仿射Coxeter 群,(W,S,L)在分裂情形或者拟分裂情形时Lusztig[2]证实了这些猜想.M.Geck 在文献[3]对于F4型的任意加权Coxeter 群;时俭益和杨高在文献[29]对于任意加权泛Coxeter 群;J.Guilhot 和J.Parkinson 在文献[4-5]对于和型的任意加权Coxeter 群;高剑伟和谢迅在文献[32]对于秩为3 的任意加权Coxeter 群;谢迅在文献[33]对于Coxeter 图是完全图的任意加权Coxeter 群,都分别证实了这些猜想.
定理 14[29]设加权泛Coxeter(W,S,L)群满足上面的条件.
(1)a(e)0 .对于w,a(w)max{L(s)|,s≤w}.如果w,k[l],那么a(w)Lk.
(2)W的左胞腔或者是{e}或者有形状,其中k[l],s和u.(W,S,L)有无限多个左胞腔当且仅当或者l>2,或者l2且|S1|>1 .
(3)W的双边胞腔或者是{e}或者有形状,其中k[l].因此(W,S,L)的双边胞腔个数等于l+1 .
(4)W的任意左(相应的,双边)胞腔都是左(相应的,双边)连通的.
时俭益和杨高在文献[34]里将文献[29]中加权泛Coxeter 群上的结果拓展到更一般的加权Coxeter 群(W,S,L): 其中S是两个非空子集I和J的无交并,这里J:|o(st)∞,对任意(称J为S的泛部分),并且W中由I所生成的子群WI是有限的,设wI是子群WI的最长元,所研究的(W,S)中权函数L包括以下情形: ①m in{L(s)|≥L(wI);②max{L(s)|min{L(t)|;③存在t使得对于任意s,都有不等关系L(t)<L(s),并且L在J上取常值LJ,这里LJ属于[L(wI)-1]的某个子区间.时俭益和杨高在文献[34]里刻画了(W,S,L)的所有这种左胞腔和双边胞腔,它们中的每一个都与WWI有非空交.在情形 ③中,WI中权值次大的元素:wIt在讨论中起到了重要作用.文中推导出了的一些有趣性质,其中某些性质与最长元wI类似,某些有独特之处.
