基于虚拟车道线的智能车辆换道轨迹规划方法*
2023-11-29郭俊超邵金菊袁俊凯韩文祥高松
郭俊超 邵金菊 袁俊凯 韩文祥 高松
(山东理工大学,淄博 255000)
主题词:虚拟车道线 自主换道 轨迹规划 结构化道路
1 前言
复杂交通环境下的智能车辆自主换道是自动驾驶领域的研究热点和难点之一。高效平稳的换道行为可在很大程度上降低交通事故发生概率并减轻驾驶员的驾驶强度,对道路交通的流通性和驾驶安全性均有重要影响。
目前,针对具有明显车道线的结构化道路的路径规划问题已经基本解决,主要轨迹规划方法包括基于数学优化的方法[1-3]、基于采样的方法[4-6]和基于曲线拟合的方法[7-9]。在车道线不清晰或无车道线的道路条件下,合理的换道轨迹规划是相对棘手的问题。
针对上述车道线不清晰或无车道线的情况,目前主要采取短时车道保持策略或根据道路宽度进行轨迹规划。刘李漫等[10]提出一种基于虚拟车道线的车道偏离预警系统,当车道线检测不准确时,可以生成虚拟车道线,提供车道偏离预警能力。Li等[11]提出了在无车道边界、路锥改变车道、停放车辆遮挡车道标记场景中,生成虚拟道路边界完成车道跟踪的方法。宗芳等[12]提出一种基于道路横断面自动划分车道线的方法,解决了自动驾驶汽车在无车道线路段行驶时轨迹规划的问题。
本文针对车道线不清晰或无车道线的情况,提出一种基于虚拟车道线的动态环境下换道轨迹生成方法:根据环境中的车辆信息生成虚拟车道线,为自动驾驶车辆自动划分车道线,确定行驶航向;在虚拟车道内选择目标车道,利用五次多项式生成换道轨迹,同时对多项式参数进行约束,保证换道过程的舒适性和安全性。最后,将所提出的路径规划算法加入自动驾驶车辆的智能规划决策模块中进行仿真和硬件在环测试。
2 换道场景定义
车辆换道过程中,既要考虑主车的运动状态,又要考虑其他交通参与者的运动状态以及当前行驶道路的边界条件。
定义换道场景如图1 所示。A、B分别为换道车辆的初始位置和目标位置,二者间的连线表示生成的换道轨迹。以换道车辆(主车)运动方向为x轴、垂直方向为y轴,以主车在换道起始时刻的后轴中心为原点建立坐标系。其他车辆为道路中的障碍车辆。交通环境是动态变化的,在主车换道过程中,周边车辆的车速、距离等信息可通过车载传感器测得。
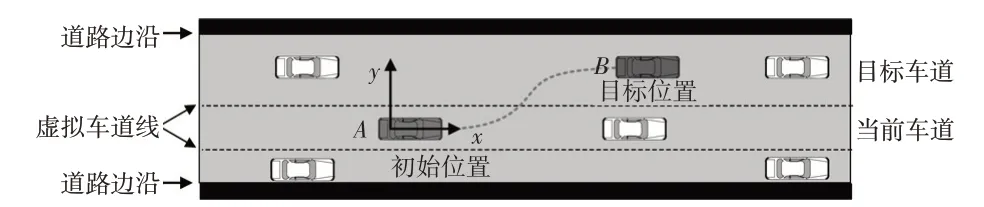
图1 换道场景示意
3 虚拟车道生成方法
虚拟车道线将车辆所处环境划分成与车辆朝向平行的多条车道,根据车道宽度、车辆的无碰撞距离、最小换道角度等约束条件选择无碰撞的最佳目标车道,用于引导车辆进行换道操作。
3.1 碰撞检测方法
在车辆创建虚拟车道线及换道的过程中,为避免碰撞,主车需要时刻与周边车辆保持一定的安全距离。通过建立车辆避障模型,结合最小碰撞距离R实现车辆避障。连接车辆后轴中心P1和前轴中心P2,建立直线车辆模型,如图2所示。分别以P1、P2为圆心,最小碰撞距离R为半径,将直线车辆模型膨胀为由圆弧和直线组成的图形。家用车宽度通常为1.8~1.9 m,为满足最窄车道宽度要求,本文设R=1.0 m。
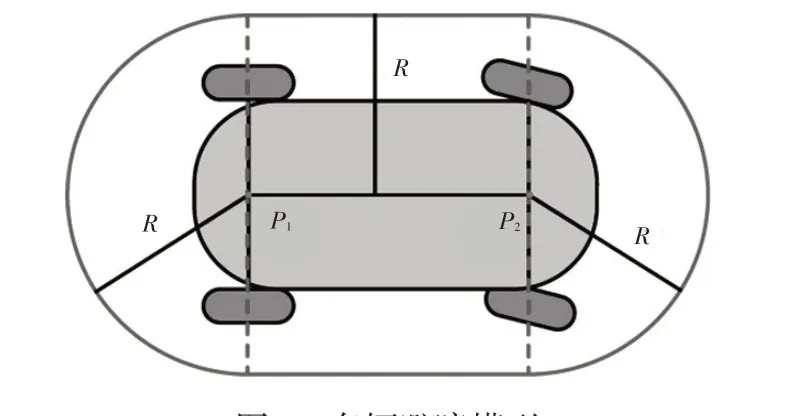
图2 车辆避障模型
3.2 虚拟车道构建方法
虚拟车道依据目标航向和主车与障碍车辆的最大距离构建。通过建立车辆避障模型,可将障碍物从世界坐标系转换到车体坐标系。设第k条车道的参数包括车道宽度w(k)、车辆的无碰撞距离d(k)和换道最小角度a(k)。其中:d(k)指主车在与障碍车辆发生碰撞前,从当前位置沿第k条车道行驶的距离,如果相邻车道具有相同的无碰撞距离d(k),则将相邻车道进行合并;a(k)指从当前车辆位置经过无碰撞区域到第k条车道的直线与x轴的夹角。虚拟车道及其参数如图3所示,图中车道总数量N=7条,将车辆开始换道时主车前方与车辆垂直的线段定义为换道起始线,车辆的可行驶空间被障碍车辆划分为不同的车道,由于车辆正常行驶时只进行前向运动,所以在车道划分时,将后方的车辆忽略。障碍车辆与主车目标航向的角度超过预先定义的角度限值rlim(k)则被定义为后方车辆。若起始线没有障碍车辆,取rlim(k)=90°,若起始线有障碍车辆,根据普通乘用车最小转弯半径及车载传感器参数特性,取rlim(k)=±60°。

图3 虚拟车道示意
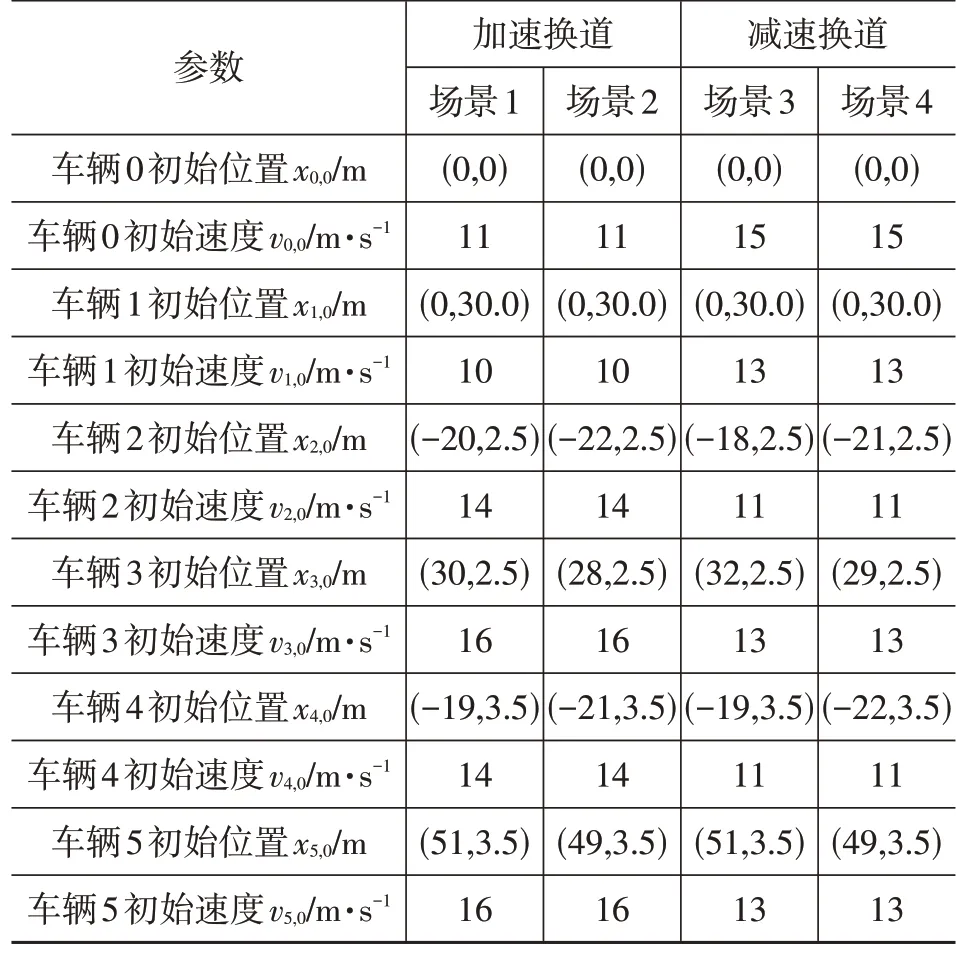
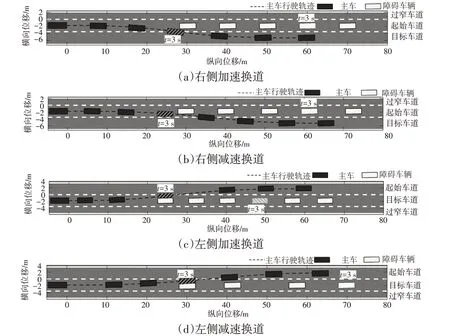
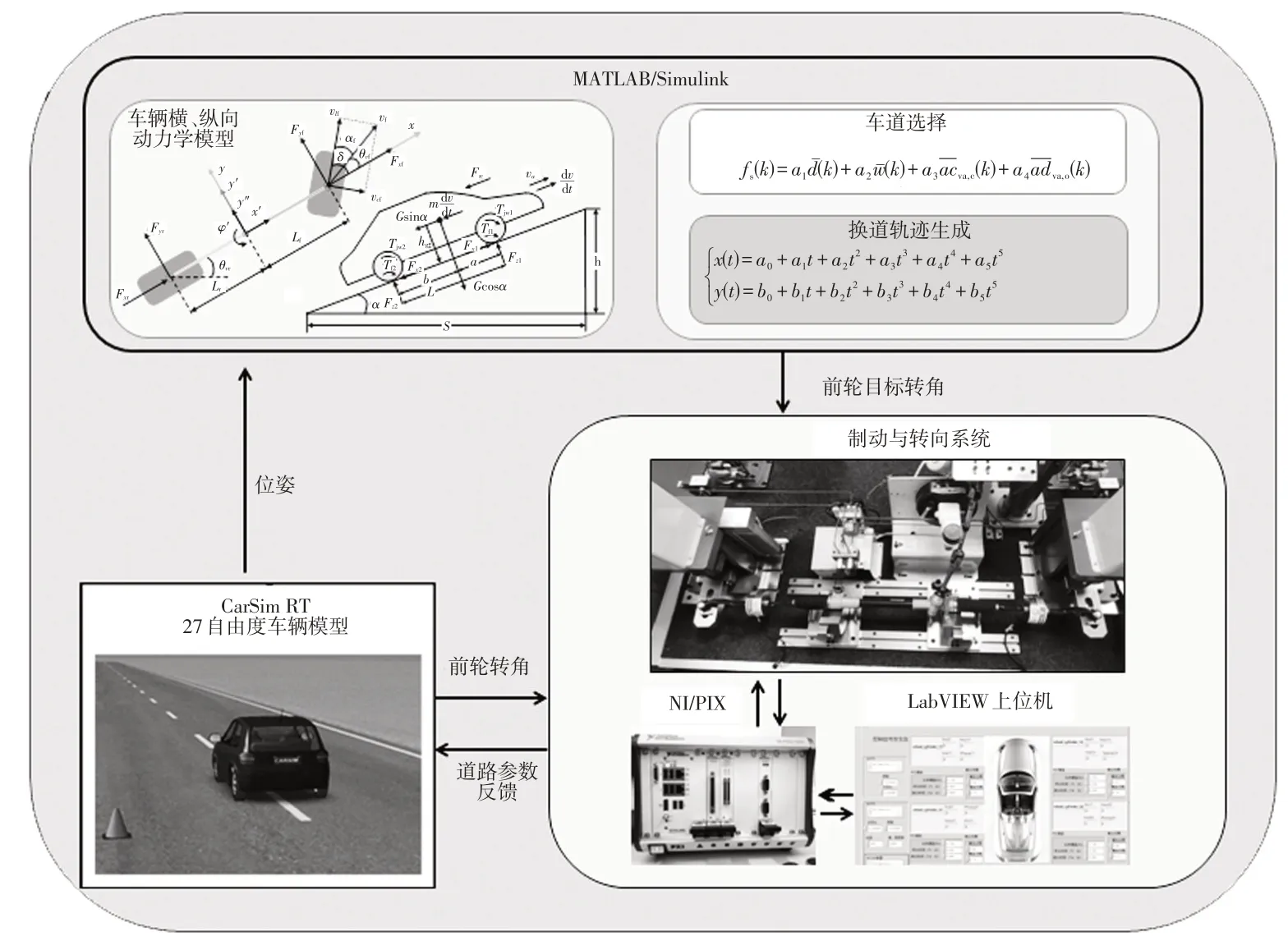
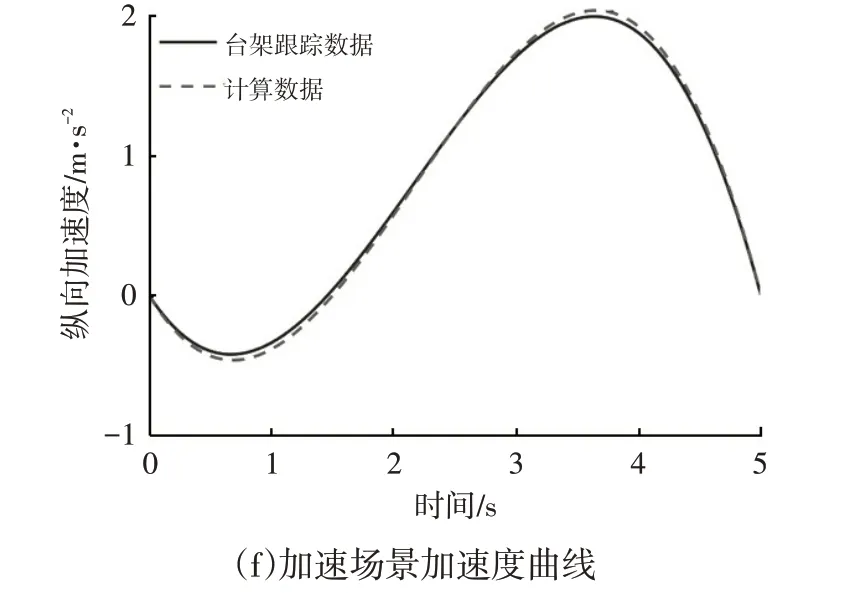
当根据障碍车辆生成的虚拟车道宽度较小时(图3 中的车道2、车道4),按照如下规则合并车道:如果w(k) 图4 车道合并示意 在进行目标车道选择时应满足以下要求:尽可能选择d(k)、w(k)更大的车道;为了保证换道效率及平顺性,防止由于传感器误差造成的航向角突变,希望航向角变化尽可能小,同时目标航向角应尽可能接近当前航向角。根据上述要求,建立车道选择目标函数fs(k),通过最大化fs(k)取值选择合适车道: 式中,hp为上一时刻的航向角命令;hn为当前航向角;D(k)为无碰撞车道选择系数,倾向于在所有虚拟车道中选择无碰撞距离较大的车道;W(k)为车道宽度选择系数,倾向于在所有虚拟车道中选择宽度较宽的车道;Hmin(k)为航向角选择系数,倾向于在所有虚拟车道中选择具有较小的航向角变化值的车道;Hnr(k)为最小航向角变化系数,倾向于在所有虚拟车道中选择更接近车辆当前的航向角的车道;dmax、wmax、hcmax、hdmax分别为最大无碰撞距离、最大车道宽度、最大航向角、最大换道角度,同时使用最大值对fs(k)中的每一项进行限制和归一化;α1、α2、α3、α4分别为目标函数中每一项的权重,其中,α1、α2为正值,α3、α4为负值,为满足上述目标车道选择要求,通过分析不同权重系数下的换道结果,最终选取α1∶α2∶-α3∶-α4=4∶1∶4∶1。 车辆的轨迹可以划分为3个维度展开:车辆纵向加速度(沿道路方向)、车辆横向加速度(与道路垂直方向)、时间。本文根据虚拟车道信息、当前车道平均车速、目标车道平均车速确定换道终点状态,在考虑车辆安全性及乘坐舒适性的前提下,自动规划出满足约束的换道轨迹。 加速换道场景即车辆当前车速小于目标车道平均车速,在换道过程中需要同时进行加速操作。减速换道即车辆当前车速大于目标车道平均车速,换道过程中需要同时进行减速操作。车辆当前车速记为vc,目标车道平均车速vt为: 式中,vt1、vt2分别为目标车道换道终点后方和前方车辆速度。 根据实际道路车辆行驶工况,如果传感器测得的目标车道两车的车速差|vt1-vt2|>5 km/h,说明目标车道辆车可能在进行超车,为保证行驶安全性,则放弃换道超车,继续在本车道行驶。 在研究车辆的换道过程时,由于需要考虑道路环境中其他车辆的运动状态,通常在世界坐标系OwXwYw中创建车辆的全局运动学模型,而研究车辆自身的运动时,一般采用车体坐标系OvXvYv。通常以车辆质心作为车体坐标系原点,如图5所示。 图5 车体坐标系 车辆的运动学方程为: 式中,L为车辆轴距;x(t)、y(t)为车辆质心坐标;(t)、(t)分别为车体坐标系下纵向和横向速度;v(t)为车辆的真实速度;φ(t)为车身横摆角;δ(t)为车辆的前轮转角;θ(t)为车辆航向角。 本文采用五次多项式表示换道轨迹。基于多项式的换道轨迹只需获取车辆的初始状态和终止状态作为边界条件即可求解。基于五次多项式的轨迹计算方法需要3 个维度的边界条件,即车辆的位置、速度、加速度。本文的换道轨迹为: 式中,A0~A5、B0~B5为各项系数;t为时间。 换道起点的边界条件设置为时间t0、车辆起点坐标[x(t0),y(t0)]、速度[(t0),(t0)]、加速度[(t0),(t0)],其中位置、速度、加速度可以通过车载传感器测得。在纵向和横向可以分别得到: 换道终点的边界条件设置为时间t1、车辆终点坐标[x(t1),y(t1)]、速度[(t1),(t1)]、加速度[(t1),(t1) ]。同样,在纵向和横向可以分别得到: 根据车辆的初始状态[x(t0),y(t0),θ0,k0]和目标状态[x(t1),y(t1),θ1,k1],对应的边界条件为: 式中,(x0,y0)、(x1,y1)分别为换道起点和换道终点坐标;(t0)、(t0)分别为换道起点沿x轴和y轴的加速度;(t1)、(t1) 分别为换道终点沿x轴和y轴的加速度;k0、k1分别为换道起点和终点的曲率;θ0、θ1分别为起点和终点的航向角。 在真实交通场景中,总换道时间T的选择需要考虑周边的动态环境,为了保证模型的计算效率,本文没有将T作为自由变量,而是通过换道后的跟驰行为时间tf和换道持续时间tc(tc=t1-t0)的总和决定,即T=tc+tf。结合换道开始时主车运动状态以及其他车辆运行状态进行计算: 式中,vn为换道成功后前车的车速,若换道后的车道没有其他车辆,则vn设置为无穷大。 求解车辆换道轨迹实际上就是求解式(5)和式(6)中的Ai和Bi(i=0,1,2,3,4,5)。在已知车辆换道起点和终点运动参数的前提下,结合式(5)和式(6)即可准确求解式(4)中的参数Ai和Bi。 车辆换道起点和换道终点的选择决定了车辆换道过程的舒适性和安全性,通过对换道参数方程进行分析,对换道结果有影响的参数分别为。根据换道要求,可以得到以下参数: a.换道起点坐标取为(x0,y0)=(0,0); b.换道起点、终点航向角θ0=θ1=0; c.换道起点、终点曲率k0=k1=0; d.横向换道距离y1由虚拟车道生成模块决定。 此问题属于复杂函数在约束下的极小值求解问题,本文采用梯度下降法对函数极小值进行求解。车辆在换道过程中,也会受到轮胎与地面附着力的影响,同时为了保证乘坐舒适性,需对纵向加速度(t)和横向加速度(t)进行限制。限制条件为: 同时,横摆角速度是反映车辆横向稳定性的重要指标,由于车辆正常行驶时的横向速度远小于纵向速度,质心侧偏角约为0,所以车辆的横摆角可以近似使用横向和纵向速度计算,对横摆角求导即可得出横摆角速度。车辆横摆角及横摆角速度的约束为: 为验证算法的可靠性,本文针对不同换道场景进行验证分析。根据实际驾驶中的换道行为,将换道场景分为加速换道和减速换道,车辆在匀速行驶过程中一般不考虑换道行为,所以不考虑匀速换道场景。 设道路总宽度为12 m,满足3 辆车并排行驶需要,目的是可以在虚拟车道生成阶段生成3条虚拟车道,验证本文提出的虚拟车道法车道生成及车道选择的可行性。将换道场景设计为4类:换道至当前车道右侧车道(见图6a)的加速/减速换道场景,换道至当前车道左侧车道(见图6b)的加速、减速换道场景。由于实际行驶中车辆一般为匀速或加速度较小,换道场景中的障碍车辆为匀速运动。4类换道场景如表1所示。 表1 4类换道场景 图6 换道场景示意 场景1 和场景2 中,主车(车辆0)和车辆1 的平均车速小于两相邻车道中车辆2、车辆3 和车辆4、车辆5的平均车速,属于加速换道场景;场景3和场景4中,主车(车辆0)和车辆1的平均车速大于两相邻车道中车辆2、车辆3和车辆4、车辆5的平均车速,属于减速换道场景。 为验证虚拟车道生成以及换道过程的连续性,利用MATLAB 编写脚本文件实现虚拟车道线生成以及换道轨迹规划,并针对不同场景的换道过程进行验证,如图7 所示。从图7 中可以看出,虚拟车道法根据不同的交通状况可以生成不同宽度的虚拟车道,且在换道操作过程无论向左或者向右换道均可根据车辆实际的可通行情况合理选择车道进行换道操作。 图7 不同场景下换道过程仿真结果 通过硬件在环(Hardware-In-the-Loop,HIL)测试对本文提出的换道轨迹规划算法进行验证。基于车辆动力学仿真软件CarSim 搭建仿真场景,将MATLAB 中的车道线生成以及换道轨迹规划程序编译为可执行代码,通过LabVIEW 将期望换道路径的速度、加速度、航向角仿真信号发送至实时仿真机NI-PXI与转向控制硬件平台。转向硬件平台主要由转向盘、转向轴、转向横拉杆、转向电机与转向轴转角传感器等组成。实时仿真机NI-PXI输出的转向盘转角、油门踏板开度等信息分别通过CAN协议发送到相应转向控制器、油门控制器,同时,转向轴转角传感器将采集得到的信号通过板卡发送至NI-PXI 中的仿真模型中。硬件在环测试平台如图8所示,测试流程如图9所示,测试结果如图10 所示。硬件在环测试中,通过本文所述算法生成换道轨迹,并基于线性二次调节器(Linear Quadratic Regulator,LQR)结合车辆运动学模型,对生成轨迹进行跟踪。根据式(3)车辆运动学模型,选取状态量为X=(x,y,φ)T,控制量为U=[,δ]T,则运动学的离散状态空间方程可以表示为: 图8 硬件在环测试平台各组成部分 图9 硬件在环测试流程 图10 加速、减速场景转向盘转角、速度和加速度曲线 生成的参考轨迹上轨迹点i要求的速度;δri为轨迹点i的参考前轮转角;(xri,yri)为轨迹点i的坐标。 轨迹跟踪过程中期望系统的响应过程有如下特点:跟踪误差能够快速收敛到零,并保持稳定;车辆前轮转角δ尽可能小。 针对以上特征,轨迹跟踪问题为典型目标优化最优控制问题,目标函数可以通过对式(12)中累计跟踪偏差X与累计控制输入U进行加权后得出,目标函数J可表示为: 式中,Q、R分别为半正定的状态加权矩阵、正定的控制加权矩阵,需要根据实际控制需求进行选择,通常增大Q可以使跟踪偏差快速趋于零,增大R可以使控制输入尽可能小;N为跟踪过程中的控制点累计数量。 从图10a、图10d 中可以看出,换道轨迹跟踪过程中,车辆转向盘转角变化平缓,换道轨迹平滑,满足车辆在实际行驶过程中的平顺性要求。图10b中,通过速度优化,车辆在减速过程中速度平稳降低,有效避免了换道过程中的顿挫感。图10e中,为了满足换道时的安全性要求,在换道初期车速逐渐降低,换道完成后车辆进行加速,以满足最终速度要求。综上所述,本文提出的虚拟车道法在满足各种车辆约束条件的基础上,可实时自动选择合理车道,并可有效地规划出平顺的换道轨迹。 本文针对车道线不明显或无车道线的交通环境,提出一种虚拟车道生成方法,根据当前道路的交通环境动态生成虚拟车道,并根据车辆自身约束选择合理的可通行车道。在确定行驶车道的基础上,利用多项式生成换道轨迹,并考虑车辆行驶的舒适性和安全性等问题,合理规划换道时的车速,满足车辆实际换道需求。此外,考虑到交通环境的动态性,在一次换道操作执行期间,车辆系统会循环调用本文提出的换道模型更新换道轨迹,直到换道操作完成。 后续在虚拟车道生成以及换道轨迹生成过程中,需对障碍车辆的行为进行预测,结合预测结果生成车道以及换道轨迹,进一步提高车辆行驶的安全性和舒适性。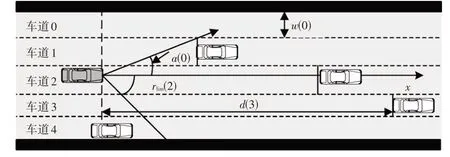
3.3 目标车道选择方法
4 换道轨迹生成
4.1 加/减速换道判断
4.2 车辆运动学模型

4.3 换道轨迹生成
4.4 目标函数约束条件
5 验证分析
5.1 换道场景设计

5.2 仿真验证
5.3 换道场景硬件在环测试


6 结束语
