基于图像处理的三支聚类
2023-11-28管文瑞姜文刚王平心杨习贝
管文瑞,姜文刚,王平心,杨习贝
(江苏科技大学 1.自动化学院;2.理学院;3.计算机学院,江苏 镇江 212100)
聚类是研究样本分类问题的一种统计分析方法,同时也是数据挖掘的一个重要算法。聚类的目的是将数据集划分成多个类簇,使得在同一个类簇中的对象尽可能的相似,不同类簇中的对象不相似。传统聚类算法用一个集合表示一个类,不同的类簇之间有清晰的边界,但在实际划分中常常会遇到信息不充分的情况,如果将数据对象强行划分到某一类簇,会造成误分类的概率增加,导致聚类精度降低。针对传统聚类方法的不足,基于三支决策理论[1],Yu提出了三支聚类的概念[2],其利用三元思想将每个类簇表示为核心域、边缘域和琐碎域[3],使得聚类结果的描述更为合理。一般来说构造三个区域需要阈值,而实际样本中数据的不确定性使得固定阈值划分的区域效果较差。对此,Jia等[4]提出了一种自适应的阈值确定方法,通过核心域与边缘域范围得到Pvi指标,将其最优解作为阈值。一些学者将其优化为无阈值划分方法,如Yu等[5]基于改进DBSCAN的方法得到三支聚类结果。Wang等[6]采用形态学中腐蚀膨胀的思想,将收缩后的区域定为核心域,扩张得到边缘域,克服了固定阈值的局限性。
数字图像处理,是将二维图像表示成数组或矩阵形式,以像素为基本计算单位进行运算。其中将聚类分析的方法在数字图像处理中有着广泛的应用,如基于聚类分析算法的图像分割研究[7];Ali等[8]将数字图像处理的方法反向应用于聚类分析,构建了BS3WC聚类分析算法。本文引入数字图像处理[9]中低通高通滤波器的思想,提出基于数字图像处理的三支聚类方法。使用核密度估计将数据集转化为灰度值,将低通滤波(模糊化)得到稳定的高密度区域定义为核心域,将高通滤波(锐化)得到稳定的低密度区域定义为琐碎域,中间部分则为边缘域。
1 预备知识
1.1 三支聚类
设数据集U={x1,x2,…,xn}包含n个样本对象,传统的聚类方法是用一个集合表示一个类,即寻找一组集合C1,C2,…,Ck满足
式中:k为类簇的个数。上述条件要求一个对象要么属于某个类簇,要么不属于某个类簇,聚类的结果具有清晰的边界,然而,将某些不确定的对象强制分配到某个类中将降低聚类结果的结构和精度。
为了克服传统聚类方法存在的问题,Yu将三支决策[1]的思想引入到聚类中,提出了三支聚类方法[2]。与硬聚类不同的是,三支聚类将数据点与类簇之间的关系分为:确定属于,可能属于以及不属于三类。基于这一思想,三支聚类用Co(Ci)、Fr(Ci)、Tr(Ci)表示一个类,即核心域、边界域和琐碎域,其中Co(C)中的样本点一定属于类C,Fr(C)中的样本可能属于类C,Tr(C)中的对象一定不属于类C。由于琐碎域可通过公式Tr(Ci)=U-Co(Ci)-Fr(Ci)进行表示,三支聚类的结果可以表示为
C={(Co(C1),Fr(C1),(Co(C2),Fr(C2)…,
(Co(Ck),Fr(Ck)}
三支聚类用核心域与边界域来表示一个类,这种聚类方法充分考虑了那些由于信息不充分而无法确定类簇归属的样本对象,降低了决策风险,被广泛应用于属性约简[10]、不确定性分析[11]等领域。
1.2 核密度估计
核密度估计(Kernel density estimation)是根据数据样本的分布情况来获得其总体特征,即为样本的概率密度函数估计,根据概率密度核函数,便可以得到数据分布性质,如数据的聚集区域。常见的密度估计由式(1)给出
(1)
式中:K为非负的单调递减核函数,变量xi和xj为样本点和目标点。V是一组样本。h是用于控制规模的带宽参数,带宽越大所形成的密度曲线越平滑,但会掩盖峰值较小的密度特征。对于核函数K,文献[12]分析说明核函数对密度曲线形态的影响不大。因此带宽是影响曲线的重要参数,一般通过交叉验证法,经验法确定带宽[13]。聚类分析也是通过分析有限的样本数据来得到数据点的特征,将核密度估计作为聚类分析的前处理方法[14],具有良好的可扩展性,对于离群数据或噪声数据不敏感,并且可以对任意形状的数据进行挖掘[15,16]。
1.3 图像处理中的模糊与锐化
模糊(Blurring)运算即低通空间滤波器,在图像处理中用于削减噪声的干扰,并保证图像信息的完整性,又称为图像的平滑[9](Image smoothing)。一般使用的模糊方法有两类:空域法和频域法。空域法是运用模块化运算,提取目标像素点邻域的像素值特性,根据不同的模糊算子进行滤波。频域法是运用正交变换的操作,利用噪声对应的高频信息的特点进行滤波[17]。本文使用空域法进行模糊化操作,空域法又称空间域平滑滤波,常用的方法有均值滤波、高斯滤波和中值滤波等。设输入图像为Uol,模糊化图像为Ubl,模糊运算的定义可表示为
(2)
式中:S为xi邻域像素点的集合,N为S中像素的个数。
对图像Uol所有像素点进行模糊得到模糊图像Ubl。如图1(a)的模糊化操作,高密度数据边缘灰度值会进行衰减,而核心部分不受影响,由此应用于三支聚类,便可以缩减出稳定的核心域Co(Ci)。而边缘区域以及低密度区域灰度值也会进行适当降低,使得图像边缘的涵盖范围适当扩大。

图1 图像模糊锐化处理示例
锐化(Sharpening)运算即高通空间滤波器,在图像中通过定义不同的微分算子,且该算子的响应与灰度的变化幅度相关[9]。因此锐化操作会将灰度图中的边缘区域灰度值提高,而对于衰减信号或低频信号强度降低。本文中锐化操作中添加了模糊化的图像特征[17],设锐化后的图像为Usp,定义锐化运算为
Spf(xi)=f(xi)+k(f(xi)-Lpf(xi))
(3)
式中:k为锐化效果参数,k值越大,低灰度值与高灰度值的分离程度越大,使得低密度区域的数据点更为疏远。对原始图像UOl所有像素点进行锐化得到锐化图像Usp。将该操作映像到三支聚类当中,锐化(高通)滤波器强化了数据集的高密度的边缘区域,并且弱化了数据密度较低的区域,对于离群点(低频信号)进行削减。如图1(c)的锐化操作,高密度与低密度交界处填补为高密度区域,且数据边界不会扩张,因此锐化操作也与数据集三支聚类的期望相符合。
2 基于图像处理的三支聚类算法
2.1 基于核密度估计的二值化图像
根据输入数据集的特征进行采样与量化。采样为决定数字化图像的分辨率,即待处理的聚类分析图像的像素数量。量化是根据核密度估计的方法将各个像素点赋予灰度值。由采样与量化便可以将数据集转换为灰度图像。核密度估计是应用较为广泛的密度测量方法,其定义如公式(1)所示。对于核函数K,本文采用如下的逆多元二次核函数(Inverse multiquadric kernel)[18],表达式如下
(4)
式(4)是一种局部性强的函数,形状为钟形曲线。采用该函数具有两大优势,第一个是模糊系数c为像素框的对角线长度,可以对于不同的数据特征自适应地改变参数,没有需要用户指定的系数,提高了其可用性。第二个是引用其中模糊系数c,避免了低密度区域中的像素(数据之间距离过大)赋予灰度值过低,而高密度区域中的像素赋予的灰度值过高。对于模糊系数c的计算由式(5)给出
(5)
根据逆多元二次核函数可以得到数据点的相对密度.当数据点密度较低时,则分配该点对应的像素点较小的灰度值(一种接近黑色的颜色),当数据点密度较高时,则分配该点对应的像素点较大的灰度值(一种接近白色的颜色)。选取某点附近n个数据点分别计算核函数得到与其对应的密度值,将密度值进行求和并量化至[0,1]区间内。选取的数据点n一般为数据集规模的十分之一。将核函数应用于样本数据集,二维样本数据集特征是均值为100,方差为5的正态分布,可得到灰度值图像如图2所示,可见灰度值图像与三支聚类的语义较为贴切,结构上与三支聚类一一对应,白色像素区域与核心域关联,而外部浅灰色区域与边界域相关联。在下一节中,应用图像处理中的模糊锐化,对图像进行进一步处理。

图2 量化二维数据点图像
2.2 数据图像模糊锐化处理
这一步将对原始的灰度图像进行模糊锐化处理。设低通滤波器(Low pass filter)为Lpf(xi),集合S(f1,…,fm)为像素点f(xi)的邻域像素点,利用式(2)可得原始图像Uol模糊化操作结果。
模糊操作的主要思想是将像素点f(xi)相邻r半径内[19]像素点的均值灰度返回至像素点f(xi),r设置越大,灰度图像模糊化效果就越为平滑。本文中试验结果的领域半径r定为5倍的参数c,即r=5c。如果像素点f(xi)位于高密度边缘,且上方灰度值小于1,进行模糊化使得其灰度值减小,脱离了高密度区域。由此得知进行均值模糊化操作后,数据集中高密度区域进行了缩减,与文献[6]中腐蚀膨胀的方法具有相似之处。
锐化操作将原始图像与模糊图像的差值补充在原始图像中以达到锐化效果,其定义如式(3)所示。锐化操作效果较为自然,避免了锐化边界灰度值突出等问题。图3给出了图像的模糊和锐化效果图,其中(b)为原始图像,(a)与(c)分别为模糊和锐化效果图。
2.3 提取数据特征
锐化也为高通滤波器,可以将其作为聚类分析的前处理方法。锐化操作可以提取锐化后灰度值较高的数据区域,该区域为有效聚类区域,对该区域运行聚类可以有效降低灰度值较低区域对聚类结果的影响。用一个例子来说明这一问题。图4(a)为原始数据图,采用传统聚类方法获得聚类结果图4(c)所示。图4(b)为对原始数据图锐化提取的有效区域,其聚类结果如图4(d)所示。通过对比图4(c)与4(d),发现提取锐化特征后使得聚类对象确,聚类结果有效性提高。

图3 模糊锐化示例图

图4 锐化提取示例图
对锐化提取的有效区域,采用传统聚类算法得到原始的类簇Ck={C1,C2,…,Ck}。为了较好地刻画数据的不确定性,利用模糊与锐化得到每个类的核心域与边界域。由于将原始图像Uol经过模糊化,高密度区域得到缩减,剩下稳定的核心区域,定义该区域为类簇的核心域Co(Ci),表示为
Co(ci)={xi∈U|xi∈Ci∧Lpf(xi)=1}
(6)
模糊操作所提取的特征,说明了该区域模糊前后,像素值始终为1,该情况为目标像素点邻域S(f1,…,fm)全为1,即为稳定的高密度区域。而锐化操作后,图像中高密度区域得到扩展,这意味着扩张部分与核心域关系较为紧密,定义该区域为边界域Fr(Ci),表示为
Fr(ci)={xi∈U|xi∈Ci∧Spf(xi)=
1∧Lpf(xi)≠1}
(7)
该区域经过锐化填补像素值后,扩张为高密度区域,而剩下的部分始终为低密度区域,说明其像素值过小,与核心域联系过于疏远,定义为琐碎域Tr(Ci),表示为
Tr(ci)={xi∈U|xi∈Ci∧Spf(xi)≠1∧pf(xi)≠1}
(8)
通过上述操作,获得了每个类簇的核心域、边界域和琐碎域,其中边界域中数据与该类簇关系紧密,而琐碎域包含了与类簇Ci关系很弱数据,噪声以及离群点等数据。因此琐碎域并不是该类簇的一部分,由此获得将数据集U={x1,x2,…xn}的三支聚类结果
C={(Co(C1),Fr(C1)),(Co(C2),Fr(C2))
…,(Co(Ck),Fr(Ck))}
(9)
2.4 基于图像处理的三支聚类(3WDIP)算法流程
基于图像处理的三支聚类算法基本思想是采用数字图像处理中模糊与锐化的思想提取数据集中的特征,即对原始数据进行核密度估计,使得二维数据可以生成可视化灰度图像,高维数据仅得到数据点处灰度值。首先对数据总体采用模糊与锐化操作,得到总体数据特征,即稳定的高密度区域以及稳定的低密度区域。提取锐化后灰度值较高的数据区域,将低密度区域从原始数据中删除。对灰度值较高的数据采用传统的聚类算法得到不同的类簇,这样可以有效降低灰度值较低区域对聚类结果的影响。为了较好地刻画数据的不确定性,本文利用对每个类簇进行模糊与锐化得到每个类的核心域与边界域,由此获得将数据集的三支聚类结果。算法1给出了基于图像处理的三支聚类(3WDIP)算法过程。
2267048036002

算法13WDIP算法

输入:数据集U,簇数目k,领域半径r.
输出:C={(Co(C1),Fr(C1)),(Co(C2),Fr(C2))…,(Co(Ck),Fr(Ck))}
步骤1 根据数据集规模采样,并得到核函数中参数c。
步骤2 使用核密度估计进行量化得到原始灰度数据Uo。
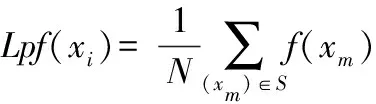
步骤4 根据原始灰度数据Uo和模糊灰度Ubl得到锐化灰度Usp。
步骤5 对锐化提取区域数据进行聚类得到原始聚类结果Ci(本文分别采用k-means与DPC)。
步骤6 提取Co(ci)={xi∈U|xi∈Ci∧Lpf(m,n)=1},得到Ci的核心域。
步骤7 提取Fr(ci)={xi∈U|xi∈Ci∧Spf(m,n)=1∧Lpf(m,n)≠1},得到Ci的边界域。
步骤8 得到最终聚类结果:C={(Co(C1),Fr(C1)),(Co(C2),Fr(C2))…,(Co(Ck),Fr(Ck))}

3 试验分析
为了对本文算法的有效性进行验证,本文选取了12组UCI数据集进行试验。数据集信息如表1所示,其中部分数据添加了噪声数据。

表1 试验所用数据集UCI
首先对原始数据进行核密度估计,得到数据点处灰度值,然后对数据集进行模糊和锐化操作。提取锐化后的高密度区域,采用k-means获得硬聚类结果,然后对每个类簇进行模糊与锐化得到每个类的核心域与边界域,由此获得将数据集的三支聚类结果并计算聚类指标调整兰德系数ARI,标准化互信息NMI,调整互信息AMI。ARI的范围为[-1,1],值越大意味着聚类结果与真实情况越吻合,NMI与AMI指标值域为[0,1],值越大两个聚类结果的相近程度越接近。试验结果如表2所示。为了对比本文算法的效果,表2还给出了UCI数据集用k-means聚类的结果。

表2 3WDIP嵌入k-means试验结果
将对应数据的均值相差,得到指标差值对比图5。图中负值表示使用3WDIP后聚类效果下降。
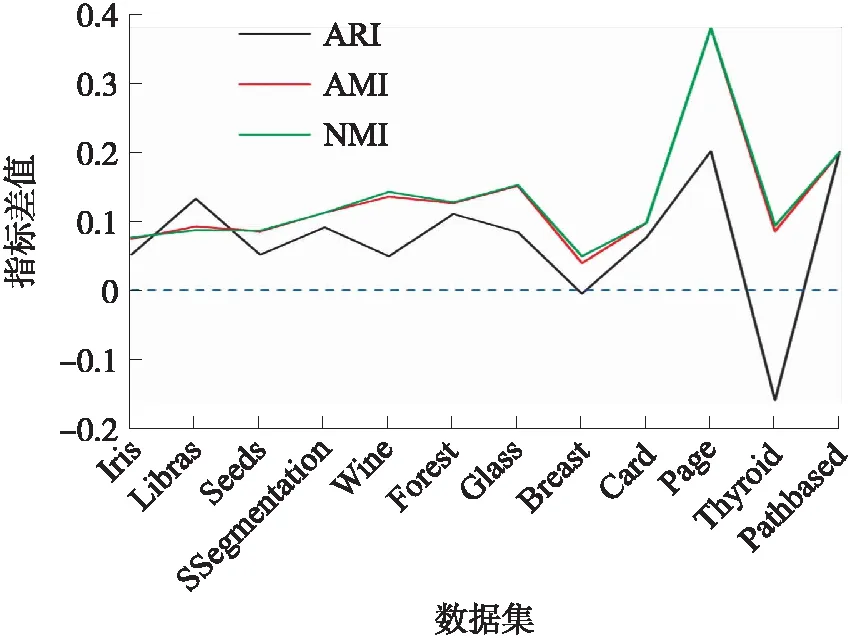
图5 聚类指标差值图
为了进一步验证算法的有效性,对上述数据集锐化提取的高密度区域,使用DPC聚类获得硬聚类结果,然后对每个类簇进行模糊与锐化得到每个类的核心域与边界域。图6为使用3WDIP嵌入DPC后得到的聚类结果与直接采用DPC算法得到的聚类结果在ARI、NMI和AMI上的对比图。
观察表2和图6的对比试验数据,可得出以下结论:
(1)通过对比NMI标准互信息发现,3WDIP算法应用于K-means时,各项数值增幅较为稳定。其中数据集Page在运用了3WDIP算法后,ARI和NMI的值为0.2856和0.4939,而仅运行K-means的两个数值为0.060 1和0.116 6。这种改进归因于锐化提取中消除了噪音以及离群点的干扰,仅对核心域和边界域进行聚类,明确了各个类簇之间的边界。
(2)将其应用于DPC算法时,各项数值平均增幅比K-means要高,这归因于3WDIP算法中模糊与锐化处理。灰度值与DPC中密度值意义相关联,在经过模糊锐化,各个类簇的边界域和核心域的灰度值得到补充,而琐碎域的灰度值得到下沉,使得类簇与外部之间关联性降低,提高了类内的聚集程度。而数据集Breast未能得到改进,是由于类簇内部数据分布不均,数据内部存在鞍点,使得3WDIP降低了鞍点左右的灰度值,导致其应用于DPC时效果不佳,而在K-means中稳定发挥。
综上所述,3WDIP算法能较好地对数据特征进行处理,能应用于不同的聚类方式,并且能较为稳定的提升聚类性能,其三支聚类结果可解决现实中不确定性的聚类问题。
4 结论
本文将数字图像处理中模糊与锐化的思想与三支聚类进行结合,给出了一种基于图像处理的三支聚类算法。这算法通过提取锐化后灰度值较高的数据区域,对灰度值较高的数据采用传统的聚类算法得到不同的类簇,然后对每个类簇利用图像模糊算子得到类簇的核心域,锐化算子得到类簇数据边界域,从而获得每个类簇的三支表示。试验结果表明,本文的算法将核心域和边界域突出显示,提高了各个类簇之间的分离程度,使得各项聚类性能稳定的增加。这算法仍存在需要改进的地方,如应对类簇内部数据分散不均而产生的鞍点,3WDIP算法会对这区域进行削弱,这种错判使得类内分散性提高。此外,在模糊化操作中,虽然引用了自适应的可达半径进行模糊操作,还需丰富评价模糊化所需数据参数,如何进一步提取数据特征进行优化也是下一步的研究工作之一。
