三维后期重建中基于果蝇优化的点云数据配准研究

王 婷,李 凯,张 洁,杨雨佳

(1.徐州工业职业技术学院 建筑工程学院,江苏 徐州 221140;2.中国矿业大学 环境与测绘学院,江苏 徐州 221116; 3.中国矿业大学 力学与土木工程学院,江苏 徐州 221116;4.广州理工学院 计算机科学与工程学院,广东 广州 510540)

点云配准作为三维重建技术的关键步骤,配准性能直接影响三维重建效果,在艺术表达、室内装饰设计等领域具有广泛的应用。三维重建需要通过图像采集设备从不同角度获取重建对象的完整数据,这些数据构成了点云。虽然这些点云数据都是重建对象的特征数据,但是由于拍摄角度及环境等原因,这些数据也呈现着较大差异。

点云配准技术通过坐标转换及平移操作,将不同角度点云进行映射[1],最后得到完整的重构对象。点云配准根据源点云和目标点云的距离最小值优化来进行配准参数求解[2]。由于点云规模和旋转平移复杂度影响,点云配准的精度和效率可能受到影响,而且在采集点云数据,由于受到噪声影响和离群点的干扰,这给后期的点云配准及三维重建带来更大挑战。

近年来,基于智能算法的点云配准方案是研究热点。根据源点云和目标点云的距离值构建目标函数,通过算法优化目标函数,得到点云配准的关键参数。例如,张顺利等[3]采用尺度迭代最近点(Iterative closest point,ICP)方法实现点云配准,并采用自适应邻域算法对局部曲面形状的关键参数进行优化,有效提高了真实匹配点对的配准成功率;闫利等[4]采用ICP进行局部优化,并借助遗传算法进行全局优化,获得了较高的Hausdorff性能指标。这两个研究都是在基础ICP的算法上进行不同程度的改进,但是其配准精度仍不理想,此外没有从旋转均方根误差和平移均方根误差等指标进行全面的性能测试。

不同于遗传算法和邻域算法,果蝇优化算法(Fruit-fly optimization algorithm,FOA)算法则是基于果蝇的行为模式进行开发的。FOA采用基本的随机搜索策略,易于实现和优化。遗传算法的核心是通过交叉和变异来生成新个体,并不断演化,而FOA则是通过随机性飞行来扩大搜索空间。FOA可以在较宽范围内随机地搜索解空间。FOA适用于解决大规模、多峰、复杂问题,而这些正符合点云配准应用的特点。

因此,本文采用FOA用于点云配准,通过果蝇的气味搜索功能来实现配准目标函数优化求解。同时,FOA可以通过引入动态权重的策略来实现更好的搜索结果,从而获得较低的配准误差,且配准效率高。

1 点云数据数据变换配准

1.1 点云的旋转和平移

设三维空间中的一点a(x,y,z)经过坐标变换后a′(x′,y′,z′),Rx(α)为xyz到xy′z′的变换矩阵,那么有

(1)

而Ry(β)为xyz到x′yz′的变换矩阵,满足条件

(2)

Rz(γ)为xyz到x′y′z的变换矩阵,满足条件

(3)

那么点云集中的某一点坐标a(x,y,z)需要变换至a′(x′,y′,z′),计算方法为

R=Rx(α)·Ry(β)·Rz(γ)

(4)

在点云位置变化过程中,平移变化是一种不改变相对位置的距离变化,设B(x,y,z)点平移至B′(x′,y′,z′)的变化公式为

(5)

将该公式转化为矩阵表示,则

(6)

那么点云同时经过旋转和平移可得[5]

(7)

式中:t为平移向量,点云配准就是为了实现不同角度的坐标对齐,而R和t是2个关键变量,是配准研究需要终点解决的问题。

1.2 点云配准

设2个点云S∈{xi∈R3|i=1,2,…,N}和T∈{yj∈R3|j=1,2,…,N},S为源点云,T为模板云,xi和yj分别为这2个点云里的点,那么点云配准的目标函数为[6]

(8)

在配准评价时,R和t的误差常作为配准精度的重要评价方式。除此之外,源点云和模板点云之间的Hausdorff距离也是常用配准评价方式之一,下面将对Hausdorff距离计算方法进行描述。设2个点云S1和S2,S1至S2的Hausdorff距离

(9)

式中:d(a,b)表示点a与b的欧式距离。

S2至S1的Hausdorff距离为

(10)

Hausdorff双向距离为

H(S1,S2)=max{h(S1,S2),h(S2,S1)}

(11)

2 基于果蝇优化算法的点云配准

2.1 果蝇优化算法

设果蝇群体的初始位置为Xinit、Yinit,群内个体随机运动后的位置变为[7]

Xi=Xinit+Hr

(12)

Yi=Yinit+Hr

(13)

式中:Hr表示[-H,H]的任意值,一般选择方法为[8]

Hr=H×[2×rand()-1]

(14)

式中:H表示FOA个体最大移动步长。

设某个体(Xi,Yi)距离原点为d

(15)

Si=1/d

(16)

则该个体的味道浓度定义为[9]

Smelli=Function(Si)

(17)

式中:Function为适应度函数[10]。

找出Smelli的最佳值bestSmelli及对应坐标Xbest、Ybest。接着将Xbest、Ybest作为最新的Xinit、Yinit,重复执行式(12)～(17),不断更新bestSmelli。

在果蝇的最优值搜索时,H值对寻优精度与效率均有影响,若H值设置不合理,FOA的优化适应度将快速下降。因此,为了防止人为设置不合理,考虑采用自适应设置方式,将H值得变化与味道浓度变化率R绑定,设定R范围为[Rmin,Rmax]。

R计算方法[11]

(18)

式中:δ表示正向趋于0的值。

若R∉[Rmin,Rmax],则H的更新迭代方法为[12]

(19)

若R∈[Rmin,Rmax],则[13]

(20)

式中:G和Gmax分别为当前迭代次数和最大迭代次数。将式(12)和(13)中的Hr替换为Hi。

2.2 点云配准流程

首先,获得源点云样本特征,并结合目标点云构建配准目标函数,接着构建FOA的点云配准模型,以配准目标函数作为FOA适应度函数,以FOA的气味浓度最优值搜索完成点云配准旋转和平移向量的寻优,其主要流程如图1所示。

图1 基于FOA的点云配准流程

3 实例仿真

为了验证FOA算法的点云配准性能,分别对表1中的4类点云样本集进行配准仿真。首先采用FOA算法对点云样本进行配准及可视化仿真,其次分别在点云集中加入不同强度噪声和不同离散群比例,验证FOA的配准性能,最后采用不同配准算法和FOA配准进行性能对比。

表1 点云集

3.1 FOA的配准性能

采用FOA对4类点云集进行配准性能仿真,其配置主要性能指标如表2所示。

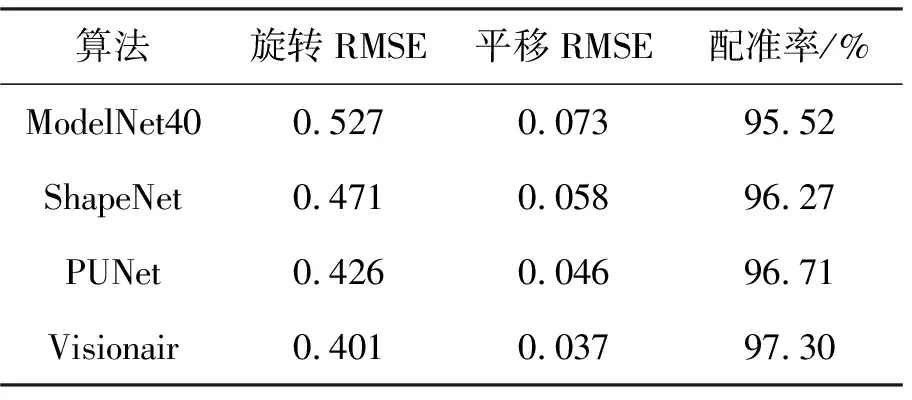
表2 FOA的配准性能

从表2知,对于4类点云集,FOA均表现出了较高配准性能,其旋转RMSE最大值不超过0.53,而平移RMSE保持在0.08范围内,配准率均高于95%。横向对比发现,FOA 对Visionair集的配准适应度最高,ModelNet40集最低,这可能是由于样本本身的点云结构复杂度决定的。

图2展示了2个点云样本配准的可视化结果,源点云(绿色)相对于模板点云(白色)配准后的结果(红色)重叠度高,这说明FOA算法的配准效果好。

图2 点云配准可视化

3.2 不同环境下的配准性能

为了验证三维重建复杂环境下的FOA的点云数据配准的稳定性,首先在原点云数据样本中加入高斯噪声,验证不同噪声强度下的FOA配准性能。其次,在源点云和目标点云集中加入等量干扰离群值,验证不同规模离群值下的FOA配准性能。

3.2.1 不同噪声环境下的配准性能

在点云样本中加入N(0,σ)的高斯噪声,σ差异化选择0.1%、0.5%、1%、1.5%和2%,其不同噪声强度下的配准性能如表3所示。

从表3知,噪声对FOA的点云配准影响较大,噪声强度与配准性能呈反比。对比噪声强度最低和最高的两组数据,ModelNet40、ShapeNet、PUNet和Visionair集的旋转误差分别增大了92.39%、99.55%、75.98%和64.81%;ModelNet40、ShapeNet、PUNet和Visionair集的平移误差分别增大了117.2%、132.25%、145.45%和178.57%;在配准率方面,ModelNet40、ShapeNet、PUNet和Visionair集分别下降了4.58%、4.40%、4.63%和2.07%,横向对比Visionair集的旋转误差受到噪声的影响相比其他3类集更小,ModelNet40集的旋转误差受到噪声影响最大,但平移误差受到噪声却最小。在配准率方面,ModelNet40集受到噪声的影响下降最快,Visionair集下降得最慢。

表3 不同噪声强度下的FOA配准性能

3.2.2 不同离群率情况下的配准性能

在不加噪声,仅加入离群值得情况下,验证FOA的配准性能,差异化加入离群值比例(占所有点云量百分比),其配准性能如图3和图4所示。

从图3可以看出,对于4类点云集,在离群值比例从0增至90%时,其旋转RMSE均在缓慢上升,其中变化最大的ModelNet40集从离群值比例0增至90%时,RMSE仅增加了15.78%,这说明FOA对多点云环境下的目标点云针对性配准稳定性高。

图3 不同离散群比例的旋转RMSE

图4 不同离散群比例的平移RMSE

从图4得,4类点云集的配准平移RMSE值对离群值比例并不敏感,只有ModelNet40集和PUNet集的RMSE有较小的提升,ShapeNet和Visionair集的平移RMSE基本没有变化,这说明FOA的点云配准的平移误差基本不受离散群加入的干扰。

3.3 不同算法的配准性能

分别采用ICP算法、DE-GWO算法、DGCNN算法和FOA算法对表1中的4类样本集进行配准性能仿真,其配准性能如表4～7所示。

表4 4种算法的配准性能(ModelNet40集)

表5 4种算法的配准性能(ShapeNet集)

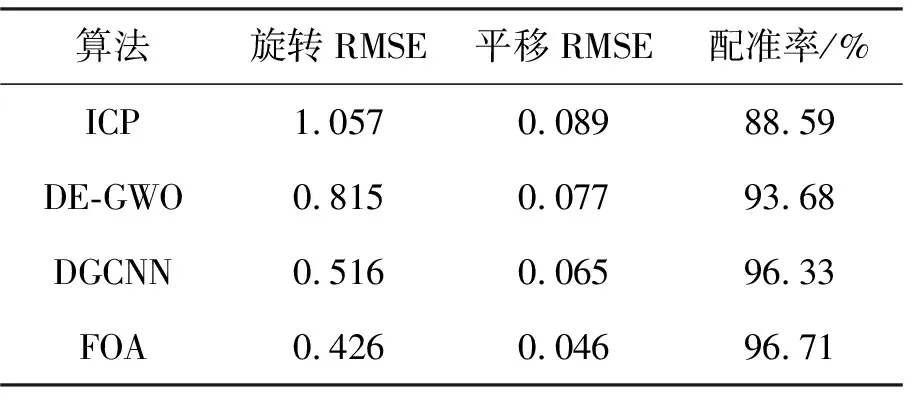
表6 4种算法的配准性能(PUNet集)

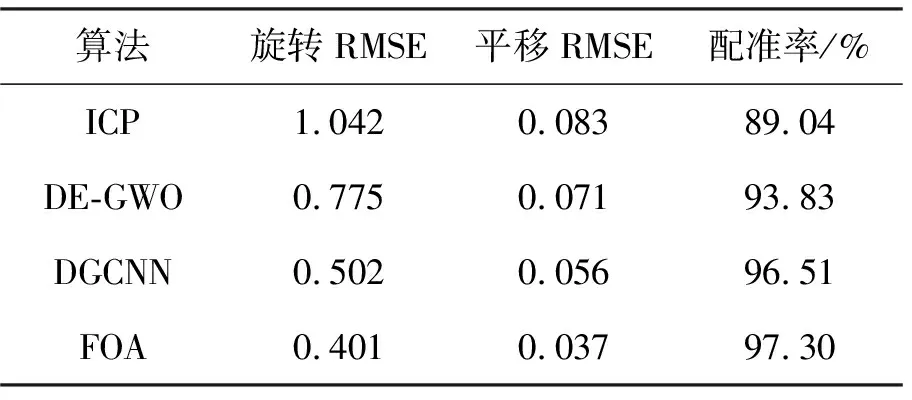
表7 4种算法的配准性能(Visionair集)

从表4～7可得,对于4类点云集,FOA的点云配准性能最高,DGCNN略低,ICP较差。在ModelNet40集,FOA和DGCNN的平移RMSE分别为0.073和0.075,配准率分别为95.52%和95.31%,两者配准性能非常接近,而在其他3类点云集,两者有一定差距。

4 结束语

本文采用FOA用于点云配准目标函数的优化求解。通过设置自适应搜索步长,FOA算法对三维重建的点云配准实现较高的配准成功率,且相比常用配准算法,能够获得更优的旋转和平移RMSE性能。在应对噪声和离群值干扰时,FOA仍能表现较高的配准性能。后续研究将对FOA进行改进,并结合注意力机制对大规模点云进行重建对象特征的有效提取,以增强FOA应对噪声干扰的配准可靠性,提高FOA算法在点云配准中的适应度。