重型燃气轮机高雷诺数CDA叶型转捩特性数值计算
2023-11-27王润禾羌晓青杜朝辉欧阳华
王润禾 ,童 歆 ,羌晓青 ,杜朝辉 ,3,欧阳华 ,3
(上海交通大学机械与动力工程学院1,航空航天学院2:上海 200240;3.燃气轮机与民用航空发动机教育部工程研究中心,上海 201306)
0 引言
重型燃气轮机是驱动和发电系统的核心设备[1],其3 大核心部件之一燃气轮机压气机的气动性能与燃机整机的性能密切相关。重型燃机压气机具有高雷诺数、高湍流度的流动特点,在运行过程中,压气机内的弦长雷诺数为2×106~6×106[2]。在压气机叶栅通道内,气流在不同进口雷诺数条件下呈层流、转捩流或湍流等流态,对叶栅的气动性能产生不同的影响[3]。因此,深入探究压气机内部的流动机理是压气机设计的基本要求,也是提高压气机设计水平的重要手段。
20世纪30-40年代,国外研究人员发现了雷诺数对压气机性能存在一定的影响。1968年,Wassell[4]发现随着雷诺数的改变,压气机的压比与效率特性曲线发生位移;1999 年,Köller 等[5-6]对设计叶型的性能进行了试验验证,并对该叶型高雷诺数下的转捩特性进行了观测;2020 年,Holley 等[7]通过试验发现,在Re=1.95×106~3.25×106时,随着雷诺数的降低转捩向下游移动。同时,中国的诸多学者为此也进行了很多相关研究与分析。赵峰等[8]、王名扬等[9]和郭捷等[10]发现随着雷诺数的降低,叶片损失增大;雷志军等[11]采用表面热膜测试技术,系统地研究了在不同雷诺数条件下叶片吸力面边界层的自由转捩过程。说明雷诺数对叶片气动性能有一定影响,尤其对叶片附面层流动具有设计要求的叶型,如可控扩散叶型(Controlled diffusion airfoil,CDA)。CDA叶型是由20世纪70年代机翼的超临界翼型发展而来,其压力分布符合“Stratford 分布”[12]。该压力分布形式使其吸力面前缘附近的气体加速至最大马赫数以提供有利的压力梯度来保证层流边界层不发生分离,在压力面设计的气体流速基本保持不变以保持层流边界层。气流从层流流动到湍流的转捩,直接决定了CDA 的气动性能。上世纪,Emmons[13]、Mayle 等[14]通过理论描述转捩的发展过程;2017 年,王文涛[15]分析了进口来流湍流度和雷诺数变化对某CDA 叶片表面层流分离、转捩以及角区分离的影响。但在高雷诺数下,雷诺数变化对转捩影响的研究较为有限。叶片表面的摩擦阻力系数是边界层流态的一种体现。层流边界层扰动很小,流线紧贴壁面,因此其摩擦阻力系数比较小。扰动逐渐增大,流线不再紧贴壁面,气流的混乱程度增大,因此湍流边界层的摩擦阻力系数比层流边界层的大[16]。可以利用这一特性区分并判断层流边界层和湍流边界层[14]。边界层从层流转为湍流的过程中,摩擦阻力系数在转捩点先增大,然后再减小[17]。由于层流边界层的摩擦阻力小于湍流边界层的,因此推迟CDA 叶型吸力面层流向湍流过渡的转捩点的位置以获得更小的流动阻力。
本文针对高雷诺数对CDA 叶型气动性能及流动的影响,基于耦合转捩模型的雷诺时均方程对某CDA叶型进行了数值计算。
1 研究对象与数值计算方法
本文采用商用软件ANSYS CFX,通过求解雷诺时均N-S 方程,对某工业级压气机叶片50%叶高处CDA叶型进行数值模拟,CDA叶型的几何参数见表1。湍流模型采用k-ωSST(shear stress transport)模型,因为SST 湍流模型是两方程模型,其在近壁面保留了原始的k-ω模型方程,在远离壁面的充分发展区使用k-ε模型方程求解,运用混合因子将二者有机统一,尤其适合于对边界层模拟精度较高的情况。转捩模型采用G-T(Gamma-Theta)模型捕捉流动中的转捩过程。G-T 转捩模型由控制间歇因子γ和当地转捩动量厚度雷诺数的2个输运方程构成

表1 CDA叶型的几何参数
其中
式中:S为应变率的模;Ω为涡量的模;Flength为转捩区的长度,其为经验关联函数,是转捩动量厚度雷诺数的函数;Pθt为源项,设计目的是使边界层以外的;λt为时间尺度;Fθt为混合函数,用来消除边界层内的生成项Pθt。
选择理想气体为计算工质,采用高精度的对流形式,进口湍流度设置为5%,叶高方向设置为对称性(symmetric)边界条件,叶片交界面设定为平移周期边界,用以模拟多个叶片并列分布,减少总体计算量。稳态计算的收敛标准设置为通量残差的均方根值<1×10-6。
在仿真计算中采用HOH型拓扑网格,如图1所示。叶片壁面的网格膨胀比设为1.1,保证壁面上y+<1,满足湍流模型与转捩模型对边界层网格的要求。考虑到网格质量对计算湍流和转捩过程的重要性,本文通过对比5 种不同规模的网格进行了网格无关性验证。不同规模网格参数见表2。全攻角动压损失系数的特性对比计算结果如图2 所示。其中总压损失系为

图1 2维计算网格

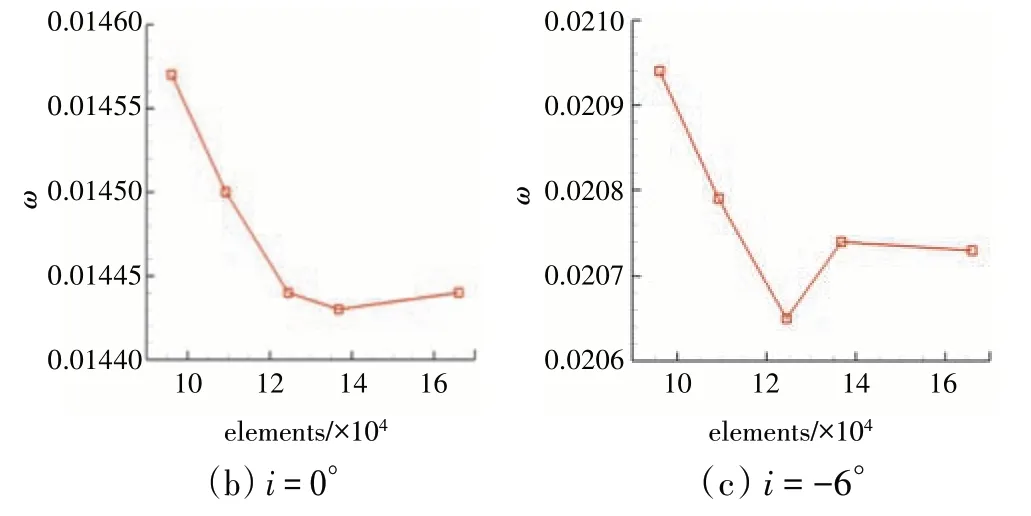
图2 不同网格下动压损失系数-攻角特性对比

表2 不同规模网格参数
式中:Pt0为叶栅的进口总压;Pt1为叶栅的出口总压;P0为叶栅的进口静压。
由于在更大网格数下,当叶片在负攻角工况下计算时收敛性不好,易出现非定常波动,且在设计点、正攻角工况下,叶片数值计算既能保证网格无关性,又能减少计算规模。因此,本文最终选取网格数为124521 进行计算。
为验证数值计算方法的准确性,用3 维仿真计算的结果与试验结果对比。在平面叶栅吹风试验中,在叶片压力面和吸力面各布置了16 个静压探孔,用以测定叶片表面的静压分布。在Re=5.0×105、攻角i=0°工况下试验测量得到的静压分布与数值计算结果的对比如图3 所示。其中叶表位置X通过叶长C进行无量纲化。纵坐标P*为压力系数

图3 叶片表面的静压分布与数值计算结果的对比
式中:P为叶片表面静压。数值模拟设定的边界条件与试验相同。
从图中可见,本文采用的数值计算设置得到的结果与试验数据在总体上吻合很好。
1.1 不控制马赫数
在保持出口背压为环境压力不变的情况下,在不控制马赫数条件下,通过改变进口总压与进口总温来调整工况雷诺数,如图4所示。从图中可见,随着雷诺数的增大,总压损失系数增大,且可用攻角范围急剧减小。当Re=9.0×105、1.0×106时,进口马赫数已超过0.8,再增大雷诺数,进口马赫数将超出亚临界声速范围。
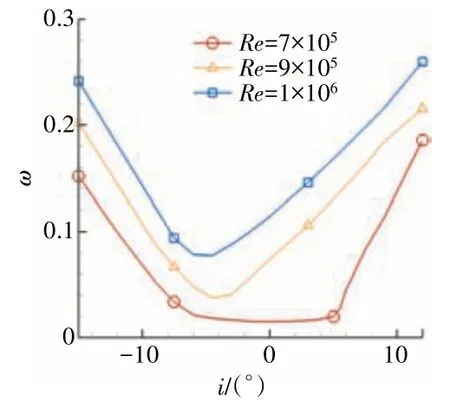
图4 在不控制马赫数条件下,叶片总压损失系数随雷诺数的变化
1.2 控制马赫数
在平面叶栅试验研究中,因为试验条件的限制无法控制背压和对进口流体流态进行调控。然而在实际工作中当雷诺数增大时,流体速度不会随着线性增大而迅速达到超声速,而是受前后级与其他部件的限制使工质的温度、密度产生显著变化。与不控制马赫数的工况对比,我们研究了控制马赫数时高雷诺数对压气机叶片气动性能的影响。
为研究高雷诺数对压气机叶片的影响,分析了在Ma=0.6 条件下,当Re= 8.2×105、9.8×105、1.09×106、1.17×106、5.0×106和1.0×107时压气机叶片的气动性能,如图5 所示。从图中可见,当控制马赫数时,随雷诺数的增大,总压损失系数减小,且最小总压损失系数向正攻角方向偏移,可用攻角范围基本不变。
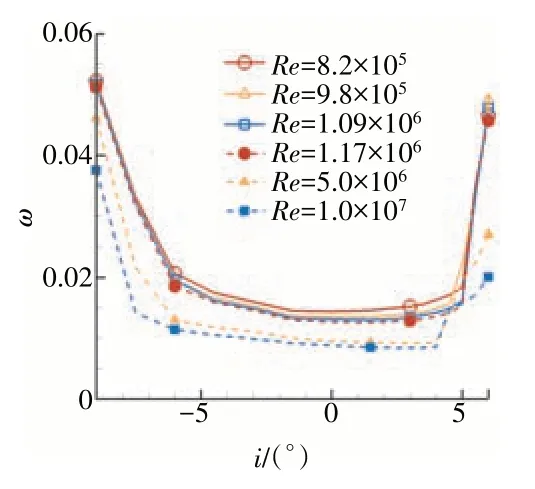
图5 在控制马赫数条件下,叶片总压损失系数随雷诺数的变化
2 结果分析与讨论
2.1 总压损失分析
在不控制马赫数条件下,当i= 0°时总压损失系数随雷诺数的变化如图6 所示。从图中可见,总压损失系数随雷诺数的增大而增大,当Re=7×105~9×105时,总压损失系数增加了约391.95%,而将Re=9×105与Re=1×106的计算结果进行比较,总压损失增大了约54.22%。在控制马赫数条件下,当i=0°时总压损失系数随雷诺数的变化如图7 所示。从图中可见,总压损失系数随雷诺数的增大反而减小,当Re=106~5×106时,总压损失降幅明显。将Re=8.2×105与Re=5×106的计算结果进行比较,总压损失降低了约33.93%,而将Re= 5×106与Re= 1×107的计算结果进行比较,总压损失降低了约7.65%。
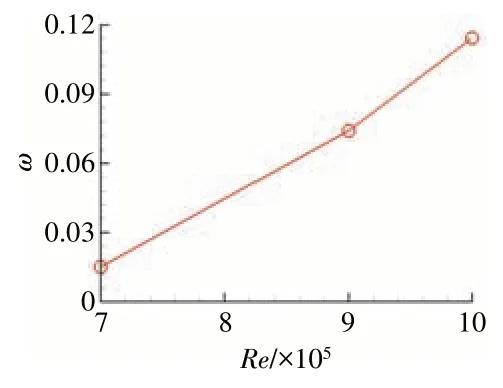
图6 在不控制马赫数条件下,当i = 0°时总压损失系数随雷诺数的变化

图7 在控制马赫数条件下,当i = 0°时总压损失系数随雷诺数的变化
2.2 对转捩的影响
当Ma=0.6、i=0°时转捩位置随雷诺数的变化如图8 所示。当Re= 8.2×105叶片转捩位置位于42.8%弦长附近,而当Re=5.0×106、1.0×107时叶片的转捩位置前移至36.0%、34.0%弦长处。将Re= 8.2×105与Re= 5×106的计算结果进行比较,转捩位置前移约15.89%,而将Re=5×106与Re= 1×107的计算结果进行比较,转捩位置前移约5.56%。从图中可见,随雷诺数增大,叶片转捩位置前移,但转捩起始位置前移的速度减缓。

图8 当Ma = 0.6、i = 0°时转捩位置随雷诺数的变化
在不控制马赫数条件下,当攻角i= 0°,Re= 7×105、9×105和1.0×106时的叶片吸力面及其中部表面摩擦系数Cf沿弦长方向分布如图9 所示。从图中可见,当Re= 7×105时的吸力面转捩点位于约42.8%弦长处。在Re= 9×105、1.0×106下的叶片吸力面约在25% ~35%弦长处,表面摩擦系数Cf骤降,在50%弦长后出现轻微波动,未出现发生在转捩时相应的Cf走势改变。
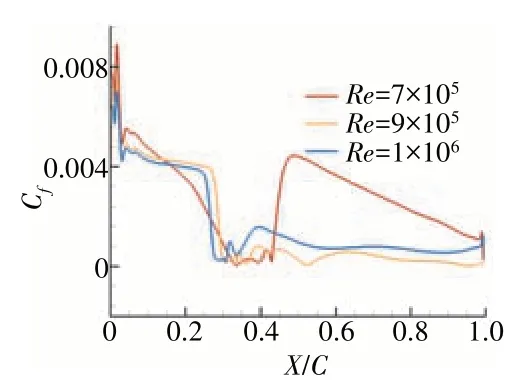
图9 在不控制马赫数条件下,当i = 0°时的吸力面时均Cf分布
当攻角i=0°、Ma=0.6 时,在Re=8.2×105、1.17×106、5.0×106和1.0×107下的叶片吸力面及其中部表面摩擦系数Cf沿弦长方向分布如图10(a)(b)所示。从图中可见当Ma= 0.6 时,在Re= 8.2×105、1.17×106、5.0×106和1.0×107时的吸力面转捩点分别位于约42.8%、41.1%、36.0%、34.0%弦长处。将Re=8.2×105与Re=5×106的计算结果进行比较,转捩位置前移约15.89%,而将Re= 5×106与Re= 1×107的计算结果进行比较,转捩位置前移约5.56%。
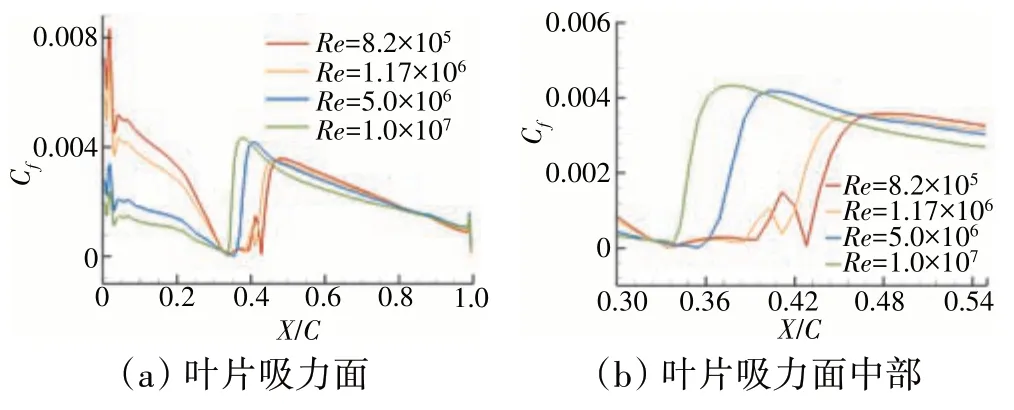
图10 在Ma = 0.6、i = 0°的时均Cf分布
在不控制马赫数条件下,攻角i= 6°时,在Re=7×105、9×105和1.0×106下的叶片吸力面及其前缘表面摩擦系数Cf沿弦长方向分布如图11 所示。从图中可见,当不控制马赫数时,在Re= 7×105的吸力面转捩点位于约4.43%弦长处。在Re= 9×105、1.0×106下的叶片吸力面在近20%弦长处表面摩擦系数Cf骤降,随后产生1个小峰。
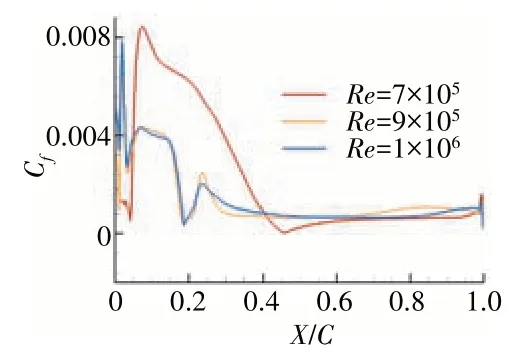
图11 在不控制马赫数条件下,当i = 6°时的吸力面时均Cf分布
当Ma=0.6、攻角i=6°时,在Re=8.2×105、1.17×106、5.0×106和1.0×107下的叶片吸力面及其中部表面摩擦系数Cf沿弦长方向分布如图12(a)(b)所示。从图中可见,当Ma= 0.6 时,在Re= 8.2×105、1.17×106、5.0×106和1.0×107的吸力面转捩点分别位于约4.78%、3.54%、1.23%、1.11%弦长处。将Re=8.2×105与Re=5×106的计算结果进行比较,转捩位置前移约74.3%,而将Re=5×106与Re=1×107的计算结果进行比较,转捩位置前移约9.8%。

图12 在Ma = 0.6、i = 6°时的时均Cf分布
在不控制马赫数条件下,当攻角i= -6°时,在Re=7×105、9×105和1.0×106下的叶片吸力面及其中部表面摩擦系数Cf沿弦长方向分布如图13 所示。从图中可见,当不控制马赫数时,在Re= 7×105、9×105和1.0×106下的吸力面转捩点分别位于约53.1%、50.0%、42.0%弦长处。将Re= 7×105与Re= 9×105的计算结果进行比较,转捩位置前移约5.8%,而将Re= 9×105与Re= 1×106的计算结果进行比较,转捩位置前移约16.0%。

图13 在不控制马赫数条件下,当i = -6°时的吸力面时均Cf分布
在攻角i= -6°、Ma= 0.6 时,在Re= 8.2×105、1.17×106、5.0×106和1.0×107下的叶片吸力面及其中部表面摩擦系数Cf沿弦长方向分布如图14(a)、(b)所示。从图中可见,当Ma= 0.6 时,在Re= 8.2×105、1.17×106、5.0×106和1.0×107下的吸力面转捩点分别位于52.3%、49.2%、、42.8%、41.1% 弦长处。将Re=8.2×105与Re=5×106的计算结果进行比较,转捩位置前移约18.2%,而将Re=5×106与Re=1×107的计算结果进行比较,转捩位置前移约4.0%。

图14 在Ma=0.6、i=-6°时的时均Cf分布
当i=-6°、0°、6°时,叶片吸力面转捩位置随雷诺数变化数据见表3。
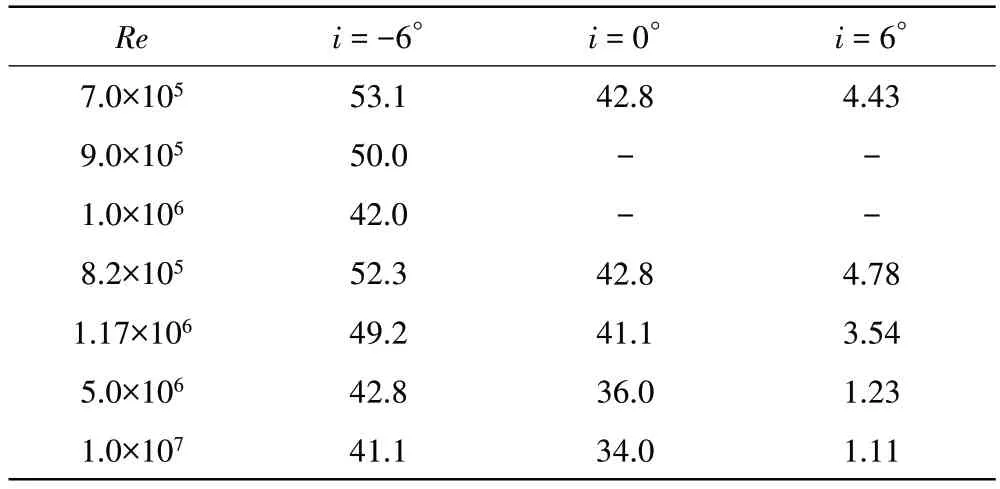
表3 叶片吸力面转捩位置随雷诺数变化 %
2.3 在i=0°叶片表面压力分布的对比
当Re=7×105时,在吸力面约为40%~50%弦长处出现了1 个阶跃型的波动同时发生了流动分离如图15(a)所示。从图中可见,在分离点前,叶片表面为层流流动,流动的扰动很小,压力变化梯度较小。在气体从叶型前缘往后缘流动过程中,气体在顺压梯度作用下保持层流流动;在分离点附近时,逆压梯度增大,气体受逆压梯度的影响产生较大的垂直于壁面的分速度,使扰动不断扩大,导致气体不再紧贴壁面,开始产生分离流动。由气体分离带来的扰动,促使边界层的流动从层流状态迅速转变为湍流,即发生了转捩。在叶片的压力面,压力系数曲线几乎接近水平,说明在压力面,气体的压力基本没有变化,气体的流动保持层流的状态,流线紧贴壁面没有发生分离。

图15 在不控制马赫数条件下,i=0°的P*分布
当Re=1×106时(见图15(b)),相比Re=7×105时叶片压力系数在前20%弦长处下降迅速,在约为20%~40%弦长处,吸力面出现了1个比较大的转折,与图9吸力面时均Cf在20%~40%弦长处发生的变化一致。之后吸力面压力系数增大,但仅增大至约0.6,叶片吸力面的流动损失显著。在叶片的压力面,压力系数在前10%弦长处发生了陡峭的阶跃,由此发生了流动分离,说明气体在压力面叶片前缘产生转捩,然后走向比较平滑,而在80%弦长之后,压力系数出现明显下降。对比Re=7×105与Re=1×106,叶片吸力面、压力面P*降低明显,叶片流动损失增大。
当Re=8.2×105时,吸力面在约为35%~45%弦长处,出现了1 个阶跃型的波动,如图16(a)所示。当Re= 1.0×107时,吸力面在约为30%~40%弦长处,出现了1 个微小的扰动,同时发生了流动分离,如图16(b)所示。对比Re= 8.2×105,当Re= 1×107时叶片吸力面P*的最低点升高,叶片流动损失减小。
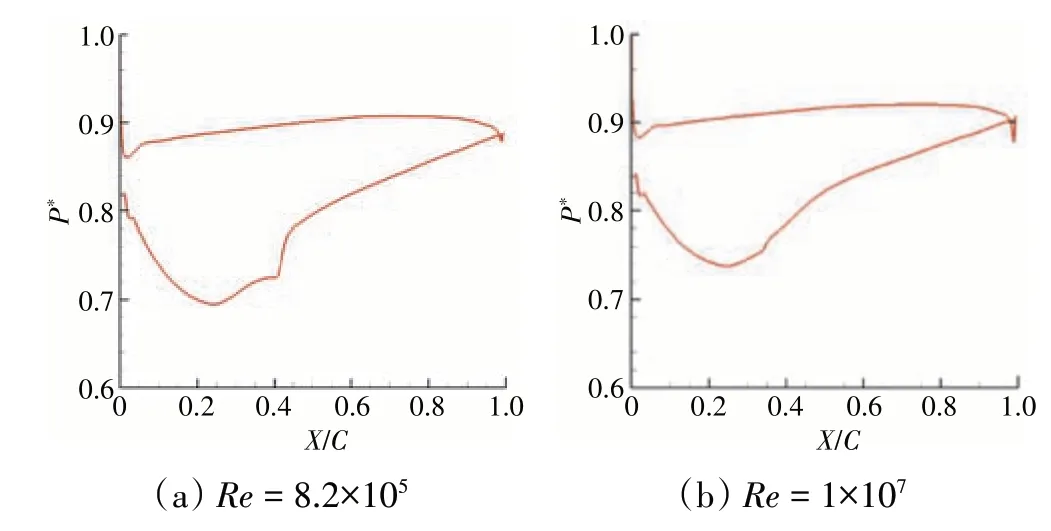
图16 在控制马赫数条件下,当i=0°时的P*分布
2.4 在i = 6°时湍流间歇因子分布对比
选择i= 6°在不控制马赫数条件下,当Re= 7×105、1×106和Ma=0.6时,在Re=8.2×105、1.0×107的工况下进行湍流间歇因子对比分析。
当Re= 7×105时叶型吸力面前缘的湍流因子从0~1 变化时,吸力面发生转捩,边界层变薄如图17(a)所示;而当Re= 1×106时,在叶型吸力面同一位置仍处在稳定的层流边界层状态,在约18.67%弦长处湍流因子从0~1 变化时,发生转捩,随后边界层变薄如图17(b)所示。在Re=1×106、i=6°时叶片的速度分布如图18 所示。从图中可见,在叶片吸力面转捩处,流体速度超过声速,产生激波。在选定叶片与流体工质时,雷诺数的改变只能通过速度与可压缩流体密度的改变。当不控制马赫数时,速度增大是雷诺数增大的最佳途径。在高雷诺数的工况下,流体速度更易达到声速及超声速,生成激波,干扰流体在叶片表面的转捩。

图17 在不控制马赫数条件下,当i = 6°时的湍流间歇因子
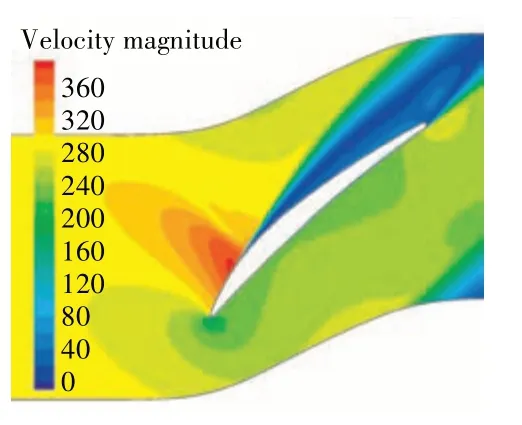
图18 在Re = 1.0×106、i = 6°时的速度分布
在Re=8.2×105时叶型吸力面前缘的湍流因子从0~1 变化,发生转捩,边界层变薄,如图19(a)所示。相比Re=8.2×105,当Re=1×107时叶型吸力面转捩位置前移,且在距离叶片表面更近的位置完成流体从层流到湍流的转变,如图19(b)所示。
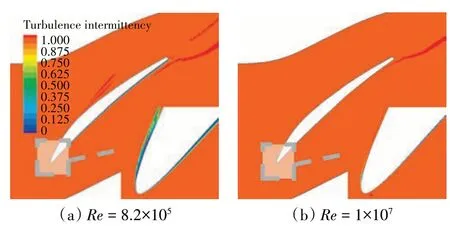
图19 在控制马赫数下,当i = 6°时的湍流间歇因子变化
3 结论
(1)在不控制马赫数的情况下,随着雷诺数的增大总压损失系数不断增大,叶片转捩位置前移。在保持马赫数基本不变、高雷诺数的工况下,随着雷诺数的增大,总压损失系数不断减小,叶片转捩位置前移,但转捩起始位置前移的速度减缓。
(2)当不控制马赫数时,随着雷诺数的增大,流体速度增加。在高雷诺数工况下,流体速度逼近声速乃至超过声速,会在叶片表面产生激波,干扰叶片表面转捩的产生。
