高考数学试题中的线性规划问题——以2023年高考数学全国甲、乙卷有关试题为例

■江西省南昌市新建区第二中学 金 矗

线性规划是基于运筹学背景下的一个实际应用,基本原理是利用线性约束条件求线性目标函数的最值。高中数学关于线性规划的知识出现在不等式章节中,并且每年高考试题中均有对此部分内容的考查。本文以2023年高考数学全国甲、乙卷中线性规划试题为载体,简要分析试题的命制特点及解题思路,以便有效促进和提高同学们对该部分内容的复习效率。

一、线性规划在求最值问题中的应用

例1(2023年全国乙卷理14,文15)若x,y满足约束条件则z=2x-y的最大值为____。

解析：依题意作出可行域,如图1中的阴影部分。由目标函数z=2x-y得y=2xz,其中z取最大值时,其几何意义表示直线系y=2x-z在y轴上截距取最小值。平移直线y=2x,结合目标函数的几何意义可知,当直线过点A时,z取最大值。联立解得即A(5,2),代入目标函数得zmax=2×5-2=8。

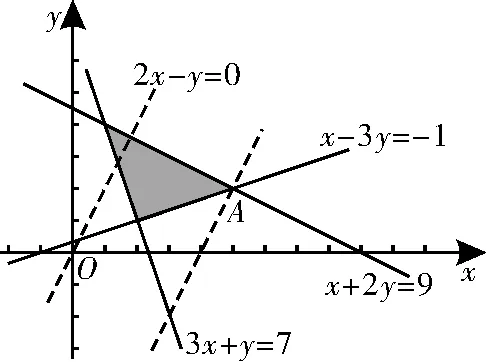
图1

故答案为8。

例2(2023年全国乙卷文11)已知实数x,y满足x2+y2-4x-2y-4=0,则xy的最大值是( )。

解法1：令x-y=k,则x=k+y,代入原式化简得2y2+(2k-6)y+k2-4k-4=0。因为直线x-y=k与圆有公共点,所以Δ≥0,即(2k-6)2-4×2(k2-4k-4)≥0,化简得k2-2k-17≤0,解得,故x-y的最大值是。

解法3：由x2+y2-4x-2y-4=0,可得(x-2)2+(y-1)2=9。设x-y=k,则圆心(2,1)到直线x-y=k的距离d=,解得,所以x-y的最大值为。

故选C。

点评:线性规划不仅仅是一类题型,更是一种数学思想方法的应用。抓住“可行域及目标函数”不放松,从不同角度思考目标函数所具有的几何意义,可以灵活处理相关的一类问题。

二、线性规划在含参问题中的应用

例3(2023 年全国甲卷文/理23 节选)已知f(x)=2|x-a|-a,a＞0。若曲线y=f(x)与x轴所围成的图形的面积为2,求a的值。

解析：依题意可得f(x)=画出f(x)的图像,如图2所示,则f(x)与坐标轴围成△OAD和△ABC,其中,O(0,0),D(0,a),C(a,-a),所以|AB|=a。

点评:此类问题要进行针对性的分析,解题的核心思想是明晰参数所代表的图形表示的几何意义,进而使用线性规划的方法进行求解。这类问题有一定的难度,因为参数不仅可以出现在目标函数中,还可以在约束条件内,故需具体问题具体分析。

三、线性规划在求面积问题中的应用

例4(2023 年全国乙卷文/理23 节选)已知f(x)=2|x|+|x-2|,在直角坐标系xOy中,求不等式组所确定的平面区域的面积。

解析：作出不等式组

表示的平面区域,如图3中的阴影△ABC。

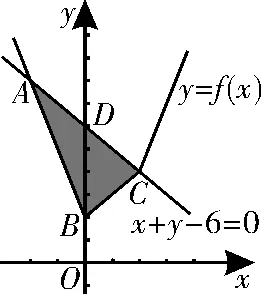
图3

联立解得A(-2,8);

易知B(0,2),D(0,6)。

点评:线性规划在求面积问题中的应用是有通法可循的。绘制可行域、确定平面图形,根据题意进行适当拆分计算出图形面积,进而求出相关量。

线性规划问题在社会发展、生产生活等方面有着重要应用。作为不等式的应用,线性规划问题背后蕴含了数形结合、函数与方程、转化与化归等思想,解决问题的过程中数学抽象、数学建模、数学运算等核心素养有效落实。由于线性规划与函数、不等式等知识有着密切联系,题目综合性强,且在概率、数列等知识模块中有着广泛应用,所以同学们在学习该部分知识时存在一定的困难。因此,同学们在学习线性规划问题时,一定要注重知识的联系与拓展。通过对上述典型例题的分析,引导同学们从多角度、多层次、多维度分析解题思路,从而提升解题技巧。