户内变电站非正交框架梁不规则柱有效长度系数设计方法
2023-11-25荣嵘吕征宇唐晓祥王博炜周锋
荣嵘 吕征宇 唐晓祥 王博炜 周锋
(1.国网上海经研院,上海 200002; 2.同济大学土木工程防灾国家重点实验室,上海 200092)
0 引 言
电力、通信、交通等系统均属于现代城市正常运转的基础设施系统,其中电力系统的正常运行与城市的生存发展息息相关[1]。变电站作为电力系统的转换枢纽,需要具备抵抗危险因素的潜力并维持日常稳定运行[2]。根据其在电力系统中的地位及负荷能力,变电站可以分为枢纽变电站、中间变电站、地区变电站等。其中地区变电站负责直接向地区负荷供电,一旦停电会导致整个地区供电系统的紊乱,又依据电气设备的空间布置,进一步被分为户外变电站、户内变电站和半户外式变电站。本文研究的重点为户内变电站,即主变压器以及高低压电气设备均布置于室内。随着我国城市化的不断推进、用地空间日益紧缺,得益于GIS设备的发展,户内变电站凭借其相对较小的占地空间、便捷的日常管理维护、较强的抵抗恶劣气候能力等优点,成为人口密集地区建设变电站的最佳选择[3]。
以上海地区220 kV户内变电站为例,户内变电站以框架结构为主,通常为2~3层,高度约为10~15 m。由于主变压器及高低压电气设备均布置在户内,减少了总占地面积,但导致结构内部层高要求不同,框架梁缺失,楼板开洞较多,框架梁非正交等特点,对户内变电站框架柱的稳定性能可能产生严重影响[3,5-6],国内外现有规范(GB 50017—2017[7],AISC[8])无法对其稳定性能和有效长度系数进行合理的设计。
框架柱稳定性受到两端边界条件的影响较大,现有框架钢柱有效长度系数设计公式建立在理想假设条件之上,对实际工程中不符合理想假设条件的情况,可通过考虑框架柱非同时屈曲和轴向力实际分布[9]、层间相互作用[10]、支撑刚度[11]、节点半刚性连接[12]、柱间相互作用[13]、层数、刚度比、层间剪力等因素[14]的影响,对现有框架钢柱有效长度系数设计公式进行修正,使其适用于不规则框架结构中。
在户内变电站结构中,部分框架柱存在框架梁非正交的特点,即梁空间夹角导致框架柱两端边界条件不符合规范公式的应用场景。该类型框架柱的屈曲性能和有效长度系数设计方法还有待研究。
本文首先对上海浦东吉春110 kV户内变电站及上海朱松220 kV户内变电站进行调研,从中提取了不规则框架柱的理论模型;接着通过ABAQUS有限元数值模拟研究了非正交框架梁对无侧移框架和有侧移框架中不规则柱屈曲荷载和有效长度系数的影响;最后,在现有规则框架钢柱有效长度系数设计公式的基础上,修正了线刚度比的表达式,使其可适用于户内变电站非正交框架梁不规则柱的稳定设计。
1 非正交框架梁不规则框架结构参数
通过对上海浦东吉春110 kV变电站及上海朱松220 kV变电站的调研,得到非正交框架梁不规则框架结构,如图1所示,其相关参数及取值见表1;该不规则框架结构中的框架柱和框架梁均采用工字钢截面(表2);框架中的结构钢材力学性能参数取值如下:弹性模量E= 2.06×105MPa,泊松比ν= 0.3,屈服应力fy=235 MPa。
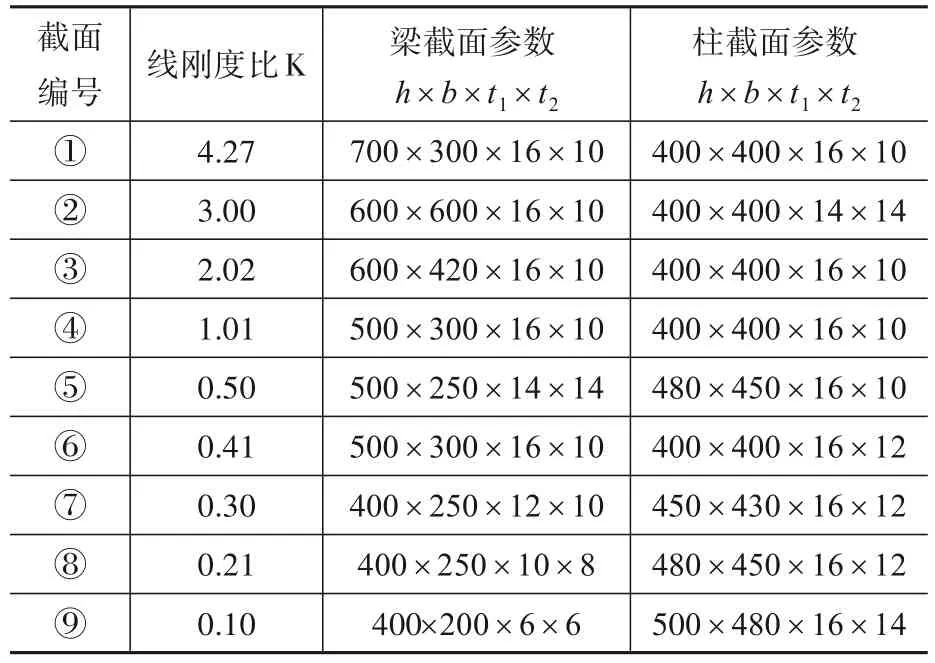
表2 框架梁柱截面几何参数Table 2 Section geometry parameters of frame beam and column

图1 钢框架结构尺寸示意简图(单位:mm)Fig.1 Dimensional diagram of steel frame structure (Unit:mm)
表1中的字母所表达的物理量如图1所示。其中K为梁柱线刚度比值,表达式为
式中:Ib和Ic分别为梁柱截面惯性矩;lb和lc分别为梁柱长度。
非正交框架梁空间夹角如图2所示。框架柱根据所在位置,可以分为边柱、角柱和中柱,其中规则中柱及边柱θ=0°,角柱θ=90°,不规则框架柱θ=0°~90°。
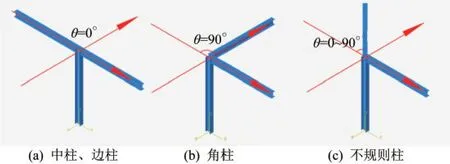
图2 不规则框架非正交框架梁空间夹角示意图Fig.2 Spatial angle of non-orthogonal frame beam in irregular frame
当框架梁空间夹角为0°和90°时,框架柱为符合GB 50017—2017[7]中规定的规则框架柱;而当夹角介于0°~90°之间时,框架柱属于不规则结构,需要考虑框架梁空间夹角的影响。
2 非正交框架梁不规则框架结构数值模拟
本文利用大型通用有限元软件ABAQUS对非正交框架梁不规则柱的屈曲性能和有效长度系数进行研究,分析框架梁空间夹角的影响。
2.1 户内变电站框架模型简化
结合上海地区户内变电站实际结构,对无侧移框架和有侧移框架分别利用大型通用有限元软件ABAQUS建立了完整框架模型。为了便于分析框架梁空间夹角对不规则框架柱屈曲性能和有效长度系数的影响,对无侧移和有侧移两种完整框架模型均进行了简化,如图3所示。简化框架模型保留了完整框架模型中的框架柱,对框架梁取半结构。
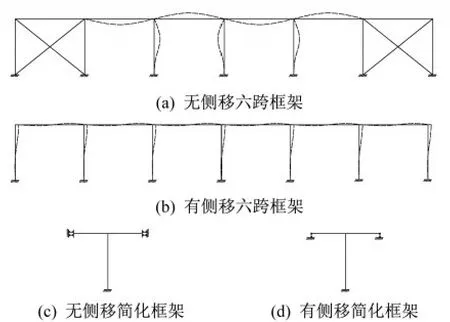
图3 框架挠曲线及简化模型示意图Fig.3 Deflection curve of the frame and simplified model
利用得到的框架柱一阶屈曲模态对应的特征值(即临界屈曲应力),根据欧拉变形公式[式(2)]计算框架柱有效长度系数。通过对比简化框架模型与完整框架模型中框架柱的一阶屈曲模态及其对应的有效长度系数取值,研究了简化模型的适用范围和有效性。
式中:E为弹性模量;I为截面惯性矩;Pcr为临界屈曲荷载;l为构件长度,在本文中等价于框架柱高度H。
采用B21线单元对表2所示六跨户内变电站梁柱平面框架(框架梁空间夹角θ=0°)进行模拟。
为了验证有限元网格尺寸大小对框架柱有效长度系数计算结果的影响,这里选择了无侧移条件下的简化框架模型对有限元模型网格尺寸敏感性进行了分析,网格尺寸大小分别取为10、100和400,计算结果见表3。

表3 有限元模型网格尺寸敏感性分析Table 3 Effect of mesh size on effective length coefficient
由表3可知,有限元模型网格尺寸对框架柱有效长度计算结果影响较小,本文网格最大网格尺寸取为构件长度的1/20。
模型采用线性摄动屈曲分析(buckling),采用子空间算法,特征值个数设置为3,关闭非线性开关,仅考虑弹性状态下的屈曲形式。
边界条件设置和荷载施加如图3所示。根据完整框架结构屈曲后的挠曲线形态,设置简化框架模型中的梁边界。对无侧移框架,简化框架模型约束框架梁远端转角位移与水平位移;对有侧移框架,简化框架模型约束框架梁远端竖向位移。在各中柱柱顶施加大小为-1的y竖向荷载,边柱施加大小为-0.5的y竖向荷载。
2.2 无侧移框架对比
无侧移六跨完整框架模型及简化框架模型一阶屈曲模态如图4所示,结构中部底层框架柱的屈曲模态类似,框架结构其余部件屈曲状态下的挠曲线也基本相符。
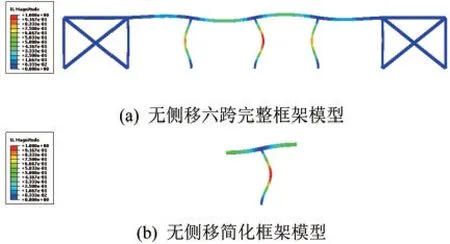
图4 无侧移六跨框架模型与简化框架模型中框架柱一阶屈曲模态位移云图对比(变形放大比例800倍)Fig.4 Comparison of the first buckling mode displacement clouds of frame columns between the six-bay frame and the simplified model (800×, non-sway)
无侧移六跨完整框架模型和简化框架模型中框架柱的一阶屈曲模态对应的有效长度系数计算结果对比见表4,可以看出该简化框架模型可以有效地模拟完整框架模型中框架柱的屈曲性能和有效长度系数。
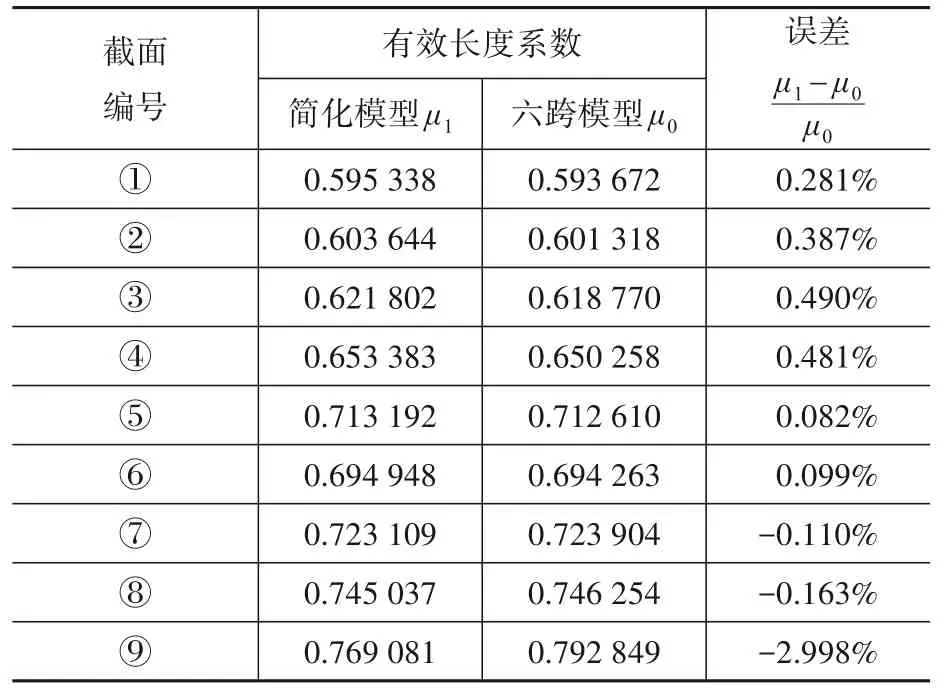
表4 无侧移六跨模型与简化模型有效长度系数对比Table 4 Comparison of effective length coefficient between the six-bay non-sway model and simplified model
表4中的误差来源主要有两个:其一是边柱对于中柱的影响;其二是单元网格尺寸的影响。以下将对边柱的影响进行分析。为验证边柱对中柱的影响,建立了无侧移三跨框架结构和八跨框架结构,并分别在刚度比值K=0.10~4.27的条件下进行了数值模拟计算,数值计算结果对比如图5所示。可以看出,随着框架结构跨数增多,边柱对于中柱的影响减小。简化模型对八跨无侧移框架的模拟优于对于六跨、三跨框架的模拟。
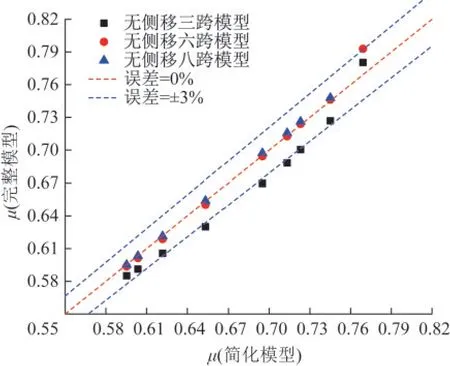
图5 跨数对无侧移框架及简化模型有效长度系数相对误差的影响Fig.5 Effect of span number on the relative error of effective length coefficient of the non-sway frame and simplified model
综上所述,本研究采用的简化模型适用于模拟线刚度比K=0.10~4.27的无侧移框架中柱的屈曲性能和有效长度系数。
2.3 有侧移框架对比
在有侧移条件下,六跨完整框架模型及简化框架模型的一阶屈曲模态如图6所示。从图6中可以看到,完整框架模型与简化框架模型中的中间底层框架柱屈曲模态类似,框架结构其余部件屈曲状态下的挠曲形状和程度也基本相符。
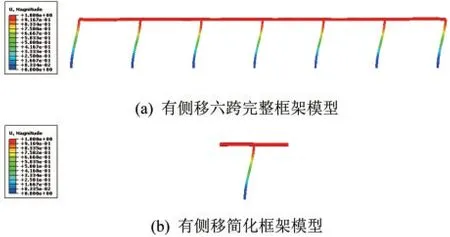
图6 有侧移六跨框架模型与简化框架模型中框架柱一阶屈曲模态位移云图对比(变形放大比例800倍)Fig.6 Comparison of the first buckling mode displacement clouds of frame columns between the six-bay frame and the simplified model (800×, sway)
有侧移六跨完整框架模型和简化框架模型中框架柱的一阶屈曲模态对应的有效长度系数计算结果对比见表5,误差可以接受,该简化模型可以有效地模拟在有侧移条件下完整框架模型中的框架柱屈曲模态和有效长度系数。

表5 有侧移六跨模型与简化模型有效长度系数对比Table 5 Comparison of effective length coefficient between the six-bay sway model and simplified model
为了验证边柱对于中柱有效长度系数的影响,建立了有侧移三跨和八跨的框架结构模型,框架柱有效长度系数误差如图7所示。
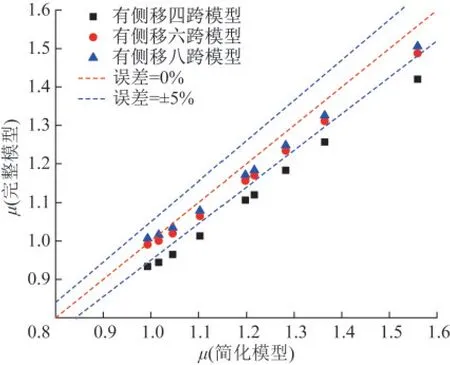
图7 跨数对有侧移框架及简化模型有效长度系数相对误差的影响Fig.7 Effect of span number on the relative error of effective length coefficient of the sway frame and simplified model
有侧移框架柱的屈曲模态受到梁柱截面刚度,边柱等因素的影响,从图7中可以看到,当梁柱截面尺寸较大(线刚度比较大)时,根据简化模型所得有效长度系数更接近根据完整模型所得有效长度系数,随着截面尺寸减小,误差逐渐变大。此外,随着跨数增多,完整模型与简化模型误差减小,即本研究所取的简化模型在误差5%的范围内可以更好地模拟有侧移多跨(大于四跨)完整模型。
综上所述,本研究中所建立的简化模型也适用于模拟线刚度比K=0.10~4.27的有侧移框架中柱的屈曲性能和有效长度系数。
2.4 梁柱框架有限元模型及校核
建立简单的经典梁柱框架模型,通过改变框架梁刚度以及边界条件,分别模拟框架柱一端固接、一端滑移和一端固接、一端自由两种边界情况,利用得到的框架柱一阶屈曲模态对应的特征值(即临界屈曲应力),根据欧拉变形公式[式(2)]计算框架柱有效长度系数。通过对比框架柱数值结果和理论计算值,验证本文提出的简化框架模型有限元建模方法的正确性。
采用与2.1节相同的建模方法,采用B21单元对梁柱平面框架进行模拟,框架柱高度为4 800 mm,框架梁长度为3 000 mm。
模型采用线性摄动屈曲分析(buckling),采用子空间算法,特征值个数设置为3,关闭非线性开关,仅考虑弹性状态下的屈曲形式。
梁柱平面框架边界条件设置和荷载施加如图8所示。框架柱底部固接,限制所有位移与转动。约束框架梁右端竖向位移,通过增大框架梁弹性模量1 000倍取E= 2.06×108MPa,来模拟框架柱底端固接、上端滑移;通过缩小框架梁弹性模量1 000倍取E=2.06×102MPa,来模拟框架柱底端固接、上端自由。框架柱顶端施加大小为-1的集中压荷载。
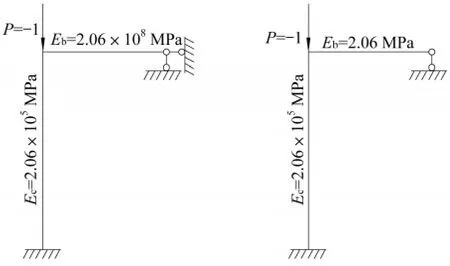
图8 模型边界条件及荷载示意图Fig.8 Boundary Conditions and Loads of model
框架柱在两种边界条件下的一阶屈曲模态如图9所示。
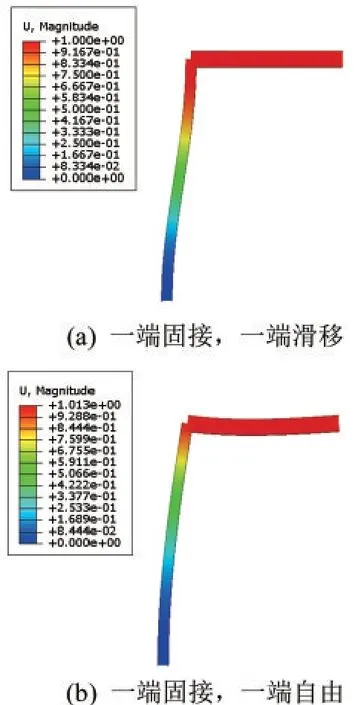
图9 一阶屈曲模态示意图Fig.9 First buckling mode
基于有限元一阶屈曲模态对应的临界屈曲应力,得到框架柱有效长度系数数值结果μ1;根据经典力学理论得到框架柱有效长度系数计算值μ0,则相对误差ferror为
式中:框架柱一端固接、一端滑移边界约束下,μ0=1.0;框架柱一端固接、一端自由边界约束下,μ0=2.0。
利用本文建立的有限元建模方法,对表2各框架柱屈曲性能和有效长度系数进行计算分析。框架柱有效长度系数有限元数值结果与理论计算值相对误差如图10所示,可以看到框架柱有效长度系数数值计算结果与力学理论计算值基本吻合,相对误差较小。据此验证了本文建立的户内变电站简化框架模型可以准确地分析框架柱屈曲性能和有效长度系数。

图10 数值实验和理论计算所得μ相对误差示意图Fig.10 ferror of effective length coefficient obtained from numerical experiments and theoretical calculations
2.5 非正交框架梁不规则柱的屈曲性能
利用经过验证的本文建立的简化框架模型,对户内变电站非正交框架梁不规则底层框架柱和二层框架柱的屈曲性能和有效长度系数进行参数计算,研究框架梁空间夹角θ的影响。参数计算中各模型的参数设置见表1。
对于底层框架柱,柱底固接,限制三个方向的转动自由度和位移。柱顶与框架梁固接。为研究框架柱平面内的屈曲性能,限制框架柱和框架梁面外方向(框架柱为z向,框架梁为局部坐标系下的z向)的位移。为防止框架柱出现扭转失稳,限制绕y轴的转动自由度。在柱顶施加大小为-1的y向荷载。ABAQUS中边界条件设置和荷载施加如图11(a)所示。

图11 不规则框架柱边界条件及荷载示意图Fig.11 Boundary conditions and loads of irregular frame column
对于二层框架柱,柱底和柱顶均与框架梁固接,同时在柱底限制竖向位移,为了保证框架柱在平面内屈曲,限制框架柱和框架梁面外方向的位移(框架柱为z向,框架梁为局部坐标系下的z向)的位移。为防止框架柱出现扭转失稳,限制绕y轴的转动自由度。在柱顶施加大小为-1的竖向(图中为y向)荷载。ABAQUS中边界条件设置和荷载施加如图11(b)所示。
非正交框架梁不规则柱的参数计算结果见表6,随着框架梁空间角度θ的增大,框架柱临界屈曲应力减小,有效长度系数增大。随着线刚度比的减小,框架梁柱节点处的约束减小,有效长度系数增大。
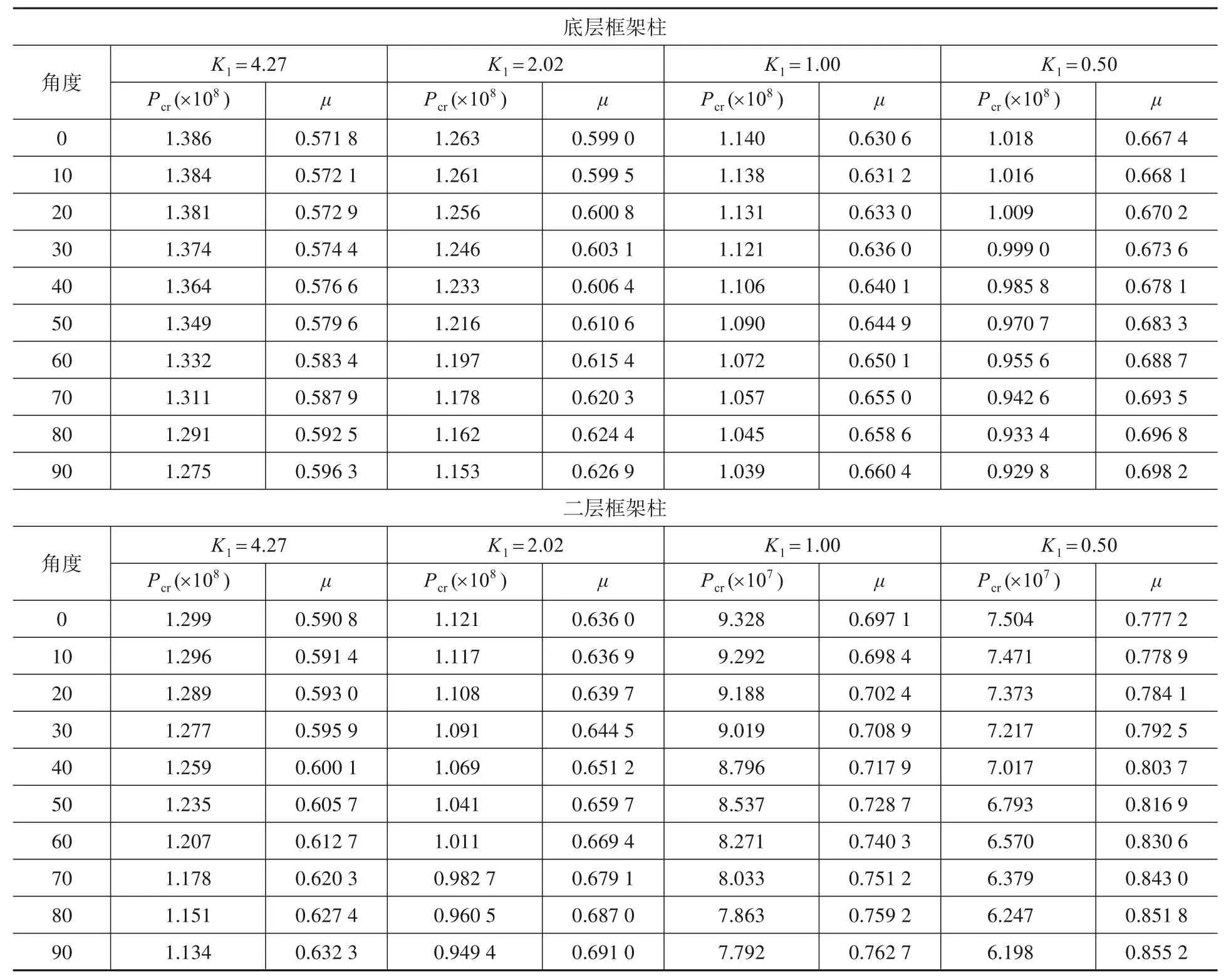
表6 无侧移非正交框架柱有效长度系数Table 6 Effective length factor of non-orthogonal frame columns (no-sway)
3 户内变电站框架柱有效长度系数设计方法研究
3.1 户内变电站规则框架柱
当框架梁空间转角θ为0°和90°时,底层和二层框架柱均属于规则框架柱,以有侧移框架为例,我国规范GB 50017—2017[7]与美国规范AISC 360—05[8]给出了相同的有效长度系数计算表达式。规范设计公式计算其有效长度系数,并与有限元数值计算结果进行比较,其相对误差示于图12。可以看出,对于框架梁空间转角θ为0°和90°的规则框架柱,现有规范设计公式可以较为准确地计算其有效长度系数。
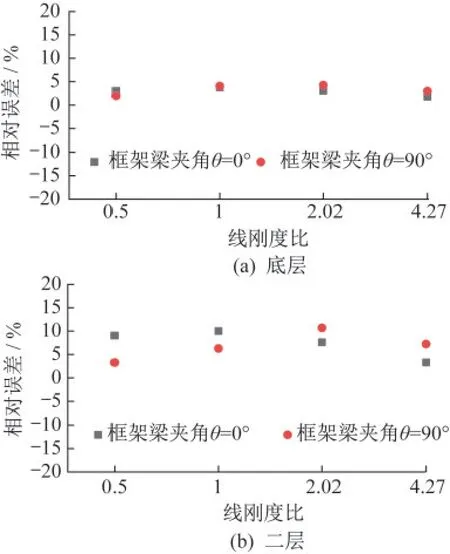
图12 数值结果和规范公式计算值μ相对误差示意图Fig.12 ferror of effective length coefficient obtained from numerical experiments and formula from GB 50017—2017
3.2 户内变电站不规则框架柱
现有规范GB 50017—2017[7]没有给出非正交框架梁不规则柱有效长度系数计算公式,本文基于平衡法对其进行了理论推导,并结合数值计算结果拟合了非正交不规则柱有效长度系数建议计算公式。
3.3 端弯矩与转角位移的关系
图13为两端简支的受弯构件,两端分别作用力矩MA和MB,根据文献[15]建立隔离体的平衡方程(4)。
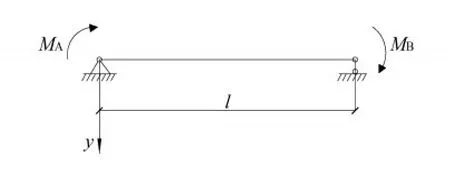
图13 简支压弯构件受力示意图Fig.13 Force diagram of simply supported compression bending member
式(4)的通解为
代入边界条件y(0)=y(l)=0,可得挠曲线方程如下:
构件两端转角分别为
将转角θA和θB当作已知量,杆端弯矩MA和MB当作未知量,则可以得到:
式中,K=EI/l为该构件线刚度;C和S为抗弯刚度系数,其表达式如下:
3.4 框架柱屈曲方程
图14给出无侧移非正交框架梁不规则柱的理论模型,以此推导其屈曲应力方程。

图14 无侧移框架柱屈曲位移示意图Fig.14 Buckling deformation of non-sway frame
为方便模型简化及公式推导,参考GB 50017—2017[7],做如下假定:
(1) 所研究AB柱与其上下相连接的两根柱同时屈曲;
(2) 在同一层中,各横梁两端转角位移相同;
(3) 屈曲时,梁端不平衡力矩根据节点处的线刚度正比例分配;
(4) 所有框架柱均具有相同的抗弯刚度系数;
(5) 不计横梁中轴心力的影响。
根据式(8),可得与节点A相关的梁端、柱端力矩如下:
在xoy平面内,建立节点A的平衡方程,其中θ为AD梁与xoy平面的夹角:
将式(9)代入式(10),可得:
考虑框架梁空间夹角θ的影响,令则式(10)可以写为
同理可得,对节点B有:
根据式(12)和式(13),代入抗弯系数表达式,整理可得框架柱AB的屈曲方程如下:
该方程为超越方程,不便于工程实践应用。参照GB 50017—2017[7],用考虑框架梁空间夹角影响的修正线刚度比K'替换原方程中线刚度比K,即可得到无侧移非正交框架梁不规则柱有效长度系数建议计算公式:
同理,对于有侧移框架柱,也仅需用考虑框架梁空间夹角影响的修正线刚度比K'替换原方程中线刚度比K,即可得到有侧移非正交框架梁不规则柱有效长度系数建议计算公式:
3.5 非正交框架梁不规则柱有效长度系数数值结果与建议公式计算值对比
将非正交框架梁不规则柱有效长度系数建议公式计算值与本文数值结果进行对比,如图15、图16所示。
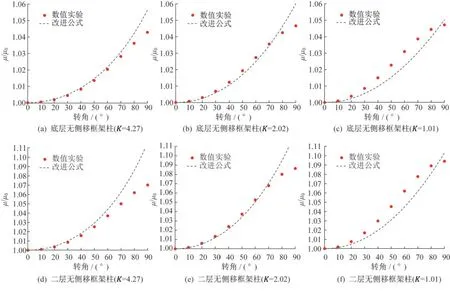
图15 改进公式曲线与数值实验结果对比图(无侧移)Fig.15 Comparison of the improved formula curve and ABAQUS results(non-sway)
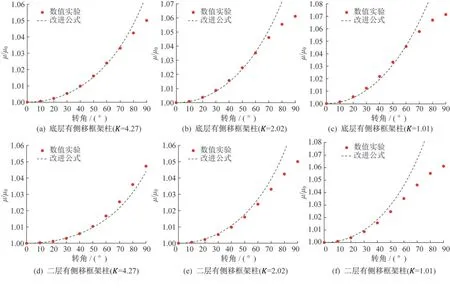
图16 改进公式曲线与数值实验结果对比图(有侧移)Fig.16 Comparison of the improved formula curve and ABAQUS results(sway)
当框架梁空间转角在0°~70°之间,且线刚度比K值较大时,建议计算公式可以较为准确地吻合数值结果;当框架梁空间夹角大于70°时,建议计算公式在计算底层框架柱有效长度系数时,最大相对误差为1.67%,在计算二层框架柱有效长度系数时,最大相对误差为4.25%。
综上所述,本文得到的建议计算公式可以较为准确地计算非正交框架梁不规则柱的有效长度系数。
4 结 论
本文建立并验证了户内变电站框架有限元模型,分析了框架梁空间夹角对不规则柱有效长度系数的影响,并给出了建议计算公式。主要结论如下:
(1) 随着框架梁空间转角增大,不规则框架柱临界屈曲应力减小,有效长度系数增大。
(2) 根据框架柱屈曲方程及规范GB 50017—2017[7]建议的公式,通过修正线刚度比K'=可以反映框架梁空间夹角对不规则柱有效长度系数的影响。
