基于微平面线圈构建的位移量磁调制技术研究
2023-11-25党永迪刘昌荣徐大诚
党永迪,刘昌荣,徐大诚
(苏州大学电子信息学院,江苏苏州 215000)
0 引言
随着微机电系统技术(MEMS)的高速发展,隧道磁阻传感器(TMR)由于具有高灵敏度、小型化、低功耗等特性,应用范围更加广泛[1-2],使得通过力-磁-电多物理场耦合制作高精度加速度计成为可能。TMR传感器虽然具有很高的磁场灵敏度,但是其低频噪声较大。目前抑制磁噪声[3-4]的主要方法有4类,分别是工艺角度抑制、位移磁调制角度抑制[5-8]、斩波技术抑制[9]和磁通量电调制抑制[10-11]。其中,磁通量电调制方法调制效率高,但是用于该调制方式的调制膜材料特殊,目前并没有普及。位移磁调制方式调制效率高且易于实现,已成为目前抑制磁噪声主要方式。同时,采用TMR制作高精度加速度计[12-13]的难点是如何把位移信号的变化高效转换成磁场的变化。所以研究位移磁调制模型具有一定的意义。
然而目前较少有关于TMR处磁感应强度与磁通调制膜位移量、磁通聚集器间距、微平面线圈电流和匝数的理论研究。所以本文以位移磁调制模型为研究对象,采用定量分析的方法,研究了这4个参数与磁感应强度的关系。
1 位移磁调制磁路模型
在加速度信号的测量中,常用的方法是将加速度信号利用惯性原理,通过质量块转换成位移信号,然后按照图1所示的磁路模型[14]转换成磁信号,利用TMR传感器将磁信号转换成电信号进行测量。

(a)磁场磁路模型
图1(a)表示由磁通聚集器与调制膜构成的空间磁路模型,其中P1是由磁通聚集器与磁通调制膜的空气间隙和磁通调制膜构成的磁路,即调制磁路;P2是由磁通聚集器中间的空气间隙构成的磁路,即敏感磁路;P3表示开放空间磁路,即漏磁链路。图1(b)表示等效磁阻模型,其中RP3表示空间中的漏磁磁路磁阻,由于其磁阻远大于其余2路磁路,所以可以将其视为断路,不予考虑。所以磁通聚集器中间的磁通Φ2可以整理为式(1):
(1)
式中:RP1(1)、RP1(2)、RP1(3)、RP2和RP3分别为聚集器气隙和周围开放空间的等效磁阻;Φ2为P2磁路的磁通量;Φ为空间中的磁通量。
根据式(1),代入磁阻的计算式可以整理为式(2):
(2)
式中:wm、tm、μmeff、d分别为磁通调制膜的宽度、厚度、等效磁导率和位移;tfc和g为磁通聚集器的厚度和磁通聚集器之间的间距。
式(2)表明,磁通聚集器中间的磁通与磁通调制膜的长度和磁通聚集器的宽度没有关系。因此接下来的讨论不考虑这2个参数。
为了验证位移磁调制的可行性,分别通过式(2)对位移求一阶导数和二阶导数(式(3)、式(4)),其中wm-g>0,从式(3)、式(4)中可以看出磁通聚集器中间的磁通是随d变换的单调增加的凸函数,所以这也验证了位移磁调制的可行性。
(3)
(4)
2 位移磁调制数学建模
为了量化各个参数与磁感应强度B的关系,使用Maxwell软件进行建模。各个参数的变化范围如表1所示。磁噪声可以采用在平面线圈中通交流电的方式抑制,所以磁场源采用微平面线圈。调制膜和磁通聚集器的厚度分别设置为1 μm,材料选择坡莫合金(相对磁导率6 000),其中TMR位于磁通聚集器中间,其效果图如图2。

表1 参数范围

图2 Maxwell定量分析模型
2.1 微平面线圈电流、匝数与B的关系
由第1部分的分析研究可知,磁通聚集器起到聚集磁力线的作用。添加磁通聚集器之后,空间中大于98%的磁通被聚集到磁通聚集器上。为了验证添加磁通聚集器后,TMR处的磁感应强度依旧与线圈的电流I和匝数N成正比,同时为了研究B与I和N的函数关系,本文通过对图2进行定量分析得到图3。图3中,1 Gs=10-4T。
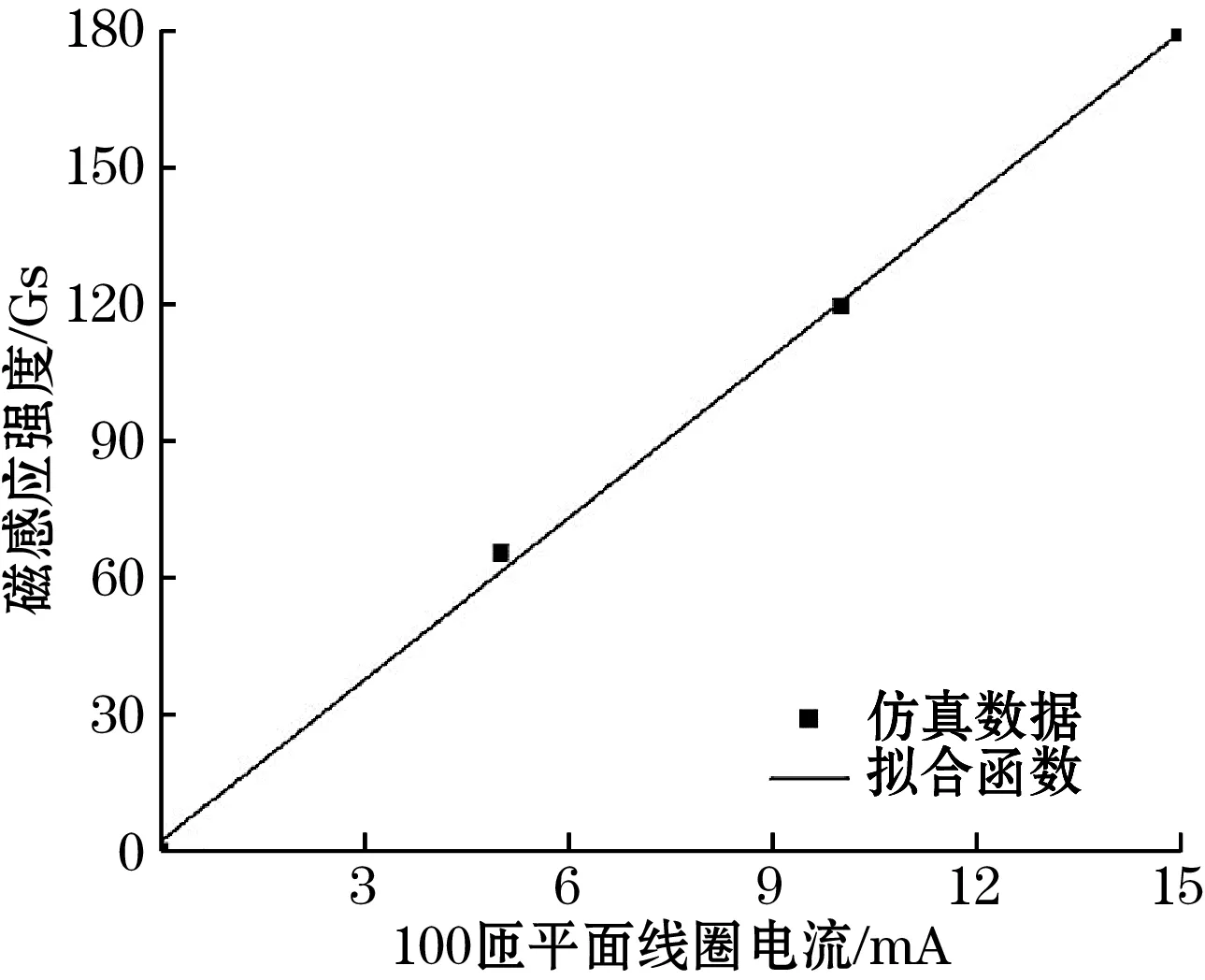
(a)N=100时,TMR处磁感应强度与I的曲线关系
图3(a)是当g=20 μm,N=100,d=10 μm时得到的TMR处的磁感应强度通过拟合得到的曲线。图3(b)曲线是当g=20 μm,I=5 mA,d=10 μm时得到的TMR处的磁感应强度通过拟合得到的曲线,它们的曲线式分别为:
B(I)=PI1I+PI2
(5)
B(N)=PN1N+PN2
(6)
式中:PI1=11.37;PI2=7.45;PN1=0.648;PN2=-0.793。
为了求出B(N,I),假定其满足式(7):
B(N,I)=k1NI+k2I+k3N+b
(7)
联立式(5)~式(7)可以得到式(8)。
B(N,I)=0.115NI-0.159I+0.045N
(8)
2.2 磁通聚集器之间的间距g与B的关系
图4为Maxwell仿真定量分析得到的磁通聚集器之间的间距g与磁感应强度B之间的关系,其中N=10,I=15 mA,d=10 μm。通过拟合得到g与B关系的曲线。其曲线式为式(9),

图4 N=10,I=15 mA,d=10 μm时,g与磁感应强度B的曲线关系
B(g)=aexp(bg)
(9)
式中:a=27.81;b=-0.251 4。
B(g,N,I)=(0.070NI-0.096I+0.045N)exp(-0.025g)
(10)
根据式(8)、式(9),经过简易推理可以得知函数B(g,N,I)满足式(10)。
式(10)可知,磁感应强度与g满足单调下降的e指数形式,对优化g具有指示性作用。
2.3 磁通调制膜位移d与B的关系
图5是在Maxwell软件定量分析下,磁通调制膜位移d与TMR处磁感应强度B之间的关系曲线,其中g=20 μm,N=100,I=5 mA。通过图5可以看出,TMR处的磁感应强度随磁通调制膜位移变化符合第1部分中对于磁路的分析情况,是单调增加的凸函数。通过线性拟合得到B(d)的函数关系为

图5 g=20 μm,N=100,I=5 mA时,磁感应强度与磁通调制膜位移的曲线关系
B(d)=mexp(nd)+pexp(qd)
(11)
式中:m=67.57;n=0.001;p=-64.53;q=-0.35。
根据式(10)、式(11)得出B(N,I,g,d)满足式(12)。
B(N,I,g,d)=(k1NI+k2I+k3N)exp(b1g)+k4(k1NI+
k2I+k3N)exp(b1g)exp(b2d)
式中:k1=1.549;k2=-2.13;k3=1;k4=-0.955;b1=-0.025;b2=-0.346。
2.4 位移磁调制数学模型
综上所述,由式(12)与式(2)可知,当磁通聚集器的厚度和磁通调制膜的厚度以及磁通调制膜的材料已知时,TMR处的磁感应强度符合式(13)的形式。
B(N,I,g,d)=(k1NI+k2I+K3N)exp(b1g)+k4(k1NI+k2I+
k3N)exp(b1g)exp(b2d)
(13)
式中:k1、k2、k3、k4、b1、b2为常数;N为励磁线圈的匝数;I为励磁线圈的电流;g为磁通聚集器之间的宽度;d为磁通调制膜的位移。
为了进一步优化该模型,探究灵敏度与调制效率的关系,联立调制效率式(14)和式(13)可以得到式(15)。
(14)
e=k4[exp(b2dmax)-exp(b2dmin)]×100%
(15)
式中:Bmax为TMR处最大磁感应强度;Bmin为TMR处最小的磁感应强度;Bnf为没有磁通调制膜时TMR处的磁感应强度。
3 数学模型验证
平面单匝线圈对空间中p点产生的磁场效果如图6所示。
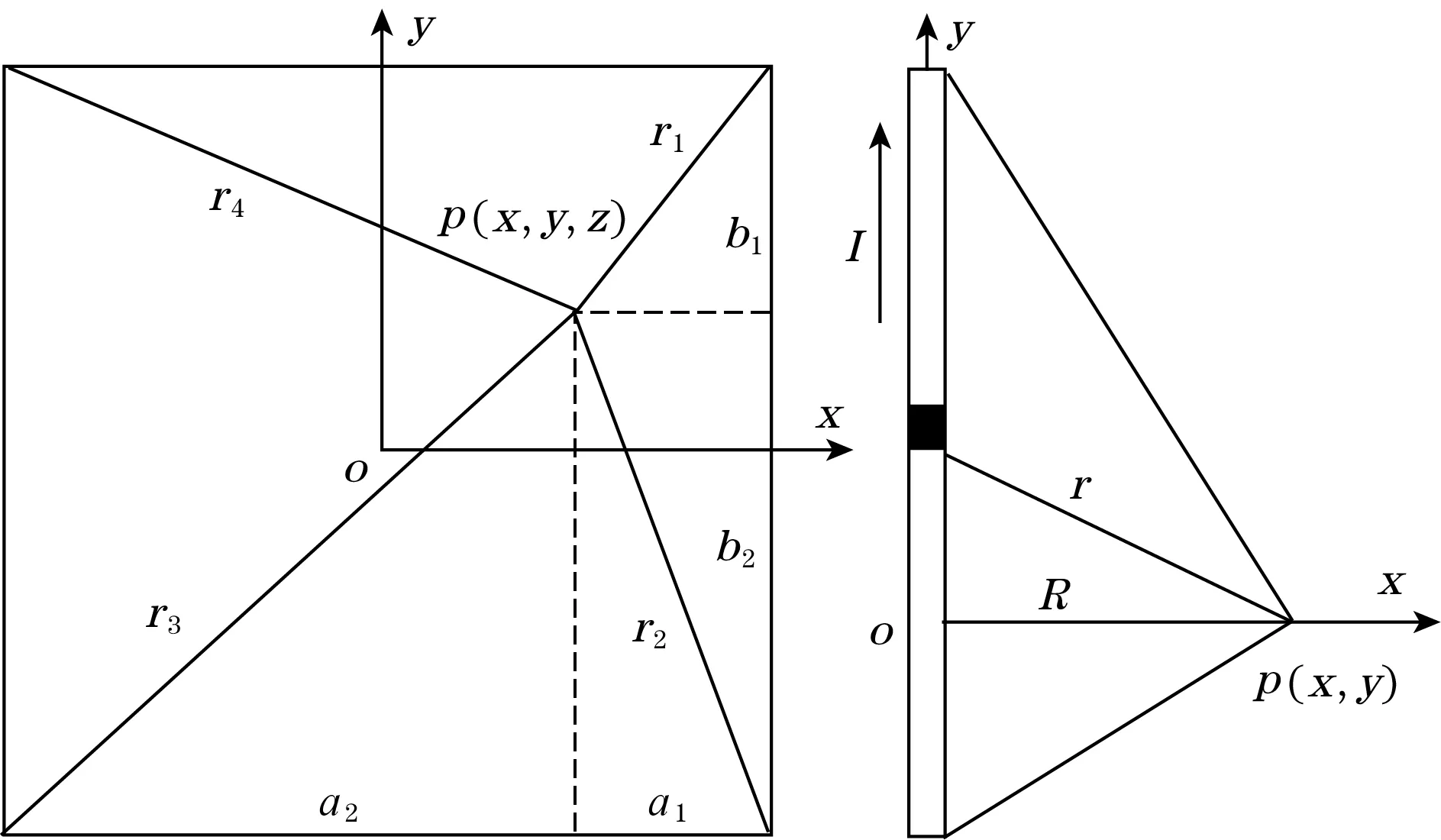
图6 单匝平面线圈的磁场分析
通常认为对于空间中p点的磁场等效于4条直导线对于p点产生的磁场的叠加。根据毕萨定律,可以得到p点x方向的磁感应强度Bx:
(16)
当有N匝线圈时,对所有的平面线圈求和如式(17)。
(17)
当有N匝线圈和M匝线圈时,其比值满足式(18),其中N和M的值越大,这个比值约接近。
(18)
从式(16)和式(18)可以看出TMR处的磁感应强度分别与微平面线圈的匝数和电流成正比。同时,对于式(13),当给定参数g和参数d时,数学模型符合这一规律,所以该数学模型满足毕萨定律,因此验证该数学模型的正确性。
4 数学模型分析
4.1 磁场参数分析
文中通过使用Maxwell软件定量分析的方式,得到TMR处磁感应强度B与N、I、g、d的函数。本部分将对式(12)进行分析,研究磁场对各个参数敏感性。
首先通过式(12)对各个参数分别求导得到式(19)。根据式(19)知,该模型符合对磁路模型的分析,同时函数趋势满足Maxwell定量仿真函数。
(19)
之后,为了研究磁场对每个参数的敏感程度,分别对式(6)、式(10)、式(11)求导,可得式(20)。
(20)
由式(20)可知,磁感应强度B对于微平面线圈电流I最敏感,其次是匝数N和磁通调制膜位移d,最后是磁通聚集器之间的间距g。因此,当优化TMR处的磁感应强度B时,可以优先考虑修改微平面线圈电流I和匝数N。该理论研究为提高基于位移磁调制技术的高精度器件的灵敏度提供了依据。
4.2 调制效率与灵敏度优化
调制效率是区分磁调制技术优劣的重要指标,而灵敏度是高精度器件的必要参数。根据式(3)、式(4)和式(15)可知调制效率与灵敏度反相关,所以研究两者的平衡具有一定意义。
根据数学模型以及MEMS工艺要求,同时为了实现最优解,确定结构参数N为150匝、电流I为12 mA、磁通聚集器间距g为50 μm时,得到调制效率与灵敏度的曲线关系(图7)。由图7可知,当d为5 μm时,可以达到调制效率与灵敏度的最优解。

图7 磁场灵敏度、调制效率与调制膜位移的关系
5 结构参数及应用验证
5.1 结构参数
结合数学模型,确定的系统模型参数如表2所示,其示意图如图8所示。

表2 模型结构参数
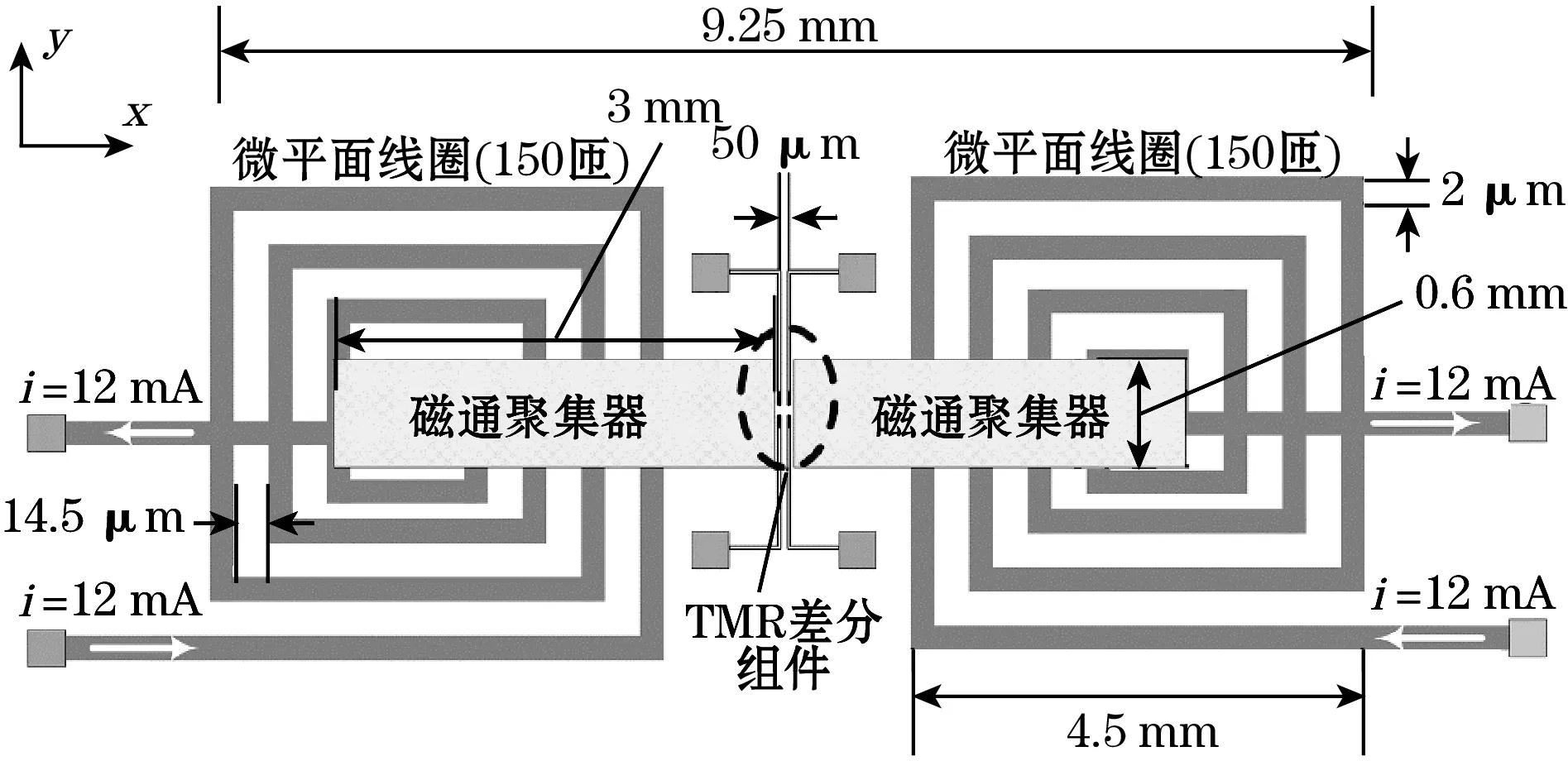
图8 系统参数与模型图
该位移磁调制模型的数学模型为式(21)。根据表2可以得到d与B的关系(式(22)),其灵敏度满足式(23)。
B(N,I,g,d)=(0.106NI+2.16I+0.49N)exp(-0.038g)-
0.917(0.106NI+2.16I+0.49N)
exp(-0.038g)exp(-0.28d)
(21)
B(d)=44-40.34exp(-0.284d)
(22)

(23)
由式(23)可知,当磁通调制膜位移d为3 μm时,系统的最大灵敏度可以达到4.88 Gs/μm(相对磁导率μr=1时,1 T=10 000 Gs=10 000 Oe);d为5 μm时,系统的最大灵敏度可以达到2.72 Gs/μm。由式(15)可知,当3 μm 计算基于位移磁调制技术的隧道磁阻加速度计分辨率的计算式为: Ssystem=Smac·Scoil·STMR (24) (25) 式中:Ssystem为系统灵敏度;Smac为机械灵敏度;Scoil为线圈磁场灵敏度;STMR为TMR灵敏度;Sresolution为系统分辨率;Snoise为TMR磁噪声。 由于实验条件限制,本实验采用PCB制作放大版模型进行验证,参数如表3所示。 表3 模型结构参数 图9(a)表示实验平台,调制膜的位移通过三维滑台左右移动进行控制。为了抑制低频磁噪声,信号发生器频率采用1 kHz。图9(b)为TMR输出电压峰峰值,从结果中可以看出,其趋势符合文中的推导,且结果理想,由于线圈的阻抗与通电电压频率有关,所以当频率为1 kHz时,线圈中的电流只有65 mA左右,这是造成TMR输出电压峰峰值不高的主要原因。 (a)实验平台 基于位移磁调制模型,以高精度TMR加速度计技术为应用对象,研究了位移磁调制模型中TMR处磁场与微平面线圈匝数、电流、磁通聚集器中的间距以及磁通调制膜的位移量之间的关系。数学关系表明,微平面线圈电流是影响TMR处磁场的最敏感因素。同时,进一步研究了灵敏度与调制效率之间的关系,这对于未来进一步推动TMR工程化应用具有意义。5.2 高精度隧道磁阻加速度计技术验证

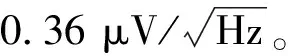
6 实验验证


7 结束语
