磁修正加权EKF多传感器组合导航算法研究

李亚晶,岳 义,韦宝琛,崔国华,刘国兴

(上海工程技术大学机械与汽车工程学院,上海 201620)

0 引言

高精度定位导航技术是移动机器人的关键技术之一[1]。目前,移动机器人的工作环境主要分为结构化环境与非结构化环境,常用的定位导航方式包括惯性导航、全球定位系统、磁钉/磁带导航、二维码导航、超宽带无线通讯技术、毫米雷达、双目视觉、激光雷达等[2]。多传感器组合导航精度相比于单一传感器更高,但仍旧存在着不确定度高的问题[3]。目前冗余多传感器组合导航系统的研究很多,其本质是对多元数据的融合处理。数据融合定义为把来自多个传感器的数据进行关联、估计和组合,以获得目标位置估计[4]。20世纪70年代,国外主要在目标跟踪、导航、信号处理和模式识别等领域进行数据融合的研究;20世纪80年代国内也展开数据融合技术的研究,如1987年成功研制使用多传感器数据融合技术的航空雷达系统,1988年研制成功的气象类雷达系统等[5]。

数据融合主要包括两类方法:概率统计法和人工智能法。其中,人工智能法包括神经网络、模糊逻辑、专家系统、D-S 证据推理等;概率统计法包括贝叶斯估计、互补滤波、统计决策理论、卡尔曼滤波、假设检验等[6]。其中卡尔曼滤波因其简便性与实时性被广泛应用于移动机器人的组合导航中。刘洁瑜等[7]设计了一款卡尔曼滤波器对陀螺仪阵列进行数据融合,对最优估计过程进行了改进,降低了数据处理的复杂度和计算量; GUO等[8]使用联合卡尔曼滤波器融合GPS和INS传感器的多源并行实时数据。然而卡尔曼滤波在针对非线性系统进行滤波融合时会失效,因此利用泰勒展开对非线性方程组直接进行线性化的扩展卡尔曼滤波(extended Kalman filter,EKF)被提出。Sahlholm等[9]基于EKF及平滑算法对车载传感器数据与GPS数据进行融合,利用分布式数据融合来确保在处理其他测量时,道路的存储需求不会增加;Chae等[10]提出了一种结合GPS、编码器和基于EKF的惯性传感器(inertial measurement unit,IMU)的室外定位方法。上述的多传感器数据融合没有考虑到在某类单一传感器故障后系统不确定度增高的问题,使得整个系统的鲁棒性较低。

为了提高系统的可靠性,需要采用同类多传感器对同一目标点进行观测,从而形成冗余数据。Guerrier[11]通过仿真研究传感器数量与精度之间的关系,并且确定了满足系统要求所需的传感器具体数量;程建兴等[12]利用局部状态估计值之间的冗余信息实现其权系数动态的合理分配;Wang等[13]使用16个MEMS IMU 组成一组冗余惯性测量系统,理论上,该IMU阵列的导航精度能够比单个IMU提高4倍,野外实验数据表明导航精度提高了3.4倍,接近理论值;杨军佳等[14]通过分析融合权重对融合精度的影响,确定了最优权值分配原则。上述研究人员选用同类型多传感器测量目标点用以降低信息误差波动,然而该方法不能对自身传感器进行校准。

针对同类型多传感器无法校准自身信息这一问题,WANG等[15]提出了一种基于惯性测量单元阵列-全球定位系统(IMA-GPS)三层数据融合的新型无人机定位系统。使用GPS数据对处理后的多IMU最优测量值进行补偿,使得整体定位精度提高;Bancroft等[16]提出了一种集中式滤波器结构,将多个IMU的导航解与GPS提供的信息进行融合以提高系统的导航精度。Rhudy等[17]研究在非线性递归滤波器预测阶段中,使用的3种不同的冗余多传感器数据融合方法,与使用单个IMU的 GPS/INS传感器融合的结果相比,这3种融合方法均能有效减少横摇和俯仰误差。然而GPS对使用环境等有一定的要求,不能满足室内移动机器人的定位导航要求。

综上所述,针对现有的组合导航系统存在成本高、应用环境受限、定位精度差、不确定度高等问题,本文提出了一种磁修正加权EKF算法用于处理冗余多传感器数据。首先采用最优加权算法处理冗余IMU数据得到最优观测信息;然后通过EKF算法融合系统预测信息与观测信息,得到当前时刻最优状态信息;最后利用冗余磁导航传感器(magnetic guidance sensor,MGS)修正系统累计误差,以确保移动机器人长时间稳定工作。经过MATLAB仿真验证该算法相比于传统EKF算法能更好地改善导航系统的不确定度。

1 冗余组合导航系统

针对现有的定位导航系统存在成本高、安装困难、应用环境受限、定位导航精度低、不确定度高等问题,以 IMU、MGS和RFID(radio frequency identification)读取器为测量元件,搭建了冗余组合导航系统,如图1所示。3个IMU、3个MGS分别安装在移动机器人的上表面与下表面,3个磁钉埋藏在地下与3个MGS一一对应,1个RFID安装在中心偏前,与中心MGS相邻。

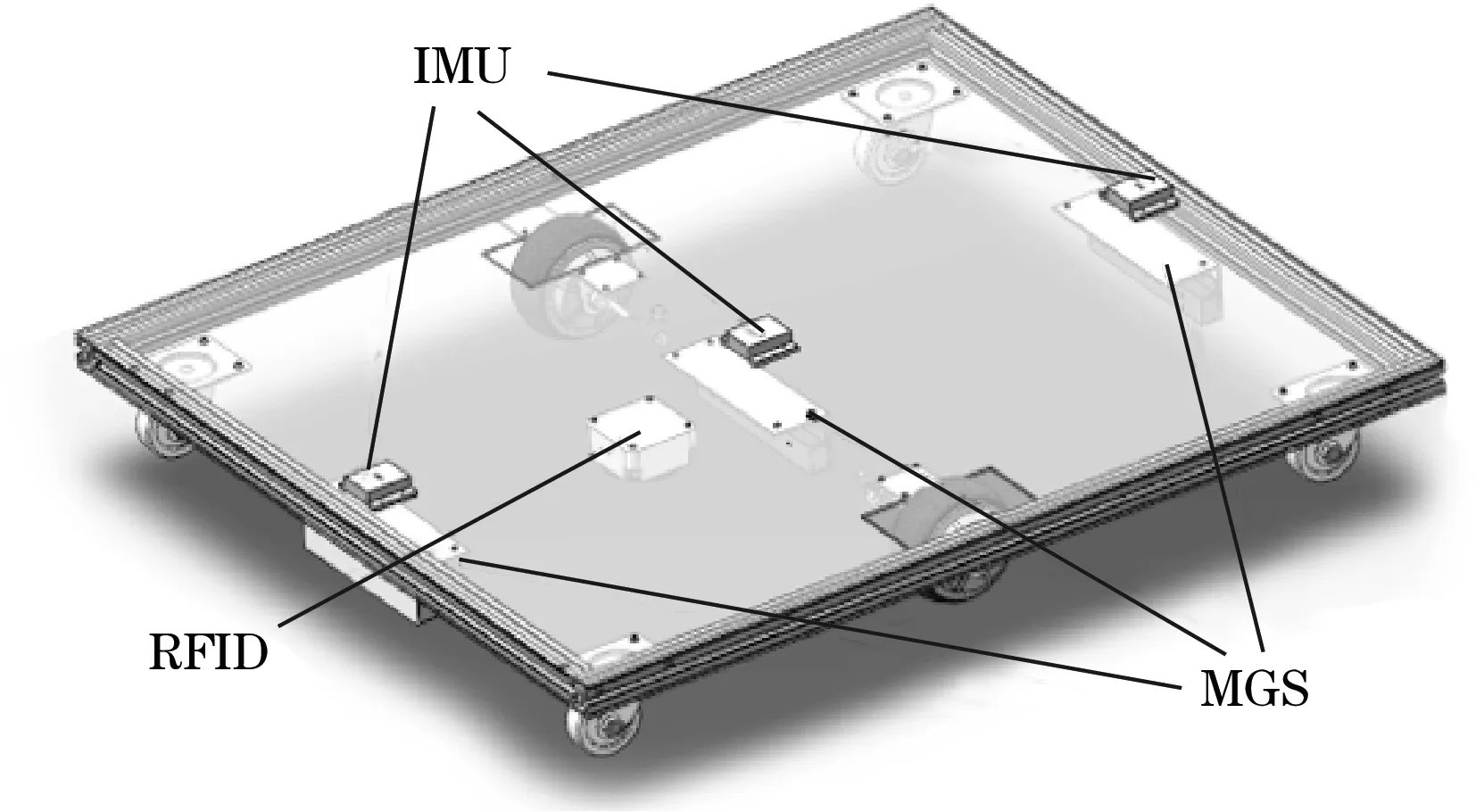
图1 冗余传感器布局

其中,IMU用于测量移动机器人3个方向上的加速度与角速度,用以解算其在世界坐标系中的位移量与偏转角度;MGS用于测量移动机器人中轴线相对于磁钉的横偏距离,解算其中心点位姿的绝对偏差,用以修正IMU的累计误差;RFID用于检测存储在RFID标签中的序号信息,用以提供磁钉的位置编号。冗余组合导航系统的流程图如图2所示。具体实现过程如下:

图2 冗余导航系统

(1)将3个IMU采集到的加速度与角速度信息转换到世界坐标系下,分别解算出各个IMU的位姿信息。

(2)使用3个IMU位姿信息计算载体中心的位姿信息。并通过最优加权融合将冗余信息进行处理,得到最优位姿信息。

(3)将得到的最优位姿信息作为观测值与预测状态进行EKF融合,得到滤波消噪后的系统状态。

(4)对MGS检测到的横偏信息进行KF滤波后再进行位姿解算,依据3个MGS的方差信息进行最优权系数的确定,加权融合冗余定位位姿信息。

(5)将MGS解算出来的定位信息用以修正IMU的累计误差,从而输出更高精度的定位导航信息。

2 磁修正加权EKF算法

现有的定位导航系统主要补偿系统的确定性误差即系统误差,针对随机误差没有很好的解决方法。本文针对组合导航系统的不确定度进行研究,采用磁修正加权EKF算法处理系统的不确定度,相比于传统EKF处理单一传感器数据的结果,不仅降低了系统定位导航误差的不确定度,同时利用间歇性的磁定位信息修正了系统运行过程中长时间的累计误差。

2.1 EKF融合单一IMU

考虑高斯白噪声的非线性状态方程:

xk+1=f(xk,wk)

(1)

(2)

简化为

(3)

式中:Fk为状态转移矩阵;wk为零均值、协方差为Ωk的高斯白噪声。

移动机器人系统状态为[x,y,θ]T,其中x、y为移动机器人在世界坐标系中的位置,θ为移动机器人的航向角。系统的状态方程为

(4)

式中v和ω分别为车体中心处的线速度与角速度。

将(4)式离散化得:

(5)

简化为

Xk+1=FXXk+FUUk+wk

(6)

式中:FX为状态转移矩阵;FU为控制矩阵。

通过FX完成k+1时刻的状态协方差矩阵的更新:

(7)

依据上一时刻的位姿信息以及当前时刻的速度信息对系统的状态进行预测。

考虑具有高斯白噪声的非线性观测方程:

zk=h(xk,vk)

(8)

(9)

简化为

(10)

式中:Hk+1为观测矩阵;vk+1为零均值、协方差为Rk+1的高斯白噪声。

由于IMU输出的位姿是离散形式的,本文的观测信息可描述为

Zk+1=Hk+1Xk+1+Vk+1

(11)

式中Zk+1=[xz,yz,θz]T为IMU观测解算出的移动机器人中心点位姿信息。

k+1时刻的增益矩阵可描述为

(12)

进一步更新k+1时刻的状态协方差矩阵P和最优位姿值为

Pk+1|k+1=(I-Kk+1Hk+1)Pk+1|k

(13)

(14)

2.2 加权EKF融合冗余IMU

针对单一IMU误差不确定度高等问题,通过最优加权EKF处理冗余IMU信息以降低系统的不确定度。加权EKF是在原有的EKF基础上对观测数据进行多IMU观测,依照各个IMU自身的性能,以最小均方根误差为准则选取各个传感器的加权系数。使用多IMU加权融合降低EKF观测数据的不确定度,进而降低整个系统误差的不确定度。

在任意时刻对多IMU进行加权的步骤如下:

(2)建立加权均方误差表达式如下:

(15)

(3)确定最优权系数,令式(15)取最小值,构建如下辅助函数:

(16)

求得最优权系数为

(17)

(4)通过最优权系数对各个传感器的观测数据进行加权融合得到最优观测信息。最优观测信息的均方误差取得最小值为

(18)

(5)将最优观测信息作为EKF的Zk+1观测数据 提供到滤波算法中与状态预测信息相结合推断此刻移动机器人的最优位姿。

2.3 磁定位修正累计误差

冗余IMU仅能降低IMU自身数据的随机波动,对其本身的累计误差没有修正作用。在移动机器人经过磁钉上方时,MGS检测磁钉中心相对于MGS中心即车体中心的相对偏差,通过3组两两MGS的偏差数据与其之间的相对位置结合解算车体航偏角,利用航偏角与横向偏差解算车体中心的位置信息,提供给IMU系统用以清除累计误差。

磁修正加权EKF算法流程如图3所示,其解算步骤如下:

图3 算法流程图

(1)IMU输入三轴加速度与角速度,通过积分解算得到当前时刻位姿信息。

(2)根据3个IMU方差信息确定各自权信息w1、w2和w3,得到最优观测信息。

(3)将最优观测信息与系统预测信息进行EKF融合得到当前时刻最优位姿信息。

(4)车体经过磁钉上方时,3个MGS分别检测其中心与磁钉中心的横向偏差,两两结合确定最优偏差角,进一步解算得到移动机器人中心位姿。

(5)通过MGS系统提供的绝对定位信息修正3个IMU的累计误差。

3 算法仿真验证

本文提出磁修正加权EKF算法的目的在于降低冗余导航系统误差的不确定度。因此,为验证该算法的有效性,对移动机器人的传感器数据进行了仿真实验分析。利用MATLAB软件生成移动机器人的动态轨迹并对传感器真实误差数据进行仿真建模。表1为所用传感器的误差参数,表2为各个传感器的采样频率。

表1 导航误差参数

表2 各传感器采样频率 Hz

设置一条包括前进、原地转向等运动过程的移动机器人行驶路径。移动机器人起始位置(0 m,0 m),规划移动机器人向北行驶8 m,停止后原地旋转90°再向东行驶8 m,原地旋转90°后向南行驶4 m,原地旋转90°后向西行驶4 m,最后原地旋转90°后向北行驶2 m到达指定位置。

针对在同一轨迹上的位置与姿态误差,分别进行了单一IMU的EKF定位导航仿真、3个IMU的加权EKF定位导航仿真以及磁修正冗余IMU定位导航仿真,图4为单一IMU的EKF定位导航轨迹与位姿误差,图5为3个IMU的加权EKF定位导航轨迹与位姿误差,图6为磁修正冗余IMU定位导航轨迹与位姿误差。

(a)行驶路径

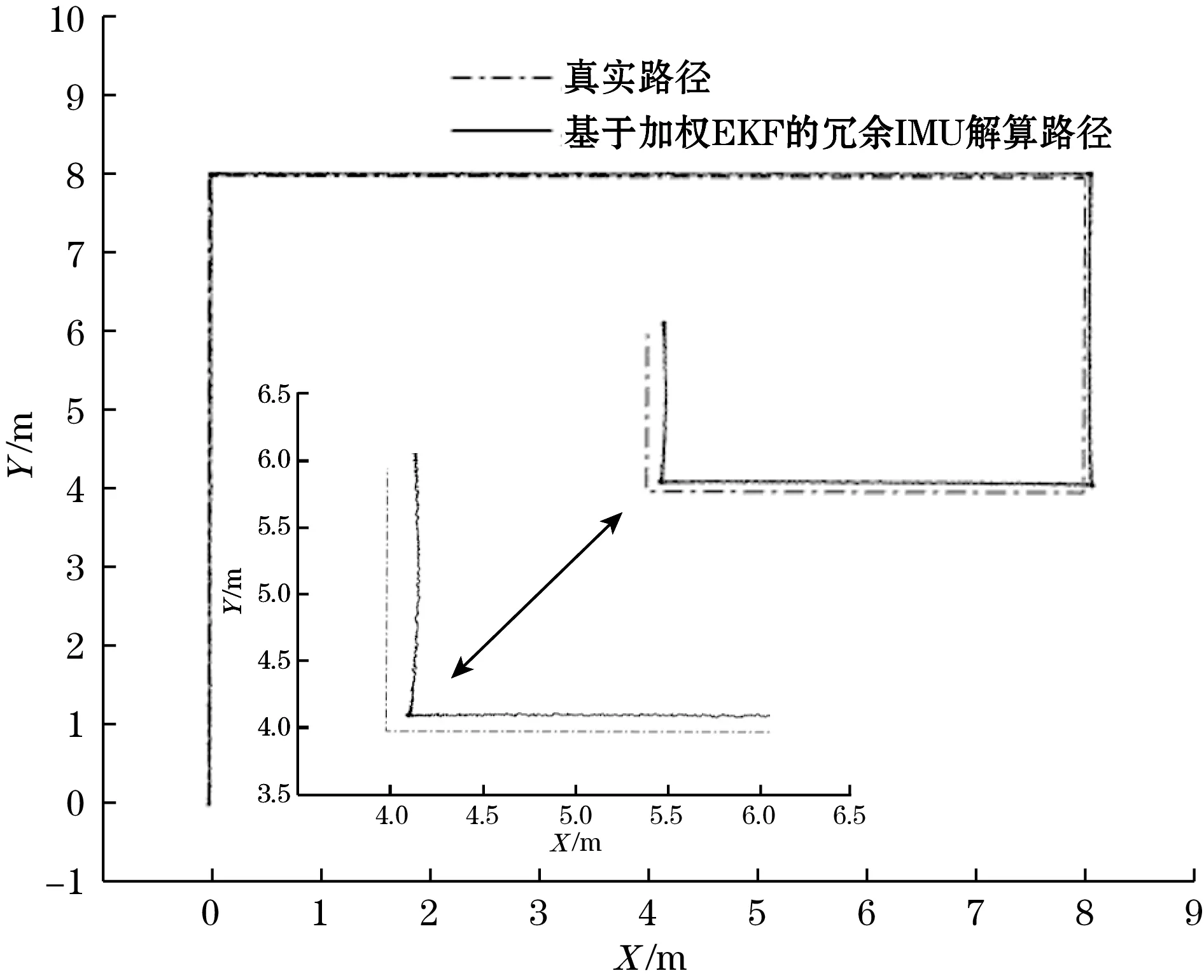
(a)行驶路径

(a)行驶路径

由图4～图6可知,在使用单一IMU作为EKF观测信息与系统状态进行融合时,位置姿态误差随着时间的累积严重漂移,同时IMU的观测噪声不能得到有效抑制,有害观测信息被引入组合导航系统;在使用3个IMU提供冗余观测信息对系统进行修正时,数据不确定度降低了42.3%,但累计误差并没有得到改善,这是IMU传感器本身的特性导致的,增加IMU的数量仅能降低其观测噪声,提高观测信息的可靠性;通过磁修正的冗余IMU导航系统的仿真结果可以在移动机器人经过磁钉上方时,MGS检测到自身相对于磁钉的位姿偏差,提供高精度的位姿参数用以修正IMU的累计误差,从而达到高精度导航的目的。

4 结论

本文为降低移动机器人定位导航误差的不确定度,建立了一套基于多传感器的冗余测量系统,针对该系统提出了一种磁修正加权EKF算法。对冗余IMU信息进行加权融合,相比于单一IMU为系统提供不确定度更低的观测信息用以EKF状态更新;以间歇性的磁信息作为输入去修正冗余IMU系统的累计误差。通过MATLAB软件对系统进行仿真实验,相比于传统的EKF算法,本文的磁修正加权EKF算法不仅能使定位误差的不确定度降低42.3%,同时能针对系统的累计误差进行修正,以达到长时间稳定工作。