基于改进灰色预测的变论域模糊PID温控方法
2023-11-25苏淑靖吴梦香郭杨盛亢叶飞宗意凯
闫 丹,苏淑靖,吴梦香,郭杨盛,亢叶飞,宗意凯
(中北大学,省部共建动态测试技术国家重点实验室,山西太原 030051)
0 引言
离子色谱仪由泵、进样器、色谱分离柱、抑制器和电导检测器等组成,其中色谱分离柱中包含有离子交换树脂。在测定样品时,淋洗液将样品溶液引入色谱分离柱,由于离子对树脂的亲和力具有差异,试样会被分散成不连续的谱带,随后离子被洗脱,由电导检测器检测,进一步确定样品的组成成分。其中色谱分离柱是离子色谱仪核心部分,实验表明即便微小的色谱柱温度变化也会造成不可忽视的基线漂移,进而导致色谱图峰面积波动,最终影响样品浓度测定误差,因此需要对色谱柱温度进行精准控制。
国内针对温度控制的研究主要采用PID控制技术,传统PID控制技术结构简单、鲁棒性强,但是由于柱温箱非线性、时变和时滞大,传统PID调参难度较大且精度不高。文献[1]采用粒子群算法实现PID参数自适应,提高了控制精度,文献[2]基于BP神经网络对PID控制参数进行优化,提升了控制效果,但是上述算法均存在建模难度大的问题,文献[3]结合模糊控制策略和PID控制技术设计了输液温度控制系统,文献[4]提出基于变论域的模糊温度控制方法,有效解决了控制系统非线性、时变带来的问题,然而以上基于模糊PID的控制方法无法自适应调整模糊规则,且仍存在时滞问题。针对以上问题,本文基于PID良好的鲁棒性,结合模糊控制对非线性系统的优化处理,引入一种自适应函数伸缩因子,建立新型变论域模糊PID控制器。同时利用改进离散灰色预测的超前控制特点,有效改善柱温箱温控系统的时滞问题,提高了温度控制精度和动态响应性能。
1 柱温箱温度控制系统
1.1 柱温箱模型建立
色谱柱柱温箱及加热装置如图1、图2所示,色谱柱加载室的上方装有风扇和电阻丝,在加热装置中,通过在电阻丝两端施加电压,驱动电阻丝发热,电阻丝将热量传递给空气,并通过风扇将热量送至色谱柱加载室的色谱柱位置,保证色谱柱处于恒温状态。

图1 柱温箱示意图
在不考虑室内环境对柱温箱影响的情况下,根据热学有关理论知识,利用二阶惯性纯滞后模型构建色谱柱柱温箱的传递函数:
(1)
式中:K为增益常数;τ为滞后时间;T1和T2为控制系统的时间常数。
1.2 色谱柱温度控制原理
本文提出的柱温箱温度控制算法原理如图3所示,在模糊PID控制器的基础上,引入函数伸缩因子实现论域范围的自适应伸缩;同时为解决温度控制的时滞问题[5],在Pt100温度传感器获取柱温箱温度数据后,利用改进灰色预测模型超前预测的特点对控制器进一步优化,减少时滞影响,提高温控精度。

图3 柱温箱温度控制原理图
2 变论域模糊PID控制器设计
2.1 变论域模糊PID温度控制器
传统控制方法常采用PID控制器,在此基础上结合模糊控制原理构成模糊PID控制器。模糊控制器采用传统的双输入三输出结构,将实际温度与设定温度的误差e(t)和误差变化ec(t)作为输入量,经模糊化、模糊推理和模糊决策,输出PID控制器的3个参数修正量ΔKP、ΔKI、ΔKD,可实时修正PID控制参数[6],控制器输出表示为
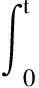
(2)
式中KP、KI和KD为PID控制器的比例调节系数、积分调节系数和微分调节系数。
根据柱温箱温度控制的实际需求结合专家经验,定义e(t)和ec(t)的模糊语言为NB、NM、NS、ZO、PS、PM、PB[7],e(t)的初始论域为[-E1,E1],ec(t)的初始论域为[-E2,E2],输出变量的初始论域为[-U,U],根据e(t)和ec(t)建立三角形隶属度函数。以柱温箱温度值变化规律为依据,结合温控系统的响应速度、超调量等因素,制定模糊控制规则[8],见表1。

表1 ΔKP、ΔKI、ΔKD模糊规则表
引入变论域思想后,变量的论域可表示为
(3)
式中:α、β为伸缩因子。
伸缩因子根据温度误差进行合理调整:温度误差较大时,模糊控制规则无需进行细致划分,论域不伸缩不膨胀;温度误差中等时,粗糙的模糊规则控制效果不佳,论域通过适当收缩将控制规则细化;温度误差向0逼近,论域快速收缩,控制规则划分更为精细,实现了对微小温差更加精确的控制[9]。
2.2 新型伸缩因子设计
伸缩因子是决定变论域控制器性能的关键因素,基于函数模型的论域伸缩因子直接选用某些特殊函数,避免了基于模糊规则的方法因缺乏完善模糊规则导致的控制性能降低的问题。本文基于以下函数模型设计伸缩因子:
(4)
式中ρ1、ρ2、ρ3、ρ4为 伸缩因子参数;θ为因子常量,θ∈[0,1]。
然而,伸缩因子并无具体物理意义,许多学者对这一参数进行了大量研究,到目前为止尚无普遍意义的选值方法,一般根据实际工程需要设定为固定值,这也使得伸缩因子不具备自适应性。针对这一问题,综合考虑多次实验结果对比和伸缩因子选取原则,根据温度误差e(t)和温度误差变化率ec(t)实时调整因子设计参数:
(5)
式中v为充分小的正数,v∈[0,1]。
为保证输入输出变量的协调性,取ρ1=ρ2=ρ3=ρ4,代入式(4)可得新型函数型伸缩因子[10]:
(6)
该新型函数型伸缩因子满足伸缩因子选取的单调性、对偶性、趋零性、协调性以及正规性要求,且稳定有效。此新型伸缩因子构建的NVUFP控制器可应用于恒温箱温控系统,快速调整温度误差和偏差变化率[11]。
3 改进灰色预测模型的变论域模糊温度控制
上述变论域模糊PID控制器可有效改进传统PID控制器在温度控制过程中的非线性、时变问题,但温度控制的时滞问题依然存在,本文将DGM(1,1)(离散灰色预测模型)较好的超前性与变论域模糊PID控制器相结合,改善了温度控制的滞后性,同时提高温度控制精度。
3.1 DGM(1,1)模型
通过分析柱温箱温控系统特点和温度控制策略,结合灰色预测模型超前预测的特点,建立了DGM(1,1)模型,预测过程如下:
步骤1:X(0)为柱温箱历史温度数据,对X(0)温度序列进行叠加,得到新的温度数据序列X(1)[12]。
X(0)=(x(0)(1),x(0)(2),…,x(0)(n))
(7)
(8)
步骤2:构造背景值。对X(1)做相邻均值得到灰色预测模型背景值,得到灰色预测模型的微分方程:
(9)
x(0)(k)+a·z(1)(k)=b,k=2,3,…,n
(10)
式中a、b为待求参数值。
步骤3:建立灰色预测模型。针对上述生成序列构建一阶微分方程,拟合得到白化微分方程:
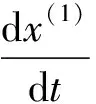
(11)
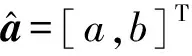
(12)
(13)
式中:B为构造的数据矩阵;Y为构造的数据向量。
计算得方程的解:
(14)
步骤4:相减还原温度数据。对上式进行累减即可得到预测后的温度数据。
(15)
3.2 IDGM(1,1)模型
传统DGM(1,1)模型中背景值系数权值固定不变,忽略了背景值参数对温度预测结果的影响,导致温控系统预测精度较低、误差较大,影响模糊控制器温控效果。对此,本文提出基于矩形法和黄金分割法对传统DGM(1,1)预测模型进行改进,进一步优化背景值参数,提高模型预测精度。图4、图5分别为传统灰色预测背景值参数和改进灰色预测背景值参数图。

图4 传统灰色预测背景值参数
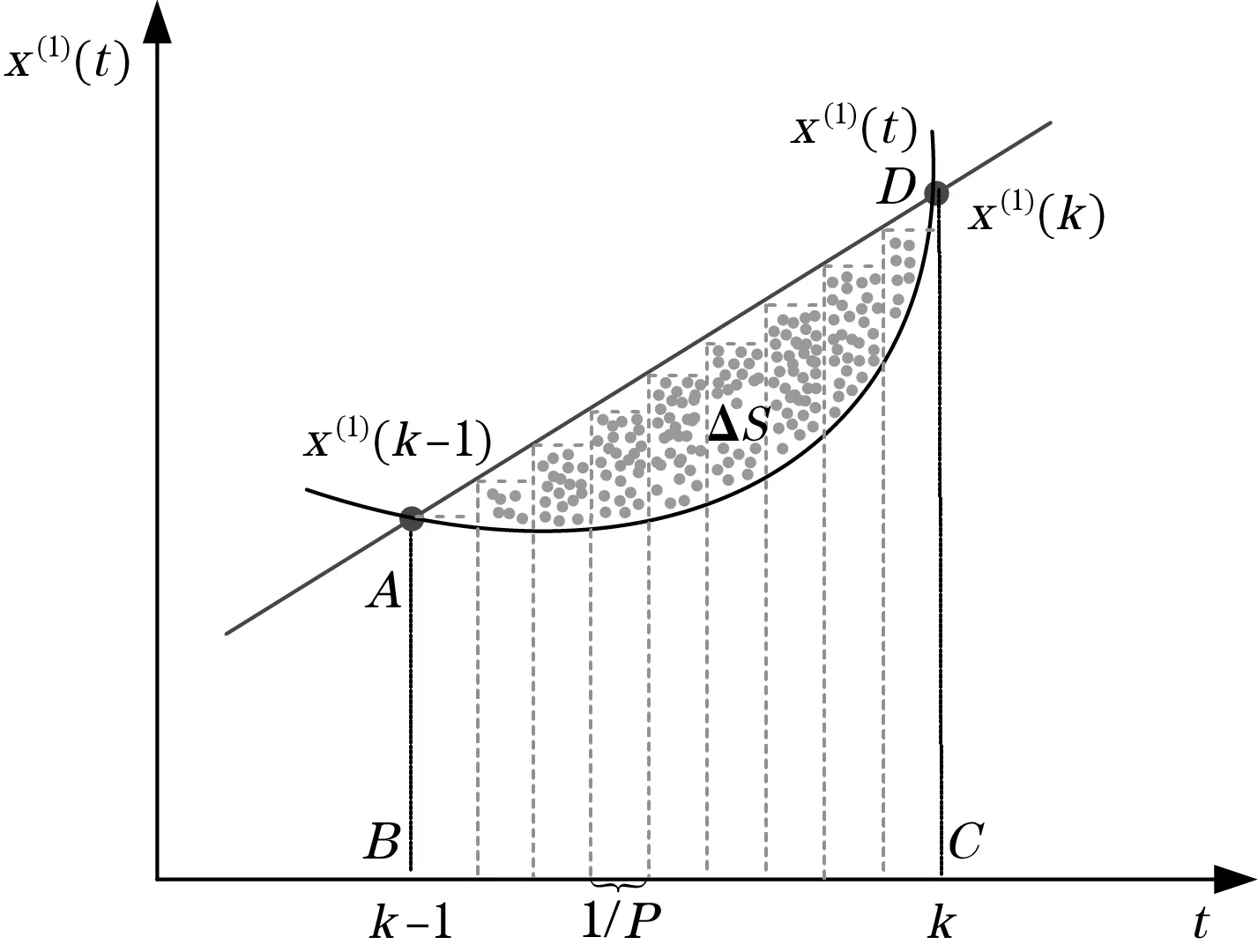
图5 改进灰色预测背景值参数
图4中曲边梯形ABCD的面积可表示为
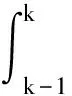
(16)
传统灰色预测模型对上述公式进行简化后,将背景值等效为直角梯形ABCD的面积。
z(1)(k)=(x(1)(k)+x(1)(k-1))/2
(17)
上述2种梯形选取方法存在阴影面积误差ΔS,降低了传统DGM(1,1)温度预测精度,进一步影响温度控制精度。针对上述误差,本文将直角梯形划分为P个小矩形[13],由P个小矩形面积和代替曲边梯形的面积。
z2(k)=1/(2P)[(P+1)x(1)(k-1)+(P-1)x(1)(k)]
(18)
令β=(P+1)/(2P),则1-β=(P-1)/2P,则有
z2(k)=βx(1)(k-1)+(1-β)x(1)(k)
(19)
β也被称为背景值参数,β过小或者过大都会存在面积误差,从理论上讲,应存在一个最佳的β值,使得曲边梯形面积与n个矩形面积之和相等。设改进后的矩形与曲边梯形面积平均误差为E,由上述分析可得,长度为n的温度序列,误差E便可表示为背景值的函数:
(20)
寻找到最优的背景值数值,可减小面积误差,进一步降低模型预测精度。
3.3 背景值寻优
由分析可知,面积误差随背景值参数先减小后增大,构成单谷函数关系[14]。为寻找到最优的背景值参数,采用黄金分割法对单峰函数进行搜索,黄金分割法是在搜索区间[a,b]内,适当插入x1和x22个点,其中x1=a+0.382(b-a),x2=a+0.618(b-a),且处于区间内对称位置,计算其函数值y1=f(x1),y2=f(x2)。若y1
本文建立随背景值参数变化的误差函数E=f(β)。
步骤1:确定搜索区间。背景值参数范围为[a,b],初始值a=0,b=1,精度设定为ε=0.1,记迭代次数k=1。
步骤2:若b-a<ε,则求得最优背景值参数β=(a+b)/2,否则执行步骤3。
步骤3:根据黄金比例分割法插入点β1和β2,β1=a+0.382(b-a),β2=a+0.618(b-a),计算对应的误差E1=f(β1)和E2=f(β2)。
步骤4:若E1 步骤5:令k=k+1,执行步骤2。 图6为误差随迭代次数的变化图,图7为预测前后对比图。由图6及图7看出,采用改进DGM(1,1)模型对长度为40的温度序列进行预测,迭代20次后,面积误差不断减小。与传统灰色预测模型相比,提高了模型预测精度,进一步改善了控制效果。 图6 误差迭代变化图 图7 预测对比图 为了验证柱温箱在离子色谱仪工作过程中的温度控制性能,搭建了柱温箱温控系统并进行仿真实验[15],仿真结果如图8~图11所示。 图8 伸缩因子变化曲线 从仿真结果图8看出,指数型函数伸缩因子参数随温度误差和误差变化率实时调整。其中ρ1变化最大发生在大约150 s处,原因是在此时温度变化最大,根据伸缩因子的模糊调节规则,此时需要较大调整伸缩因子值才能对温度实施更有效的控制。150 s后,温度振荡幅度逐渐减小,伸缩因子数值越来越小,将温度误差调整至更小论域范围内精确控制。伸缩因子的引入使得变论域控制算法不再依赖于专家知识和工程经验,可实现参数的自适应调整,使温控过程变得更加灵活。 从仿真结果图9~图11看出,相比模糊PID和变论域模糊PID,本文的温度控制算法在响应速度、超调量以及稳态精度方面性能更好。 图9 模糊PID温控仿真图 图10 变论域模糊PID温控仿真图 图12、图13分别为柱温箱温度测控平台以及柱温箱温控电路。 图12 色谱柱温度测控平台 图13 温控电路 梯度升温是液相色谱仪最常用的升温方式,将温度升至不同梯度可加强样品溶液各成分的分离度,顺利分离溶液组分。本文首先将柱温箱温度设置为42.00 ℃,在1 100 s和1 400 s分别再将温度设置为38.00 ℃和40.00 ℃,系统间隔2 s采集温度数据,并记录3种温控算法下的温度变化曲线。梯度升温曲线见图14~图16,图16的温度局部放大图如图17~图19所示。 图14 模糊PID温控图 图15 变论域模糊PID温控图 图16 本文算法温控图 图17 第一阶段温度局部放大图 图18 第二阶段温度局部放大图 图19 第三阶段温度局部放大图 从图14~图16温度变化曲线可以看出,柱温箱温度实际控制情况与模型仿真结果基本一致,本文提出的温控算法上升时间更短,超调量更小,且稳态精度更高。将图16中3段温度数据曲线放大后可看出,采用本文温控算法,温控精度可达到±0.03 ℃。 本文提出了一种基于改进灰色预测的自适应模糊PID温控方法,用于色谱柱温度控制中,提出新型函数型伸缩因子实现伸缩因子的自适应调整,同时结合改进灰色预测模型,改善了温控系统的时滞,提高了温控精度。从仿真结果及实验结果看出,与模糊PID、变论域模糊PID相比,本文提出的控制算法温控精度最高,效果最好。
4 仿真结果及分析

4.1 模型仿真

4.2 平台实验


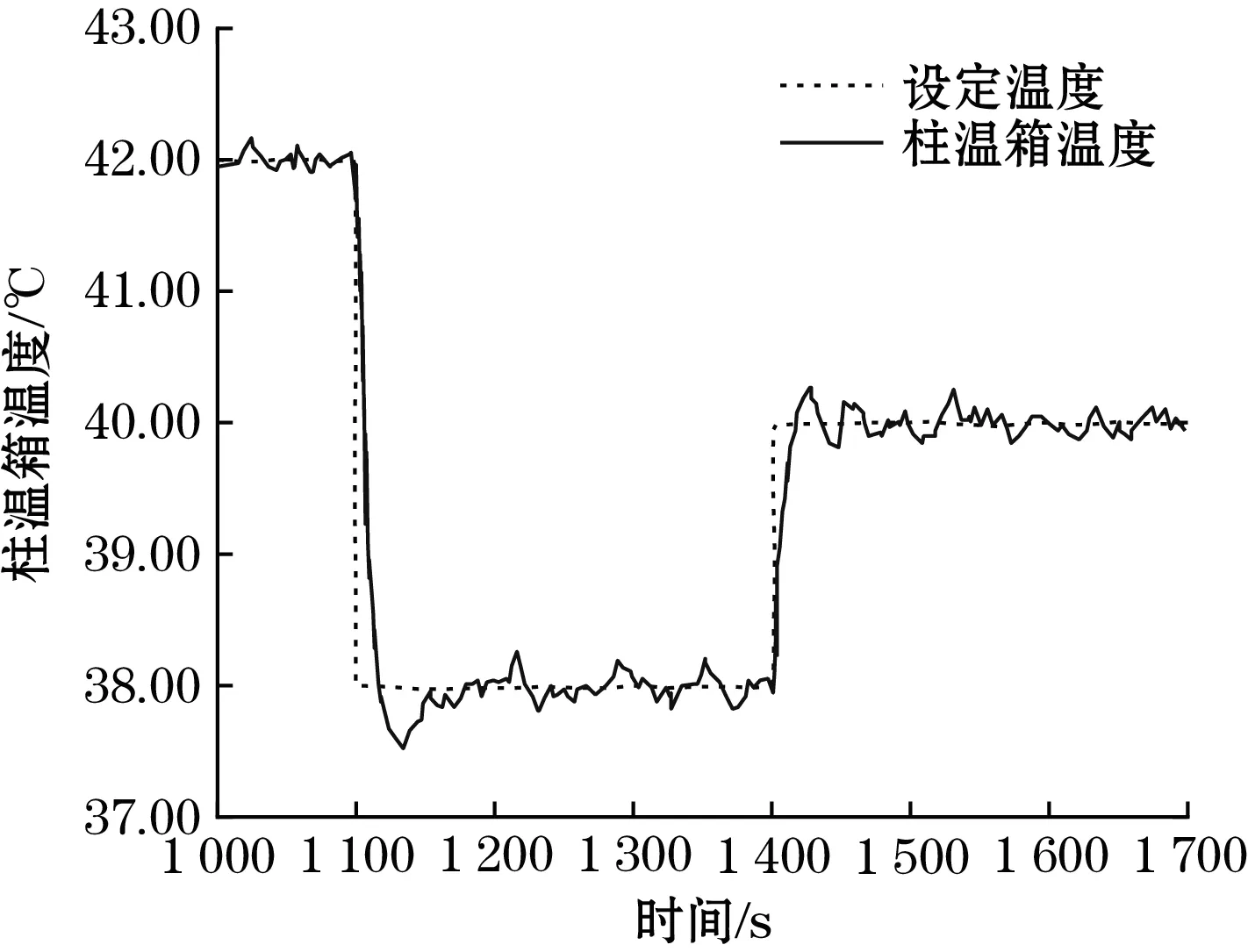

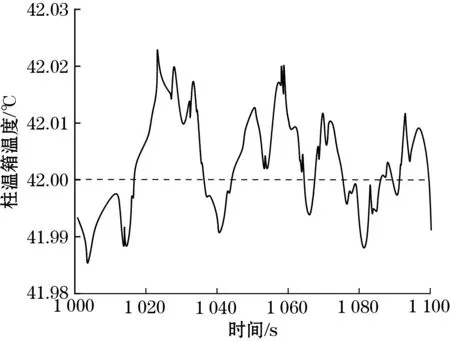


5 结论
