HL-2A 装置高能量离子驱动的比压阿尔芬本征模的扫频行为*

侯玉梅 陈伟 邹云鹏 于利明 石中兵 段旭如

(核工业西南物理研究院,成都 610041)

利用混合磁流体-动理学模拟程序MEGA 对中国环流器二号装置观测到的具有频率啁啾行为的比压阿尔芬本征模进行分析.区别于动理论方法Berk-Breizman 模型,MEGA 程序采用真实的实验参数,如平衡位形、电子密度、电子温度和离子温度等,再现了具有向上和向下扫频特性的比压阿尔芬本征模.实验观测到下扫频行为出现时背景等离子体的参数和比压值相对更高.据此设置MEGA 程序的输入参数: 在下扫频行为模拟中,高能量离子的螺矩角初始分布宽度和芯部比压值,以及扩散系数均更高.模拟结果显示快离子相空间的分布影响了扫频行为.当上扫频行为占主导时,平行于磁场的离子发挥主要作用;而下扫频行为占主导时,垂直于磁场的离子密度显著上升.实验与模拟均表明: 下扫频行为占主导的比压阿尔芬本征模激发对比压值和高能量离子的密度要求更高,这与之前的模拟分析得到的结论一致.

1 引言

可控磁约束聚变装置中,高能量离子主要源于中性束注入(neutral beam injection,NBI)、离子回旋共振加热以及聚变反应.具有较大梯度的高能量离子速度空间分布或压强分布均可提供自由能,并通过波-粒相互作用激发阿尔芬本征模(Alfvén eigenmodes,AEs)[1].高能量离子驱动的阿尔芬本征模可能将高能量离子从等离子体芯部驱至边缘,从而影响电流剖面,降低装置的等离子体约束能力与聚变反应效率,甚至破坏装置的第一壁[2,3].随着波振幅的增长,实验中观测到了非线性特征,并伴随着高能量离子长时间尺度输运过程[4].在未来的燃烧等离子体实验中,阿尔芬本征模与高能量离子之间的相互作用不容忽视,因此,开展高能量离子与阿尔芬不稳定性的线性和非线性相互作用研究,也为将来国际热核实验堆的相关工作提供参考依据.

比压阿尔芬本征模(beta-induced Alfvén eigenmodes,BAEs)是一种典型的离散阿尔芬本征模,比压值β(β=P/(B2/2µ0),其中,P为等离子体压强;B2/2µ0为磁压力,B为磁场,μ0为真空磁导率)对BAEs 的激发至关重要.此外,高能量离子的密度梯度、有限拉莫尔半径和有限轨道宽度效应对BAEs 的激发也有着重要影响[5,6].1993 年,Heidbrink等[7]于DIII-D装置中首次发现了BAEs,并观测到该不稳定性导致了高能量离子的损失.中国环流器二号(HL-2A)装置上高能量电子激发的e-BAEs 于2010 年第一次发现,研究表明e-BAEs的激发与高能量电子的密度、能量和螺矩角密切相关[8,9];此后,在正、反向的低杂波电流驱动的条件下,均观测到高能量电子激发的e-BAEs[10];中性束注入条件下,在HL-2A 装置上观测到了高能量离子激发的BAEs,并利用鱼骨模色散理论(general fishbone-like dispersion relation,GFLDR)进行深入分析[11].2018 年,在EAST 装置上首次观测到了与高Zeff(有效电荷数)杂质注入密切相关的低频率且成对出现的BAEs[12].

可控磁约束聚变装置中,一种常见的高能量粒子驱动的非线性不稳定性—频率啁啾(chirping)行为: 在频谱图中表现为非常快速的扫频现象(一般为ms 量级).具有频率啁啾行为的不稳定性是非线性波-粒相互作用的结果,对研究高能量离子输运过程具有重要意义.在DIII-D[13],JT-60 U[14],MAST[15],NSTX[16],AUG[17],START[18],HL-2A[19]等装置中均观测到了高能量离子驱动的具有频率啁啾行为的剪切阿尔芬波.

关于频率啁啾现象的理论研究,Berk等[20,21]提出了动理论模型—Berk-Breizman 理论,其基于Vlasov-Poisson 模型和Bump-On-Tail 模型,考虑了碰撞项及外部波阻尼,描述一维的等离子体中高能量粒子与静电波的非线性波-粒相互作用.并揭示了频率啁啾行为的成因: 与相空间洞(hole)-块(clump)对(hole-clump pairs) 的运动有关.在非稳态系统中,共振粒子被波的势阱捕获,能量从粒子转移到波,波被激发.不稳定的波振幅会非线性饱和,由共振粒子的驱动项、外部阻尼、粒子弛豫过程和捕获过程间的相互作用共同决定.基于Berk-Breizman 理论,具有频率啁啾行为的阿尔芬不稳定性模拟研究相继展开.Lilley等[22]和Lesur等[23]分别利用BOT 及 δf-COBBLES程序深入研究了速度空间扩散项、动力摩擦项(Fokker-Plank碰撞模型包含了速度空间扩散项与摩擦项)及Krook 碰撞算子(Krook 碰撞模型)对hole-clump pairs 运动的影响,对Berk等[20,21]的工作进行了延伸.Zhang等[24]利用回旋动理学代码GTC 重建了BAEs 在相空间的相干结构,并指出相空间岛的产生(由于非线性粒子捕获)与破坏(由于自由流)存在着竞争关系,并影响着该结构.Zhu等[25]利用动理学代码EAC,讨论了粒子的螺矩角对环效应阿尔芬本征模(toroidal Alfvén eigenmodes,TAEs)非对称扫频现象的影响.非线性混合磁流体(magnetohydrodynamic,MHD)-回旋动理学代码XHMGC 用于研究BAEs 的非线性饱和机制,发现由于径向非均匀性与模结构,饱和振幅的变化尺度被证明与径向共振失谐一致[26].本文利用混合磁流体-动理学模拟程序MEGA[27]探究具有上、下扫频行为的BAEs,区别于之前的模拟,采用了真实的平衡位形与等离子体参数.

对于HL-2A 装置具有频率啁啾行为的阿尔芬本征模,在过去的工作中,本课题组利用 δf-COBBLES 和BOT 程序进行了定性和定量的分析[28,29].在理想的无碰撞、临界条件下,再现了hole-clump pairs 的产生与运动过程,揭示了与频率啁啾行为的关系,并阐明了摩擦系数和扩散系数对具有对称、向上和向下扫频特性的影响.此外,从Bump-On-Tail 分布函数(主要包括共振区被波势场所捕获的粒子)的变化,揭示了hole-clump pairs 的产生原理: 在耗散系统中(阻尼率γd/=0),波-粒非线性相互作用产生的hole-clump pairs 运动导致了分布函数的改变,并释放能量以平衡耗散系统所缺失的部分.当波从高能量粒子中获得能量,高能量区捕获粒子分布函数形成凹陷的hole,频率向上扫;当低能区的捕获粒子获得能量,低能区的粒子分布函数形成堆积的clump,波的表现为向下扫频.但是,在实验中很难获得基于Berk-Breizman 理论的非线性动理学模型中使用的参数,因此,本文采用了磁流体-动理学混合模拟程序MEGA[27].结合HL-2A 装置真实的等离子体参数和平衡位形等,进一步探究具有频率啁啾行为的BAEs.利用MEGA 程序,Wang等[30]对具有频率啁啾行为的TAEs 与高能量粒子模(energetic pareticle mode,EPM)进行了深入研究,发现阿尔芬连续谱影响了扫频的对称性.Bierwage等[31]利用扩展版的MEGA 程序再现了JT-60U 装置的频率啁啾行为,发现增大比热容比值有利于向下扫频行为的激发.需要注意的是,对于常规版的MEGA,动理学方程只应用于高能量的粒子,背景等离子体用磁流体力学方程来描述;对于扩展版的MEGA,高能量的粒子与背景等离子体行为均用动理学方程描述.

本文的结构如下: 第2 节介绍典型的HL-2A装置具有频率啁啾行为的BAEs,并简要分析其模结构与频率;第3 节主要介绍MEGA 程序的物理模型;第4 节介绍利用MEGA 程序,结合实验参数得到的模拟结果,并与实验结果进行对比分析;第5 节则对全文进行总结.

2 HL-2A 装置具有频率啁啾行为的BAEs

HL-2A 装置是我国第一个具有偏滤器位形的托卡马克实验装置,其大半径和小半径分别为R=165 cm,a=40 cm.有两套同向的正离子源(氘)中性束注入加热系统,束与磁轴呈31.9°角切向注入等离子体,目前,单套源的功率和束能量最高可达1 MW、45 keV.HL-2A 装置具备各种高时空分辨率的诊断系统,可对磁流体不稳定性的观测及模结构的测量等研究提供技术支持,如利用Mirnov磁探针、软X 射线阵和微波干涉等诊断手段从磁扰动、密度扰动以及电子温度扰动等多方面来探究磁流体不稳定性.此外,HL-2A 装置发展了电子回旋辐射诊断[32]、汤姆逊激光散射[33]、甲酸激光干涉仪[34]、调频连续波反射计[35]以及电荷交换复合光谱[36]等测量电子温度、电子密度和离子温度等参数的诊断.

典型的具有向上和向下快速扫频行为的BAEs频谱见图1.其中,HL-2A 装置实验第35491 次放电的等离子体基本参数如下: 环向磁场Bt=1.38 T;中性束功率PNBI≈0.45 MW,束能量ENBI≈40 keV,中性束注入时刻t=900 ms.图1(a),(b)分别为电流和NBI 功率随时间的演化,随着时间的推移电流呈现出逐渐上升的趋势;图1 (c)为Mirnov 探针的原始信号,主要测量高能量离子激发的磁流体不稳定性引起的磁扰动;图1(d)为利用Mirnov探针信号进行傅里叶变换得到的频谱图.

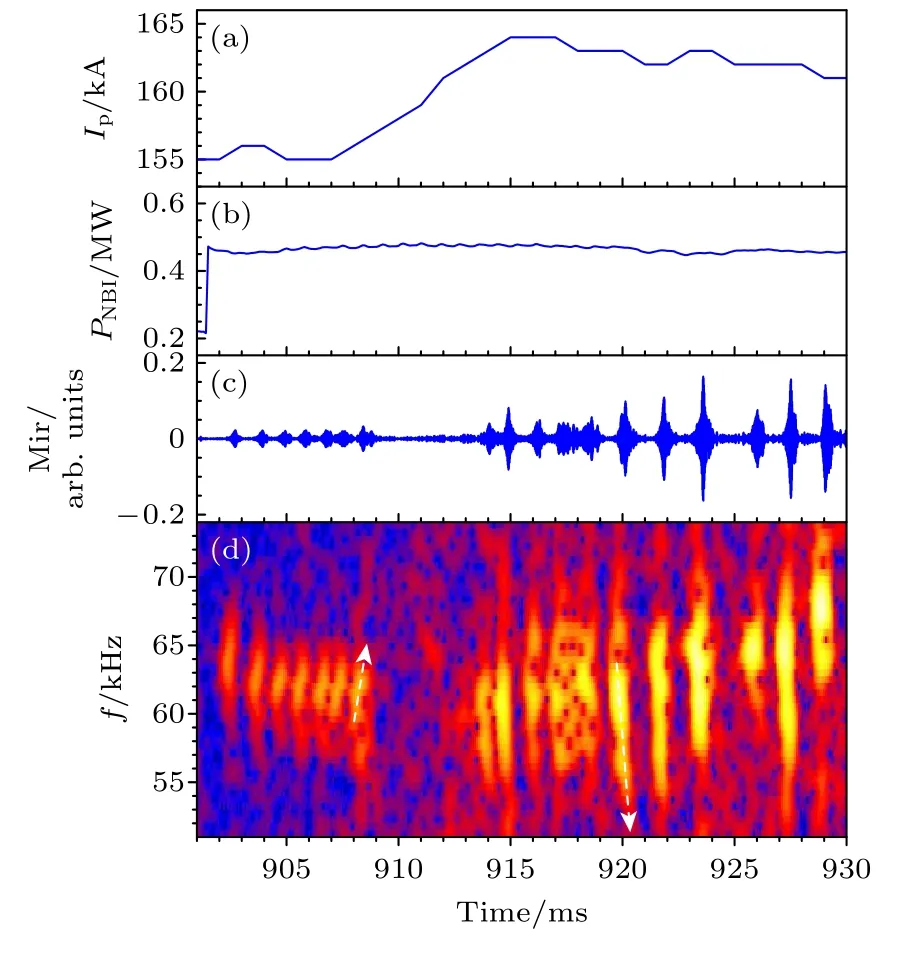
图1 (a)电流和(b)中性束功率随时间的演化;(c) Mirnov探针的原始信号;(d)利用Mirnov 探针信号进行傅里叶变换获得的BAEs 的频谱图Fig.1.Evolution of (a) electric current and (b) the power of NBI;(c) the original signal of Mirnov probes;(d) the frequency spectrogram of BEAs obtained by using Fourier transform with Mirnov probes' signal.

以上扫频特性为主的BAEs 在中性束注入等离子体极短的时间内(≈2 ms)激发,持续时间较短t=902—909 ms.此时,BAEs 的本征频率约为60 kHz,向上扫频的尺度较小 δf ≈5 kHz,扫频的周期较短 δt～ 1 ms.在上扫频特性占主导的BAEs 存在期间,电流的变化尺度较小.芯部电子密度和离子温度随着中性束注入逐渐攀升,出现了以强下扫频特征占主导的BAEs.其本征频率约为65 kHz,扫频的尺度更大 δf～ 10 kHz,扫频的周期更长 δt～ 1.5 ms,持 续时间也更长t=913—930 ms.相较于上扫频行为,下扫频的BAEs 本征频率更高,且Mirnov 探针的信号更强.在HL-2A装置实验中观测到了丰富的以下扫频特性占主导的非线性不稳定性,如鱼骨模[37]、EPM[38]、TAEs[39]和BAEs[28]等.具有上扫频特性的阿尔芬本征模出现的频率较低,常于中性束注入前期被激发,电流和等离子体参数处于爬升阶段.此外,对中性束的功率要求不高(约0.45 MW),但需保持相对较高的等离子体密度.

利用软X 射线阵列得到的频谱见图2.软X 射线主要用于测量等离子体的轫致辐射(Pb∝,其中,Pb为轫致辐射功率,Zeff为有效电荷数,ne为电子密度,Te为电子温度).高能量离子激发的不稳定性会引起等离子体的热起伏,从而导致等离子体热辐射的变化,故软X 射线阵列也常用于高能量离子激发的不稳定性研究.由于软X 射线探测阵列一般由多个阵列组成,使用适当的层析照相技术还可以反演得到磁岛的局域位置、极向模数以及传播方向等重要特征.HL-2A 装置第35491 次放电实验中,仅靠近芯部的软X 射线通道(ρ～0—0.4)观测到了以上扫频行为占主导的BAEs.软X 射线各通道对应的位置见图2(a)SX51,r=2.5cm,ρ～0.065;图2(b) SX49,r=-7.3 cm,ρ～-0.1825;图2(c)SX53,r=12cm,ρ～ 0.3;图2(d) SX54,r=16.3 cm,ρ～ 0.4075.其中,r表示位置半径,ρ表示归一化半径.由于SX52 通道信号缺失,选用了对称位置的位于高场侧的通道SX49.由图2(b)可知,具有频率啁啾行为的BEAs 主要处于等离子体芯部区,且具有相对较宽的模结构.

图2 利用软X 射线阵列信号得到的频谱图(a) SX51,r=2.5cm,ρ～0.065 ;(b) SX49,r=-7.3cm,ρ～-0.1825;(c)SX53,r=12 cm,ρ ～ 0.3;(d) SX54,r=16.3 cm,ρ ～0.4075Fig.2.Frequency spectrogram obtained with soft X-ray arrays'signal:(a)SX51,r=2.5 cm,ρ ～0.065;(b)SX49,r=-7.3cm,ρ ～ -0.1825;(c)SX53,r=12 cm,ρ ～0.3;(d) SX54,r=16.3 cm,ρ ～ 0.4075.

磁探针信号的实验波形见图3,从上到下分别表示的是各个相邻的磁探针拾取的信号.环向和极向磁探针在HL-2A 装置上的详细安装位置见参考文献 [37]的图1.从第一道信号的某相位点(图中选取幅值最高点)垂直画一条直线(相同时刻),判断落到最后一个通道(2π)时相位变化经过了几个周期,以此确定磁扰动的环向模数n和极向模数m以及传播的方向.由图3(a),(b)可确定具有频率啁啾行为的BAEs 的环向和极向模数分别为n=2,m=3,其极化传播方向为离子逆磁漂移方向.

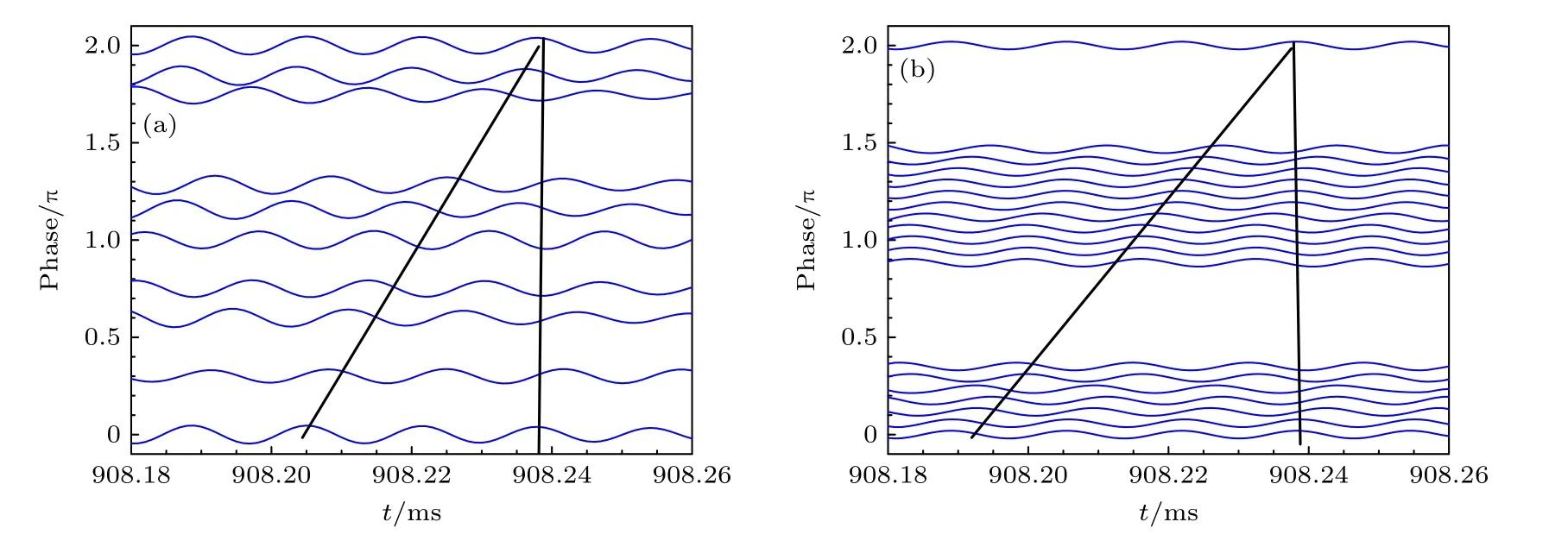
图3 (a)环向和(b)极向磁探针信号.可判断环向模数 n=2,极向模数 m=3Fig.3.(a) Toroidal and (b) porloidal Mirnov probe signal.Toroidal and porloidal mode number are confirmed as n=2 and m=3 by using the phase shift method with toroidal filtered Mirnov signal arrays.

已知BAEs 的频率计算公式:

其中,mi为离子质量,HL-2A 装置中主要为氘离子,mi≈3.34×1027kg.将等离子体参数电子温度Te≈1.1 keV、离子温度Ti≈0.5 keV、离子旋转频率frot≈5 kHz 代入(1)式,t=908 ms 时,BAEs 频率的理论值为fBAE=ωBAE/2π+nfrot≈55 kHz;Te≈1.2 keV,Ti≈0.75 keV,frot≈7 kHz,t=920 ms 时,fBAE≈60 kHz.理论计算得到的值稍低于实验值,误差可能来自于电子温度、离子温度以及离子旋转速度的诊断测量误差.

图4(a)为HL-2A 装置第35491 次放电实验,t=908 ms 对应的等离子体平衡位形,来源于EFIT程序反演计算.最外闭合磁面用红色实线表示,BAEs 的激发位置:q=1.5(安全因子)面用绿色实线标注.图4(b)分别为t=908 ms和t=920 ms两个时刻对应的总的压强(包含了快离子的贡献)和q剖面.已知具有频率啁啾行为的阿尔芬本征模是波-粒相互作用、能量交换的结果,上、下扫频行为分别对应着相空间hole-clump pairs 的反向运动.实验观测到上、下扫频行为出现时刻间隔较短,q分布的变化较小,但是背景等离子体参数和比压值随着中性束注入变化相对较大.压强、扩散系数以及快离子密度上升对于BAEs 的扫频方向有着重要的影响.

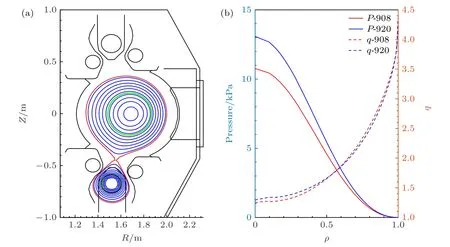
图4 (a) HL-2A 装置第35491 次放电实验,t=908 ms 对应的等离子体位形,最外闭合磁面和q=1.5 面分别用红色、绿色线标注;(b) t=908 ms与t=920 ms 时刻分别对应的总压强和q 剖面分布Fig.4.(a) Magnetic surface shape of HL-2A discharge # 35491 at 908 ms,the last-closed-flux-surface and q=1.5 surface are indicated in red and green,respectively;(b) radial profiles of the total pressure and safety factor at t=908 ms and t=920 ms.

3 物理模型

磁流体-动理学混合模拟程序MEGA 由Todo团队开发,对背景等离子体采用理想的磁流体力学方程组描述,对高能量粒子采用漂移-动理学方程描述[27].高能量粒子的效应通过高能量粒子电流项耦合,高能量粒子的电流密度包括了平行速度、磁曲率、梯度漂移和磁化电流的贡献.MEGA 程序采用的数值方法包括了非线性的粒子模拟(PIC)方法、δf方法、有限差分法(空间和时间上)和显式的龙格库塔法等[27].当高能量粒子的密度远小于背景等离子体时MEGA 物理模型成立.MEGA程序采用了柱坐标(R,φ,Z),其中R,φ,Z分别表示大半径、环向角和垂直坐标.为了模拟中性束注入产生的高能量粒子,本文采用了各向异性慢化分布函数[40]:

4 模拟结果

本文利用MEGA 程序分别对HL-2A 装置具有上、下扫频特性的BAEs 进行模拟分析,选取了对应的t=908 ms与t=920 ms 两个时刻.模拟所必需的平衡位形、压强和q分布等详见图4,其中,模拟区域包含了最外闭合磁面.由于实验已确定BAEs 的模数m=3/n=2,MEGA 模拟中只考虑了高能量离子激发的n=2 的阿尔芬不稳定性.

图5 为HL-2A 装置第35491 次放电实验t=908 ms和t=920 ms 两个时刻分别对应的等离子体参数剖面.图5(a)为电子密度的剖面,芯部(空心圆)和边界(加号)的电子密度分别来源于甲酸激光干涉仪以及调频连续波反射计,两者分别采用不同的符号区分.图5(b)为电子温度剖面,由于芯部电子密度较高,电子回旋辐射诊断信号(空心三角形)在芯部发生了截止.因此,芯部的电子温度来源于汤姆逊激光散射(空心正方形).由于汤姆逊激光散射诊断的时间分辨只有30 ms,故选取邻近时刻点的数据,使得芯部电子温度的数值存在一定的误差.图5(c)离子温度剖面来源于电荷交换复合谱.由图5 可知,随着中性束的注入,离子温度的芯部变化较大;而电子密度和温度在芯部只有小幅度的上升,在边界变化较小.

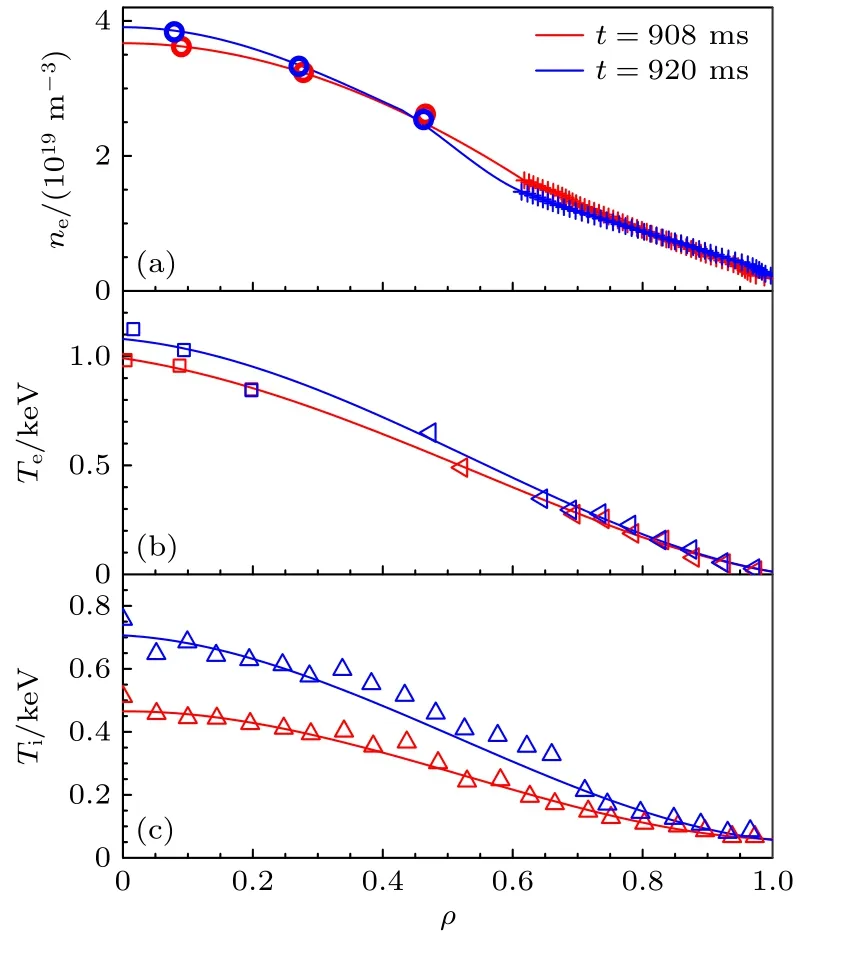
图5 HL-2A 装置第35491 次放电 实验,t=908 ms (红)与t=920 ms (蓝)两个时刻对应的等离子体参数剖面(a)电子密度;(b)电子温度;(c)离子温度Fig.5.Profile of plasma parameters at t=908 ms (red)and t=920 ms (blue) in the shot # 35491 of HL-2A Tokamak: (a) Electron density;(b) electron temperature;(c) ion temperature.

4.1 上扫频行为

HL-2A 装置的中性束主要为切向注入,平行于磁场运动的高能量离子占比相对更高,高能量离子的相空间分布见参考文献 [41]的图4(a).故上扫频行为的模拟中,参数设置如下:Λpeak=0.4,ΔΛ=0.15;初始的高能量离子芯部比压β0=1.2%;黏滞系数和扩散系数相等,ν=νn=10-6vAR0;电阻率η=10-6µ0vAR0,其中vA表示芯部的阿尔芬速度,R0表示装置大半径;中性束的能量E=40 keV.柱坐标(R,φ,Z)对应的网格设置分别为(128,32,128),采用了磁面坐标系下的均匀网格,模拟的粒子数目为219,时间步长 Δt=6.81 ×10-4ms.

利用MEGA 程序与t=908 ms 时刻的等离子体参数,再现了典型的强向上扫频的BAEs.极向速度与相对应的频率随时间的演化见图6.模拟得到的BAEs 本征频率f ≈60 kHz,扫频尺度值δf ≈40 kHz.考虑到模拟中没有加入等离子体旋转的参数,模拟得到的频率误差约有nfrot≈10 kHz.图7为上扫频BAEs 的二维模结构与径向模结构,分别截取了t=0.122 ms (线性)和t=0.166 ms (饱和)两个时刻(图6,黑色虚线标注),均与实验测量值吻合(n=2/m=3),且主要位于ρ～0.4 的位置,这与图4(b)中q=1.5 面对应的径向位置吻合.由图7 可知,该不稳定性具有相对较宽的模结构.线性至饱和阶段没有明显的径向偏移,但是饱和阶段的模结构尺度更宽.

图6 利用MEGA 程序模拟得到的具有上扫频特性的BAEs (a) 极向速度;(b) 频谱图Fig.6.(a) Poloidal velocity and (b) the frequency spectrogram of up-chirping BAEs obtained by MEGA code.

图7 图6 两个时刻(a),(c) t=0.122 ms (线性阶段),(b),(d) t=0.166 ms (非线性阶段)分别对应的二维模结构与径向模结构Fig.7.The 2D mode structure and radial mode structure for different times of (a),(c) t=0.122 ms (the linear growth phase) and(b),(d) t=0.166 ms (the nonlinear phase) corresponding to Fig.6.

基于Berk-Breizman 理论的模拟结果表明,向上扫频的阿尔芬本征模对应着相空间hole 向上运动,而摩擦项增强了该运动,当摩擦项值较大(大于下扫频行为)时使得频率呈现出上扫频占主导的现象[29].可解释HL-2A 装置中上扫频行为发生于密度较高,中性束的能量和功率相对较低,且注入时间较短的条件下.此时的背景等离子体与高能量离子的能量差距较大,碰撞效应影响相对较小.上扫频行为占主导的BAEs 出现既要求高能量离子的密度阈值满足共振激发,又保持相对较低的碰撞效应与比压值,条件相对较苛刻,故该现象在HL-2A 装置出现的频率较低.

4.2 下扫频行为

利用MEGA 程序对HL-2A 装置下扫频BEAs进行模拟时,参数设置如下:Λpeak=0.65,ΔΛ=0.25 ;初始的高能量离子芯部比压β0=1.25%;黏滞系数和扩散系数相等,ν=νn=1.25×10-6vAR0;电阻率η=10-6µ0vAR0.极向速度与相对应的频率随时间的演化见图8.模拟得到的BAEs 本征频率f ≈60 kHz,扫频尺度值 δf ≈30 kHz.考虑到模拟中未导入等离子旋转速度的信息,模拟得到的频率误差约有nfrot≈14 kHz.图9 为下扫频BAEs的二维模结构与径向模结构,分别截取了t=0.147 ms (线性)和t=0.203 ms (饱和)两个时刻(图8,黑色虚线标注).由于选取的两个时刻的q分布变化较小,故与上扫频行为模拟结果近似,模数与实验测量值吻合,主要位于ρ～0.4 的位置,线性至饱和阶段也没有明显的径向偏移,饱和阶段的模结构尺度更宽.

下扫频行为占主导的BAEs 出现时,背景等离子体的参数更高,故MEGA 程序模拟时对黏滞系数、扩散系数和快离子的初始比压值选取相对更大.这表明下扫频行为的出现,需要更高的比压值,该结果与之前的模拟结果一致.Bierwage等[31]通过增加背景等离子体的比热容比影响β值,使得阿尔芬连续谱间隙发生上偏移,增强了EPM 的下扫频行为.该结果可解释HL-2A 装置中,下扫频行为发生时对电子密度、中性束的能量和功率要求相对较低.随着中性束加热背景等离子体,比压值增大,碰撞效应增强,高能量离子的相空间分布发生显著变化,垂直于磁场的高能量离子的密度增加.该条件相对较容易满足,所以HL-2A 装置下扫频行为的不稳定性出现的频率较高.

在下扫频行为占主导的BAEs 模拟中,螺距角的选取与上扫频行为模拟明显不同.两种条件下的高能量离子初始相空间分布见图10 (纵轴v///v表示螺距角,v//表示平行于磁场运动的粒子速度),均是平行于磁场的高能量离子(v//)占主导,这与HL-2A 装置中性束切向入射的情况相吻合.上扫频模拟中,Λpeak＜0.5,几乎是平行于磁场运动的离子占主导;而下扫频行为模拟中,Λpeak＞0.5,垂直于磁场方向的离子密度显著增加,并发挥了重要的作用.在未来的工作中,将进一步深入研究离子轨道对扫频方向的影响.该结果与Zhu等[25]利用EAC 模拟分析上、下扫频行为的TAEs 结果不同,出现该结果的原因可能是MEGA 程序采用了实验中获取的非均匀的背景等离子体分布,且背景压强对于BAEs 的影响较大.

图10 (a)上扫频和(b)下扫频模拟时高能量离子的相空间初始分布Fig.10.Initial distribution of energetic ions in phase space,in the simulation of (a) the up-and (b) down-chirping,respectively.

考虑到计算时间和计算效率,本文中主要用到的粒子数为219,图8(a)分别展示了不同粒子数条件下极向速度随时间的演化: 219(红),222(蓝).两条曲线在线性增长率、频率等几乎一致,因此,在粒子数目为219时系统已经达到很好的收敛度.

5 结论

本文利用混合模拟程序MEGA 对HL-2A 装置具有频率啁啾行为的BAEs 进行了分析.区别于之前的动理论方法,模拟过程中采用了真实的实验参数,如平衡位形、电子密度、电子温度、离子温度等.通过Mirnov 探针信号确定了BAEs 的环向和极向模数n/m=2/3.利用软X 射线阵列进行频谱分析,表明该不稳定性主要位于芯部,且具有相对较宽的模结构.实验观测到具有下扫频特性的BAEs 激发时等离子体的参数和模强度更高.利用MEGA程序再现了具有向上、向下扫频特性的BAEs,模数与实验测量值吻合.与实验结果相比,虽然模拟得到的频率具有一定误差,但是依旧能定性地解释: 上扫频特性为主的BAEs 激发时,平行于磁场的离子占主导.这既要求快离子的密度阈值满足波-粒共振激发BAEs,又需要保持相对较低的碰撞效应与比压值.该条件相对较苛刻,故可解释HL-2A装置中该现象发生的频率较低,发生于等离子体密度较高,中性束的能量和功率相对较低,注入时间较短的条件下.而下扫频特性为主的BAEs 激发时,垂直于磁场运动的离子密度显著增大,且需要更高的比压值与高能量离子密度以增强碰撞效应,使得高能量离子的相空间分布发生变化,这与之前的模拟分析得到的结论一致.该结果可解释HL-2A 装置中,下扫频行为发生时对等离子体密度、中性束的能量和功率要求相对较低,该条件更容易满足,故更容易观测到丰富的具有下扫频行为的不稳定性.

衷心感谢Todo 团队研发的MEGA 程序.感谢论文筹备过程中,日本国立聚变科学研究所的Y.Todo、王灏、王佳磊、李政瀚老师,西南交通大学的王先驱老师,核工业西南物理研究院的王雍钦同学给予的帮助.