复杂裂缝内支撑剂铺置规律及有效支撑面积

崔传智,李景林,吴忠维,姚同玉,曹昕乐

(中国石油大学(华东)石油工程学院,青岛 266580)

携砂液和支撑剂的混合物注入裂缝后,由于重力和地层的滤失作用,支撑剂会在裂缝中发生沉降,注入一定的时间后,支撑剂会规律性地铺置在裂缝中。停止注入后,裂缝内压力减小,在地应力的作用下,裂缝会发生闭合,裂缝稳定后的形态及导流能力与支撑剂的铺置情况有重要联系[1]。

目前中外对裂缝内支撑剂的运移及铺置规律进行了大量的室内实验和数值模拟研究。潘林华等[2]调研大量室内实验、数值模拟和理论分析研究成果,归纳了室内实验与数值模拟方法各自的优缺点。赵振峰等[3]、李恋等[4]、脱直霖[5]和沈云琦等[6]建立不同类型的可视化平板裂缝模型、利用多种评价方式来研究排量、支撑剂粒径、裂缝夹角、砂比等因素对支撑剂铺置的影响,总结支撑剂运移的铺置规律。潘林华等[7]构建了大尺度复杂裂缝支撑剂运移与展布评价实验系统,研究主次裂缝中支撑剂运移及展布。彭欢等[8]通过将无序的复杂裂缝离散化得到正交立体的复杂裂缝物理模型,并形成了整套页岩复杂裂缝中支撑剂铺置特征实验装置。郭建春等[9]建立了支撑剂在三维裂缝的运移分布模型,通过引入支撑剂对流质量传递方程研究流、温分布、压裂液滤失等因素对支撑剂运移的影响。曾军胜等[10]和黄志文等[11]利用两种不同的数值模拟方法,建立流-固耦合作用的携砂液流动模型,研究单缝及多级裂缝中支撑剂的运移规律。葛强等[12]利用数值模拟方法研究了复杂裂缝中CO2流体携砂规律。张涛等[13]和狄伟[14]利用数值模拟方法研究支撑剂在裂缝中的运移规律,并利用物理模拟实验对数值模型进行验证及校正。张矿生等[15]、彭欢等[16]、任岚等[17]和张潦源等[18]探索了低密度支撑剂及不同粒径组合支撑剂在裂缝中运移规律。郝丽华[19]采用数值模拟方法,发现主次裂缝内砂堤均表现为“先高度,后长度”的生长模式。陈志强等[20]提出液量分配模型及支撑剂转向输运条件,发现裂缝夹角对于液量分配的影响本质是对于分支裂缝缝宽的影响,并研究天然裂缝开启程度对于压裂液分配情况及支撑剂输运的影响。以上研究涉及多个方面,如裂缝中支撑剂的生长规律、支撑剂裂缝内的铺置特征及相关参数优化等。

现通过数值模拟方法研究支撑剂在裂缝内的铺置规律,分析砂比、黏度等因素对支撑面积的影响,揭示复杂裂缝内支撑剂铺置特征。研究过程中发现一组数据需要数小时甚至十几个小时才能完成计算,模拟时间较长,不便于进行参数范围确定及参数优化;基于数值模拟方法得到的数据样本,运用BP神经网络建立复杂裂缝内支撑剂支撑面积预测模型,得到裂缝内有效支撑面积简便、快速预测方法,旨在较短时间内得到不同数据对应的支撑面积,为选择合适的注入排量、支撑剂等提供便利,为非常规油气藏的压裂开发提供理论帮助。

1 复杂裂缝支撑剂运移数学模型及求解

复杂裂缝中支撑剂运移及铺置的数值模拟研究主要是基于计算流体力学(computational fluid dynamics,CFD)方法,本文研究运用欧拉-欧拉固液两相流模型,该模型将固相视为拟流体,固液两相在空间任意点均存在各自不同的速度、温度和密度,固相分布在液相中且存在滑移,针对每一相均建立动量方程和连续性方程,通过压力和相间交换系数耦合来计算求解,得到两相各自的体积分数。复杂裂缝支撑剂运移数学模型包括连续性方程与动量守恒方程[21];其中,连续性方程为

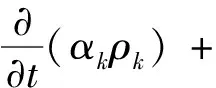
(1)

式(1)中:k为相参数;αk为k相的体积分数,无因次;ρk为k相的密度,kg/m3;νk为k相的速度,m/s;t为时间,s。

动量守恒方程为

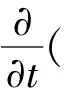
(2)

式(2)中:p为流场压力,Pa;g为重力加速度,m/s2;τk为k相的剪切应力张量,Pa;fp为动量源项,包括固体颗粒间的碰撞力Fs和相间动量传递项MK。

固体颗粒间的碰撞力Fs的表达式为

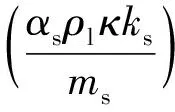
(3)

(4)

液固两相流动过程中,固体颗粒会受到液体的作用力,主要包括浮力、曳力、虚拟质量力等。浮力FL是液相剪切颗粒相产生的径向作用力,曳力FD是液相与固相颗粒间的摩擦力,压力梯度力FVM是固相颗粒由于加速运动对液相产生的阻力。相间动量传递项MK是以上3项构成的,即

MK=FL+FD+FVM

(5)

FL=CLαsρl(vl-vs)∇vl

(6)

(7)

(8)

式中:CL为升力系数,取0.25;vl、vs分别为液相、固相速度,m/s;π为圆周率,取3.14;CVM为压力梯度力系数,取0.5。

本文的计算流体力学仿真模拟中,控制方程组的离散方法采用的是有限体积法,选用基于压力的求解器,压力和速度耦合采用Phase Coupled SIMPLE算法。湍流模型选择标准化的k-ε湍流模型,使用标准壁面函数;曳力计算选用的是由Ergun模型和Wen &Yu模型组合构成的Gidaspow模型。SIMPLE算法的求解思路是基于交错网格求解压力场,再通过压力场求解动量方程,然后得到速度场。具体求解步骤为:①假设一个速度分布,用于计算首次迭代时的动量离散方程中的系数和常数项;②假定一个压力场,给出压力猜测值P1;③根据当前的速度场及压力场,计算动量离散方程等方程中的系数及常数项;④求解动量离散方程;⑤根据速度u、v、w求解压力修正方程;⑥修正压力和速度;⑦求解其他方程,判断是否收敛,若收敛则计算结束,若不收敛则重复步骤③～步骤⑥。

2 模型参数设置

矿场实际裂缝长度一般在百米以上,且高度也能达到几十米,如果在软件中建立实际尺寸的模型,模型计算量会非常大,为避免此情况,本文研究利用流体力学中的相似原理建立等比例缩小的模型,建立的模型需要满足几何相似,运动相似和动力相似。

本文建立的模型是常见的3T缝网模型,模型是由三级裂缝构成,次级缝位于主裂缝的1/2处,三级缝位于次级缝的1/2处。各级裂缝的分支角度均为90°,裂缝高度保持一致,主、次缝长度相等,三级缝长度为次裂缝长度的1/2。裂缝宽度依次减小,主裂缝宽度最大,三级缝宽度最小。

依据几何相似,将实际裂缝与模型的尺寸比例定为20倍,主裂缝长度为200 m,高度为40 m,则对应的模型主裂缝长度为10 m,高度为2 m,裂缝的宽度与实际裂缝宽度保持一致,取6 mm,则得到的主裂缝尺寸为10 m×2 m×6 mm,然后设置次裂缝尺寸为10 m×2 m×3 mm;三级缝尺寸为5 m×2 m×3 mm。

复杂裂缝支撑剂实际模拟设置步骤如下。

(1)首先在数模软件的几何结构模块里在二维网格面上根据模型参数画出其二维视图,如图1所示。

(2)然后对其向上进行拉伸,可以获得三维立体模型,如图2所示。

图2 复杂裂缝三维立体模型图

(3)根据模型设计方案,设置模型的出入口、壁面等,然后使用结构化网格进行网格划分,单元尺寸为0.05 m,共计99 384个节点和48 440个单元,得到复杂裂缝网格划分图,如图3所示。

图3 复杂裂缝网格划分图

(4)以双精度模式打开fluent软件,选择其中的稠密离散相模型和瞬态计算选项,规定重力方向,检查网格是否存在问题,然后设置模型求解方法、壁面条件和模型中支撑剂及携砂液的各项参数,则可以得到完整的复杂裂缝缝网模型,如图4所示。

图4 复杂裂缝缝网模型图

考虑黏性力主导的动力相似条件,对应得到黏性力相似准数Re,对应表达式为

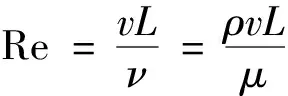
(9)

为满足相似条件,需Ren=Rem,m代表实际数据,n代表模型,可以得到模型速度表达式[22]为

(10)

式(10)中:ρ为流体密度,kg/m3;v为速度,m/s;L为裂缝长度,m;μ为流体黏度,mPa·s。

设置矿场和模型的流体密度值相同,如果设置矿场与模型的流体黏度相等,则此时模型的流速为实际流速的20倍,实际流速为0.1 m/s时,对应的模型流速为2 m/s,模型流速较大,支撑剂在裂缝中不易沉降,砂堤达到平衡所需得时间较长,为了减少模拟时间,将实际与模型的流体黏度比设置为5,将实际黏度值设为1 mPa·s,则对应的模型流体黏度为0.2 mPa·s,此时对应的模型流速为0.4 m/s。将模型的入口边界条件设置为速度入口,裂缝出口均设置为压力出口条件,压力为大气压。

3 支撑剂运移规律及不同因素对支撑剂铺置的影响

3.1 支撑剂运移规律

利用表1的基础数据开展复杂裂缝中支撑剂运移规律研究。

表1 基础模型数据及对应矿场数据表

通过模拟得到裂缝内砂堤形成过程,如图5所示。由图5可知,支撑剂进入裂缝后在裂缝底部沉降形成小段砂堤,在缝口处几乎无支撑剂沉降,当携砂液流动到主、次缝的分支处后,支撑剂开始进入次级缝,随着注入时间增长,主裂缝在分支后也形成一段砂堤,与分支前的砂堤之间存在一段空白区域,次级缝同样形成小段砂堤。携砂液继续注入,主裂缝的两段砂堤连接起来,次级缝的砂堤面积增大,部分支撑剂开始进入三级缝,然后随着时间的增长,各级裂缝内的砂堤高度和长度均逐渐增大,直至不变。

图5 裂缝内砂堤形成过程图

注入初始阶段(模拟时间t=9 s)支撑剂随携砂液进入裂缝因重力作用会发生沉降,由于液体的携带作用,支撑剂未在缝口处形成沉积,而是在距离缝口一段长度处少量均匀地分布在裂缝底部。由于裂缝分支存在,当携砂液流动到分支处时(t=12 s)会发生分流,模型的分支角度为90°,携砂液不易进入,因此只有少部分携砂液会进入次级缝,其余液体会继续在主裂缝中流动,由于携砂液分流,进入次级缝的流体流速会减小,流体的携带能力减弱,因此支撑剂进入次级缝后会较快沉降,在次级缝缝口产生堆积。裂缝分支后主裂缝中的携砂液流量减小,流速改变,分支处等效于一个“新的缝口”,与注入初始阶段相同,支撑剂会在距离“新的缝口”一段距离产生堆积(t=15 s),此时主裂缝中存在两段砂堤,两段砂堤间存在一段空白区域。

随着注入量的增大,主裂缝分支前的砂堤高度增大,会对注入的携砂液产生阻挡作用,携砂液对分支后空白区域的冲刷能力减弱,空白区域有支撑剂开始沉降,分支前后主裂缝砂堤连接起来(t=24 s)。注入量继续增大,支撑剂在主裂缝里形成明显堆积,裂缝中的砂堤长度和高度持续增加,由于尺寸原因,砂堤长度最远延展到出口,砂堤高度的增加导致上方过流断面面积减小,流速增大,当砂堤顶部支撑剂的沉降和流体冲蚀带走的支撑剂达到平衡时,砂堤的高度不再改变,整个砂堤达到平衡状态(t=90 s)。

由于次级缝中支撑剂在缝口处便开始堆积,所以次级缝中缝口处的砂堤高度最高,随携砂液的持续注入,次级缝中支撑剂的沉积在高度和长度上都得到延展,经过一段时间后,次缝内砂堤也达到平衡状态。次级缝的砂堤延展到一定程度后(t为53 s时),支撑剂开始进入三级缝,三级缝与次级缝的关系与主次裂缝的关系类似,铺置规律与次级缝也类似。

3.2 不同因素对有效支撑面积的影响

本文实验方案主要考虑注入速度、流体黏度、砂比、支撑剂粒径及密度等因素对支撑剂运移和铺置的影响。参考矿场数据,将相关数值设定在合理的范围内。在研究裂缝中砂堤的铺置时一般选用砂堤的长度、高度、二维面积等因素进行分析,由于本文中所有裂缝中砂堤长度均达到裂缝出口,研究裂缝长度没有意义,为了定量地探究相关因素对支撑剂铺置情况的影响,选用各级裂缝中砂堤的无因次面积(裂缝内砂堤二维面积/裂缝的二维面积)作为衡量标准,同时以砂堤铺置的均匀程度作为辅助标准进行分析。

3.2.1 注入速度

选择注入速度为0.1、0.2、0.4、0.6、0.8 m/s,其余参数与表1中的基础数据保持一致,模拟不同注入速度对支撑剂运移的影响,铺置情况及支撑面积如图6和图7所示。

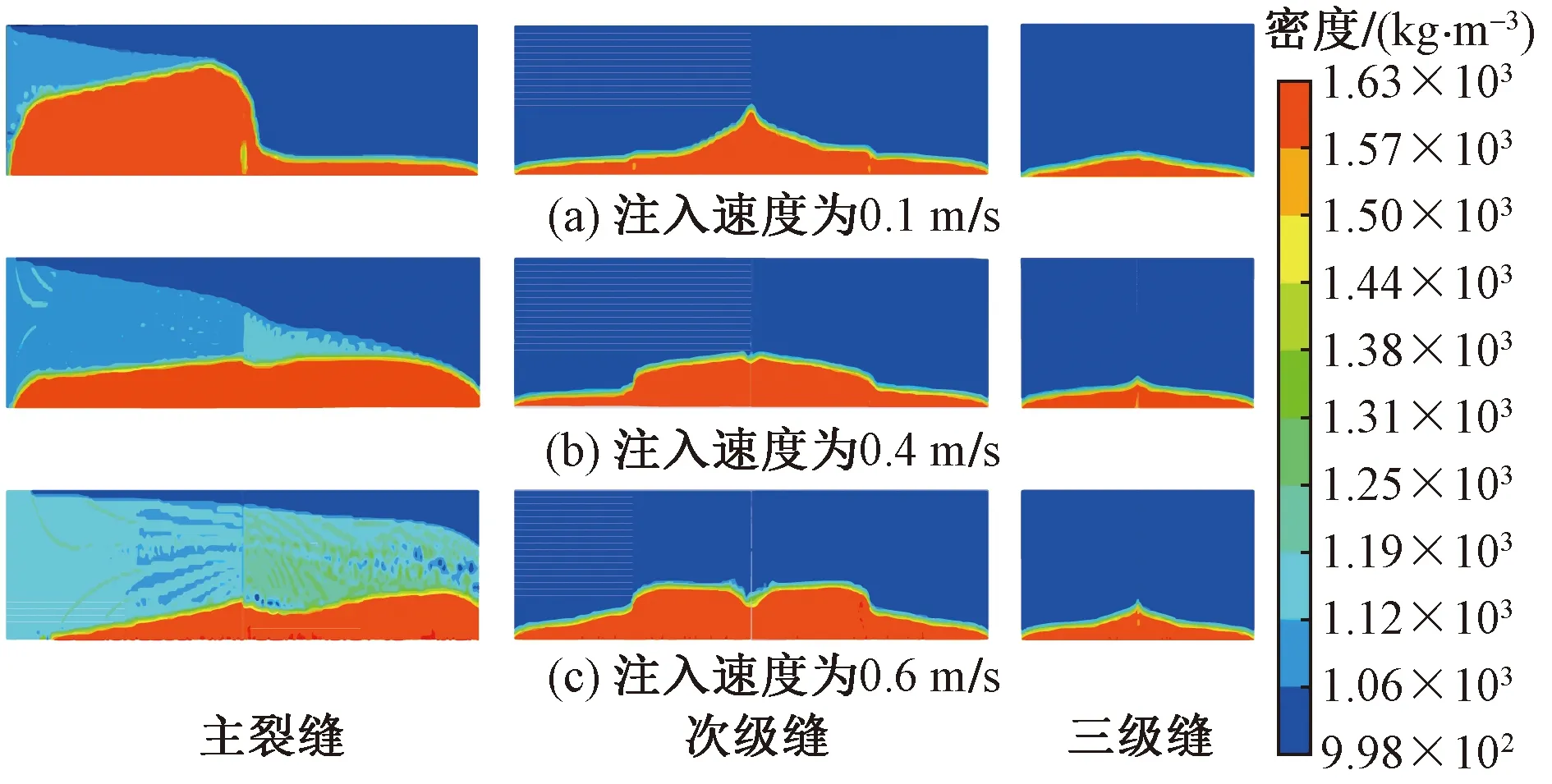
图6 不同注入速度下支撑剂铺置情况

图7 不同注入速度下各级裂缝中砂堤面积变化

如图6所示,随着注入速度的增大,主裂缝的砂堤高度是逐渐减小的,当注入速度较小时(0.1 m/s),主裂缝分支前的砂堤高度较高,接近缝高,分支后的砂堤高度较低,整体的均匀程度较差,不利用支撑剂发挥支撑裂缝的作用;当注入速度较大时(0.6 m/s),支撑剂更多地悬浮在流体中,主裂缝中的悬砂浓度较大,主裂缝的缝口处无砂堤形成,整体的砂堤高度较小,同样不利于支撑剂发挥支撑作用。次级缝的砂堤高度先减小后增大,均匀程度先变好后变差;三级缝均匀程度变差。

如图7所示,注入速度对支撑剂在裂缝内的铺置影响较大,主缝内随着注入速度的增大,砂堤的面积是逐渐减小的,次级缝的砂堤面积先增大后减小,三级缝内的砂堤面积处于波动状态,整体变化幅度较小。

注入速度较小(0.1 m/s)时,流体对支撑剂的携带能力差,支撑剂水平方向上的运移距离较短,在主裂缝入口的附近便较多地沉降,在裂缝分支前形成高度接近缝高的砂堤,导致砂堤上方的流动空间减小,导致通过的流体流速增大,支撑剂更多地被运移到出口,较少进入次级缝,分支后的砂堤高度较低,因此整体的铺置效果较差。流体流速增大(0.4 m/s)时,流体对支撑剂的携带能力增强,携砂液可以携带支撑剂到达各级裂缝,不再在入口处形成大量沉积,能够在主裂缝中形成均匀的砂堤,进入次级缝的支撑剂增多,所以主裂缝的砂堤面积减小,次级缝和三级缝的砂堤面积增大。注入速度较大(0.6 m/s)时,流体携带能力过强,支撑剂无法在主裂缝缝口沉降,即缝口处不能形成有效砂堤,停注后由于地应力作用会出现缝口闭合问题,变成无效裂缝,而且过强的携带能力会将大量的支撑剂悬浮在流体中,并携带到出口处,导致整个主裂缝的砂堤高度降低,砂堤面积减小,无法形成有效支撑,此时支撑剂的碰撞会更加剧烈,克服角度问题进入次级缝的支撑剂变多,因此次级缝砂堤面积增大;三级缝经过两次分支的作用,砂堤面积受到注入速度变化的影响较小。为了达到有效支撑的目的,流体速度的取值范围应该介于0.1～0.6 m/s。

3.2.2 流体黏度

按照前文相似原理的参数设定,选用0.5、1、2、4 mPa·s,其余参数与基础数据保持一致,来研究流体黏度对支撑剂运移的影响,铺置情况及支撑面积如图8和图9所示。

图8 不同流体黏度下支撑剂铺置情况

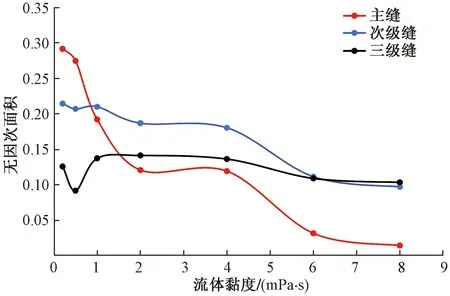
图9 不同流体黏度下各级裂缝中砂堤面积变化

如图8所示,随着流体黏度的增大,主裂缝中的砂堤长度和高度都是减小的,砂堤的均匀程度也是逐渐变差的,次裂缝砂堤高度逐渐减小,砂堤长度基本不变,砂堤的均匀程度逐渐增大,砂堤高度明显降低;三级缝的砂堤高度逐渐增大,长度和均匀程度变化不明显。

如图9所示,液体黏度对各级裂缝砂堤面积的影响程度逐渐减弱的,对主裂缝影响最大,对三级缝影响最小。液体黏度越大,支撑剂受到的浮力越大,支撑剂更容易悬浮在液体中,沉降速度越慢,支撑剂越容易被带出裂缝,因此裂缝中支撑剂的沉降越少,主次缝中的砂堤面积也越小。黏度越大,支撑剂受到的水平拖拽力也越大,支撑剂能更多地被带到出口,所以主次缝内的支撑剂沉降会减小,砂堤面积也随之减小。

3.2.3 砂比

矿场施工中砂比的浓度一般在10%左右,不超过20%。本文研究选用砂比5%、10%、15%、20%、25%,其余参数与基础数据保持一致,来研究砂比对支撑剂运移的影响,支撑面积变化如图10所示。

图10 不同砂比下各级裂缝中砂堤面积变化

随着砂比的增大,主裂缝的砂堤高度逐渐增大,砂堤长度和均匀程度变化不明显;次级缝的砂堤高度逐渐增大,砂堤的均匀程度因砂堤高度的增大而逐渐变差;三级缝砂堤的形态变化较小。

如图10所示,砂比对裂缝内砂堤面积的影响较大,在5%～20%范围内,主次裂缝的砂堤面积随着砂比的增大而增大,三级缝的砂堤面积变化不明显。当砂比从20%增大到25%时,主裂缝砂堤面积基本无变化,次裂缝砂堤面积继续增大,三级缝的砂堤面积也明显增大。

随着砂比的增大,携砂液会携带更多的支撑剂进入裂缝,同等条件下发生沉降的支撑剂颗粒增加,而且高砂比压裂液中支撑剂间的相互作用也会更加剧烈,会导致支撑剂更容易发生沉降,因此随着砂比的增大,各级裂缝的砂堤高度均增大,由于裂缝分支的存在和裂缝宽度的差别,进入三级缝的流体及支撑剂较少,砂比对三级缝砂堤面积的影响并不明显。当支撑剂浓度增大到20%后,支撑剂在裂缝的前端发生明显沉降,形成了大量沉积,主缝的砂堤高度较高,砂堤上部的流体通道较小,流体的流速会较大幅度增大,几乎全部的支撑剂都被运移到分支裂缝和主缝出口,因此尽管砂比增大了5%,但主缝的砂堤面积并没有发生明显变化,而次级缝和三级缝的面积明显增大。从砂比为25%的裂缝云图可以看到,砂堤高度已经达到裂缝高度的50%,再继续增大砂比,可能会出现砂堵的情况。考虑到施工条件和经济因素,压裂过程中砂比并不是越大越好,15%～20%是比较合适的取值范围,不能超过25%。

3.2.4 支撑剂粒径

压裂施工用到的支撑剂有不同大小的粒径,以矿场常用支撑剂的尺寸为研究对象,将支撑剂粒径设定在20/40目～60/90目范围内,其余参数与基础数据保持一致,来研究砂比对支撑剂运移的影响,支撑面积变化如图11所示。

图11 不同支撑剂粒径下各级裂缝中砂堤面积变化

随着支撑剂粒径增大,主、次缝内的砂堤高度均增大,均匀程度均逐渐变差;三级缝的砂堤形态基本不受影响。如图11所示,随着支撑剂粒径的增大,主缝内砂堤面积逐渐增大,当颗粒尺寸大于 0.4 mm 后,增大趋势变缓;次级缝的砂堤面积先增大后减小,在粒径为0.35 mm时,次级缝的砂堤面积达到最大;三级缝砂堤面积变化较小。

支撑剂粒径越大,主缝内的砂堤二维面积越大,这是因为主裂缝的宽度远大于颗粒尺寸,流体及颗粒在其中的流动相对简单,粒径越大的支撑剂受到的重力也越大,也更容易发生沉降。压裂液从主缝流入次级缝时,由于液体分流及缝宽的变化导致流体的流动较为复杂,粒径较小的支撑剂容易被流体携带走,不易发生沉降形成砂堤;支撑剂粒径增大,发生沉降的支撑剂总量增加,砂堤面积增大;当粒径过大时,支撑剂沉降较快,在次级缝的缝口便开始堆积,堆积特点是先在砂堤高度上进行堆积,形成一定高度后,砂堤上部的流动空间减小,压裂液的流速增大,对大粒径支撑剂的携带能力加强,能够将支撑剂更多地带离缝口,甚至到达出口处,缝口的堆积高度较大时会导致支撑剂整体铺置效果变差,次级缝的砂堤面积会相应地减小,所以次级缝存在最大砂堤面积。当支撑剂粒径较小时,进入裂缝的支撑剂主要在主、次裂缝内沉积或通过主次缝的出口流出裂缝,少部分会在三级缝内沉降;支撑剂尺寸增大时,由于三级缝的缝宽较小,支撑剂不易进入,所以仍是少部分支撑剂在三级缝中沉降,因此三级缝的砂堤面积变化幅度较小,粒径变化对其产生的影响比较轻微。

3.2.5 支撑剂密度

将支撑剂密度设定在1 600～2 800 kg/m3范围内,其余参数与基础数据保持一致,来研究砂比对支撑剂运移的影响,支撑面积变化如图12所示。

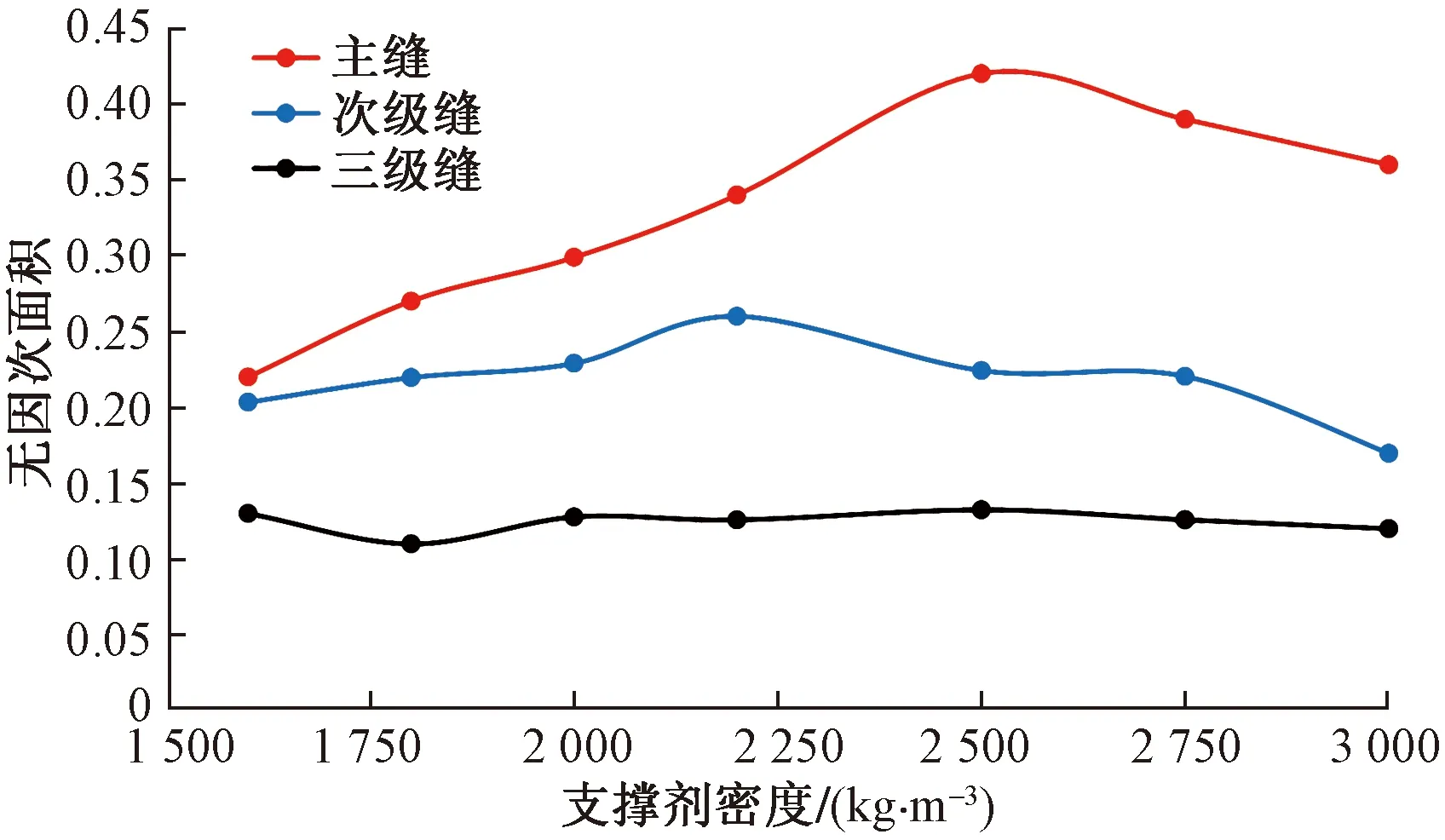
图12 不同支撑剂密度下各级裂缝中砂堤面积变化

随着支撑剂密度的增大,主裂缝中悬砂面积减小,主、次缝砂堤高度均逐渐增大,均匀程度逐渐变差;三级缝的砂堤高度在小范围内波动,均匀程度变化不明显。如图12所示,随着支撑剂密度的增大,主、次裂缝砂堤面积均表现为先增大后减小的特征;三级缝砂堤面积变化幅度较小。

当密度较小时,支撑剂更多地悬浮在液体中,随着支撑剂密度的增大,支撑剂受到的重力增大,更多的支撑剂发生沉降,主次缝中砂堤面积增大。当支撑剂密度增大到2 500 kg/m3时,主缝中的砂堤面积达到最大。支撑剂密度继续增大,此时由于密度较大,支撑剂在到达裂缝分支处前便产生大量沉积,砂堤高度接近缝高,砂堤上部的流动空间较小,流体经过时流速增大,携带能力增强,将更多的支撑剂带离裂缝,因此主缝在裂缝分支后的铺置情况较差,主裂缝砂堤面积减小;较多的支撑剂从主缝出口离开裂缝,且次级缝缝口砂堤高度也较高,所以次级缝砂堤面积也会减小,即次裂缝砂堤面积与分支前主缝的高度有关,所以让次级缝达到最大砂堤面积的支撑剂密度应小于主缝砂堤最大面积对应的支撑剂密度。密度的改变对裂缝内支撑剂运移的影响主要表现在主、次裂缝中,三级缝砂堤面积变化较小。

4 裂缝内有效支撑面积预测模型及验证

由于模型的网格数、支撑剂数目较多,导致任意一组参数进行计算耗时均较长,如利用3.1节研究复杂裂缝铺置过程时的对应参数进行计算,模拟至砂堤稳定所需时长为7～8 h。

为了节省计算时间,本文研究提出了裂缝内有效支撑面积预测模型,利用数值模拟方法得到支撑面积数据样本,并用于BP神经网络模型训练,然后利用非训练数据进行结果准确性分析。选用主裂缝的砂堤面积进行训练,这是由于主裂缝内的支撑剂铺置受注入速度等因素的影响较大,砂堤面积变化较大,在数值上的分布范围更广,若主裂缝支撑面积预测结果良好,则说明次级缝和三级缝的砂堤面积可以用相同的方法进行预测。

4.1 BP神经网络

4.1.1 神经网络简介

BP神经网络是一种多层前馈网络,不需要建立数学表达式,对输入的样本数据学习训练,获得隐藏在数据内部的规律,并利用学习到的规律来预测未来的数据。它的网络结构包含输入层、隐含层和输出层,如图13所示。学习过程包括输入信息的正向传递和误差信息的反向传递,以实际的输出值和期望输出值之间的均方误差为判断依据,调整神经网络的权值和阈值,最终使均方误差达到预期[23]。

xm为输入层的输入数据;yn为输出层的输出数据

4.1.2 构建神经网络

以注入速度、流体黏度、砂比、粒径及密度作为神经网络的输入变量,以主裂缝中砂堤面积作为输出结果。通过数值模拟一共得到了45组数据样本,其中32组数据样本用于训练集,8组数据样本用于验证集,剩下的5组数据样本用于检验模型的预测性能。输入数据的数值相差几个数量级,为了避免出现训练时间长,收敛慢或误差较大的情况,需要将数据进行归一化,映射到(0,1)区间内。

输入层神经元个数与输入数据的维数相同,输出层神经元个数与需要拟合的数据个数相同,隐含层神经元个数与层数需要根据一些规则和目标来设定[24-25],本文使用的神经网络是3层网络。

在神经网络中隐含层节点数的选择非常重要,不仅对建立的神经网络模型的性能影响很大,而且是训练中出现过拟合的直接原因,但目前理论上还没有一种较为准确的隐含层节点数确定方法。只能以经验公式来确定大概范围,计算公式为

(11)

式(11)中:A为隐含层节点数;M、N分别为输入层、输出层的节点数。

隐含层节点数在A值的附近时,均方误差较小。为了获得最好的训练结果,通过试错法来得到隐含层的节点数,发现隐含层节点数为3时,拟合的相关度较大,均方误差较小。因此构建神经网络模型的输入层、隐含层和输出层节点数分别为5、3、1,其结构为5-3-1。

4.2 神经网络预测性能

4.2.1 模型的训练效果

在神经网络模型进行预测前,需要对模型进行训练,利用前文得到的实际数据进行训练,得到网络模型训练完成后的权重,如表2所示。

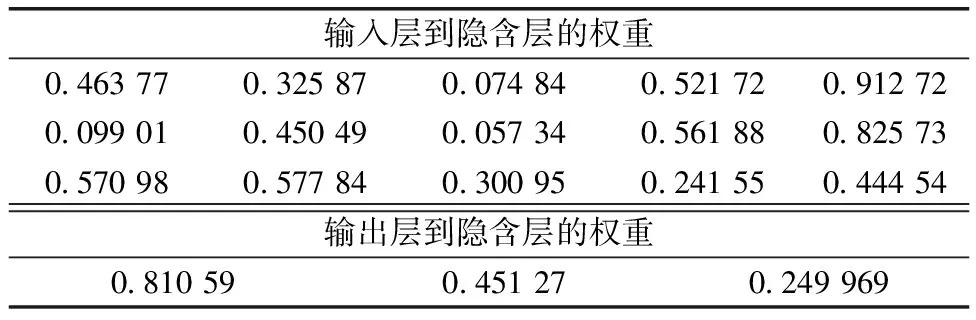
表2 训练完成后的各级权重

如表2所示,对应的输入层到隐含层的阈值为0.982 063、0.578 268、0.234 423,输出层到隐含层的阈值为0.955 438。

图14和图15为神经网络模型的预测值与实际结果的关系图,该模型的神经网络模型训练集的预测值和试验值的相关系数为0.989 18,验证集的预测值和试验值的相关系数为0.974 46,均接近1,数据均匀地分布在直线y=x的两侧,说明训练效果良好。

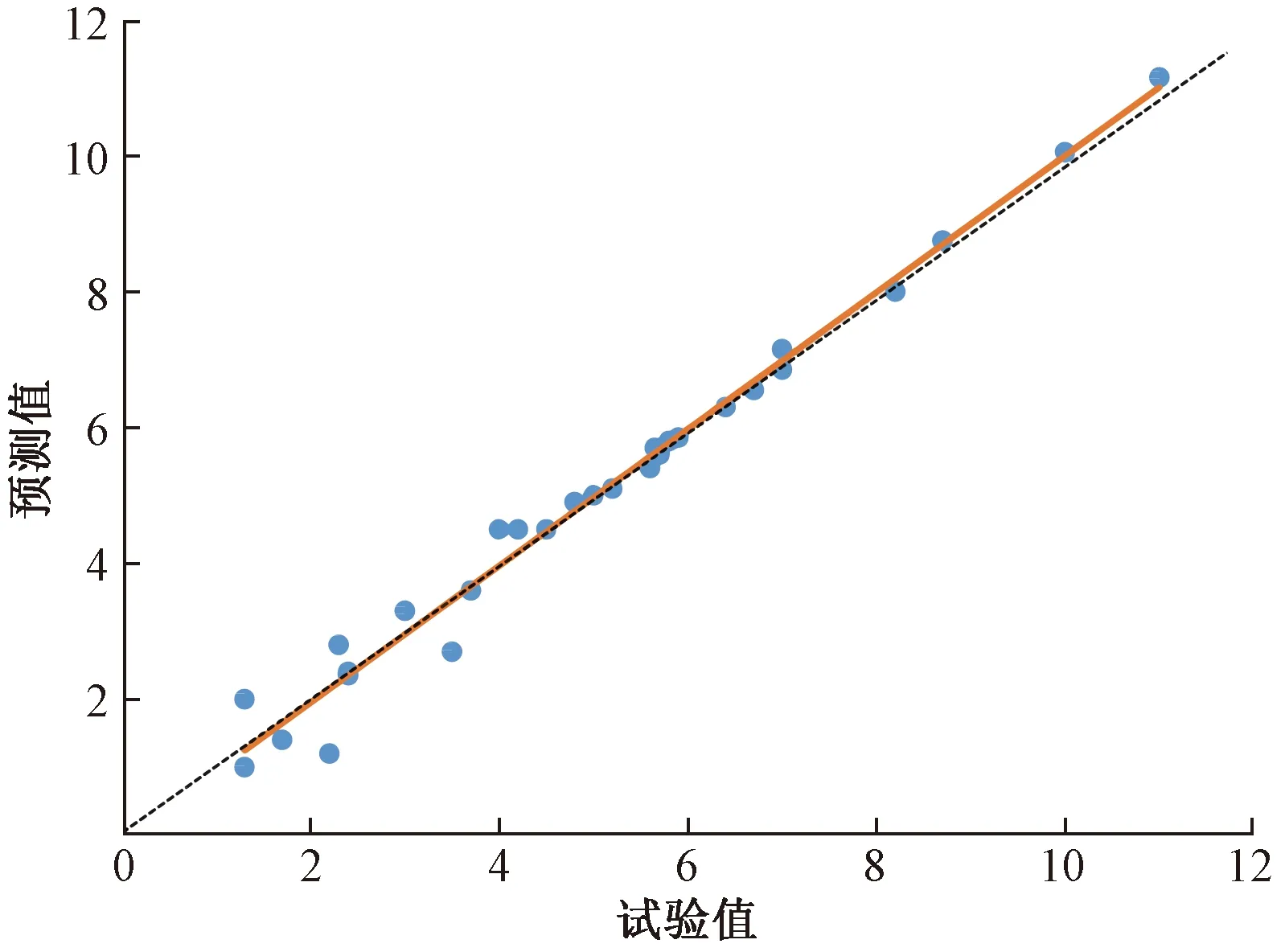
图14 训练集预测值与试验值的相关性

图15 测试集预测值与试验值的相关性

4.2.2 模型预测结果验证

利用训练好的神经网络模型对测试集的数据进行模拟预测,选取5组不同的参数,分别标号为 A～E,进行5次预测取平均值,避免结果误差较大,具体数据如表3所示。

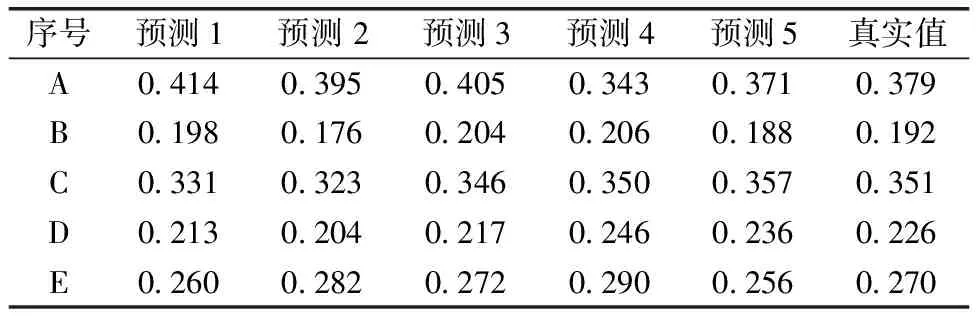
表3 神经网络预测值与实际值对比表

如表3所示,计算得到对应的平均误差分别为6.35%、5.46%、3.42%、6.46%、4.28%。每组参数预测结果的误差均不超过10%,处于5%左右,说明构建的BP神经网络对支撑剂在裂缝中砂堤面积的预测结果良好,可以用来较快速且相对准确地得到裂缝中砂堤面积的大小,并进行参数优化及寻找最优方案,具有一定的实用价值。

从结果及验证可以看出,利用主缝的实验数据对模型进行训练后,再利用模型进行主缝有效支撑面积预测,得到了较为准确的预测结果,说明这种预测方法是可行的。如果想要预测次级缝和三级缝的砂堤面积,同样可以利用各自对应的实验数据进行模型训练,然后进行结果预测。

5 结论

(1)携砂液流动到分支处时发生分流,少部分携砂液会进入次级缝并在缝口产生堆积,对于主裂缝后半段,分支处等效一个“新的入口”。当砂堤顶部支撑剂的沉降量和流体冲蚀带走的支撑剂达到平衡时,则砂堤达到平衡状态。

(2)注入速度增大,主缝砂堤面积逐渐减小,次级缝砂堤面积先增大后减小,速度较大或较小时,铺置效果均较差。流体黏度越大,各级裂缝中的砂堤面积越小。砂比增大,主、次裂缝的砂堤面积增大,当砂比超过17%后,主缝砂堤面积趋于稳定,三级缝的砂堤面积明显增大。支撑剂粒径增大,主缝砂堤面积逐渐增大,粒径超过0.4 mm后增大趋势变缓,次裂缝砂堤面积在粒径为0.35 mm时达到最大砂堤面积。支撑剂密度增大,主、次裂缝的砂堤面积均先增大后减小,最大砂堤面积分别在密度为2 500、2 200 kg/m3时出现。

(3)分支前主缝的砂堤高度较高时,裂缝分支后的次级缝的铺置效果会变差,因此主、次缝的最大砂堤面积不会同时出现。次级缝与三级缝的铺置关系与主次裂缝的关系类似。

(4)建立了基于BP神经网络的裂缝内有效支撑面积预测模型,模型预测结果与数值计算结果误差在3.42%～6.46%,该模型能够准确、快速地预测支撑剂在裂缝中运移后形成的砂堤面积。